
대수와 그래프를 이용한 벡터의 덧셈
출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)
Video
벡터 a와 벡터 b 2차원 벡터 두 개가 있습니다. 벡터 a와 벡터 b의 합을 어떻게 정의할 수 있을지 한번 생각해 봅시다. 여러분이 처음 떠올린 생각은 아마도 둘 다 두 값을 가진 2차원 벡터이니 대응하는 값을 서로 더하는 것일 겁니다. 벡터의 합의 첫 번째 값을 여기 두 벡터의 첫 번째 값의 합으로 채우고 6 + (- 4) = 2 입니다. 그리고 벡터의 합의 두 번째 값을 두 벡터의 두 번째 값의 합으로 채웁니다 - 2 + 4 = 2가 나오네요. 2차원 벡터 두 개의 합도 2차원 벡터임을 보았습니다. 실수 좌표 공간에서 생각해 보면 둘 다 \(R^{2}\)의 벡터 입니다.
벡터 a와 벡터 b 둘 다 \(R^{2}\) 의 벡터 입니다. 둘 다 2-튜플이라는 뜻이죠. 둘 다 2차원 벡터라는 말입니다. 우리가 표기한 방법으로 보면 이해가 되지만 시각적으로 혹은 개념적으로 어떻게 이해해야 할까요? 이 벡터들을 그래프에 그려보면 알겠죠. 이 벡터들을 시각적으로 한번 표현해 보겠습니다.
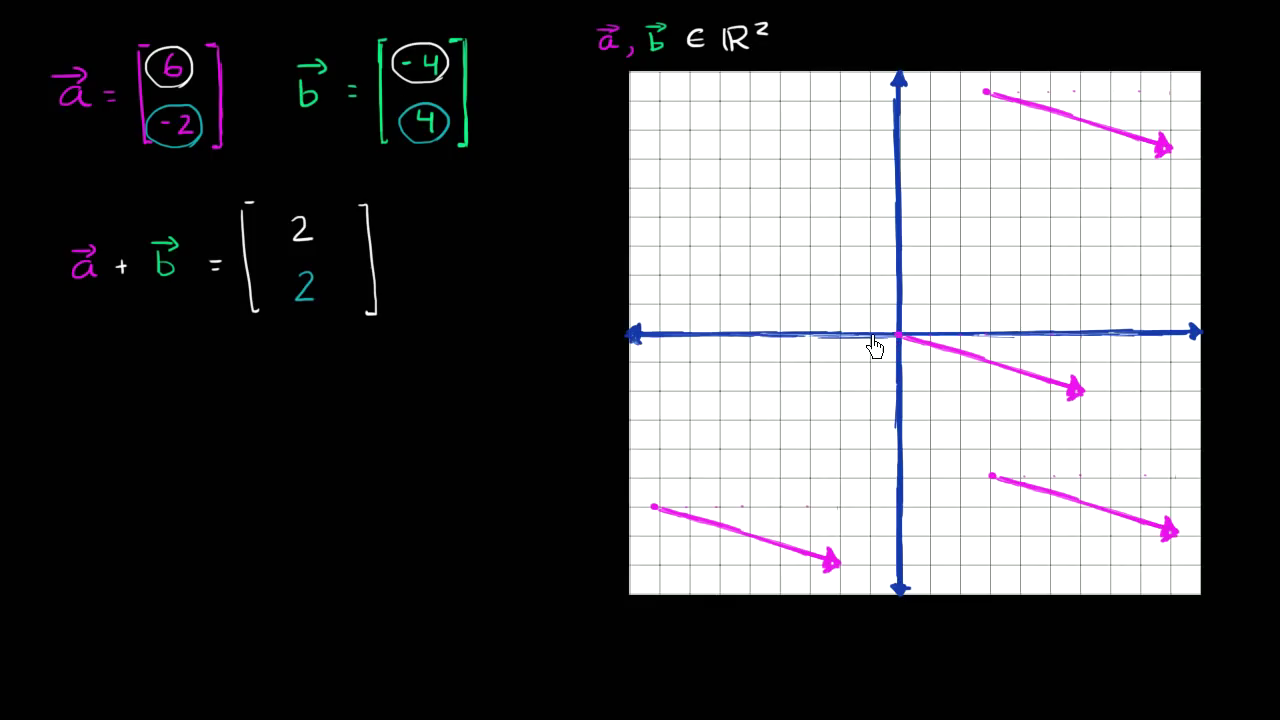
벡터 a를 봅시다. 이 값들은 벡터가 얼마만큼 이동하는지 알려줍니다.
수평과 수직, 각 방향으로 말이죠. 벡터의 꼬리를 원점에 두면 꼬리를 꼭 원점에 둘 필요는 없습니다만
편의를 위해서 원점에 두겠습니다.
수평으로 6칸 가고 수직으로 -2칸 갑니다. 벡터 a는 이렇게 생겼습니다.
다시 한 번 말하지만 중요한 것은 크기와 방향입니다.
크기는 벡터의 길이로 표현되고 방향은 벡터가 가리키는 방향을 말합니다. 꼭 강조하고 싶은 점은 벡터를 여기에 그릴 수도 있지만 다른 곳에 그려도 똑같은 벡터라는 점입니다. 다 같은 벡터 a입니다. 중요한 것은 오직 크기와 방향뿐입니다. 그 점을 명심하도록 합니다. 이번에는 벡터 b를 그려볼까요?
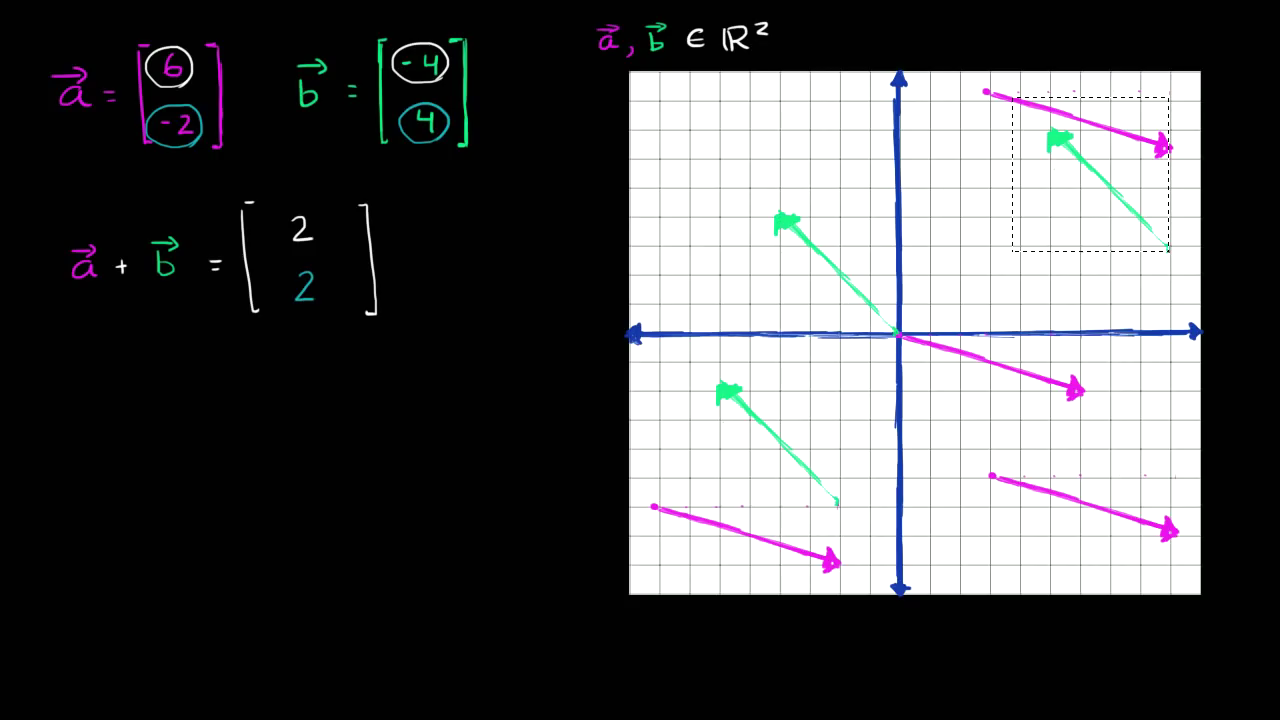
벡터 b는 수평 방향으로 - 4만큼 갑니다. 그리고 수직 방향으로 4만큼 갑니다. 만약 꼬리를 원점에 두었다면 머리는 (-4, 4)에 위치할 겁니다. 벡터 b를 여기에 그려보았습니다. 다시 한 번 말하지만 벡터 b를 이렇게 그릴 수도 있지만 복사 후 붙여넣기를 해볼게요. 이런 식으로도 벡터 b를 그릴 수 있습니다. 다시 한 번 말하지만 중요한 것은 오직 크기와 방향 뿐입니다. 여기 있는 녹색 벡터들은 크기가 다 같습니다. 길이가 다 같고 방향도 다 똑같습니다. 벡터 a와 벡터 b를 그린 방식이 합을 구하는 것과 어떤 연관이 있을까요? 둘의 합을 같은 방식으로 파란색으로 그려보겠습니다.
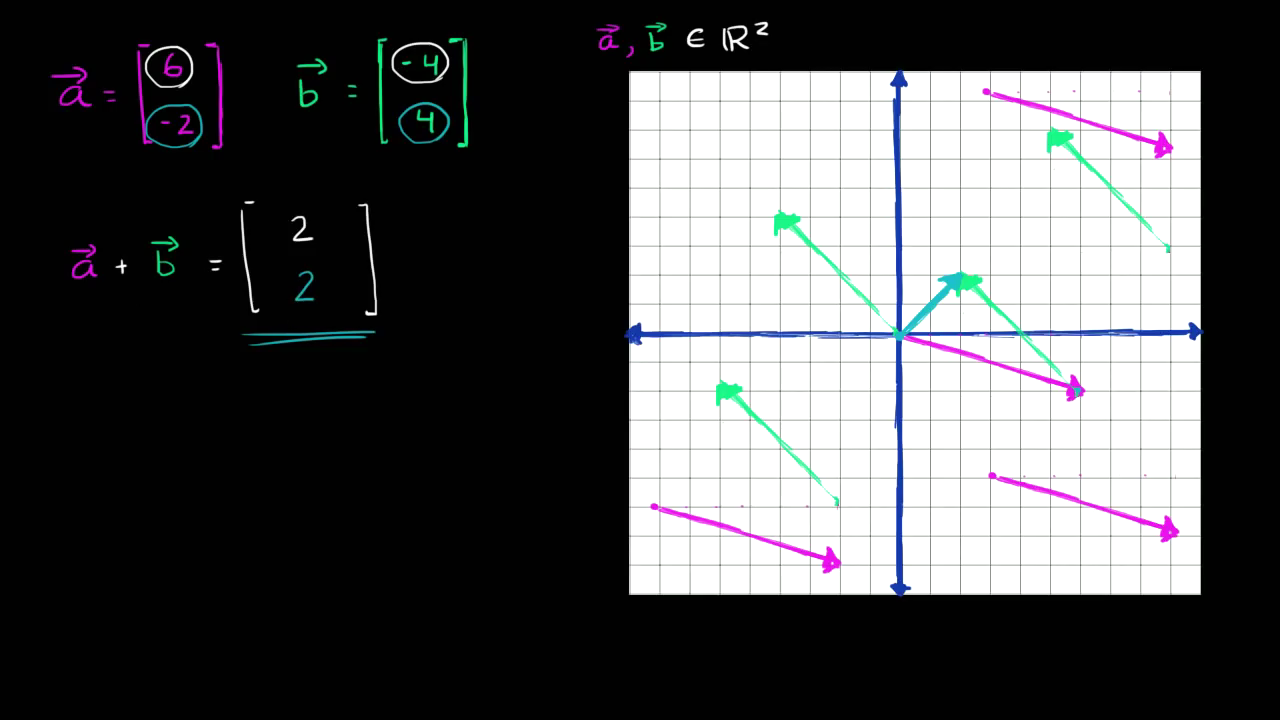
벡터의 합은 (2, 2) 이므로 이렇게 그릴 수 있습니다. 이것을 어떻게 이해해야 할까요? 보라색 벡터와 녹색 벡터를 더한 것이 이 파란색 벡터와 같다는 점을 말이죠. 벡터 a 더하기 벡터 b를 할 때 벡터 b의 꼬리를 벡터 a의 머리에 둡니다. 원점으로부터 얼마나 움직였나요? 다시 말하자면, 벡터는 이동뿐만 아니라 속도, 전기 가속 등등 여러 가지에 적용될 수 있으나 어떤 경우라도 이처럼 그래프에 그려보면 이해가 쉽습니다. 두 벡터의 합인 여기 파란색 벡터를 보세요. 벡터 a가 원점에서부터 이동한 곳에서 벡터 b의 꼬리를 여기에 두면 벡터합인 파란색 벡터의 머리까지 이동하게 됩니다. 그러면 이런 의문점이 생길 수도 있습니다. 벡터 a 더하기 벡터 b가 이것이면, 벡터 b 더하기 벡터 a는 무엇일까요? 둘이 같을까요? 처음 벡터 합을 구했던 방식으로 대응하는 값을 더한다면 벡터의 합은 똑같을 겁니다. -4 + 6 은 2이고 4 + (- 2)도 2입니다. 하지만, 시각적으로도 일치할까요?
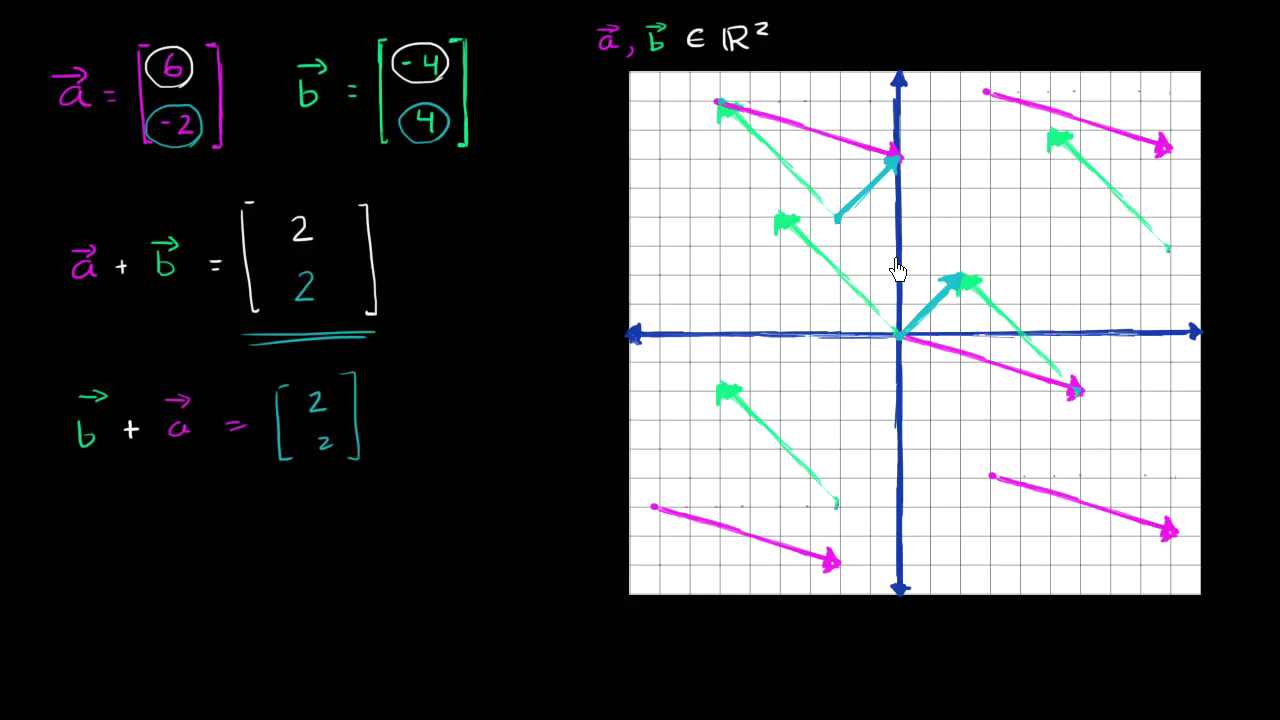
벡터 a의 꼬리를 벡터 b의 머리에 두면 생기는 파란색 벡터의 값이 무엇이죠? (2, 2)입니다. 수평으로 2 만큼, 수직으로 2 만큼 이동한다고 볼 수 있습니다. 더하는 순서를 바꿔도 결과는 같습니다. 시각적으로도 개념적으로도 이해가 되었길 바랍니다.
