최적화 이론 기초 정리 (Gradient Descent, Newton Method, Gauss-Newton, Levenberg-Marquardt 등)

Calculus 관련 글 목차

• 사전 지식 필요 : 최소제곱법
• 사전 지식 필요 : Gradient, Jacobian, Hessian 개념
• 참조 : https://people.duke.edu/~hpgavin/ExperimentalSystems/lm.pdf
• 참조 : https://towardsdatascience.com/bfgs-in-a-nutshell-an-introduction-to-quasi-newton-methods-21b0e13ee504
• 참조 : https://youtu.be/C6DCtQjKkdY

• 이번 글에서는 최적화 기법을 이용할 때, 가장 기본적으로 사용되는 기법들에 대하여 다루어 보려고 합니다. 본 글에서 다룬 내용은 최적화 기법의 가장 기초적인 내용이며 풀고자 하는 문제에 맞게 각 기법들을 적용하여 사용하시면 됩니다.
• 본 글을 읽기 전에 위에 명시되어 있는 최소제곱법과 Gradient, Jacobian, Hessian 개념 개념 숙지가 필요한 점 참조 부탁 드립니다.

목차

• Gradient Descent

• SGD

• Momentum

• RMSProp

• Adam

• Newton Method

• Quadratic approximation

• Newton Method for Optimization

• Gauss-Newton Method for Non-Linear Least Squares

• Levenberg-Marquardt Method for Non-Linear Least Squares

• Weighted Residuals

• Quasi Newton Method for Non-Linear Least Squares

• Lagrange Multiplier

Gradient Descent

SGD

Momentum

RMSProp

Adam

Newton Method

• 참조 : https://gaussian37.github.io/math-mfml-intro_to_optimisation/#newton-raphson-method-1

Quadratic approximation

Newton Method for Optimization

• 앞에서 배운 newton method에서는 \(f(x) = 0\) 의 해를 찾기 위하여 다음과 같이 식을 정의 후 iteration을 통하여 \(f(x) = 0\) 를 만족하는 해를 점진적으로 찾아 갔습니다.

• \[x_{i+1} = x_{i} - \frac{f(x_{i})}{f'(x_{i})}\]

• 문제의 관점을 조금 바꾸어서 단순히 \(f(x) = 0\) 의 \(f(x)\) 가 임의의 다항식이 아니라 Objective Function이라고 가정해 보겠습니다. 물론 Objective Function 또한 앞에서 정의한 다항식과 동일하게 표현될 수 있지만 의미상으로 정답 \(y_{i}\) 와 예측값 \(\hat{y}_{i}\) 간의 차이를 정의한 함수라고 생각해 보겠습니다.
• 이번에 다룰 예제 함수는 다음과 같은 함수입니다.

• \[y = a \cdot e^{-wt}\]

• 위 식에서 \(a\) 는 상수이고 구하고자 하는 파라미터는 \(w\) 입니다. \(t\) 가 입력값이고 \(y\) 가 출력값입니다.
• 위 함수식을 이용하여 Objective Function을 SSE(Sum of Square Error) 형태로 아래와 같이 정의하겠습니다. 사용되는 데이터의 갯수는 \(n\) 개로 이번 글에서는 8개의 데이터 샘플을 사용할 예정입니다.

• \[\text{SSE} = \sum_{i=1}^{n}(y_{i} - \hat{y}_{i})^{2} = \sum_{i=1}^{n}(y_{i} - a e^{-wt_{i}})\]

• SSE는 convex function으로 아래로 볼록한 형태를 가지게 됩니다. 따라서 critical point (임계점)을 찾기 위해 SSE의 1차 미분이 0이되는 지점을 찾는 문제로 변환하여 풀 수 있습니다.
• newton metehod를 이용하여 이 문제를 접근한다면 다음과 같이 식을 정의할 수 있습니다.

• \[w_{\text{new}} = w_{\text{old}} - \frac{f'(w_{\text{old}})}{f''(w_{\text{old}})}\]
• \[\text{SSE} = \sum_{i} (y_{i} - a e^{-wt_{i}})\]
• \[\frac{\partial \text{SSE}}{\partial w} = \sum_{i=1}^{n}2(y_{i} - ae^{-wt_{i}}) \cdot t_{i}ae^{-wt_{i}}\]
• \[\frac{\partial^{2} \text{SSE}}{\partial w^{2}} = \sum_{i=1}^{n} -2y_{i}t_{i}t_{i}a e^{-wt_{i}} - ((2ae^{-wt_{i}})(-t_{i}t_{i}ae^{-wt_{i}}) + (-2t_{i}ae^{-wt_{i}})(t_{i}ae^{-wt_{i}}))\]

• 위 식들을 이용하여 newton method를 적용하면 다음과 같습니다.

• \[w_{\text{new}} = w_{\text{old}} - \frac{\left(\frac{\partial \text{SSE}}{\partial w}\right)}{\left(\frac{\partial^{2}\text{SSE}}{\partial w^{2}}\right)}\]

• 단순히 1차 미분과 2차 미분을 이용하여 \(w_{\text{old}} \to w_{\text{new}}\) 로 업데이트 한다는 것에서 앞에서 살펴본 다차 방정식의 해를 구하는 것과 큰 차이는 없습니다.

• 이번에는 위 함수에서 상수 \(a\) 를 파라미터로 변경하여 다음과 같이 2개의 변수 \(w = (w_{1}, w_{2})\) 를 가지는 multivariable function으로 변경해 보도록 하겠습니다.
• 최종적으로 구하고자 하는 형태가 vector-valued multivariable function에서의 최적화이기 때문입니다.

• \[y = w_{1} \cdot e^{-w_{2}t}\]
• \[w_{\text{new}} = w_{\text{old}} - \frac{f'(w_{\text{old}})}{f''(w_{\text{old}})}\]
• \[\begin{bmatrix}w_{0(\text{new})} \\ w_{1(\text{new})} \end{bmatrix} = \begin{bmatrix} w_{0(\text{old})} \\ w_{1(\text{old})} \end{bmatrix} - H^{-1}G\]
• \[G (\text{Gradient}) = \begin{bmatrix} \frac{\partial f}{\partial w_{1}} \\ \frac{\partial f}{\partial w_{2}} \end{bmatrix} = \begin{bmatrix} e^{-w_{2}t} \\ -w_{1}te^{-w_{2}t} \end{bmatrix}\]
• \[H (\text{Hessian}) = \begin{bmatrix} \frac{\partial^{2}f}{\partial w_{1}^{2}} & \frac{\partial^{2}f}{\partial w_{1} \partial w_{2}} \\ \frac{\partial^{2}f}{\partial w_{2} \partial w_{1}} & \frac{\partial^{2}f}{\partial w_{2}^{2}} \end{bmatrix} = \begin{bmatrix} 0 & -t e^{-w_{2}t} \\ -t e^{-w_{2}t} & w_{1}t^{2}e^{-w_{2}t} \end{bmatrix}\]

• 위 식에서 \(H^{-1}\) 과 \(G\) 는 newton method에서 각각 아래 값과 대응됩니다.

• \[f'(w) = G\]
• \[\frac{1}{f''(w)} = H^{-1}\]

• 따라서 newton method를 이용하여 Objective Function을 최적화 할 때, 위 식을 통하여 점진적으로 해를 구할 수 있습니다.
• 위 식을 통하여 아래 데이터에 대하여 \(w_{1}, w_{2}\) 을 최적화 해보려고 합니다.

t = [0, 20, 40, 60, 80, 100, 120, 140]
y = [147.8, 78.3, 44.7, 29.5, 15.2, 7.8, 3.2, 3.9]

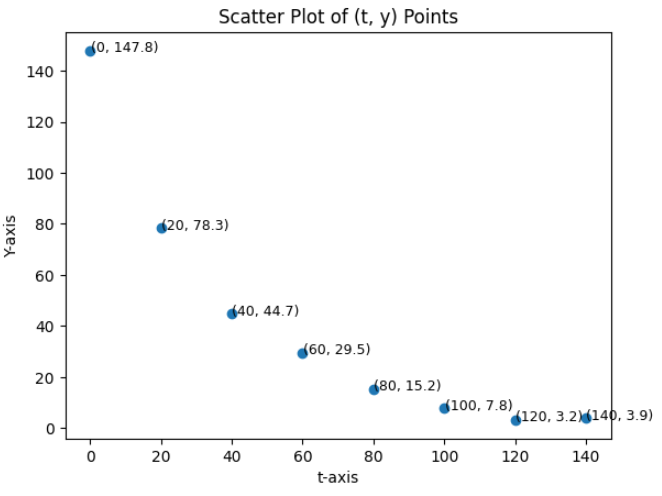
• 위 데이터는 총 8개의 쌍으로 다음과 같이 기호로 적을 수 있습니다.

• \[\begin{bmatrix} x_{0} & y_{0} \\ x_{1} & y_{1} \\ x_{2} & y_{2} \\ x_{3} & y_{3} \\ x_{4} & y_{4} \\ x_{5} & y_{5} \\ x_{6} & y_{6} \\ x_{7} & y_{7} \end{bmatrix} = \begin{bmatrix} 0 & 147.8 \\ 20 & 78.3 \\ 40 & 44.7 \\ 60 & 29.5 \\ 80 & 15.2 \\ 100 & 7.8 \\ 120 & 3.2 \\ 140 &3.9 \end{bmatrix}\]

• 그런데 newton method를 이용하여 최적화 하려고 하면 각 데이터에 대하여 Hessian을 구해야 하는 복잡함이 발생합니다. 따라서 각 행마다 다음과 같이 Hessian을 구하여 표현해 주어야 합니다.

• \[H_{0} = \begin{bmatrix} 0 & -(0) e^{-w_{2}(0)} \\ -(0) e^{-w_{2}(0)} & w_{1}(0)^{2}e^{-w_{2}(0)} \end{bmatrix}\]
• \[H_{1} = \begin{bmatrix} 0 & -(20) e^{-w_{2}(20)} \\ -(20) e^{-w_{2}(20)} & w_{1}(20)^{2}e^{-w_{2}(20)} \end{bmatrix}\]
• \[\vdots\]
• \[H_{7} = \begin{bmatrix} 0 & -(140) e^{-w_{2}(140)} \\ -(140) e^{-w_{2}(140)} & w_{1}(140)^{2}e^{-w_{2}(140)} \end{bmatrix}\]

• 예를 들어 least squares와 같은 경우에는 \(Ax = b\) 에서 \(x = (A^{T}A)^{-1}A^{T} b\) 와 같이 해를 구할 때, 모든 데이터 성분을 2차원 행렬 ( \((n, m)\) ) \(A\) 와 벡터 \(b\) 에 표현합니다.
• 하지만 newton method를 이용하여 최적해를 구할 때에는 Hessian으로 인하여 하나의 식으로 표현한다면 2차원 행렬인 Hessian을 행의 요소로 가지는 3차원 텐서로 표현해주어야 하는 복잡함이 발생합니다. (Hessian을 이용한 newton method의 출력은 matrix-valued multivariable function이 됩니다.) 그리고 2차 편미분에 대한 실제 계산도 복잡합니다.
• 따라서 newton method를 least squares와 같이 표현하여 계산 복잡도를 줄이는 방법이 필요합니다.

Gauss-Newton Method for Non-Linear Least Squares

• gauss-newton method는 optimization 문제를 풀 때, 2차 미분을 사용하는 Hessian 대신에 1차 미분을 사용하는 Gradient를 이용하여 근사해를 구하는 방식입니다. 이 때, Gradient를 \(n\) 개의 function에 대하여 (vector-valued multivariable function) 적용하므로 Jacobian을 이용하게 됩니다.
• Jacobian을 이용하여 gauss-newton method에서 표현하고자 하는 것은 least squares(최소제곱법)를 반복적(iterative)으로 적용하는 것입니다.
• 이 방식을 통해 linear function의 해를 구하는 least squares를 non-linear function의 해를 구하는 non-linear least squares로 표현하는 것이 gauss-newton method의 핵심이라고 말할 수 있습니다.
• linear function의 해는 least squares를 한번 적용하여 해 또는 근사해를 구할 수 있습니다. 반면 non-linear function의 해는 linear function에 사용되는 least suqares를 단 한번 적용해서 근사해를 바로 구하기 어렵기 때문에 반복적으로 적용하며 점근적으로 근사해를 찾아갑니다.

• 이번에는 newton method for optimization 부분에서 다룬 내용을 이어서 어떻게 gauss-newton method를 통해 non-linear least squares를 해결하는 지 살펴보도록 하겠습니다.

• \[y = w_{1} \cdot e^{-w_{2}t}\]
• \[\text{SSE} = \sum_{i}^{n} (y_{i} - w_{1} \cdot e^{-w_{2}t})^{2}\]
• \[\text{Let } r_{i} = (y_{i} - w_{1} \cdot e^{-w_{2}t}). \ \ r \text{: residual}\]
• \[\text{SSE} = \sum_{i=1}^{n} r_{i}^{2} = r^{t} r\]

• chain rule을 이용하여 편미분을 적용해 보도록 하겠습니다.

• \[\frac{\partial \text{SSE}}{\partial w_{j}} = 2 \sum_{i}^{n} r_{i} \cdot \frac{\partial r_{i}}{w_{j}} \to \sum_{i}^{n} r_{i} \cdot \frac{\partial r_{i}}{w_{j}}\]
• \[\because \text{Constant(2) are deleted. It does not affect parameter estimation.}\]

• 아래와 같이 함수의 곱의 미분법에 따라 \(\frac{\partial^{2} \text{SSE}}{\partial w_{j} \partial w_{k}}\) 를 정의할 수 있습니다.

• \[r(x) = f(x)g(x)\]
• \[r'(x) = f'(x)g(x) + f(x)g'(x)\]

• \[\frac{\partial^{2} \text{SSE}}{\partial w_{j} \partial w_{k}} = \sum_{i}^{n} \left( \frac{\partial r_{i}}{\partial w_{j}}\frac{\partial r_{i}}{\partial w_{k}} + r_{i}\frac{\partial^{2} r_{i}}{\partial w_{j}\partial w_{k}} \right)\]

• 여기까지는 앞에서 다룬 newton method와 동일합니다. 앞에서 제기한 newton method의 문제점인 표현 및 계산의 복잡성을 단순화하고 least squares의 구조를 가질 수 있도록 식을 변경하기 위해서는 \(\frac{\partial^{2} \text{SSE}}{\partial w_{j} \partial w_{k}}\) 를 아래와 같이 단순화 해야 합니다.

• \[\begin{align} \frac{\partial^{2} \text{SSE}}{\partial w_{j} \partial w_{k}} &= \sum_{i}^{n} \left( \frac{\partial r_{i}}{\partial w_{j}}\frac{\partial r_{i}}{\partial w_{k}} + \color{red}{r_{i}\frac{\partial^{2} r_{i}}{\partial w_{j}\partial w_{k}}} \right) \\ &\approx \sum_{i}^{n} \left( \frac{\partial r_{i}}{\partial w_{j}}\frac{\partial r_{i}}{\partial w_{k}} \right) = J_{r}^{T}J_{r} \end{align}\]

• 위 식의 빨간색 부분은 2차 미분으로 값이 매우 작아지기 때문에 생략하여도 결과에 큰 영향이 없다는 점과 빨간색 부분을 생략함으로써 파라미터 업데이트 부분을 least squares 형태로 나타낼 수 있다는 특징이 있습니다. 이 부분은 바로 뒤에서 살펴보도록 하겠습니다.
• 이와 같이 식을 정리함으로써 SSE의 1차 미분과 2차 미분의 결과는 다음과 같이 Jacobian으로 표현할 수 있습니다.

• \[\frac{\partial \text{SSE}}{\partial w_{j}} \approx \sum_{i}^{n} r_{i} \cdot \frac{\partial r_{i}}{w_{j}} = J_{r}^{T} r\]
• \[\frac{\partial^{2} \text{SSE}}{\partial w_{j} \partial w_{k}} \approx \sum_{i}^{n} \left( \frac{\partial r_{i}}{\partial w_{j}}\frac{\partial r_{i}}{\partial w_{k}} \right) = J_{r}^{T} J_{r}\]

• 위 결과값을 이용하면 newton method에서 사용하였던 \(G\) 와 \(H\) 는 다음과 같이 정의 됩니다.

• \[G = \frac{\partial \text{SSE}}{\partial w_{j}} \approx J_{r}^{T} r\]
• \[H = \frac{\partial^{2} \text{SSE}}{\partial w_{j} \partial w_{k}} \approx J_{r}^{T} J_{r}\]

• 따라서 newton method에서 사용하였던 파라미터 업데이트 수식을 다음과 같이 변경할 수 있습니다.

• \[\begin{align} \begin{bmatrix}w_{0(\text{new})} \\ w_{1(\text{new})} \end{bmatrix} &= \begin{bmatrix} w_{0(\text{old})} \\ w_{1(\text{old})} \end{bmatrix} - H^{-1}G \\ &= \begin{bmatrix} w_{0(\text{old})} \\ w_{1(\text{old})} \end{bmatrix} - (J_{r}^{T} J_{r})^{-1}J_{r}^{T} r \end{align}\]

• 앞에서 빨간색 식 부분을 생략하는 방식을 통해 Hessian을 근사화하여 위 식과 같이 나타내는 이유는 파라미터 업데이트를 least squares(최소제곱법) 방식을 이용하여 업데이트하기 위함입니다.
• 먼저 파라미터를 업데이트하는 \((J_{r}^{T} J_{r})^{-1}J_{r}^{T} r\) 부분은 최소제곱법에서 사용한 수식과 같습니다. 최소제곱법에서는 \(Ax = b\) 에서 \(x\) 의 해를 구할 때, \(x = (A^{T}A)^{-1}A^{T}b\) 와 같은 형식을 이용하여 해 또는 근사해를 구하였습니다.

• \[(A^{T}A)^{-1}A^{T}b \quad \text{ Vs. } \quad (J_{r}^{T} J_{r})^{-1}J_{r}^{T} r\]

• 앞에서 residual은 정답값과 파라미터를 통해 추정한 값 간의 오차인데 이 오차는 파라미터가 아직 업데이트가 완전히 되지 않아서 생긴 오차입니다. 따라서 residual은 업데이트해야 할 \(\Delta w\) 와 gradient의 곱으로 생긴 크기 만큼 발생합니다.

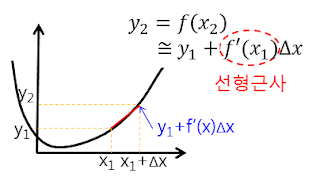
• 위 그림은 Jacobian을 설명하기 위한 참조 그림입니다. \(y_{2}\) 와 \(y_{1}\) 의 차이는 \(f'(x) \Delta x\) 만큼 차이가 나는 것으로 표현하였습니다.
• 이 때, \(\Delta x\) 는 앞에서 표현한 \(\Delta w\) 에 대응되고 \(f'(x)\) 는 gradient에 대응됩니다.
• 즉, \(y_{1}\) 을 추정값, \(y_{2}\) 를 정답값이라고 가정한다면 \(y_{1} \to y_{2}\) 로 근사화해 나아가는 것이 residual을 줄이는 것과 동일하게 생각할 수 있으므로 최적화 문제를 푸는 것이 됩니다.

• 이 때, 함수가 여러개이므로 residual의 gradient 대신에 Jacobian을 적용합니다. 따라서 \(J_{r} \Delta w = r\) 로 residual을 표현할 수 있습니다.
• 실제 구하고자 하는 값은 residual을 최소화하는 \(w\) 를 구하고 싶으므로 최적의 \(w\) 를 구하기 위한 \(w\) 의 변경량인 \(\Delta w\) 를 구하기 위하여 다음과 같이 least squares를 적용할 수 있습니다.

• \[J_{r} \Delta w = r\]
• \[\Delta w = (J_{r}^{T} J_{r})^{-1}J^{T} r\]

• 따라서 업데이트해야 할 \(\Delta w\) 를 구해서 \(w\) 에 반영하여 다음과 같이 \(w_{\text{old}} \to w_{\text{new}}\) 로 업데이트 하는 것이 문제를 해결하는 방법이 됩니다.

• \[w_{\text{new}} = w_{\text{old}} - (J_{r}^{T} J_{r})^{-1}J_{r}^{T} r\]

• 업데이트해야 할 \(\Delta w\) 를 least squares를 이용하여 구한 후 \(w\) 를 업데이트 하는데, 이 과정에서 한번의 least squares만을 이용하여 해를 구하지 않고 종료 조건이 만족될 때 까지 least squares를 반복하여 해 또는 근사해를 구하게 됩니다.
• 이와 같이 반복적인 근사화를 거치는 이유는 non-linear function에 least squares를 사용하기 때문입니다. (만약 linear function에서 least squares를 사용한다면 한번의 least squares를 적용할 수 있어서 별도 반복적인 근사화를 처지기 않습니다.)

• 지금까지 살펴본 예제는 파라미터가 \(w_{1}, w_{2}\) 2개이므로 Jacobian이 다음과 같이 정의 됩니다.

• \[\frac{\partial r_{i}}{\partial w_{1}} = -e^{-w_{2} t_{i}}\]
• \[\frac{\partial r_{i}}{\partial w_{2}} = t_{i}w_{1}e^{-w_{2} t_{i}}\]
• \[J_{r} = \begin{bmatrix} \frac{\partial r_{1}}{\partial w_{1}} & \frac{\partial r_{1}}{\partial w_{2}} \\ \frac{\partial r_{2}}{\partial w_{1}} & \frac{\partial r_{2}}{\partial w_{2}} \\ \vdots & \vdots \\ \frac{\partial r_{n}}{\partial w_{1}} & \frac{\partial r_{n}}{\partial w_{2}} \end{bmatrix} = \begin{bmatrix} -e^{-w_{2} t_{1}} & t_{1}w_{1}e^{-w_{2} t_{1}} \\ -e^{-w_{2} t_{2}} & t_{2}w_{1}e^{-w_{2} t_{2}} \\ \vdots & \vdots \\-e^{-w_{2} t_{3}} & t_{3}w_{1}e^{-w_{2} t_{3}} \end{bmatrix}\]

• 앞에서 이번 예제의 실제 데이터로 다음 데이터를 사용하기로 하였습니다. 따라서 아래 값을 대입해 줍니다.

t = [0, 20, 40, 60, 80, 100, 120, 140]
y = [147.8, 78.3, 44.7, 29.5, 15.2, 7.8, 3.2, 3.9]

• \[J_{r} = \begin{bmatrix} -e^{-w_{2} t_{1}} & t_{1}w_{1}e^{-w_{2} t_{1}} \\ -e^{-w_{2} t_{2}} & t_{2}w_{1}e^{-w_{2} t_{2}} \\ \vdots & \vdots \\-e^{-w_{2} t_{3}} & t_{3}w_{1}e^{-w_{2} t_{3}} \end{bmatrix} = \begin{bmatrix} -e^{-w_{2}(0)}=-1 & (0)w_{1}e^{-w_{2}(0)}=0 \\ -e^{-20 w_{2}} & 20 w_{1}e^{-20 w_{2}} \\ \vdots & \vdots \\ -e^{-140 w_{2}} & 140 w_{1}e^{-140 w_{2}} \end{bmatrix}\]

• 파이썬 코드를 통하여 Jacobian을 구하면 다음과 같습니다.

from sympy import symbols, Matrix, lambdify
import sympy as sp
import numpy as np
np.set_printoptions(suppress=True)

# Initial values (0, 0)
params = np.array([0, 0]).reshape(2, 1)
# Define symbolic variables for the parameters and points
w1, w2 = symbols('w1 w2')

t = [0, 20, 40, 60, 80, 100, 120, 140]
y = [147.8, 78.3, 44.7, 29.5, 15.2, 7.8, 3.2, 3.9]

# Define the residual function for a single point
residuals = Matrix([])
for t_i, y_i in zip(t, y):
    residuals = residuals.row_insert(residuals.shape[0], Matrix([y_i - w1 * sp.exp(-w2 * t_i)]))

residuals_func = lambdify([w1, w2], residuals, 'numpy')
r = residuals_func(params[0][0], params[1][0]) 

# Compute the Jacobian matrix of the residual function
jacobian = residuals.jacobian([w1, w2])

# Convert the Jacobian to a numerical function using lambdify
jacobian_func = lambdify([w1, w2], jacobian, 'numpy')

# Print the Jacobian matrix
Jr = jacobian_func(params[0][0], params[1][0])

• 위 코드에서 정의된 residuals의 결과는 다음과 같습니다.

• 위 코드에서 정의된 jacobian의 결과는 다음과 같습니다.

• residual_func와 jacobian_func를 이용하여 gauss-newton method를 다음과 같이 적용할 수 있습니다.
• max_iteration최대 반복 횟수이고 threshold는 이전 파라미터와 현재 업데이트한 파라미터 간의 차이가 있는 지 확인하기 위한 값입니다. 따라서 max_iteration을 초과하거나 threshold 이하의 업데이트 양이 발생하면 gauss-newton method를 종료합니다.

max_iteration = 30
threshold = 1e-7
prev_params = None
for i in range(max_iteration):
    # update parameters
    r = residuals_func(params[0][0], params[1][0])
    Jr = jacobian_func(params[0][0], params[1][0])
    update = np.linalg.pinv(Jr.T @ Jr) @ Jr.T @ r
    params -= update

    #### print out changes of parameters ###
    print("index:{}".format(i))
    if i > 0:
        print("prev_params: {}".format(prev_params.reshape(-1)))
    print("params:{}".format(params.reshape(-1)))
    print("update:{}\n".format(update.reshape(-1)))
    
    # check if updates are effective
    if i > 0:
        if np.sqrt(np.sum((prev_params - params)**2)) < threshold:
            break
            
    prev_params = params.copy()

# index:0
# params:[41.3  0. ]
# update:[-41.3   0. ]

# index:1
# prev_params: [41.3  0. ]
# params:[104.125        0.02173123]
# update:[-62.825       -0.02173123]

# index:2
# prev_params: [104.125        0.02173123]
# params:[145.08506266   0.02968753]
# update:[-40.96006266  -0.00795629]

# index:3
# prev_params: [145.08506266   0.02968753]
# params:[146.4444568    0.02918536]
# update:[-1.35939414  0.00050216]

# index:4
# prev_params: [146.4444568    0.02918536]
# params:[146.42476133   0.0291796 ]
# update:[0.01969547 0.00000577]

# index:5
# prev_params: [146.42476133   0.0291796 ]
# params:[146.42450411   0.0291794 ]
# update:[0.00025722 0.00000019]

# index:6
# prev_params: [146.42450411   0.0291794 ]
# params:[146.42449541   0.02917939]
# update:[0.0000087  0.00000001]

# index:7
# prev_params: [146.42449541   0.02917939]
# params:[146.42449511   0.02917939]
# update:[0.00000029 0.        ]

# index:8
# prev_params: [146.42449511   0.02917939]
# params:[146.4244951    0.02917939]
# update:[0.00000001 0.        ]

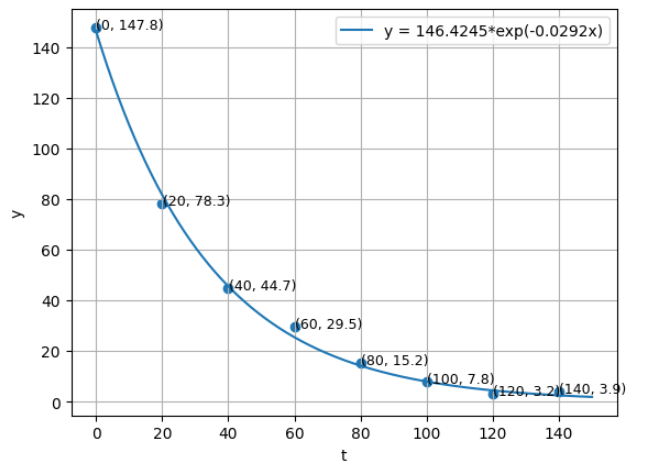
• 따라서 위 그래프와 같이 샘플 데이터를 잘 표현하는 함수 파라미터를 구할 수 있음을 확인하였습니다.

Levenberg-Marquardt Method for Non-Linear Least Squares

• 앞에서 다룬 gauss-newton method를 이용하여 non-linear least squares 문제를 해결하는 방법에서 다음 2가지 문제를 개선한 방법을 Levenberg-Marquardt Method라고 합니다.

Weighted Residuals

Quasi Newton Method for Non-Linear Least Squares

Lagrange Multiplier

Calculus 관련 글 목차