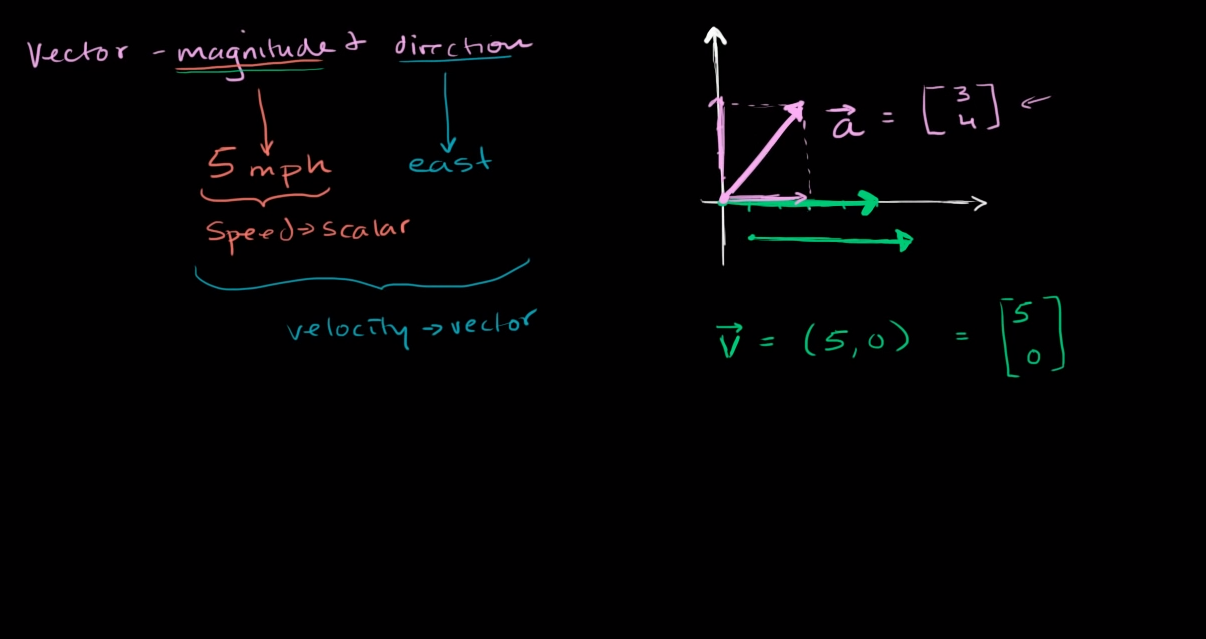
선형대수학을 위한 벡터란 ?
출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)
Video
벡터는 크기와 방향을 동시에 나타냅니다.
예를 들어벡터가 되는 것과 되지 못하는 것을 생각해 보죠.
어떤 물체가 시속 5마일로 움직인다고 합시다. 하지만 이 정보 자체는 벡터가 아닙니다.
단지 크기를 말합니다. 이 물체가 어느 방향으로 시속 5마일로 움직이는지 알 수 없죠.
속력이라고도 불리는 이 수치는 그 자체로는 벡터가 아닙니다. 이것은 스칼라입니다.
이 값이 벡터가 되기 위해서는 방향을 가져야합니다.
예를 들어 이 물체는시속 5마일의 속력으로 동쪽으로 움직이고 있다고 이야기할 수 있죠.
이제 시속 5마일로 와 동쪽으로라는 정보가 합쳐져서 벡터가 되었고 이 값을 더 이상 속력이라고 부르지 않습니다.
속도라고 부르죠. 즉, 속도는 벡터입니다.
이 정보를 시속 5마일로 동쪽으로 움직인다고 말할 수 있죠. 하지만, 어떻게 이 정보를 표현할 수 있을까요?
예를 들어 2차원에서 표현할 수 있죠. 선형대수가 진짜 멋진 이유는 2차원 뿐만 아니라, 3, 4, 5차원
6차원 이상으로 원하는 만큼 확장할 수 있고 3차원 너머서는 상상하기 어렵지만, 수학적으로는 3차원을 넘어서 다룰 수 있죠.
선형대수를 이용해서 말이죠. 그 내용은 나중에 배워보도록 하고 우선은 쉬운 2차원 벡터에서 생각합시다.
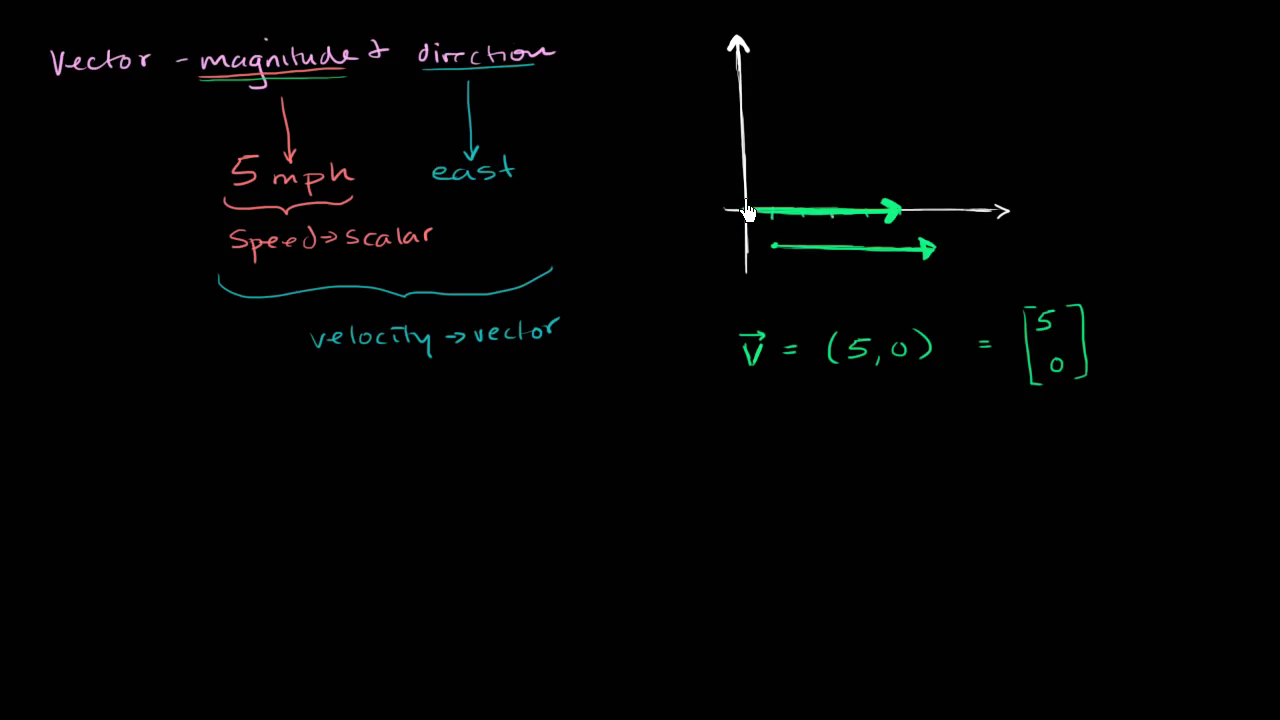
위 값을 2차원으로 표현하는 방법 중 하나는 5의 크기를 가지는 화살표를 그리는 것이죠.
여기 표현된 크기는 크기의 단위마다 시간당 속력을 나타냅니다. 그리고 방향은 오른쪽을 향합니다. 즉, 동쪽이죠.
그러면 예를 들어 여기서 시작해서, 오른쪽으로 길이가 5인 화살표를 그릴 수 있습니다. 여기서 화살표의 길이는 속력을 나타냅니다. 그리고 화살표가 가리키는 방향이 있습니다. 바로 여기 보이는 것이 벡터를 표현하였다고 볼 수 있습니다. x축이 동쪽을 가리킨다면, 다시 말해, x축 +방향으로의 움직임이 동쪽이라면 위로는 북쪽이고 밑으로는 남쪽이 됩니다. 그리고 벡터에서 재밌는 점은 크기와 방향만 신경쓰면 됩니다. 어디서 시작하는지 어디에 표현하는지 상관이 없습니다.
예를 들어 이것은 완전히 같은 벡터입니다. 이 벡터는 길이가 같아서 크기가 같고, 방향도 마찬가지로 동쪽을 향하고 있으니 같습니다. 따라서 이 두 벡터는 완전히 같은 벡터입니다
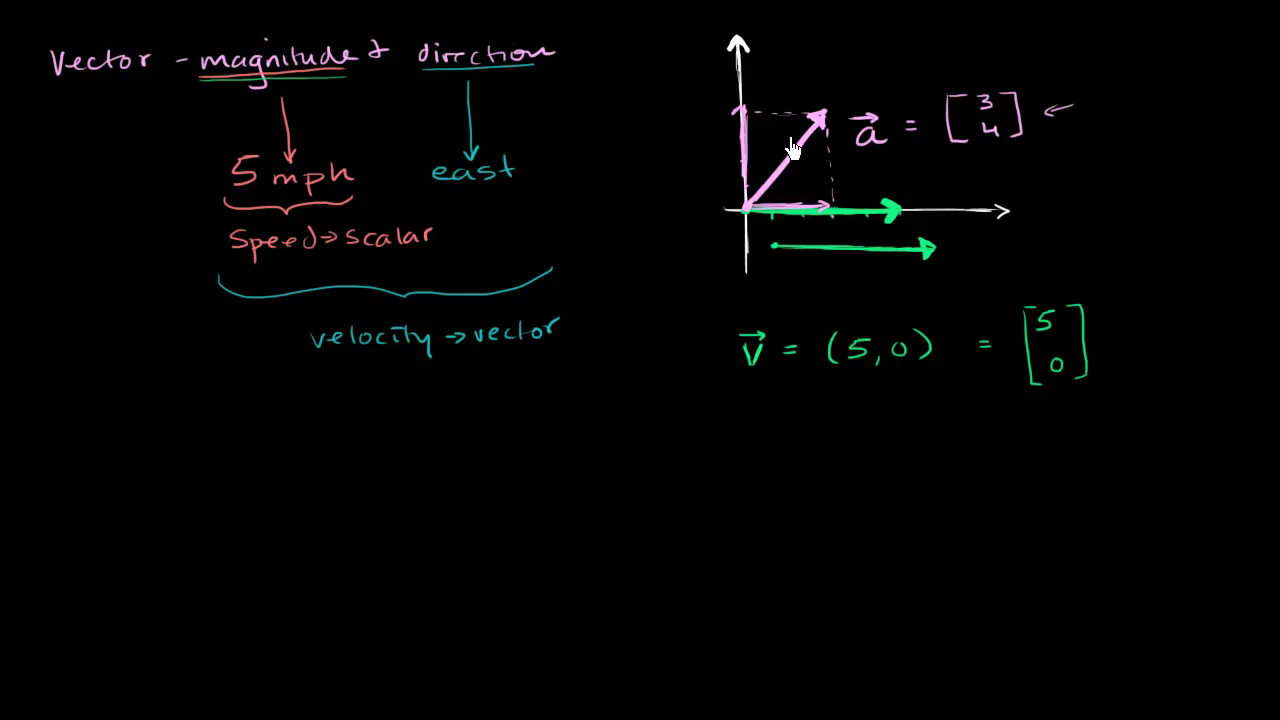
그럴듯 하지만 좀 더 수학적인 기호로 정교하게 표현할 수 없을까요? 매번 그림을 그릴 순 없어요. 이것으로 연산도 해볼수 있어야죠. 일반적으로는 벡터를 변수로 표현한다면 소문자를 사용해 표현합니다. 책에서는 굵은 글씨로 표현할 수 있지만 필기할 때에는 그냥 작은 화살표를 그 위에 그려주면 됩니다. 다양한 방법이 있을 수 있습니다. 예를 들면 동쪽으로 시속 5마일이라고 표현할 수 있겠지만 부정확하다는 느낌이 듭니다. 일반적으로 2차원이라면 숫자 2개로 벡터를 표현하는데 각 차원에 대해서 얼마만큼 움직였는지로 표현합니다. 예를 들어 이 물체는 오직 수평 축으로 움직였고 수평축을 먼저 표기하여 이렇게 표현할 수 있죠. (5, 0)은 수평축 +방향으로 5만큼 움직이며 수직축 방향으로는 전혀 움직이지 않는다는 걸 나타내죠. 다른 방식으로도 표현할 수 있습니다.
선형대수학에서는 일반적으로 열 벡터로 이렇게 표현하죠 [5 0], 다시 말하면 첫 번째 좌표는 수평으로 얼마나 움직였는지 나타내고 두 번째 좌표는 얼마나 수직으로 움직였는지를 나타냅니다.
다른 예로, 이런 벡터를 생각해 보죠. 수평으로 +3만큼 움직이고 수직으로 +4만큼 움직인 벡터가 있습니다. 이 벡터를 벡터 A라고 부르죠. 다시 한번 이 벡터를 표현한다면 이 벡터를 세분화해서 표현하면 수평으로는 +3만큼 움직였고 즉, +3만큼 수평 방향으로 움직였고 +4만큼 수직 방향으로 움직였네요. 즉, 화살표의 시작부터 끝까지 얼마나 위로 또는 얼마나 오른쪽으로 움직였는지 문자 그대로 표현됩니다. 화살표의 꼬리에서 시작해서 머리 방향으로 움직였을 때 말이죠. 그러므로 이 벡터는 [3 4]로 표현할 수 있습니다. 이제 피타고라스 정리를 사용해서 이 벡터의 길이를 구할 수 있어요. 이 삼각형은 3-4-5 삼각형이므로 그 크기는 5입니다.
그리고 선형대수학을 더 공부하게 되면 다양한 차원으도로 확장할 수 있습니다. 확실히 3차원까지는 시각화할 수 있지만 4차원부터는 좀 추상적입니다. 이렇게 차원이 높아지면 수학적으로 표현하는게 훨씬 낫죠. 4, 5, 혹은 20차원을 화살표로 그리기 힘드니까요.