헤딩 각(heading angle) 계산

2020, Feb 01    

Autonomous Driving 관련 글 목록

• 이번 글에서는 이미지에서의 자동차 헤딩 각을 알아보는 방법에 대하여 다루어 보도록 하겠습니다.
• 이미지의 자동차 헤딩 각이므로 2차원 평면임을 가정하고 다룹니다.

목차

• 헤딩각의 정의

• 벡터가 주어질 때, 그 벡터의 헤딩각

• 두 점이 주어질 때, 헤딩각

헤딩각의 정의

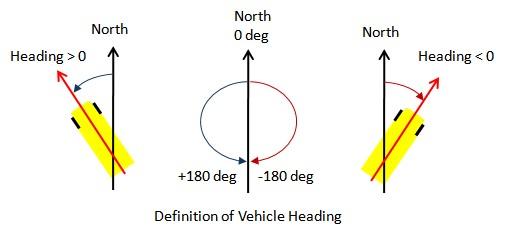
• 헤딩각은 북쪽을 기준점으로 하였을 때, 어떤 물체의 방향이 기준점인 북쪽과 얼만큼의 회전 각도를 가지고 있는 지를 의미합니다.
• 헤딩각은 0 ~ 180도의 영역과 -180 ~ 0도 까지의 영역으로 나뉩니다. 위 그림과 같이 0도는 정 북쪽 방향을 뜻하고 북쪽에서 반시계방향으로 이동하면서 + 각도가 되고 시계방향으로 이동하면서 - 방향이 됩니다.

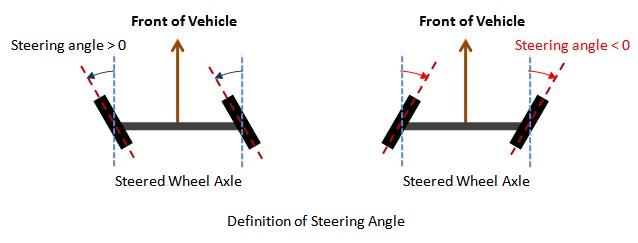
• 이 방향은 자동차에서 바퀴의 방향과 일치하므로 헤딩각은 스티어링각과 동일한 값을 갖습니다.
• 이 때, 정 북쪽이 실제로 북쪽을 나타내는 각도인 경우 내 자동차의 헤딩 각도 또한 위 기준으로 표현할 수 있습니다.

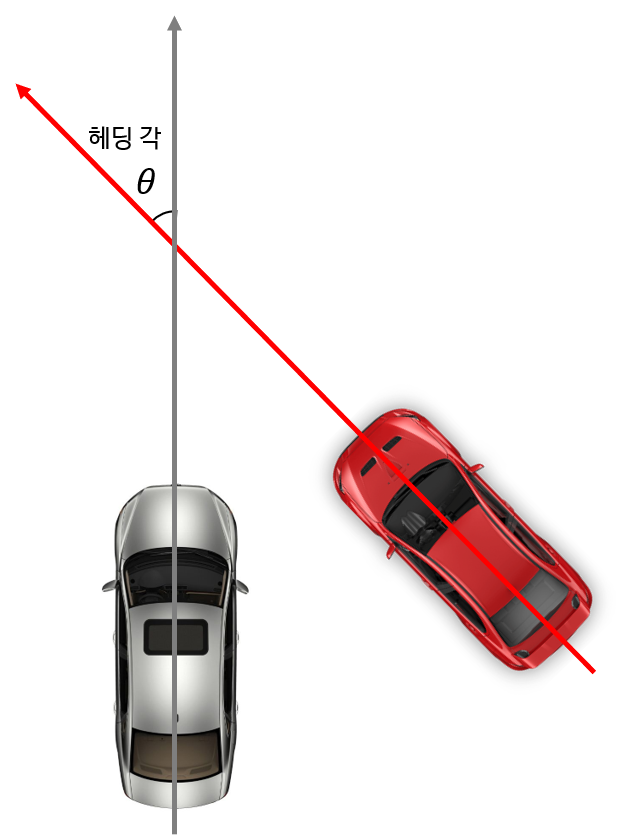
• 반면 나의 자동차를 절대 기준으로 잡고 내 자동차의 방향이 정 북쪽이라고 가정하면 나의 자동차를 기준으로 한 주위 자동차의 헤딩 각도를 표현할 수 있습니다.
• 위 그림과 같이 나의 자동차의 방향을 북쪽 이라고 하면 주위 자동차의 방향을 통하여 주위 자동차 들의 헤딩 각도를 구할 수 있습니다.

벡터가 주어질 때, 그 벡터의 헤딩각

• 어떤 벡터가 주어지면 벡터에는 방향이 있기 때문에 헤딩각을 쉽게 구할 수 있습니다.
• 두 벡터가 주어질 때, 벡터 사이의 각도를 구할 때에는 벡터의 외적을 이용하면 쉽게 구할 수 있습니다.

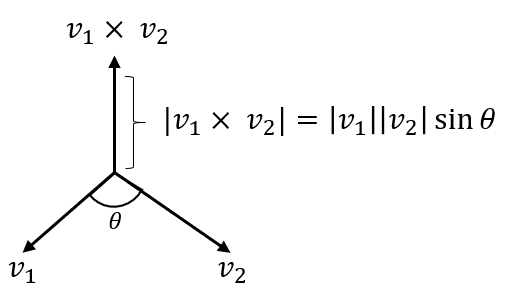
• 먼저 위 그림과 같이 두 벡터 \(v_{1}\)과 \(v_{2}\)가 있을 때, 두 벡터의 외적의 방향은 두 벡터가 이루는 2차원 평면에 직교합니다.
• 그리고 외적의 크기는 위 그림과 같이 \(\vert v_{1} \times v_{2} \vert = \vert v_{1} \vert \vert v_{2} \vert \text{sin}\theta\) 를 따릅니다.
  • 위 식이 도출되는 과정은 다음 링크를 참조하시기 바랍니다.
• 그러면 2차원 평면에서 두 벡터의 사이각은 위 식의 \(sin\theta\)를 이용하여 구할 수 있습니다.
• 벡터의 외적의 경우 교환 법칙이 성립하지 않고 교환하였을 경우 벡터의 방향이 바뀌게 되므로 방향에 민감합니다. 위 식에서 \(\theta\)는 \(v_{1}\) 벡터를 기준으로 \(v_{2}\)가 어느 방향으로 얼만큼 회전되어 있는 지를 나타냅니다.

• \[\theta = \text{sin}^{-1} \frac{ \vert v_{1} \times v_{2} \vert }{\vert v_{1} \vert \vert v_{2} \vert}\]

• 이 때, \(v_{1} = (x_{1}, y_{1})\) 이고 \(v_{2} = (x_{2}, y_{2})\) 이면 앞의 식에 그대로 대입할 수 있습니다.
• 벡터의 외적은 3차원 이지만 현재 2차원을 다루므로 z축의 값을 0으로 둔 것과 동일하다고 볼 수 있습니다.
• z축의 값을 0으로 두면 외적을 구할 때 z축과 연산되는 값은 모두 소거되므로 아래와 같이 구할 수 있습니다.

• \[\theta = \text{sin}^{-1} \Bigl( \frac{ x_{1}y_{2} - y_{1}x_{2} }{ \sqrt{x_{1}^{2} + y_{1}^{2}} \sqrt{x_{2}^{2} + y_{2}^{2}} } \Bigr)\]

• 여기서 \(\theta\)의 값이 양수이면 반시계 방향이고 음수이면 시계 방향입니다. 그리고 이 \(\theta\)의 값은 radian이므로 \(180 / \pi\)를 곱해주면 degree 값을 구할 수 있습니다.

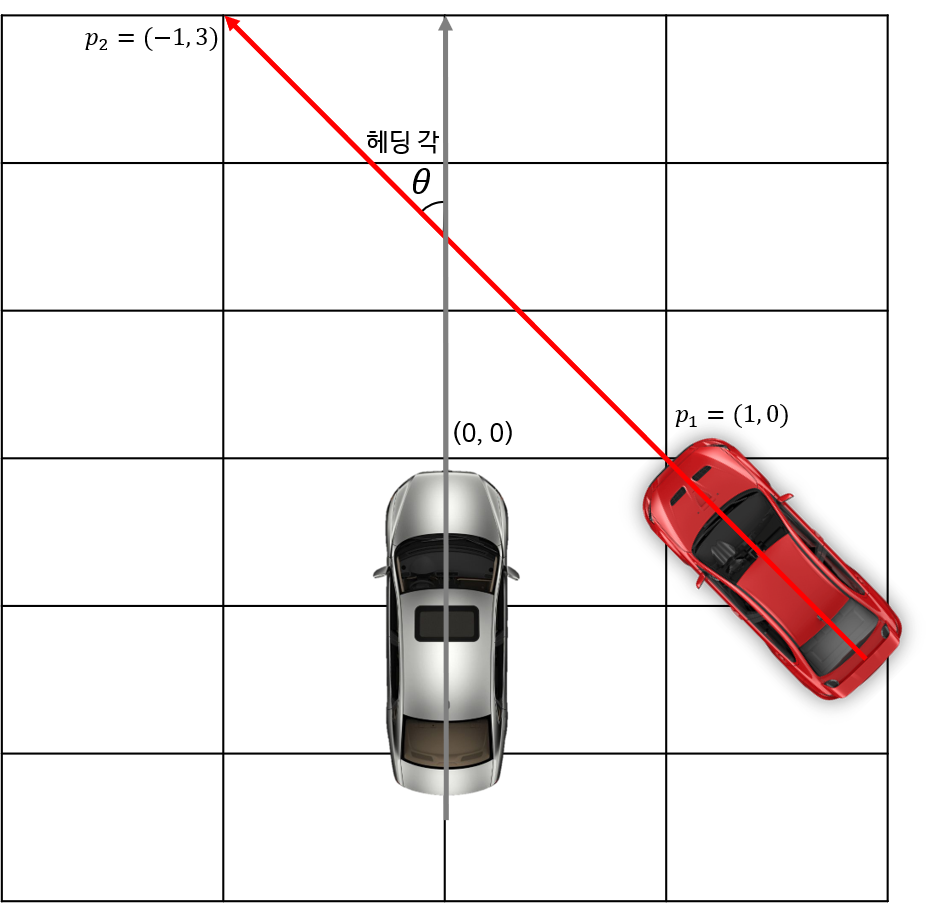
• 위 그림에서 회색 차를 기준으로 빨간색 차의 헤딩각을 구해보겠습니다.
• 여기서 기준이 되는 \(v_{1} = (0, 1)\)의 벡터로 잡을 수 있습니다. 현재 구하려고 하는 값이 각도이니 벡터의 크기는 계산이 편하게 잡겠습니다.
• 그러면 빨간색 차의 방향은 \(p_{1}\)을 시작점 \(p_{2}\)를 끝점으로 하는 벡터를 가지고 이 벡터는 \(v_{2} = p_{2} - p_{1} = (-2, 3)\) 이 됩니다.
• 위에서 정한 \(v_{1}, v_{2}\)를 이용하여 각도를 구하면 \(\theta = \text{sin}^{-1}(4 / \sqrt{13}) \approx 0.588\)이고 약 33.69도 가 됩니다.

두 점이 주어질 때, 헤딩각

• 두 점을 이용하여 헤딩각을 구할 때 발생할 수 있는 경우는 다음과 같습니다. (나의 차의 방향이 \(v_{1}\)이 된다는 기준입니다.)
• 여기서 주어진 두 점은 단순히 좌표 2개이며 방향은 없는 상태입니다.

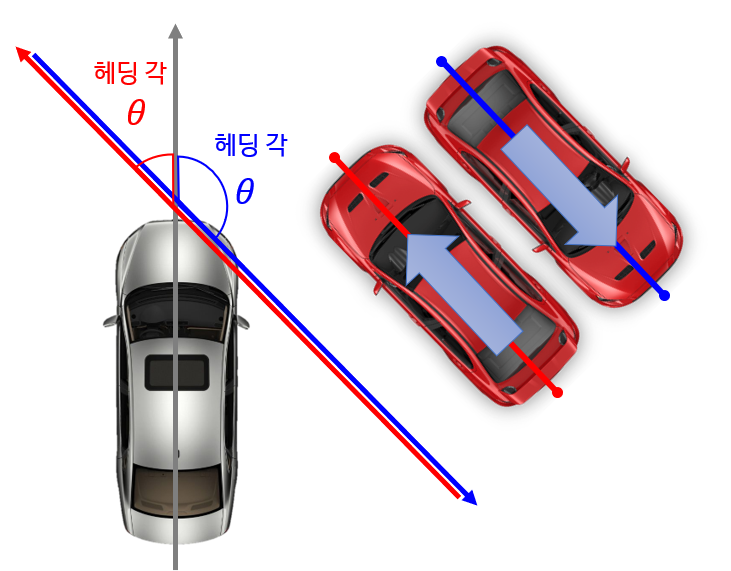
• 위와 같은 경우에는 \(p_{1} - p_{2}\)와 \(p_{2} - p_{1}\) 두 방향의 벡터를 구하고 두 방향의 벡터를 모두 구한 다음 상황에 맞추어 사용하면 됩니다.
• 물론 나의 차와 동일한 방향으로 간다는 가정이 있으면 두 점을 통하여 벡터를 구할 수 있으니 앞에서 다룬 방법대로 구하면 됩니다.
• 이번엔 응용을 해보겠습니다. 만약 다음과 같이 두 점이 주어지면 어떨까요?

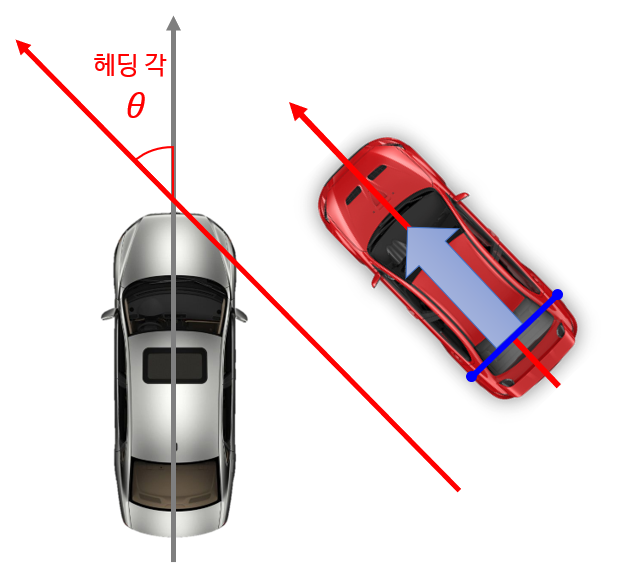
• 위 그림과 같이 차의 엣지를 이용하여 양쪽 끝 두 점을 얻었다고 가정하고 그 두점을 이용하여 헤딩각을 얻는다고 가정해 보겠습니다.

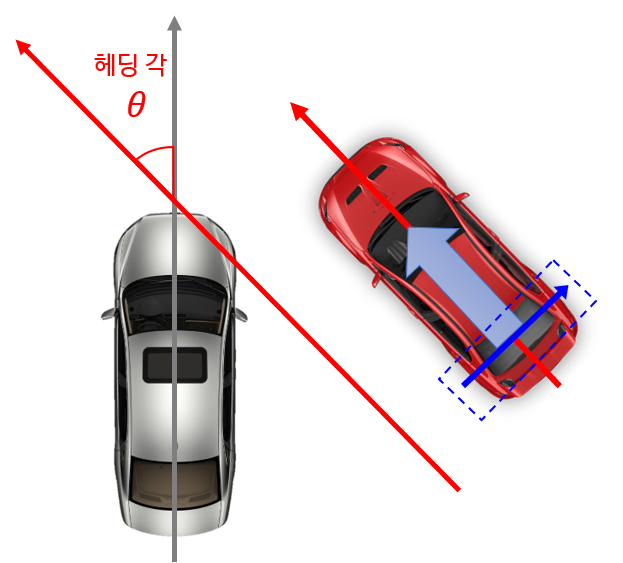
• 앞에서 다룬 것과 같이 방향이 없으면 빨간색 차의 방향은 두가지로 정할 수 있습니다.
• 위 그림과 같이 임의로 파란색 점을 있는 방향을 정해 보도록 하겠습니다. (왼쪽 바퀴 → 오른쪽 바퀴)
• 왼쪽 바퀴의 점을 \(p_{l}\) 라고 하고 오른쪽 바퀴의 점을 \(p_{r}\) 라고 하면 위 그림의 파란색 벡터는 \(p_{r} - p_{l}\)이 됩니다.
• 이 벡터를 90도 또는 -90도로 회전해 보도록 하겠습니다. 벡터의 회전 변환은 직교 행렬을 통하여 쉽게 변환할 수 있습니다.
  • 회변 변환에 대해서는 다음 링크를 참조하시기 바랍니다.
  • 링크 : https://gaussian37.github.io/math-la-rotation_matrix/

• \[\begin{pmatrix} \text{cos}\theta & -\text{sin}\theta \\ \text{sin}\theta & \text{cos}\theta \end{pmatrix}\]

• 여기서 반시계 방향으로 90도 회전은 (+90도) \(\theta\)에 90을 대입한 것과 같습니다.

• \[\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\]

• 반면 시계 방향으로 90도 회전은 (-90도) \(\theta\)에 -90을 대입한 것과 같습니다.

• \[\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}\]

• 그러면 위 행렬을 벡터 \(p_{r} - p_{l}\)에 곱하면 회전한 벡터를 구할 수 있고 회전한 벡터를 이용하여 외적의 성질을 이용하면 헤딩각을 구할 수 있습니다.

Autonomous Driving 관련 글 목록