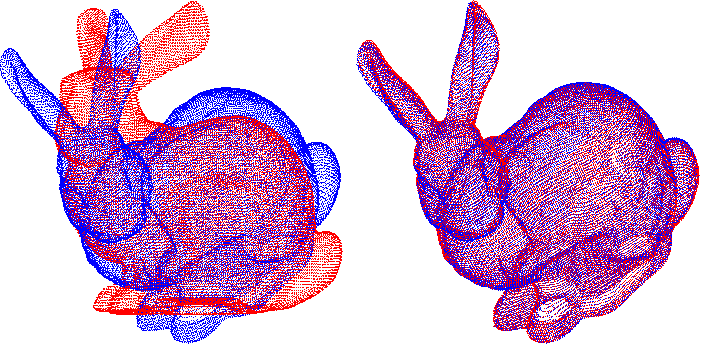
ICP (Iterative Closest Point) 와 Point Cloud Registration

이번 글에서는 이론적으로 ICP (Iterative Closest Point)에 대한 내용과 Cyrill Stachniss의 ICP 강의 내용을 정리해 보도록 하겠습니다..
강의는 총 1시간 분량의 강의 3개로 구성되어 총 3시간 분량의 강의입니다.
아래 참조 내용은 실제 코드 구현 시 도움 받은 내용입니다.

참조 : https://mr-waguwagu.tistory.com/36
참조 : https://github.com/minsu1206/3D/tree/main

Matched Points의 Point-to-Point ICP 개념

관련 논문 : Least-Squares Fitting of Two 3-D Point Sets

먼저 이번 글에서 다룰 강의 내용에 앞서서 간략하게 다룰 내용은 아래 강의 내용 중 Part 1: Known Data Association & SVD에 해당하는 내용입니다. 뒤의 강의 내용의 이해를 돕기 위하여 아래와 같이 먼저 정리하였습니다.

아래와 같이 2개의 점군 \(P, P'\) 가 있고 각 \(i\) 번째 점인 \(p_{i}, p'_{i}\) 가 서로 대응되는 것을 알고 있는 상황이라고 가정합니다.

\[P = {p_{1}, p_{2}, ... , p_{n}}\]
\[P' = {p'_{1}, p'_{2}, ..., p'_{n}}\]

위 점군에서 \(P\) 는 source에 해당하고 \(P'\) 는 destination에 해당합니다. 즉, \(P \to P'\) 로 변환하기 위한 관계를 알고자 하는 것이 핵심입니다.
따라서 \(P, P'\) 의 각 원소인 \(p_{i}, p'_{i}\) 의 관계를 알기 위해서는 Rotation을 위한 행렬 \(R\) 과 Translation을 위한 벡터 \(t\) 가 필요합니다.

\[\forall_{i} \ \ p'_{i} = Rp_{i} + t\]

이상적인 환경에서는 모든 \(i\) 에 대하여 \(p'_{i} = Rp_{i} + t\) 를 만족해야 하지만 현실적으로 오차가 포함되기 때문에 전체의 오차가 최소화 되는 방향으로 근사화 시키는 최적해를 구하는 방법을 이용하여 ICP를 적용합니다.
RGB-D 카메라를 이용하거나 이미지에서 Feature Extraction 및 Matching을 하여 점들끼리 쌍을 매칭한 점 군 \(P, P'\) 를 구한 경우에 지금부터 설명할 방법을 사용할 수 있습니다.

먼저 아래와 같이 \(i\) 점의 오차를 정의 합니다.

\[e_{i} = p'_{i} - (Rp_{i} + t)\]

풀어야 할 문제는 모든 에러 \(e_{i}\) 를 최소화 시키는 목적 함수를 만들고 목적 함수를 최소화 시키는 문제를 푸는 것입니다. 따라서 다음과 같이 오차 제곱 합의 목적 함수를 만듭니다.

\[\min_{R,t} \frac{1}{2} \sum_{i=1}^{n} \Vert (p'_{i} - (Rp_{i} + t)) \Vert^{2}\]

위 식에서 \(p_{i}, p'_{i}\) 는 벡터이기 때문에 norm을 적용하여 크기값인 스칼라 값으로 바꾸어서 목적 함수의 결과로 둡니다.
위 식을 좀 더 단순화하여 전개하기 위해 두 점군의 중심 위치 (centroid)를 정의해 보도록 하겠습니다.

\[p_{c} = \frac{1}{n} \sum_{i=1}^{n}(p_{i})\]
\[p'_{c} = \frac{1}{n} \sum_{i=1}^{n}(p'_{i})\]

앞에서 정의한 목적 함수에 ① \(-p'_{c} + Rp_{c} + p'_{c} -Rp_{c} = 0\) 을 추가한 뒤 ② 제곱식을 전개해 보도록 하겠습니다.

\[\begin{align} \frac{1}{2}\sum_{i=1}^{n} \Vert p'_{i} - (Rp_{i} + t) \Vert^{2} &= \frac{1}{2}\sum_{i=1}^{n} \Vert p'_{i} - Rp_{i} - t - p'_{c} + Rp_{c} + p'_{c} - Rp_{c} \Vert^{2} \\ &= \frac{1}{2}\sum_{i=1}^{n} \Vert (p'_{i} - p'_{c} - R(p_{i} - p_{c})) + (p'_{c} - Rp_{c} - t) \Vert^{2} \\ &= \frac{1}{2}\sum_{i=1}^{n} (\Vert p'_{i} - p'_{c} - R(p_{i} - p_{c}) \Vert^{2} + \Vert p'_{c} - Rp_{c} - t \Vert^{2} + 2(p'_{i} - p'_{c} - R(p_{i} - p_{c}))^{T}(p'_{c} - Rp_{c} - t)) \end{align}\]

위 식에서 다음 부분은 0이 됩니다.

\[\sum_{i=1}^{n} (p'_{i} - p'_{c} - R(p_{i} - p_{c})) = 0\]

왜냐하면 모든 \(p'_{i}\) 의 총합과 \(p'_{c}\) 를 \(n\) 번 더한 것과 값이 같고 모든 \(p_{i}\) 의 총합과 \(p_{c}\) 를 \(n\) 번 더한 것과 값이 같기 때문입니다.
따라서 앞에서 전개한 식에서 \(\sum_{i=1}^{n} (p'_{i} - p'_{c} - R(p_{i} - p_{c}))\) 부분을 소거하면 다음과 같이 정리 가능합니다.

\[\frac{1}{2}\sum_{i=1}^{n} (\Vert p'_{i} - p'_{c} - R(p_{i} - p_{c}) \Vert^{2} + \Vert p'_{c} - Rp_{c} - t \Vert^{2} + 2(p'_{i} - p'_{c} - R(p_{i} - p_{c}))^{T}(p'_{c} - Rp_{c} - t))\]
\[\frac{1}{2}\sum_{i=1}^{n} (\Vert p'_{i} - p'_{c} - R(p_{i} - p_{c}) \Vert^{2} + \Vert p'_{c} - Rp_{c} - t \Vert^{2})\]
\[\therefore \min_{R, t} J = \frac{1}{2}\sum_{i=1}^{n} ( \color{red}{\Vert p'_{i} - p'_{c} - R(p_{i} - p_{c}) \Vert^{2}} + \color{blue}{\Vert p'_{c} - Rp_{c} - t \Vert^{2}})\]

위 식의 빨간색 부분에 해당하는 항은 Rotation만 관련되어 있고 파란색 부분에 해당하는 항은 Rotation과 Translation 모두 관련되어 있지만 추가적으로 \(p_{c}, p'_{c}\) 만 연관되어 있습니다.
따라서 파란색 항은 Rotation만 구할 수 있으면 나머지 \(p_{c}, p'_{c}\) 는 주어진 점들을 통해 계산할 수 있으므로 \(\Vert p'_{c} - Rp_{c} - t \Vert^{2} = 0\) 으로 식을 두면 \(t\) 를 구할 수 있습니다.

빨간색 항 또한 조금 더 간단하게 만들기 위하여 다음과 같이 치환합니다.

\[q_{i} = p_{i} - p_{c}\]
\[q'_{i} = p'_{i} - p'_{c}\]

위 치환식의 정의에 따라서 \(q_{i}, q'_{i}\) 각각은 각 점 \(p_{i}, p'_{i}\) 가 점들의 중앙인 \(p_{c}, p'_{c}\) 로 부터 얼만큼 떨어져 있는 지 나타냅니다.
치환식을 이용하여 다음과 같은 2가지 스텝으로 Rotation과 Translation을 구해보도록 하겠습니다.

① Rotation \(R^{*}\) (예측값)를 다음 최적화 식을 통하여 구해보도록 하겠습니다.

\[R^{*} = \text{argmin}_{R} \frac{1}{2} \sum_{i=1}^{n} \Vert q'_{i} - R q_{i} \Vert^{2}\]

② 앞에서 구한 \(R^{*}\) 을 이용하여 \(t^{*}\) 을 구합니다.

\[t^{*} = p'_{c} - R^{*}p_{c}\]

먼저 ① 에 해당하는 \(R^{*}\) 을 구하는 방법에 대하여 살펴보도록 하겠습니다.

\[\begin{align} \frac{1}{2} \sum_{i=1}^{n} \Vert q'_{i} - R q_{i} \Vert^{2} &= \frac{1}{2} \sum_{i=1}^{n}(q'_{i} - R q_{i} )^{T}(q'_{i} - R q_{i} ) \\ &= \frac{1}{2} \sum_{i=1}^{n}(q{'}_{i}^{t}q{'}_{i} + q_{i}^{t}R^{t}Rq_{i} - q{'}_{i}^{t}Rq_{i} - q_{i}^{t}R^{t}q'_{i}) \\ &=\frac{1}{2} \sum_{i=1}^{n}(q{'}_{i}^{t}q{'}_{i} + q_{i}^{t}q_{i} - q{'}_{i}^{t}Rq_{i} - (q_{i}^{t}R^{t}q'_{i})^{t}) \quad (\because q_{i}^{t}R^{t}q'_{i} \text{ : scalar} ) \\ &= \frac{1}{2} \sum_{i=1}^{n}(q{'}_{i}^{t}q{'}_{i} + q_{i}^{t}q_{i} -q{'}_{i}^{t}Rq_{i} -q{'}_{i}^{t}Rq_{i}) \\ &= \frac{1}{2} \sum_{i=1}^{n}(q{'}_{i}^{t}q{'}_{i} + q_{i}^{t}q_{i} -2q{'}_{i}^{t}Rq_{i}) \end{align}\]

위 식에서 첫번째 항과 두번째 항은 \(R\) 과 관련이 없습니다. 따라서 실제 최적화를 위한 함수는 다음과 같이 변경될 수 있습니다.

\[\frac{1}{2} \sum_{i=1}^{n}(q{'}_{i}^{t}q{'}_{i} + q_{i}^{t}q_{i} -2q{'}_{i}^{t}Rq_{i}) \Rightarrow \frac{1}{2}\sum_{i=1}^{n} -2q{'}_{i}^{t}Rq_{i} = -\sum_{i=1}^{n}q{'}_{i}^{t}Rq_{i}\]

따라서 \(\min_{R, t} J\) 인 목적 함수를 최소화 하기 위해서는 \(\sum_{i=1}^{n}q{'}_{i}^{t}Rq_{i}\) 를 최대화하여 목적함수를 최소화 할 수 있도록 설계해야 합니다. 즉, \(\text{Maximize : } \sum_{i=1}^{n}q{'}_{i}^{t}Rq_{i}\) 를 만드는 것이 실제 풀어야할 최적화 문제가 됩니다.

그러면 \(\sum_{i=1}^{n}q{'}_{i}^{t}Rq_{i}\) 를 최대화 하기 위한 조건을 살펴보도록 하겠습니다.
식을 살펴보면 \(q_{i}, q'_{i}\) 는 벡터이고 \(R\) 은 3 x 3 크기의 행렬이므로 최종적으로 하나의 스칼라 값을 가지게 됩니다.
summation 내부의 결과가 스칼라 값이므로 trace 연산( \(\text{Trace}()\) )의 성질을 이용할 수 있습니다.
trace는 행렬의 대각 성분을 모두 더하는 연산입니다. 만약 최종 결과가 스칼라 값 (1 x 1 행렬)이고 이 값에 trace 연산을 적용하면 그 값 그대로 이기 때문에 값에 영향을 주지 않습니다. 따라서 결과값에 영향을 주지 않으면서 trace 연산의 성질들을 이용할 수 있습니다.
trace 연산의 Cyclic Permutation 성질은 다음을 만족합니다. 아래 기호 \(A, B, C\) 각각은 행렬입니다.

\[\text{Trace}(ABC) = \text{Trace}(CAB) = \text{Trace}(BCA)\]

이 성질을 이용하여 앞에서 전개하였던 \(\sum_{i=1}^{n} q_{i}^{T} R q'_{i}\) 의 식을 변경해 보도록 하겠습니다.

\[\begin{align} \sum_{i=1}^{n}q{'}_{i}^{t}Rq_{i} &= \text{Trace}\left(\sum_{i=1}^{n} q{'}_{i}^{t}Rq_{i} \right) \\ &= \text{Trace}\left(\sum_{i=1}^{n} q_{i}q{'}_{i}^{t}R \right) \\ &= \text{Trace}\left(\sum_{i=1}^{n} Rq_{i}q{'}_{i}^{t}\right) \\ &= \text{Trace}\left(R\sum_{i=1}^{n} q_{i}q{'}_{i}^{t}\right) \\ &= \text{Trace}(RH) \text{, where } \left(H = \sum_{i=1}^{n} q_{i}q{'}_{i}^{t}\right) \end{align}\]

위 식에서 \(q_{i} : (3 \times 1) \text{column vector}\) 이고 \(q{'}_{i}^{t} : (1 \times 3) \text{row vector}\) 이므로 \(\sum_{i=1}^{n} q_{i}q{'}_{i}^{t}\) 는 \(3 \times 3\) 행렬입니다. 따라서 SVD (Singular Value Decomposition)을 이용하여 행렬 분해를 할 수 있습니다. 특이값 분해 관련 내용은 아래 링크에 자세하게 설명되어 있습니다.
- 특이값 분해 : https://gaussian37.github.io/math-la-svd/

따라서 특이값 분해를 하면 다음과 같이 분해할 수 있습니다.

\[H = \sum_{i=1}^{n} q'_{i} q_{i}^{T} = U \Sigma V^{T}\]

여기서 \(U, V\) 는 orthonormal matrix이고 \(\Sigma\) 는 diagonal matrix이며 대각 성분은 특이값을 가집니다. 특이값과 고유값은 다음의 관계를 가집니다.

\[\text{singular value} = \sqrt{\text{eigen value}} > 0\]

SVD를 이용하여 분해한 값과 앞의 식을 이용하여 식을 좀 더 전개해 보도록 하겠습니다.

\[\text{Trace}(RH) = \text{Trace}(R \sum_{i=1}^{n} q'_{i} q_{i}^{T}) = \text{Trace}(R U \Sigma V^{t})\]

위 식에서 최종적으로 구해야 하는 값은 \(R\) 이며 \(\text{Trace}(RH)\) 가 최대화 되도록 \(R\) 을 잘 설정하면 문제를 해결할 수 있습니다.
결론적으로 \(R = VU^{T}\)이 최적해의 솔루션이 됩니다. 최적해를 찾는 과정을 이해하기 위하여 다음 소정리(Lemma)를 이용하도록 하겠습니다.
소정리를 이해하기 위하여 Positive Difinite Matrix의 이해가 필요합니다. 관련 정의는 아래 링크에서 참조하시기 바랍니다.
- 양의 정부호 행렬 (Positive Definite Matrix)

먼저 Positive Definite Matrix를 만족하는 \(AA^{t}\) 행렬과 orthonormal matrix \(B\) 가 있다고 가정하겠습니다. 이 때, 다음 식을 만족하는 것이 소정리 입니다.

\[\text{Trace}(AA^{t}) \ge \text{Trace}(BAA^{t})\]

행렬 \(A\) 의 \(i\) 번째 열벡터를 \(a_{i}\) 로 가정하겠습니다. 이 때, Trace의 Cycle Permutation 성질과 Trace의 정의를 이용하면 다음과 같이 식을 전개할 수 있습니다.

\[\begin{align} \text{Trace}(BAA^{t}) &= \text{Trace}(A^{t}BA) \\ &= \sum_{i}a_{i}^{t}(Ba_{i}) \end{align}\]

(Cauchy)Schwarz inequality를 이용하면 다음과 같이 식을 전개할 수 있습니다. (Cauchy)Schwarz inequality 정의는 다음과 같습니다.

\[\vert \langle u, v \rangle \vert \le \sqrt{\langle u, u \rangle} \cdot \sqrt{\langle v, v \rangle}\]
\[u, v \text{ : vector}\]
\[\langle u, v \rangle \text{ : inner product}\]

(Cauchy)Schwarz inequality 의 정의에 따라 아래 식을 전개해 보도록 하겠습니다.

\[a_{i}^{t}(Ba_{i}) \le \sqrt{(a_{i}^{t}a_{i})(a_{i}^{t}B^{t}Ba_{i})} = a_{i}^{t}a_{i} \quad (\because B \text{ : orthonormal matrix})\]
\[\therefore \ \text{Trace}(BAA^{t}) \le \sum_{i} a_{i}^{t}a_{i} = \text{Trace}({AA^{t}})\]

위 성질을 이용하여 앞에서 증명하던 내용을 이어서 증명해 보도록 하겠습니다.

\[H = U \Sigma V^{t}\]
\[U, V \text{ : orthonormal matrix}\]
\[\Sigma \text{ : diagonal matrix with singular value}\]
\[\text{Let } X = VU^{t}\]

위 식에서 \(X\) 는 orthonormal matrix 입니다. 왜냐하면 \(U, V\) 가 모두 orthonormal matrix이기 때문에 그 곱또한 orthonormal matrix를 만족하기 때문입니다.

\[X = VU^{t}\]
\[XH = VU^{t}U \Sigma V^{t} = V \Sigma V^{t}\]

Singular Value는 모두 0보다 크기 때문에 eigenvalue는 Singular Value의 제곱이므로 모든 eigenvalue는 양수임을 알 수 있습니다. eigenvlaue가 모두 양수이면 Positive Definite Matrix 조건을 만족하기 때문에 (양의 정부호 행렬 (Positive Definite Matrix) 참조) \(XH\) 는 Positive Definite Matrix 입니다.
따라서 앞에서 정리한 소정리를 이용할 수 있습니다.

\[\text{Trace}(XH) \ge \text{Trace}(BXH) \quad (\forall \text{ orthonormal matrix } B )\]

이 내용을 앞에서 정리한 식과 연결해서 설명해 보도록 하겠습니다.

\[\text{Trace}(RH) = \text{Trace}(VU^{T}H) \ge \text{Trace}(BRH)\]

즉, \(\text{Trace}(RH)\) 에서 \(R = VU^{T}\) 일 때, 모든 경우의 수에서 상한값을 가질 수 있으므로 최대화를 만족하기 위한 \(R^{*}\) 은 \(R^{*} = VU^{T}\) 을 통해서 구할 수 있습니다.
이 때, 구한 \(R\) 의 \(\text{det}()\) (determinant) 값은 +1이어야 합니다. 왜냐하면 \(R\) 은 orthonormal matrix이기 때문에 determinant가 +1을 만족하기 때문입니다. 하지만 -1이 도출되는 경우가 발생할 수 있습니다. 이 경우는 reflection이 발생한 경우이고 예외 케이스 입니다. 이 케이스를 처리하는 방법은 바로 뒤에서 살펴보도록 하겠습니다.

다음으로 ② 과정의 \(t^{*} = p'_{c} - R^{*}p_{c}\) 를 통해 간단하게 \(t^{*}\) 또한 구할 수 있습니다.

지금까지 살펴본 과정을 통해서 일반적인 상황에서의 Matched Points 쌍에 대한 Rotation과 Translation을 구할 수 있었습니다. 그리고 도출 과정을 보면 Rotation이 정상적으로 계산되면 Translation은 부가적으로 얻을 수 있기 때문에 Rotation을 잘 구하는 것이 핵심이 되는 것을 확인하였습니다.
그러면 Rotation을 정상적으로 구할 수 있는 경우와 그렇지 않은 경우를 구분하여 어떤 케이스가 존재하는 지 살펴보도록 하겠습니다.

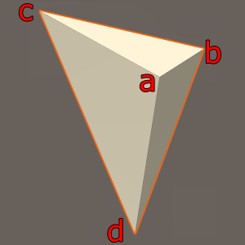
① \(q_{i}\) 가 coplanar가 아닌 경우 : 먼저 위 그림과 같이 점들이 하나의 평면에 있지 않는 경우가 가장 일반적인 상황입니다. 하나의 평면에 점들이 존재하는 상황을 coplanar라고 하며 위 그림과 같은 상황은 coplanar한 상황이 아닌 것으로 이해할 수 있습니다. 이 상황에서는 Rotation의 솔루션이 유일하게 존재하므로 SVD를 이용하여 구한 해를 정상적으로 사용할 수 있습니다.

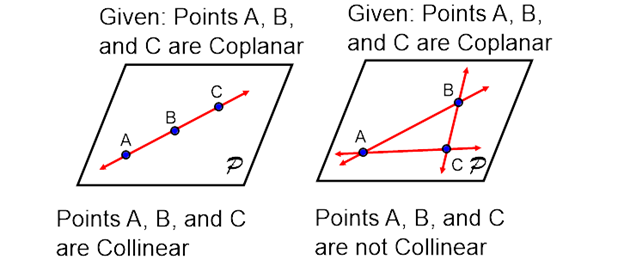
② \(q_{i}\) 가 colinear인 경우 : 두번째 케이스는 위 그림의 왼쪽과 같이 점들이 coplanar이면서 colinear인 경우 입니다. 이 경우에는 무한히 많은 rotation의 경우의 수를 만들어 낼 수 있습니다. 따라서 이와 같은 경우에는 유일한 해를 구할 수 없습니다. 따라서 사전에 모든 점들이 colinear인 지 확인해 보는 것이 중요합니다. 하지만 현실 데이터에서는 발생할 가능성이 매우 희박합니다.

③ \(q_{i}\) 가 coplanar이지만 colinear가 아닌 경우 : 마지막 케이스는 위 그림에서 오른쪽에 해당합니다. 점들이 coplanar이지만 colinear가 아닌 경우입니다. 이 경우에도 ①과 마찬가지 방법으로 해를 구할 수 있습니다.

최종적으로 구한 Rotation이 정말 Rotation으로써 의미를 가지려면 orthonormal matrix이고 determinant 또한 +1을 가져야 합니다.
하지만 경우에 따라서 determinant가 -1인 경우의 해를 얻을 수도 있습니다. 이와 같은 경우는 Rotation이 아니라 Reflection이 구해진 경우입니다.
determinant가 -1인 경우 2가지로 해석할 수 있습니다.
- ① coplanar인 상태에서 Reflection이 발생한 경우 \(V = [v_{1}, v_{2}, v_{3}] \to V = [v_{1}, v_{2}, -v_{3}]\) 로 변경하여 Rotation을 구할 수 있습니다. 이 때, \(\lambda_{3} = 0\) 을 만족해야 합니다.
- ② determinant가 -1임에도 불구하고 \(\lambda_{3} \ne 0\) 인 경우에는 해를 구할 수 없습니다. 이 경우에는 coplanar도 아니면서 Rotation을 구하는 최적화를 하는 데 실패한 경우에 해당합니다. 이와 같은 상황은 Noise가 많아서 Rotation을 구하기 어려우므로 Noise를 다루는 RANSAC과 같은 방법을 사용하는 작업이 필요합니다.

그러면 바로 위의 ①에 해당하는 상황을 살펴보도록 하겠습니다. coplanar에서는 모든 점들이 같은 평면에 있기 때문에, 차원이 하나 줄어든 것처럼 생각할 수 있습니다. 이 때, Rotation이 아닌 Reflection이 발생하더라도 만족할 수 있습니다.
모든 점들이 coplanar이면 앞에서 구한 \(H\) 의 Singular Value 하나가 0이 됩니다. 차원이 하나 소멸하기 때문에 발생한 문제이고 이와 같은 현상을 degeneracy라고 합니다.

\[H = \lambda_{1}u_{1}v'_{1} + \lambda_{2}u_{2}v'_{2} + 0 \cdot u_{3}v'_{3}\]
\[u_{i}, v_{i} \text{ : column vector of } U, V\]
\[\lambda_{1} > \lambda_{2} > \lambda_{3} = 0\]

따라서 위 케이스와 같이 행렬 분해가 된 경우 \(u_{3}\) 또는 \(v_{3}\) 의 부호를 바꾸더라도 \(H\) 에 영향을 주지 않습니다. 따라서 다음과 같이 \(V\) 를 변경합니다.

\[V = [v_{1}, v_{2}, v_{3}] \to V' = [v_{1}, v_{2}, -v_{3}]\]

최종적으로 \(R = V'U^{T}\) 를 이용하여 \(R\) 을 구함으로써 Rotation 을 정상적으로 구할 수 있습니다.

위 과정을 정리하면 다음과 같습니다.
① 행렬 \(H\) 를 구합니다.
② 행렬 \(H\) 의 SVD 적용을 한 후 \(H = U \Sigma V^{T}\) 로 분해합니다.
③ \(R = VU^{T}\) 를 이용하여 구합니다.
④ 만약 \(\text{det}(R) = 1\) 이면 정상적으로 Rotation이 구해진 상황입니다.
⑤ 만약 \(\text{det}(R) = -1\) 이면 다음 2가지로 해석할 수 있습니다.
- ⑤-1 \(\lambda_{3} = 0\) 이면 coplanar이므로 \(R = V'U^{T}\) 로 구할 수 있습니다.
- ⑤-2 \(\lambda_{3} \ne 0\) 이면 노이즈가 많아서 해를 구할 수 없는 상황입니다.

Matched Points의 Point-to-Point ICP Python Code

지금부터 살펴볼 내용은 임의의 Rotation과 Translation 그리고 점군 \(P\) 를 생성한 다음 생성한 Rotation과 Translation을 이용하여 \(P' = R*P + t\) 를 통해 \(P'\) 를 만들어 보겠습니다.
그 다음 \(P, P'\) 를 이용하여 ICP를 하였을 때, 생성한 Rotation과 Translation을 그대로 구할 수 있는 지 확인해 보도록 하겠습니다.

import numpy as np
from scipy.stats import special_ortho_group

def icp_svd(p_src, p_dst):
    """
    Calculate the optimal rotation (R) and translation (t) that aligns
    two sets of matched 3D points P and P_prime using Singular Value Decomposition (SVD).

    Parameters:
    - p_src: np.array of shape (3, n) -- the first set of points.
    - p_dst: np.array of shape (3, n) -- the second set of points.

    Returns:
    - R: Rotation matrix
    - t: Translation vector
    """
    # Step 1: Calculate the centroids of P and P_prime
    centroid_p_src = np.mean(p_src, axis=1, keepdims=True)  # Centroid of P    
    centroid_p_dst = np.mean(p_dst, axis=1, keepdims=True)  # Centroid of P'   

    # Step 2: Subtract centroids
    q_src = p_src - centroid_p_src    
    q_dst = p_dst - centroid_p_dst

    # Step 3: Construct the cross-covariance matrix H
    H = q_src @ q_dst.T

    # Step 4: Perform Singular Value Decomposition
    U, Sigma, Vt = np.linalg.svd(H)
    V = Vt.T

    # Step 5: Calculate rotation matrix R    
    R_est = V @ U.T

    result = True
    # Step 6: Ensure R is a proper rotation matrix
    det_R_est = np.linalg.det(R_est)
    if np.abs(det_R_est - (-1)) < 0.0001: # check detminant
        if np.abs(Sigma[-1]) < 0.00001 == 0: # check reflection
            # Reflection in coplanar cse
            V[:,-1] *= -1  # Flip the sign of the last column of V
            R_est = V @ U.T
        else:
            # can't get rotation matrix
            result = False

    # Step 7: Calculate translation vector t        
    t_est = centroid_p_src - R_est @ centroid_p_dst
    t_est = t.reshape(3, 1)

    return R_est, t_est, result

# Example usage with dummy data
# Define the set of points P
P = np.random.rand(3, 30) * 100

# Set a random Rotation matrix R (ensuring it's a valid rotation matrix)
R = special_ortho_group.rvs(3)

# Set a random Translation vector t
t = np.random.rand(3, 1) * 10

# Apply the rotation and translation to P to create P_prime
P_prime = R @ P + t

################################### Calculate R and t using ICP with SVD
R_est, t_est, _ = icp_svd(P, P_prime)

print("R : \n", R)
print("R_est : \n", R_est)
print("R and R_est are same : ", np.allclose(R,R_est))
print("\n")

# R : 
#  [[-0.65800821  0.75067865 -0.05921784]
#  [-0.56577368 -0.54475838 -0.61898179]
#  [-0.49691583 -0.3737912   0.78316971]]
# R_est : 
#  [[-0.65800821  0.75067865 -0.05921784]
#  [-0.56577368 -0.54475838 -0.61898179]
#  [-0.49691583 -0.3737912   0.78316971]]
# R and R_est are same :  True

print("t : \n", t)
print("t_est : \n", t_est)
print("t and t_est are same : ", np.allclose(t, t_est))
print("\n")

# t : 
#  [[7.19317157]
#  [5.15828552]
#  [2.92487954]]
# t_est : 
#  [[7.19317157]
#  [5.15828552]
#  [2.92487954]]
# t and t_est are same :  True

위 코드의 결과와 같이 정상적으로 \(R, t\) 를 구할 수 있음을 확인하였습니다.

지금까지 살펴본 방법은 매칭이 주어질 때, \(R, t\) 를 추정하는 문제에 해당합니다.
매칭을 알고있는 경우에는 최소 제곱 문제를 해결하기 위한 analytic solution이 존재하기 때문에 numerical solution을 이용한 최적화가 반드시 필요하진 않습니다.
하지만 점들의 매칭에 오류가 있거나 점들의 \(X, Y, Z\) 값이 부정확한 outlier가 포함되면 ICP를 진행하는 데 방해가 될 수 있습니다. 따라서 별도의 outlier를 제거해야 좋은 \(R, t\) 값을 구할 수 있으므로 outlier 제거 알고리즘인 RANSAC을 적용하여 정상적인 \(R, t\) 를 구하는 방법에 대하여 알아보도록 하겠습니다.
RANSAC과 관련된 내용은 아래 링크를 참조하시기 바랍니다.
- RANSAC : https://gaussian37.github.io/vision-concept-ransac/

RANSAC을 이용할 때에는 추출할 샘플 갯수, 반복 시험 횟수, inlier threshold를 파라미터로 필요로 합니다. 그 부분은 추가적인 실험이나 위에서 공유한 RANSAC 개념 링크의 글을 통해 어떻게 파라미터를 셋팅하는 지 참조할 수 있습니다.
아래 코드는 앞선 예제 코드에서 outlier 데이터를 추가한 뒤 RANSAC 과정을 거쳐서 좀 더 강건하게 Rotation과 Translation을 구하는 예제입니다.

import numpy as np
from scipy.stats import special_ortho_group

def icp_svd(p_src, p_dst):
    """
    Calculate the optimal rotation (R) and translation (t) that aligns
    two sets of matched 3D points P and P_prime using Singular Value Decomposition (SVD).

    Parameters:
    - p_src: np.array of shape (3, n) -- the first set of points.
    - p_dst: np.array of shape (3, n) -- the second set of points.

    Returns:
    - R: Rotation matrix
    - t: Translation vector
    """
    # Step 1: Calculate the centroids of P and P_prime
    centroid_p_src = np.mean(p_src, axis=1, keepdims=True)  # Centroid of P    
    centroid_p_dst = np.mean(p_dst, axis=1, keepdims=True)  # Centroid of P'   

    # Step 2: Subtract centroids
    q_src = p_src - centroid_p_src    
    q_dst = p_dst - centroid_p_dst

    # Step 3: Construct the cross-covariance matrix H
    H = q_src @ q_dst.T

    # Step 4: Perform Singular Value Decomposition
    U, Sigma, Vt = np.linalg.svd(H)
    V = Vt.T

    # Step 5: Calculate rotation matrix R    
    R_est = V @ U.T

    result = True
    # Step 6: Ensure R is a proper rotation matrix
    det_R_est = np.linalg.det(R_est)
    if np.abs(det_R_est - (-1)) < 0.0001: # check detminant
        if np.abs(Sigma[-1]) < 0.00001 == 0: # check reflection
            # Reflection in coplanar cse
            V[:,-1] *= -1  # Flip the sign of the last column of V
            R_est = V @ U.T
        else:
            # can't get rotation matrix
            result = False

    # Step 7: Calculate translation vector t        
    t_est = centroid_p_src - R_est @ centroid_p_dst
    t_est = t.reshape(3, 1)

    return R_est, t_est, result

def icp_svd_ransac(points_source, points_destination, n=3, num_iterations=20, inlier_threshold=0.01):
    # n = 3  # Number of points to estimate the model, for affine 3D at least 4 points
    # num_iterations = 20  # Number of iterations
    # inlier_threshold = 0.1  # Inlier threshold, this might be a count or a percentage based on your needs
    best_inliers = -1
    best_R = None
    best_t = None

    for _ in range(num_iterations):
        # Step 1: Randomly select a subset of matching points
        indices = np.random.choice(points_source.shape[1], n, replace=False)
        points_src_sample = points_source[:, indices]        
        points_dst_sample = points_destination[:, indices]

        # Step 2: Estimate rotation and translation using SVD based ICP
        R, t, result = icp_svd(points_src_sample, points_dst_sample)
        
        # Step 3 and 4: Calculate error and inliers
        points_src_transformed = R @ points_source + t
        errors = np.linalg.norm(points_destination - points_src_transformed, axis=0)
        inliers = np.sum(errors < inlier_threshold)

        # Step 5: Check if current iteration has the best model
        if inliers > best_inliers:            
            best_inliers = inliers
            best_R = R
            best_t = t

        # Step 6: Check terminating condition
        if best_inliers > inlier_threshold or _ == num_iterations - 1:
            break

    return best_R, best_t, best_inliers

# Example usage with dummy data
# Define the set of points P
P = np.random.rand(3, 30) * 100

# Set a random Rotation matrix R (ensuring it's a valid rotation matrix)
R = special_ortho_group.rvs(3)

# Set a random Translation vector t
t = np.random.rand(3, 1) * 10

# Apply the rotation and translation to P to create P_prime
P_prime = R @ P + t

# Add outliers to P_prime to create P_prime2
num_outliers = 10
P_prime2 = P_prime.copy()
P_prime2[:, -num_outliers:] = np.random.rand(3, num_outliers) * 100

################################## Calculate R and t using ICP with SVD, plus RANSAC
R_est, t_est, _ = icp_svd(P, P_prime2)

print("ICP without RANSAC : \n")
print("R : \n", R)
print("R_est : \n", R_est)
print("R and R_est are same : ", np.allclose(R,R_est))
print("\n")

# R : 
#  [[-0.65800821  0.75067865 -0.05921784]
#  [-0.56577368 -0.54475838 -0.61898179]
#  [-0.49691583 -0.3737912   0.78316971]]
# R_est : 
#  [[-0.33635851  0.94169333 -0.00875314]
#  [-0.70013826 -0.25627327 -0.66643111]
#  [-0.62981693 -0.21803137  0.74551523]]
# R and R_est are same :  False

print("t : \n", t)
print("t_est : \n", t_est)
print("t and t_est are same : ", np.allclose(t, t_est))
print("\n")

# t : 
#  [[7.19317157]
#  [5.15828552]
#  [2.92487954]]
# t_est : 
#  [[7.19317157]
#  [5.15828552]
#  [2.92487954]]
# t and t_est are same :  True

print("diff R and R_est : \n", np.linalg.norm(np.abs(R - R_est)))
print("\n")

# diff R and R_est : 
#  0.5379242095232378

R_est, t_est, inliers = icp_svd_ransac(P, P_prime2)
print("ICP with RANSAC : \n")
print("R : \n", R)
print("R_est : \n", R_est)
print("R and R_est are same : ", np.allclose(R,R_est))
print("\n")

# R : 
#  [[-0.65800821  0.75067865 -0.05921784]
#  [-0.56577368 -0.54475838 -0.61898179]
#  [-0.49691583 -0.3737912   0.78316971]]
# R_est : 
#  [[-0.65800821  0.75067865 -0.05921784]
#  [-0.56577368 -0.54475838 -0.61898179]
#  [-0.49691583 -0.3737912   0.78316971]]
# R and R_est are same :  True

print("t : \n", t)
print("t_est : \n", t_est)
print("t and t_est are same : ", np.allclose(t, t_est))
print("\n")

# t : 
#  [[7.19317157]
#  [5.15828552]
#  [2.92487954]]
# t_est : 
#  [[7.19317157]
#  [5.15828552]
#  [2.92487954]]
# t and t_est are same :  True

print("diff R and R_est : \n", np.linalg.norm(np.abs(R - R_est)))
print("\n")

# diff R and R_est : 
#  1.7603605962323948e-15

print("num inliers : ", inliers)
# num inliers :  20

icp_svd_ransac을 통하여 outlier의 비율이 꽤 큰 경우에도 정상적인 Rotation, Translation을 추정할 수 있음을 확인하였습니다.
지금까지 살펴본 내용은 두 점군의 쌍을 매칭할 수 있을 때, analytic solution을 이용하여 최적해를 구하는 방법에 대하여 알아보았습니다.

Part 1: Known Data Association & SVD

위 내용은 앞에서 다룬 Matched Points의 Point-to-Point ICP 개념과 일치합니다.

ICP (Iterative Closest Point) 와 Point Cloud Registration

목차

Matched Points의 Point-to-Point ICP 개념

Matched Points의 Point-to-Point ICP Python Code

Part 1: Known Data Association & SVD

Part 2: Unknown Data Association

Part 3: Non-linear Least Squares

Matched Points의 Point-to-Point ICP 개념

Matched Points의 Point-to-Point ICP Python Code

Part 1: Known Data Association & SVD

Part 2: Unknown Data Association

Part 3: Non-linear Least Squares