베이즈 필터 (Bayes Filter)
2020, Feb 01
- 선수 지식 1 : 상태 방정식 (state equation)
- 선수 지식 2 : 자율주행에서의 Localization과 Tracking
- 선수 지식 3 : 베이지안 통계
- 참조 1 : Probabilistic Robotics (Sebastian Thrun)
-
참조 2 : 순천향 대학교 박성근 교수님 강의
- 이번 글에서는 Bayes Filter에 대하여 다루어 보도록 하겠습니다. Bayes Filter는 Kalman Filter와 Particle Filter 개념의 기초가 되는 간단하지만 매우 중요한 Filter입니다. 따라서 Kalman Filter나 Particle Filter를 배우기 전 단계라면 베이즈 필터를 통하여 최적 상태를 추정하는 필터들이 어떻게 동작하는 지 그 메커니즘을 먼저 배우기를 추천합니다.
- 만약 Kalman Filter와 Particle Filter에 대하여 잘 아신다면 아래 Bayes Filter의 개념과 비교해 보는 것을 추천 드립니다.
목차
-
Bayes Filter 개념
-
로봇 이동 예제를 통한 Bayes Filter 이해
-
Bayes Filter 알고리즘의 이해
-
Bayes Filter 수식의 이해
-
로봇 이동 예제를 통한 Bayes Filter 수식의 이해
-
자동차 이동 예제를 이용한 Bayes Filter 수식의 이해
-
Bayes Filter의 한계와 개선 방법
Bayes Filter 개념
- 먼저 이 글에서 다룰
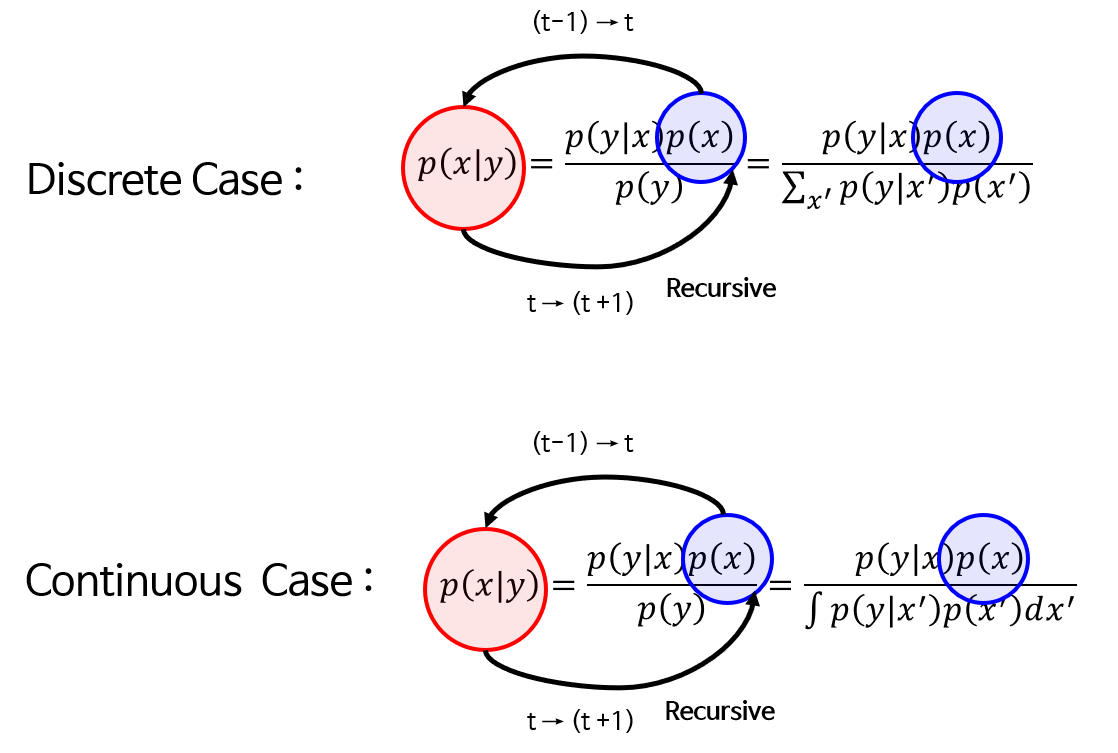
Bayes Filter는Bayes Theorem을Recursive하게 따릅니다. - 즉, 확률 기반의 Recursive한 Filter라고 보시면 됩니다. Bayes Theorem을 이용하면
prior와likelihood를 이용하여posterior를 구할 수 있습니다. Recursive 하다는 것은 지금 구한posterior가 다음 스텝에서prior로 사용된다는 것을 뜻합니다. - Bayes Filter의 식은 다음과 같습니다.
- 이러한 Bayes Filter의 목적을 단 한줄의 수식으로 표현하면 다음과 같습니다.
- \[bel(x_{t}) = p(x_{t} \vert z_{1:t}, u_{1:t})\]
- 위 식을 해석하면 \(x_{t}\)는 t시점의
상태 값을 \(z_{t}\)는센서 입력 값을 뜻하고 \(u_{t}\)는제어 입력값을 뜻합니다. - 따라서 알고리즘의 시작부터 현재 시점 \(t\) 까지의 센서 입력값과 제어 입력값을 이용하여 현재 상태를 확률적으로 추정하는 것으로 해석할 수 있습니다.
- 즉,
Bayes Filter는 기본적으로 센서값, 제어값을 이용하여 현재 상태를 추정하는 알고리즘이고 이 개념은 그대로Kalman Filter와Particle Filter에도 적용될 수 있습니다.
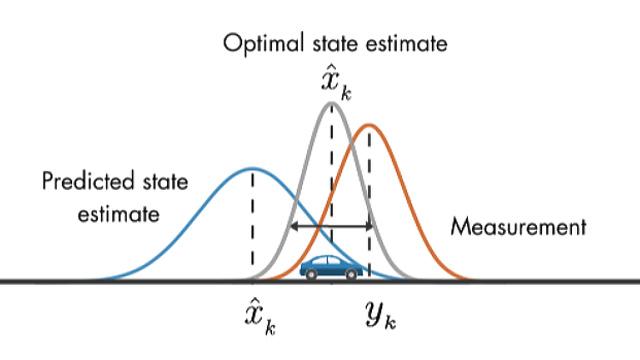
- Bayes Filter를 조금 더 자세하게 들여다 보면 Bayes Filter는 2가지 역할을 합니다.
- 첫번째는 이전 상태와 제어값을 이용하여 현재 상태를 예측하는 역할이고 두번째는 Bayes Rule을 이용하여 센서 입력값을 현재 상태에 반영하는 역할입니다.
- 첫번째 케이스를
물리 모델을 통한 예측이라고 하겠습니다. 왜냐하면 이전 상태값에 물리 모델의 수식(ex. 속력 = 이동한 거리 / 시간)을 통해 현재 상태를 예측하기 때문입니다. 이 때,제어값이 사용됩니다. - 그리고 두번째 케이스는
센서값을 통한 예측이라고 하겠습니다. - 자동차가 이동하는 사례를 이용하여 예를 들어보겠습니다. 이 때, 상태의 정의는 자동차의 위치라고 가정하겠습니다.
물리 모델을 통한 예측: 고속도로에서 이동 중인 자차의 1초 전의 상태에서 현재 상태를 예측할 때, 자동차의 1초 전의 위치와 자동차의 속도 정보 및 추가적으로 입력된 엑셀 및 브레이크제어값을 이용하여 자동차의 현재 위치를 예측할 수 있습니다.센서값을 통한 예측: GPS를 이용하여 자동차의 현재 위치를 알 수 있습니다.
- Bayes Filter는 위 값 중 하나만을 사용하는 것이 아니라 두가지 값을 모두 사용하여 하나의 값으로 퓨전하여 사용합니다. 예를 들면 ① 현재 위치를 이전 위치 상태 + 속도 물리 모델 + 제어값을 이용하여 먼저 예측하고 ② 그 위치에 센서값을 통해 보완합니다.
- 이 퓨전 방법을 통하여
물리 모델을 통한 예측만 사용하거나센서값을 통한 예측만 사용하는 것 보다 더 좋은 성능으로 현재 상태를 추정할 수 있습니다. - 위 두가지 값을 퓨전할 때, 노이즈가 작은 값을 더 신뢰하여 반영하는 것이 높은 성능을 확보하기 위해 고려할 점입니다. 경우에 따라서 물리 모델이 정확할 수 있고 센서의 성능이 좋을 수도 있기 때문에 이것은 상황에 맞춰서 적용해야합니다.
- 이 내용은 선수 지식 1의 상태 방정식 내용을 자세히 읽어보시길 권장드립니다.
로봇 이동 예제를 통한 Bayes Filter 이해
- 앞에서 설명한 컨셉을 Probabilistic Robotics의 로봇 예제를 이용하여 알아보도록 하겠습니다.
Step 1

- 위 그림은 로봇이 어느 위치에 있는 지 확률 분포 값으로 표현합니다. 위 그래프에서 \(x\) 가로축과 \(bel(x)\) 세로축으로 이루어진 확률 분포를 살펴보면 모든 위치가 동일한 확률 값을 아주 낮게 가집니다. 즉, 초기값은 어떠한 정보가 없으므로 uniform 분포를 가지게 됩니다.
- 각 문 앞에는 센서가 있습니다. 문 앞의 센서는 로봇이 지나갈 때, 3개의 문 중 하나에 로봇이 있다고 판단을 할 수 있으나 어느 문 앞에 로봇이 존재하는지는 판단할 수는 없습니다. 즉, 로봇이 문 앞에 있을 때, 3개의 문 모두 동일한 확률 분포가 추가됩니다.
- 로봇은 왼쪽에서 오른쪽으로 이동 중에 있습니다.
Step 2
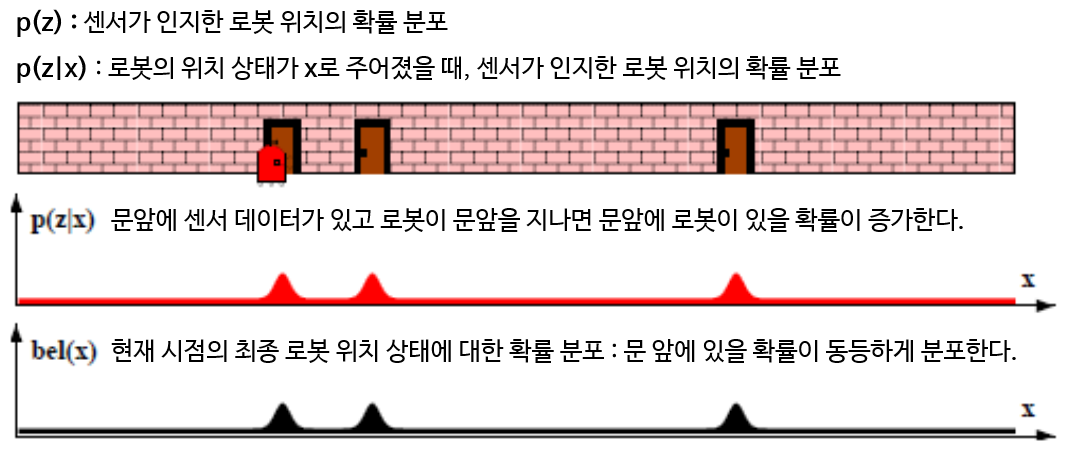
- 위 그림과 같이 새로운 확률 분포에 대한 개념을 정의해 보도록 하겠습니다.
- \(p(z)\) : 센서가 인지한 로봇 위치의 확률 분포
- \(p(z \vert x)\) : 로봇의 위치 상태가 \(x\)로 주어졌을 때, 센서가 인지한 로봇 위치의 확률 분포
- 위 그림에서 \(p(z \vert x)\)는 문앞에 센서가 있고 로봇이 문앞을 지나면 문앞에 로봇이 있을 확률이 증가하게 됩니다.
- 따라서 현재 시점의 최종 로봇 위치 상태에 대한 확률 분포는 문 앞에 있을 확률이 동등하게 분포하게 됩니다.
- 센서가 인지하였음에도 불구하고 문 앞의 확률 분포가 매우 좁게 (분산이 작게) 분포하지 못하는 이유는 센서에 존재하는 노이즈 때문입니다.
Step 3
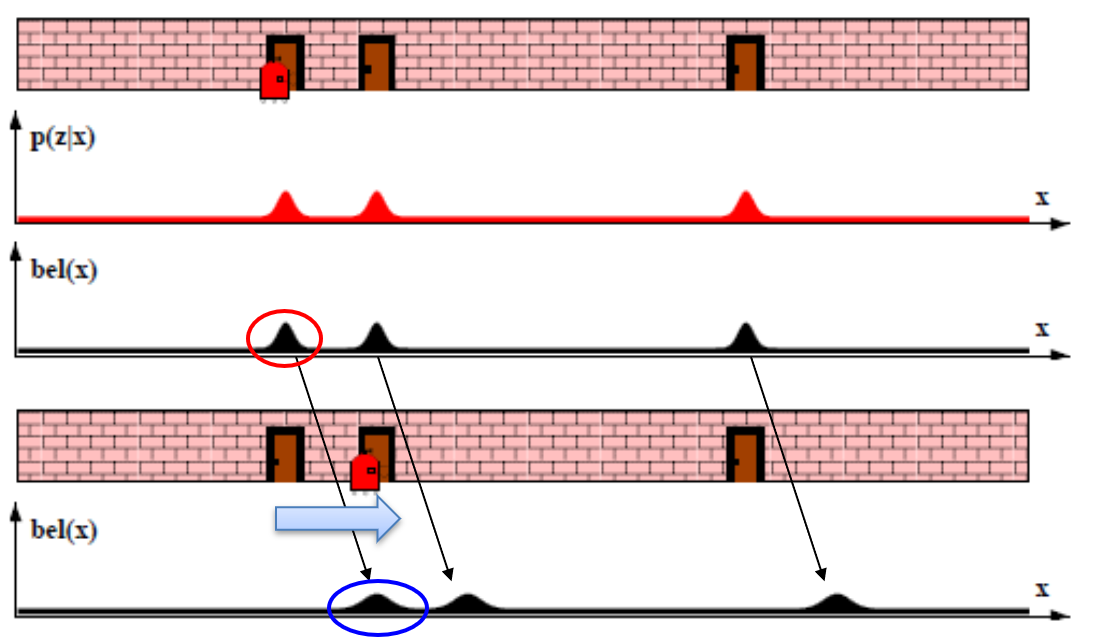
- Step 2의 상태에서 Step 3로 로봇이 오른쪽으로 이동함에 따라 Step2에서 얻은 위치의 확률 분포가 로봇이 오른쪽으로 이동한 만큼 그대로 이동한 것을 확인할 수 있습니다.
- 이 결과는 앞에서 설명한
물리 모델을 통한 예측을 한 것으로 파악할 수 있습니다. 위치 속도 모델과 엑셀 및 브레이크와 같은 제어값을 이용하여 물체의 위치 상태를 예측한 것입니다. - 그리고 단순히 오른쪽으로 분포가 이동한 것 뿐만 아니라 확률 분포의 분산이 조금 더 커진 것을 알 수 있습니다. 빨간색 동그라미의 확률 분포에 비해서 파란색 동그라미의 확률 분포가 조금 더 퍼져 있는 것을 확인하시면 됩니다.
- 이와 같이 분산이 더 커진 이유는 제어값에 존재하는 노이즈가 추가되었기 때문입니다. 그 결과 Step 2의 센서 노이즈에 Step 3 의 제어 노이즈 까지 추가됩니다.
Step 4
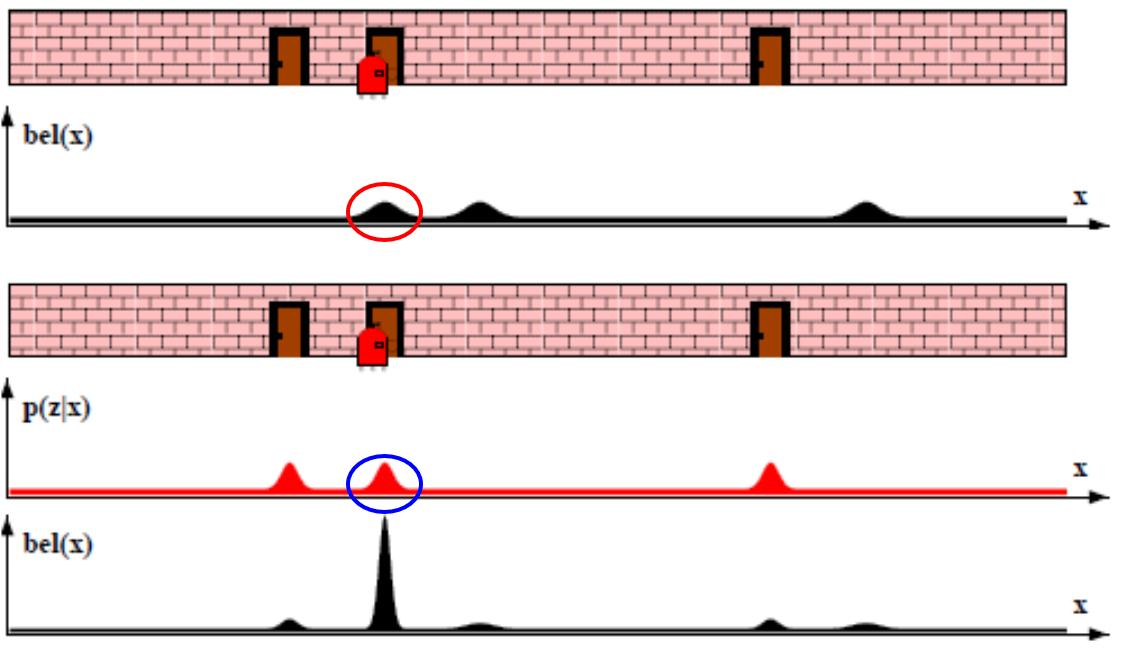
- 이번 Step에서는 Step 3까지 반영한 \(bel(x)\)에 센서가 인지한 로봇의 위치에 대한 확률 분포를 결합합니다.
- 위 그림과 같이 기존의 \(bel(x)\)와 센서값 \(p(z \vert x)\)가 결합하여 새로운 \(bel(x)\)를 계산합니다.
- 계산 결과 빨간색 동그라미의 확률과 파란색 동그라미의 확률이 겹치게 되어 새로운 \(bel(x)\)에서는 로봇의 위치 확률이 커지고 분산이 작아지게 됩니다.
Step 5
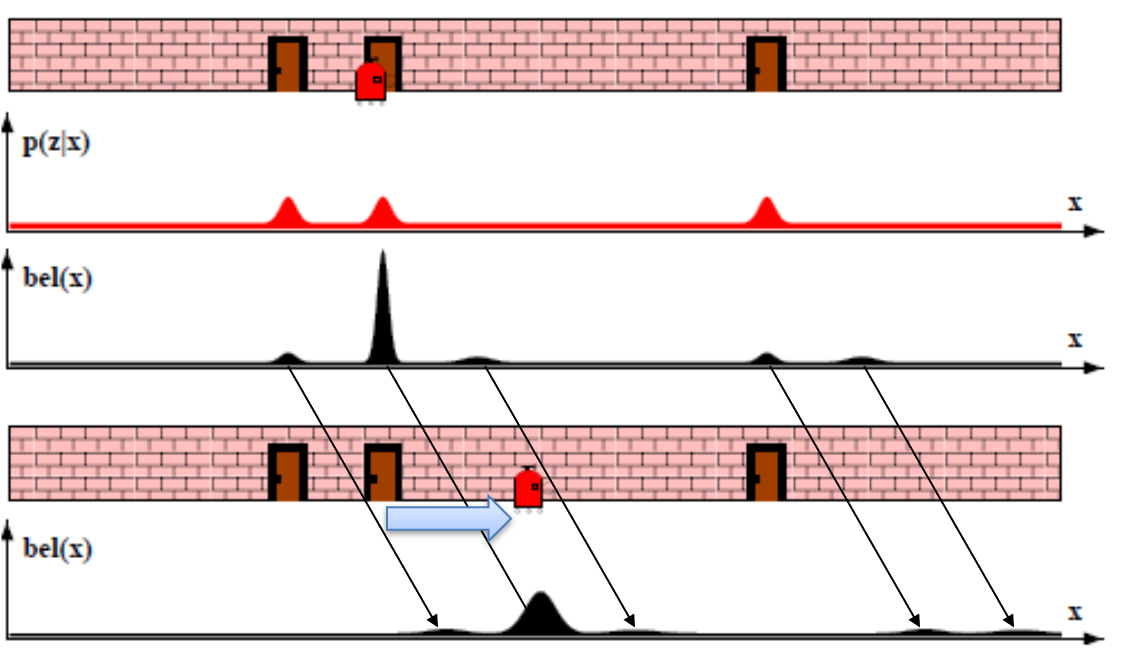
- 이번 Step에서도 Step 3과 같이
물리 모델을 통한 예측을 합니다. 따라서 로봇이 이동한 거리 만큼 확률 분포가 이동한 것을 확인할 수 있습니다. - 또한 Step 3에서와 같이 물리 모델에 사용된 제어값에 대한 노이즈가 기존 확률 분포에 추가되어 각 위치 별 분포의 분산이 커진 것을 확인 할 수 있습니다.
- 지금까지 확인한 내용이 Bayes Filter의 가장 기본적인 컨셉입니다.
- 상태가 변화할 때,
물리 모델을 통한 예측을 통하여 현재 상태를 예측하고, 이와 연관된 센서값이 있으면센서값을 통한 예측을 통하여 현재 상태를 보완해 줍니다. - 이 과정을 좀 더 수식 상에서 상세하게 알아보도록 하겠습니다.
Bayes Filter 알고리즘의 이해
- 로봇 이동 예제를 통하여 확인한 Bayes Filter 알고리즘을 정형화하여 살펴보도록 하겠습니다.

- 핵심이 되는 알고리즘은 for문 안의 2줄 밖에 되지 않을 정도로 매우 간단합니다.
- for 문의 첫번째 줄은
contorl update또는prediction이라고 불립니다. 앞의 예제에서물리 모델을 통한 예측부분에 해당하는 알고리즘 입니다.control update라고 불리는 이유는 제어값을 사용하여 상태를 업데이트 하였기 때문이고prediction이라고 하는 이유는 물리 모델과 제어값을 이용하여 현재 상태를예측하였기 때문입니다. - for 문의 두번째 줄은
measurement update또는correction이라고 불립니다. 이 부분은 앞의 예제에서센서값을 통한 예측을 이용하여 현재 상태 보정에 해당하는 알고리즘 입니다.measurement update라고 불리는 이유는 센서를 통해측정한 값을 사용하여 업데이트 하기 때문이고correction이라고 하는 이유는 prediction한 결과를 센서값을 통하여 보정하기 때문입니다.
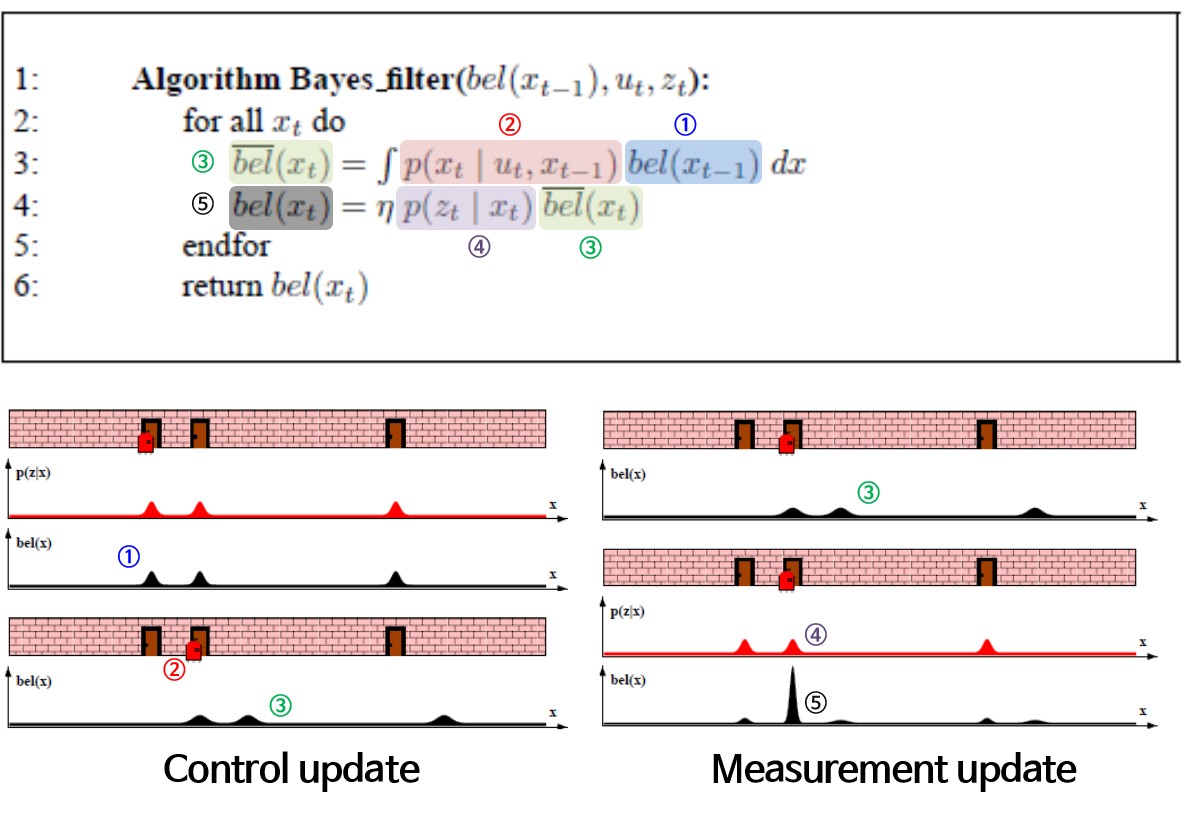

- 위 식을 통해 앞에서 설명한 모든 내용을 이해하실 수 있습니다.
- ①과 ②를 이용하여 ③ control update (prediction)을 계산하고 ③과 ④를 이용하여 ⑤ measurement update (correction)를 합니다.
- 최종적으로 얻은 ⑤ measurement update를 다음 step의 입력으로 사용하여 recursive하게 filter를 구성할 수 있습니다.
Bayes Filter 수식의 이해
- 앞에서 다룬 Bayes Filter의 수식을 좀 더 자세하게 분석해 보도록 하겠습니다.
- 먼저 Bayes Filter에서 사용 되는 데이터는 관측값 \(z\) 와 제어값 \(u\)가 사용됩니다. 따라서 각 time의 \(t\) 마다 \(z\)와 \(u\)가 연속적으로 입력되는 형태를 가집니다.
- \[d_{t} = {u_{1}, z_{1}, ... , u_{t}, z_{t}}\]
- 위 데이터를 이용하여 각각의 모델을 표현하면 다음과 같이 표현할 수 있었습니다.
- 센서 모델 : \(p(z_{t} \vert x_{t})\)
- 상태 모델 : \(p(x_{t} \vert x_{t-1}, u_{t})\)
- 시스템 상태의 사전 확률 분포 : \(p(x)\)
- 이 때, 구해야 하는 값은 상태의
Posterior로 \(Bel(x_{t}) = p(x_{t} \vert u_{1}, z_{1}, \cdots , u_{t}, z_{t})\)로 나타낼 수 있습니다.
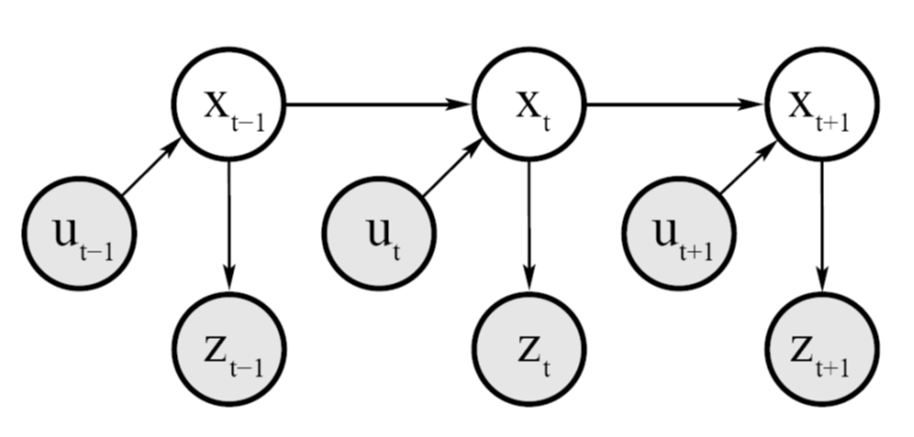
- 이상적으로는 사후 확률 \(Bel(x_{t}) = p(x_{t} \vert u_{1}, z_{1}, \cdots , u_{t}, z_{t})\) 식과 같이 알고리즘이 시작한 시점부터 현재 시점 까지의 \(u_{1:t}, z_{1:t}\)를 모두 사용하는 것이 맞습니다.
- 하지만 여기서
Markov Assumption을 도입하여 문제를 좀 더 간단히 만들 수 있습니다. 이 가정은 모든 \(u\)와 \(z\)가 독립임을 가정하고 업데이트된 \(bel(x_{t})\)들은 그 이전의 정보를 함축하고 있다고 가정하는 것입니다. - 따라서 Bayes Filter는 \(z_{1:t}, u_{1:t}\) 대신 현재 입력된 센서 및 제어값인 \(z_{t}, u_{t}\)과 바로 직전 상태의 상태값인 \(bel(x_{t-1})\)을 사용합니다.

- 다시 위 식에 대하여 살펴보겠습니다.
- 3행은 \(\overline{bel}(x_{t}) = p(x_{t} \vert z_{1:t-1}, u_{1:t})\)를 만족합니다. 왜냐하면 이는 현재 센서값 없이 추정한 현재 상태이기 때문입니다.
- 반면 4행은 \(bel(x_{t}) = p(x_{t} \vert z_{1:t}, u_{1:t})\) 를 만족합니다. 즉, 3행에서 센서값까지 고려한 것으로 나타납니다.
- 그러면 이 식들이 어떻게 위 식의 알고리즘과 같이 전개될 수 있는 지 살펴보겠습니다.
- 먼저 \(p(x_{t} \vert z_{1:t-1}, u_{1:t})\)을 전개하여 3행의 식 \(\overline{bel}(x_{t})\)을 유도해 보겠습니다.
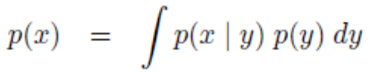
- 식을 전개 하기 위해서는 위 식과 같이 베이지안 확률의
total probability 법칙을 이용하겠습니다.
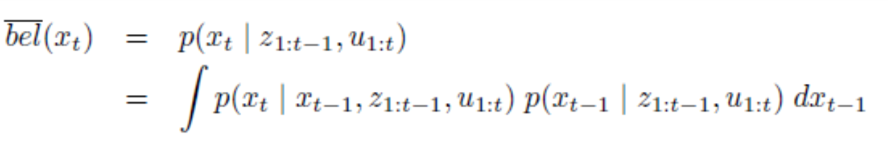
- 위 식과 같이 \(x_{t-1}\)을 이용하여 total probability를 적용하여 전개할 수 있습니다.
- 위 식에서 \(p(x_{t} \vert x_{t-1}, z_{1:t-1}, u_{1:t})\)와 \(p(x_{t-1} \vert z_{1:t-1}, u_{1:t})\) 각각은 다음과 같이 전개될 수 있습니다.
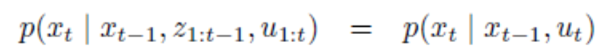
- 이와 같이 전개될 수 있는 이유는
Markov Assumption을 가정하기 때문에 \(x_{t-1}\)이 \(z_{1:t-1}, u_{1:t-1}\)을 포함하기 때문입니다. 따라서 조건부에는 \(x_{t-1}, u_{t}\)만 남게 됩니다.
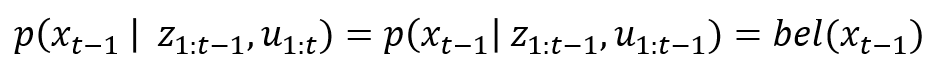
- 위 식에서는 대상이 \(x_{t-1}\)이기 때문에 미래에 발생할 \(u_{t}\)를 사용하여 확률을 나타낼 수 없습니다. 따라서 \(u_{t}\)는 생략할 수 있어서 \(p(x_{t-1} \vert z_{1:t-1}, u_{1:t-1})\)로 표현할 수 있습니다.
- 정리된 식은 최종적으로 bel 함수의 정의에 따라 \(bel(x_{t-1})\)로 나타낼 수 있습니다.

- 이와 같은 방식으로 Bayes Filter의 control update (prediction) 부분의 식 전개를 할 수 있습니다.
- 이번에는 \(p(x_{t} \vert z_{1:t}, u_{1:t})\)을 전개하여 4행의 식 \(bel(x_{t})\)를 유도해 보겠습니다.
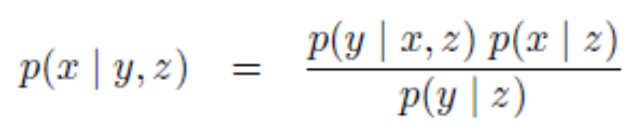
- 먼저 위 식의 성질을 이용하여 식을 전개하겠습니다. 아래 식의 첫번째 줄의 식에서 사용되었습니다.
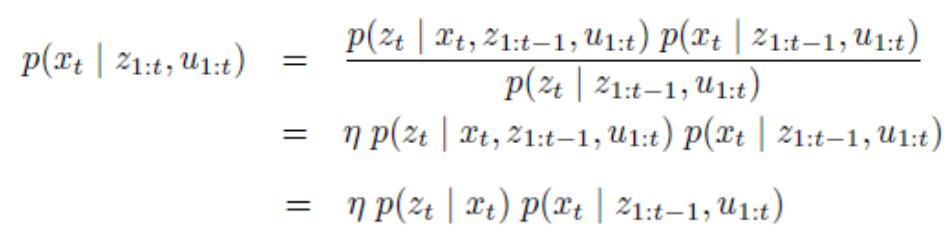
- 먼저 첫번째 줄에서 분모는 \(\eta\)로 치환되었습니다. 분모값은 확률을 1로 만들어 주기 위한 normalization 역할을 합니다.
- 두번째에서 세번째줄로 식이 유도될 때, \(p(z_{t} \vert x_{t}, z_{1:t-1}, u_{1:t}) = p(z_{t} \vert x_{t})\)로 간소화 될 수 있는 이유는
Markov Assumption에 따라서 조건부의 \(x_{t}\)가 \(z_{1:t-1}, u_{1:t}\)을 포함하기 때문입니다. - 이와 같이 식을 유도하였을 때, \(p(x_{t} \vert z_{1:t-1}, u_{1:t}) = \overline{bel}(x_{t})\) 이고 \(p(x_{t} \vert z_{1:t}, u_{1:t}) = bel(x_{t})\) 이므로 다음과 같이 식을 정리할 수 있습니다.
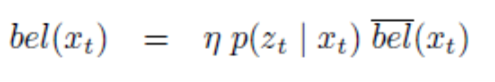
- 이 식을 Bayes Filter에 적용하면 다음과 같습니다.

- 이와 같은 방법으로 Bayes Filter의 measurement update (correction) 과정을 마칠 수 있습니다.
- 지금까지 살펴본 control update (prediction)과 measurement update(correction)을 통하여 \(t\) 시간에서의 Bayes Filter를 적용할 수 있습니다.
- 이 때 계산된 결과를 \(t + 1\) 시간에서의 Bayes Filter로 넘겨줌으로써 Recursive하게 Filter를 적용할 수 있습니다.
로봇 이동 예제를 통한 Bayes Filter 수식의 이해
- 앞에서 배운 수식을 간단한 로봇 이동 예제를 이용하여 적용해 보도록 하겠습니다.
- 첫번째 예제는 제어값이 없는 상태에서의 Bayes Filter 이고 두번째 예제는 제어값이 있는 상태에서의 Bayes Filter 예제입니다.
- 첫번째 예제에서는 앞에서 다룬 Bayes Filter 보다 조금 더 간단한 수식을 사용하고 이를 확장한 두번째 예제에서는 제어값, 센서값 모두를 사용하여 앞에서 다룬 Bayes Filter와 동일한 수식을 사용합니다.
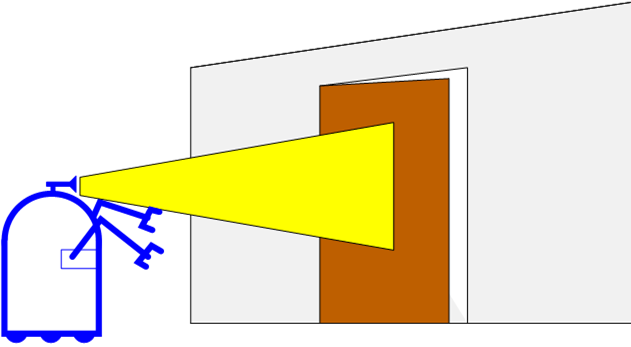
- 첫번째 예제에서 상태는 문이 열려 있음 / 닫혀 있음에 해당하고 센서값은 로봇이 문 앞으로 갔을 때, 센서 값으로 인지한 문의 상태 입니다.
state(x): open / closemeasurement(z): open / close
- Bayes Filter는 Bayes Theory를 이용합니다. Bayes Theory를 적용할 때, 반드시 필요한
prior,posterior,likelihood에 대한 정의는 아래와 같습니다. prior: \(p(\text{open})\) : 문이 열린 상태일 확률likelihood: \(p(z \vert \text{open})\) : 문이 열려 있있을 때, 센서 값의 상태가 \(z\) (open)일 확률로 실제 관측 가능한 값posterior: \(p(\text{open} \vert z)\) : 센서 값의 상태가 \(z\)(open)일 때, 문이 열린 상태일 확률 (posterior는 실제 관측하여 데이터 구축하는 것이 likelihood 경우 보다 어렵기 때문에 likelihood를 이용하여 posterior를 구합니다.)
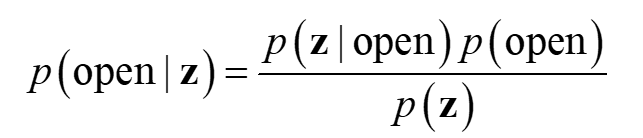
- 이 때, prior, likelihood는 다음을 따른다고 가정하겠습니다. 실제 문제에 적용할 때에도 likelihood는 구축된 사례나 데이터등을 이용하여 정의되어야 합니다.

- 먼저 초기 상태 (\(t = 0\))에서 문이 열렸거나 닫혀 있을 상태는 0.5로 동등한 상태라고 가정하겠습니다. (
prior) - 문이 열려 있는 상태에서 로봇이 문이 열렸다고 센서로 감지할 확률은 0.6, 문이 닫혔을 때, 센서로 문이 열렸다고 감지할 확률은 0.3 이라고 가정하겠습니다. (
likelihood) 실제 likelihood는 관측값들을 통하여 생성할 수 있습니다. - 구하고자 하는
posterior는 센서가 문이 열렸다고 감지하였을 때, 실제 문이 열렸을 확률 입니다. 위 식과 같이 total probability를 이용하여 \(t=1\)의posterior를 구할 수 있습니다.
- 다시 한번 설명 하면
Markov Assumption을 이용하여 그 다음 식인 \(t=2\)일 때의posterior를 추정할 수 있습니다.
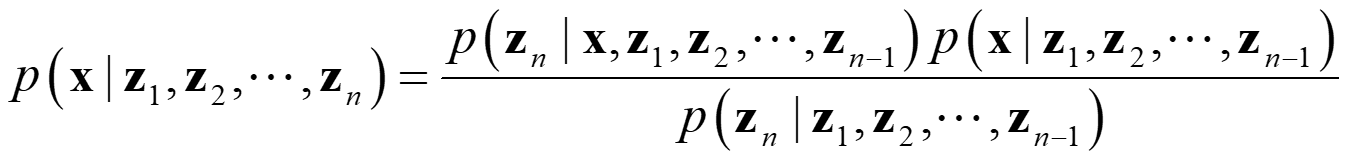
Markov Assumption은 위 식에서 \(z_{n}\)이 \(z_{1}, z_{2}, \cdots , z_{n-1}\)과 모두 독립이라는 가정을 두는 것입니다. 따라서 다음과 같이 식을 전개할 수 있습니다.
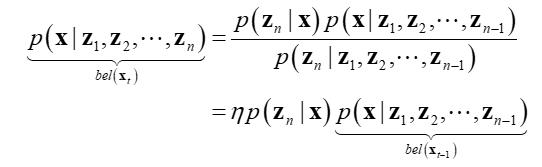
- \[\therefore \ \ bel(X_{t}) = p(X \vert Z_{1}, Z_{3}, \cdots , Z_{n}) = \eta \cdot p(Z_{n} \vert X)bel(X_{t-1})\]
- 앞에서 구한 \(\color{red}{p(\text{open} \vert z) = 0.67}\)은 \(t=2\)에서
prior로 사용됩니다. - 따라서 \(bel(x_{2})\) 구할 때, \(bel(x_{1}) = 0.67\)이 됩니다. 아래 식을 참조해 보겠습니다.

- 위 식에서는 \(t=2\)에서의
posterior에 대하여 구해봅니다. 이 때, 사용하는prior는 \(t=1\)에서 구한posterior가 됩니다. (빨간색 값을 참조) - likelihood에서 실제 문이 열렸을 때, 센서 또한 문이 열렸다고 감지할 확률이 0.5 보다 큰 0.6 이기 떄문에 재귀적으로 이 작업이 반복된다면 위 식의 파란색 값과 같이 점점 더 확률이 커지게 되는 것을 알 수 있습니다.
- 이번에는 제어값과 센서값이 모두 사용되는 상황의 예제에 대하여 살펴보도록 하겠습니다.
- \(X\) : 문이 열린 상태 / 닫힌 상태
- \(Z\) : 로봇 센서가 문이 열린 상태 / 닫힌 상태로 감지하는 상태
- \(U\) : 로봇이 문을 미는 상태 / 밀지 않는 상태
- 각 상태 \(X, Z, U\)가 위와 같이 정의되었을 때, 각 확률은 다음과 같습니다.

- 먼저 문이 열리거나 닫힌 초기값 상태는 각각 0.5로 가정하겠습니다.
- 먼저
센서값에 대한조건부 확률를 정의해 보도록 하겠습니다. - 변수는 센서값의 상태와 문이 열리고 닫힌 상태 2가지이므로 아래와 같이 총 4가지의 확률이 계산됩니다.
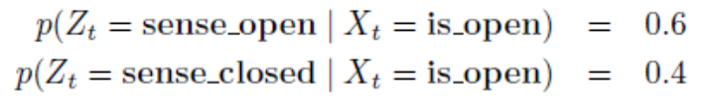
- 센서값의 확률은 문이 열려 있을 때, 센서도 문이 열렸다고 감지할 확률이 0.6이라고 가정합니다.
- 따라서 문이 열려 있을 때, 센서는 문이 닫혔다고 감지할 확률은 0.4로 판단합니다.
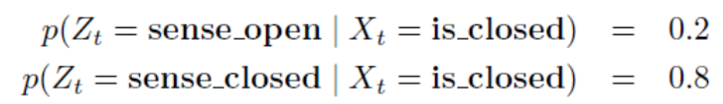
- 문이 닫혀 있을 때, 센서도 문이 닫혔다고 감지할 확률은 0.8이라고 가정합니다.
- 따라서 문이 닫혀 있을 때, 센서가 문이 열렸다고 감지할 확률은 0.2로 판단합니다.
- 그 다음으로
제어값에 대한조건부 확률을 가정해 보도록 하겠습니다. - 변수는 센서값의 상태, 문이 열리고 닫힌 상태 그리고 로봇이 문을 밀거나 밀지 않은 상태 총 3가지이므로 아래와 같이 총 8가지의 확률이 계산됩니다.
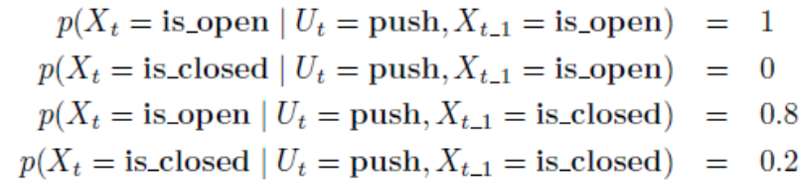
- 먼저 위 식은 로봇이 문을 미는 경우의 조건부 확률을 위 식과 같이 정의 하였습니다.

- 위 식은 로봇이 문을 밀지 않은 경우의 조건부 확률을 위 식과 같이 정의하였습니다.
- 지금부터 위에서 정의한 식을 이용하여 베이즈 필터를 전개해 보도록 하곘습니다.
- 각 시간 \(t\)에 대하여 상태 \(X_{t}\)는 \(t\) 시간의
제어값과센서값에 의하여 결정됩니다. - 먼저 \(X_{1}\)에서는
제어값은 아무 것도 하지 않음이고센서값은 open인 상태를 기준으로 식을 전개해 보겠습니다.
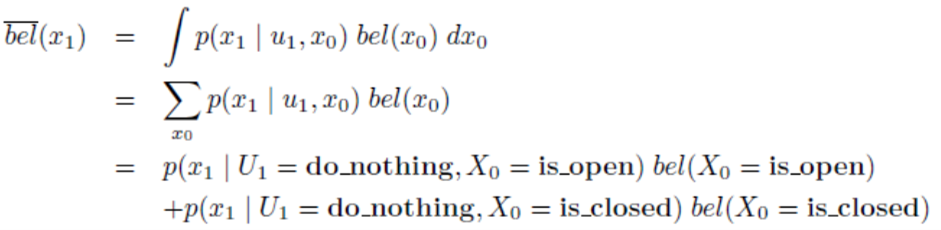
- 먼저 위 식은 문의 상태에 따른
제어값의 확률 분포를 반영한 식입니다. 제어값이 아무 것도 하지 않음으로 입력 되기 때문에 위 식과 같이control update(prediction)을 할 수 있습니다. - 위 식에서 실제 문이 열렸을 상태와 문이 닫혔을 상태를 분리하여 확률 값을 아래와 같이 계산해 보도록 하겠습니다.
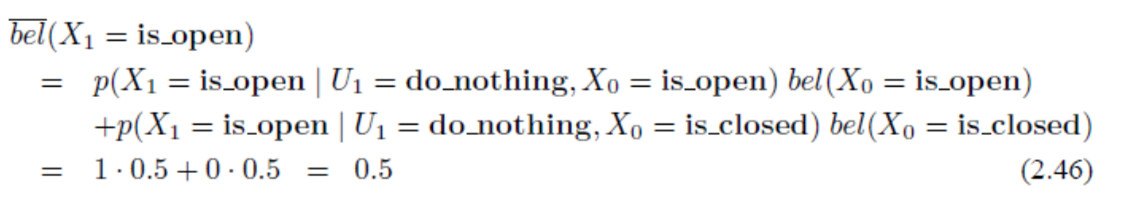
- 앞에서 가정한 확률 값에 따라 \(\overline{bel}(X_{1} = \text{is_open}) = 0.5\) 를 구할 수 있습니다.
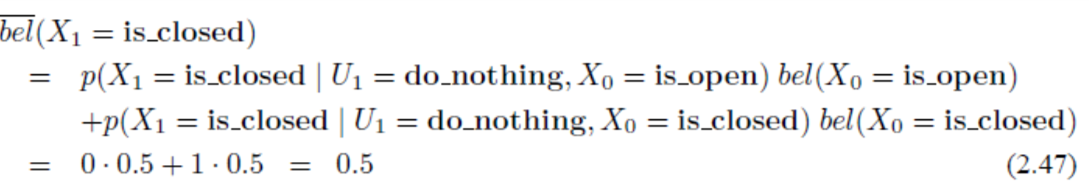
- 또한 \(\overline{bel}(X_{1} = \text{is_closed}) = 0.5\) 를 구할 수 있습니다.
- 따라서 문이 열렸을 때와 닫혔을 때의
control update(prediction)을 구할 수 있습니다.
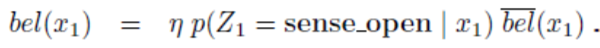
- 센서값은 open이라고 관측되었다고 가정하였으므로 다음과 같이 식을 전개할 수 있습니다.
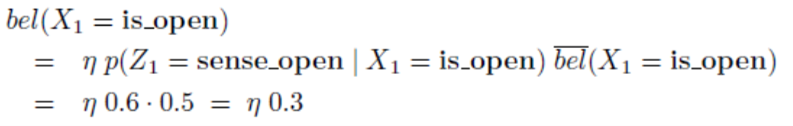
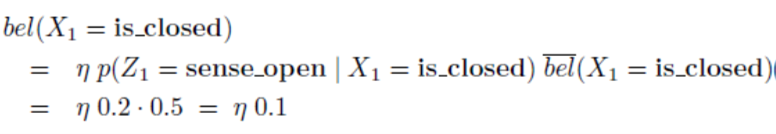
- 이 때 \(\eta\) 는 확률 값을 1로 만들기 위해 필요한 값으로 다음과 같이 구할 수 있습니다.
- \[\eta = (0.3 + 0.1)^{-1} = 2.5\]
- \[bel(X_{1} = \text{is_open}) = \eta * 0.3 = 2.5 * 0.3 = 0.75\]
- \[bel(X_{1} = \text{is_closed}) = \eta * 0.1 = 2.5 * 0.1 = 0.25\]

- 따라서
센서값은 open이고제어값은 아무 것도 하지 않음 상태일 때, 위와 같이 확률 값을 계산할 수 있습니다.
- 이번에는 앞의 계산 결과를 이용하여 \(X_{2}\)의 식을 전개해 보겠습니다.
센서값은 open이고제어값은 문을 미는상태일 때, 확률 값을 계산해 보도록 하겠습니다.
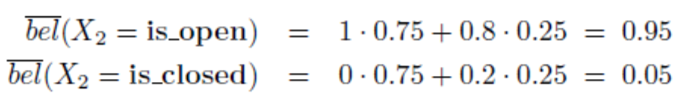
- \[\begin{align} \overline{bel}(X_{2} = \text{is_open}) &= p(X_{2} = \text{is_open} \vert U_{2} = \text{push}, X_{1} = \text{is_open})bel(X_{1} = \text{is_open}) \\ &+ p(X_{2} = \text{is_open} \vert U_{2} = \text{push}, X_{1} = \text{is_closed})bel(X_{1} = \text{is_closed}) \\ &= 1 * 0.75 + 0.8 * 0.25 = 0.95 \end{align}\]
- \[\begin{align} \overline{bel}(X_{2} = \text{is_closed}) &= p(X_{2} = \text{is_closed} \vert U_{2} = \text{push}, X_{1} = \text{is_open})bel(X_{1} = \text{is_open}) \\ &+ p(X_{2} = \text{is_closed} \vert U_{2} = \text{push}, X_{1} = \text{is_closed})bel(X_{1} = \text{is_closed}) \\ &= 0 * 0.75 + 0.2 * 0.25 = 0.05 \end{align}\]
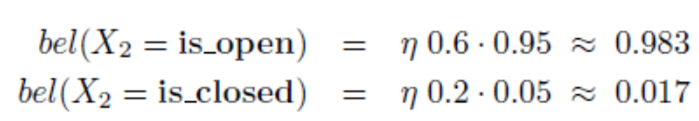
- \[bel(X_{2} = \text{is_open}) = \eta \cdot p(Z_{2} = \text{sense_open} \vert X_{2} = \text{is_open}) \overline{bel}(X_{2} = \text{is_open}) = \eta \cdot 0.6 \cdot 0.95 = \eta \cdot 0.57\]
- \[bel(X_{2} = \text{is_closed}) = \eta \cdot p(Z_{2} = \text{sense_open} \vert X_{2} = \text{is_closed}) \overline{bel}(X_{2} = \text{is_closed}) = \eta \cdot 0.2 \cdot 0.05 = \eta \cdot 0.01\]
- \[(0.57 + 0.01)^{-1} \approx 1.724\]
- \[bel(X_{2} = \text{is_open}) = \eta \cdot 0.57 \approx 1.724 \cdot 0.57 = 0.983\]
- \[bel(X_{2} = \text{is_closed}) = \eta \cdot 0.01 \approx 1.724 \cdot 0.01 = 0.017\]
- 따라서 위와 같이 \(X_{2}\)에서의 위치 상태를 제어값과 센서값을 이용하여 추정할 수 있습니다.
- 위 프로세스들을 관찰해 보면 이전 상태와 제어값을 이용하여 현재 상태를 추정하고 센서값을 이용하여 보정하는 작업을 매 시간 별 진행합니다.
- 따라서 연산에 사용되는 제어값과 센서값에 의하여 상태는 계속 변하게 됩니다. 간혹 제어값 또는 센서값이 부정확하게 들어온다고 하더라도 이전 상태를 이용하여 연산되기 때문에 필터의 기능이 작용 되어 급격하게 값이 변화하지는 않습니다. 이러한 원리로 Bayes Filter가 적용됩니다.
자동차 이동 예제를 이용한 Bayes Filter 수식의 이해
- 이번에는 자동차 이동 예제를 통하여 Bayes Filter 수식을 살펴보도록 하겠습니다. 이 예제는 직전 자동차의 위치 \(bel(x_{t-1})\) 를 기준으로 현재 자동차의 위치 \(bel(x_{t})\)를 추정하는 예제입니다.
- 추정하는 방법은 \(bel(x_{t-1})\)를 기준으로 현재 시간의 제어(\(u_t\))를 반영하고 현재 시간의 센서값(\(u_t\))을 통하여 보정하는 작업을
베이즈 필터를 이용하여 적용해 보겠습니다.
- 먼저 이전 시간 \(t - 1\)까지의 자차의 위치는 다음과 같다고 가정하겠습니다.
- \[bel(x_{t-1}=i) = \begin{cases} i=-1 : 0.2 \\ i=0: 0.7 \\ i=1 : 0.1\end{cases}\]


- 위에서 작업한 과정은 베에즈 필터 식의 ①에 해당합니다.
- 위 상태에서 현재 시간 \(t\)의 제어값인 \(u_{t} = +3\) 즉, 오른쪽으로 3칸 이동을 반영해 보도록 하겠습니다. 이 때, 제어값에 대한 노이즈가 존재하므로 이 또한 확률 분포로 나타내면 다음과 같습니다.
- \[p(u_{t}=i) = \begin{cases} i=2 : 0.2 \\ i=3 : 0.6 \\ i=4 : 0.2 \end{cases}\]
- 직전 상태에서 현재 시간에 입력 받은 제어값을 반영할 때, 모든 경우의 확률 분포를 반영해야 합니다.
- 즉, 직전 상태 \(x_{t-1}\)의 -1, 0, 1 각각에서 제어값을 입력 받았을 때의 확률 분포를 구해야 합니다.
- 먼저 \(bel(x_{t-1} = -1)\)의 상태부터 고려해 보도록 하겠습니다.
- 아래 그림의 자동차가 투명할수록 확률은 0에 가깝고 불투명할수록 높은 확률을 가집니다.
- \[bel(x_{t-1} = -1)p(x_t=1 \vert u_t=2, x_{t-1} = -1)=0.2\times0.2=0.04 \tag{1}\]
- \[bel(x_{t-1} = -1)p(x_t=2 \vert u_t=3, x_{t-1} = -1)=0.2\times0.6=0.12 \tag{2}\]
- \[bel(x_{t-1} = -1)p(x_t=3 \vert u_t=4, x_{t-1} = -1)=0.2\times0.2=0.04 \tag{3}\]
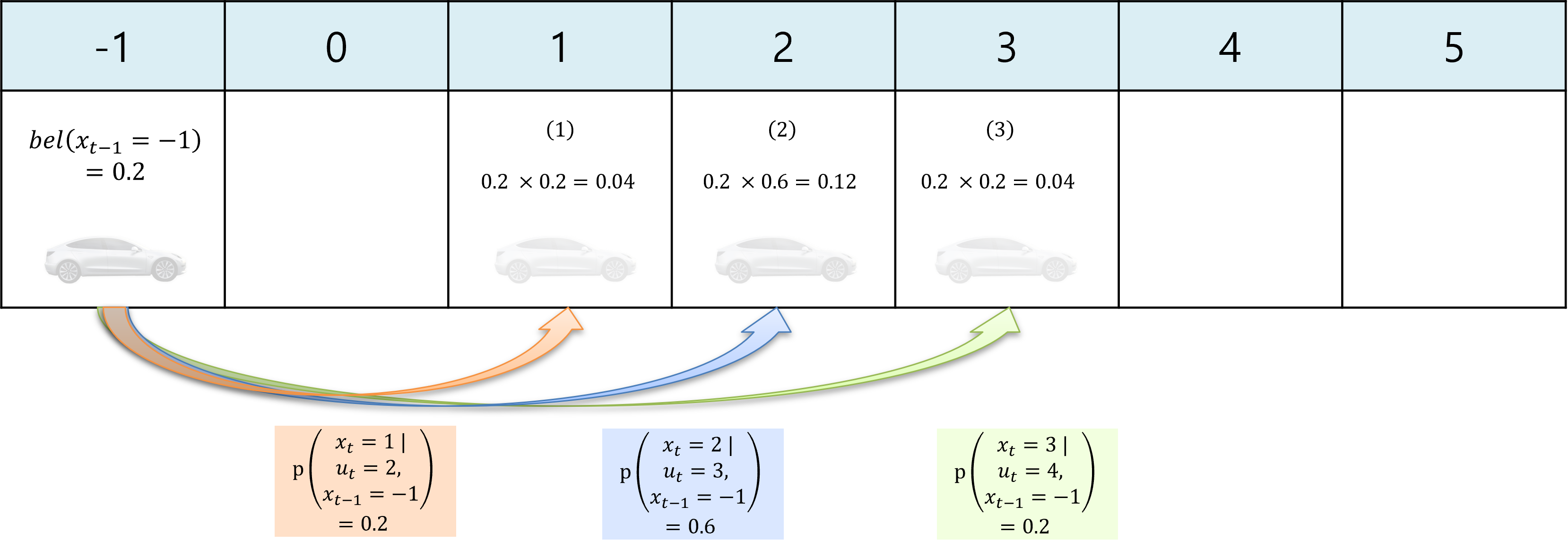
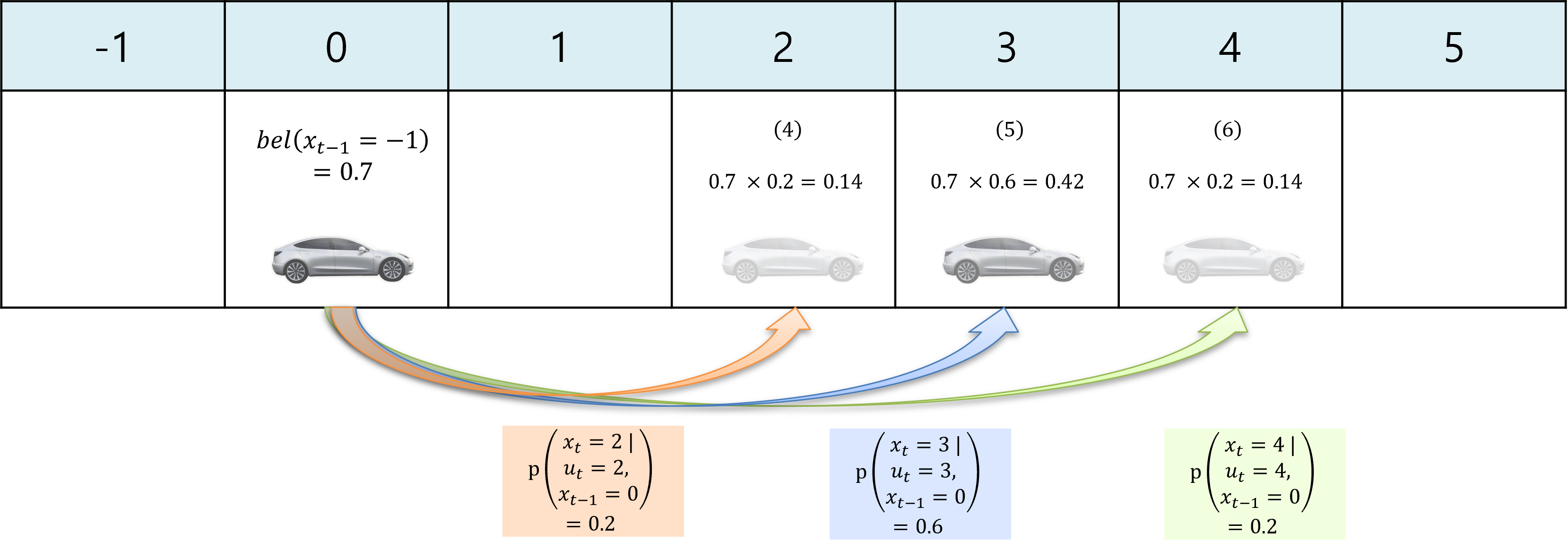
- 그 다음으로 \(bel(x_{t-1} = 0)\)상태를 고려해 보도록 하겠습니다.
- \[bel(x_{t-1} = 0)p(x_t=2 \vert u_t=2, x_{t-1} = 0)=0.7\times0.2=0.14 \tag{4}\]
- \[bel(x_{t-1} = 0)p(x_t=3 \vert u_t=3, x_{t-1} = 0)=0.7\times0.6=0.42 \tag{5}\]
- \[bel(x_{t-1} = 0)p(x_t=4 \vert u_t=4, x_{t-1} = 0)=0.7\times0.2=0.14 \tag{6}\]
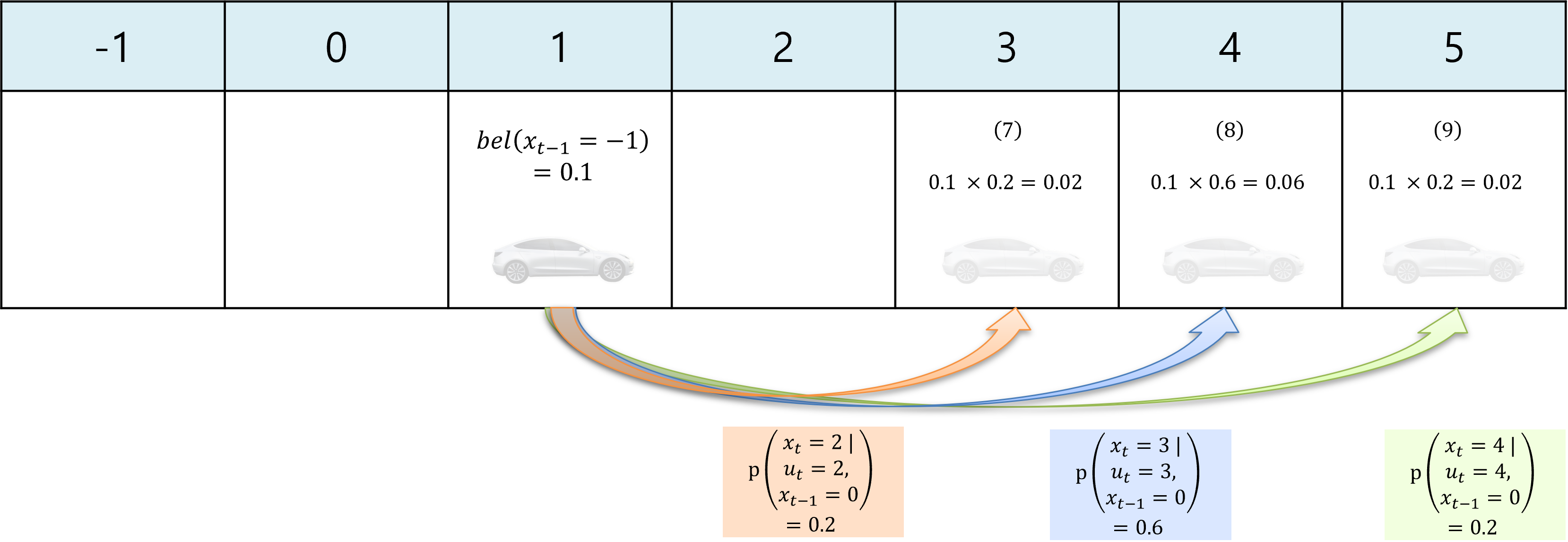
- 마지막으로 \(bel(x_{t-1} = 1)\) 상태를 고려해 보도록 하겠습니다.
- \[bel(x_{t-1} = 1)p(x_t=3 \vert u_t=2, x_{t-1} = 1)=0.1\times0.2=0.02 \tag{7}\]
- \[bel(x_{t-1} = 1)p(x_t=4 \vert u_t=3, x_{t-1} = 1)=0.1\times0.6=0.06 \tag{8}\]
- \[bel(x_{t-1} = 1)p(x_t=5 \vert u_t=4, x_{t-1} = 1)=0.1\times0.2=0.02 \tag{9}\]
- 지금까지 살펴본 \(bel(x_{t-1})\) 을 모두 검토하였을 때, 아래와 같이 각 위치에서는 \(\overline{bel(x_{t})}\) 를 구할 수 있습니다. 앞에서 살펴본 바와 같이 bar 형태는 prediction에 해당합니다.
- \[\overline{bel}(x_{t} = 1) = 0.04 (\text{eq. (1)}) = 0.04\]
- \[\overline{bel}(x_{t} = 2) = 0.12 (\text{eq. (2)}) + 0.14 (\text{eq. (4)}) = 0.26\]
- \[\overline{bel}(x_{t} = 3) = 0.04 (\text{eq. (3)}) + 0.42 (\text{eq. (5)}) + 0.02 (\text{eq. (7)}) = 0.48\]
- \[\overline{bel}(x_{t} = 4) = 0.14 (\text{eq. (6)}) + 0.06 (\text{eq. (8)}) = 0.20\]
- \[\overline{bel}(x_{t} = 5) = 0.02 (\text{eq. (9)}) = 0.02\]

-
위 식에서 \(\sum_{i=1}^{5} \overline{bel}(x_{t} = i) = 1\) 을 만족함으로 확률의 합은 1인것을 확인할 수 있습니다.
-
이와 같은 방법으로 직전 위치와 제어값을 이용하여 현재 위치를 추정할 수 있습니다.

- 지금 작업한 과정은 베에즈 필터 식의 ②, ③에 해당합니다.
- 이번에는 앞에서 추정한 값을 보정(correction)하기 위하여 GPS 센서 값을 사용하겠습니다. 글 앞에서 다룬것 처럼 센서값은 \(z_{t}\)로 표현하겠습니다.
- GPS를 이용하여 얻은 \(t\) 시간의 현재 위치값 \(z_{t}\) 가 다음과 같다고 가정해 보겠습니다.
- \[p(z_{t} =i \vert x_{t} ) = \begin{cases} i = 1 : 0.05 \\ i=2 : 0.20 \\ i=3 : 0.50 \\i=4 : 0.20 \\ i=5 : 0.05\end{cases}\]
- 이 때, 확률 분포는 다음과 같습니다.
- \[p(z_t = 1 \vert x_{t} ) \overline{bel}(x_t = 1) = 0.05 \times 0.04 = 0.002\]
- \[p(z_t = 2 \vert x_{t} ) \overline{bel}(x_t = 2) = 0.20 \times 0.26 = 0.052\]
- \[p(z_t = 3 \vert x_{t} ) \overline{bel}(x_t = 3) = 0.50 \times 0.48 = 0.24\]
- \[p(z_t = 4 \vert x_{t} ) \overline{bel}(x_t = 4) = 0.20 \times 0.20 = 0.04\]
- \[p(z_t = 5 \vert x_{t} ) \overline{bel}(x_t = 5) = 0.05 \times 0.02 = 0.001\]

- 지금 작업한 과정은 베에즈 필터 식의 ④에 해당합니다.
- 위 값들을 모두 더하면 1이 되지 않으므로 normalization을 하기 위하여 \(\eta\)를 곱해주어야 합니다. \(\eta\)는 위 값을 모두 더한값의 역수가 됩니다.
- \[\eta = 1 / (0.002 + 0.052 + 0.24 + 0.04 + 0.001) = 2.9851\]
- \[bel(x_{t} = 1) = \eta p(z_t = 1 \vert x_{t} ) \overline{bel}(x_t = 1) = 2.9851 \times 0.05 \times 0.04 = 0.005970149\]
- \[bel(x_{t} = 2) = \eta p(z_t = 2 \vert x_{t} ) \overline{bel}(x_t = 2) = 2.9851 \times 0.20 \times 0.26 = 0.155223881\]
- \[bel(x_{t} = 3) = \eta p(z_t = 3 \vert x_{t} ) \overline{bel}(x_t = 3) = 2.9851 \times 0.50 \times 0.48 = 0.71641791\]
- \[bel(x_{t} = 4) = \eta p(z_t = 4 \vert x_{t} ) \overline{bel}(x_t = 4) = 2.9851 \times 0.20 \times 0.20 = 0.119402985\]
- \[bel(x_{t} = 5) = \eta p(z_t = 5 \vert x_{t} ) \overline{bel}(x_t = 5) = 2.9851 \times 0.05 \times 0.02 = 0.002985075\]

- 위 값을 모두 합하면 1이 되므로 확률로 나타낼 수 있습니다. 뿐만 아니라 예측값을 센서값으로 보정하여 자동차의 위치를 파악하는 데 더 용이해 졌습니다.

- 마지막으로 작업한 과정은 베에즈 필터 식의 ⑤에 해당합니다.
Bayes Filter의 한계와 개선 방법
- 이 글의 도입부에서 소개드린 바와 같이 Bayes Filter는 Kalman Filter와 Particle Filter 개념의 기초가 된다고 말씀드렸습니다.
- 반대로 말하면 Kalman Filter와 Particle Filter는 Bayes Filter가 가지는 한계점으로 인하여 탄생한 것이라고 말할 수 있습니다.
- 지금까지 이 글을 살펴보면서 확인한 바로는 Bayes Filter의 큰 단점이 없는 것 처럼 보입니다. 하지만 굉장히 큰 단점이 있는 그것은 바로
prediction할 때 사용되는적분연산 입니다.

- 위 Bayes Filter 식을 살펴보면 Prediction 부분에 적분 연산이 있습니다. 적분 연산은 경우에 따라서 굉장히 연산이 복잡하거나 연산량이 많을 수 있고 심지어 적분이 불가능한 경우 까지 발생합니다.
- 다행히도 Discrete Case인 경우 단순히 \(\sum\)으로 합 연산을 하면 되지만 Continuous Case인 경우 반드시 적분 연산을 해야 하기 때문에 계산하는 데 문제가 발생할 수 있습니다.
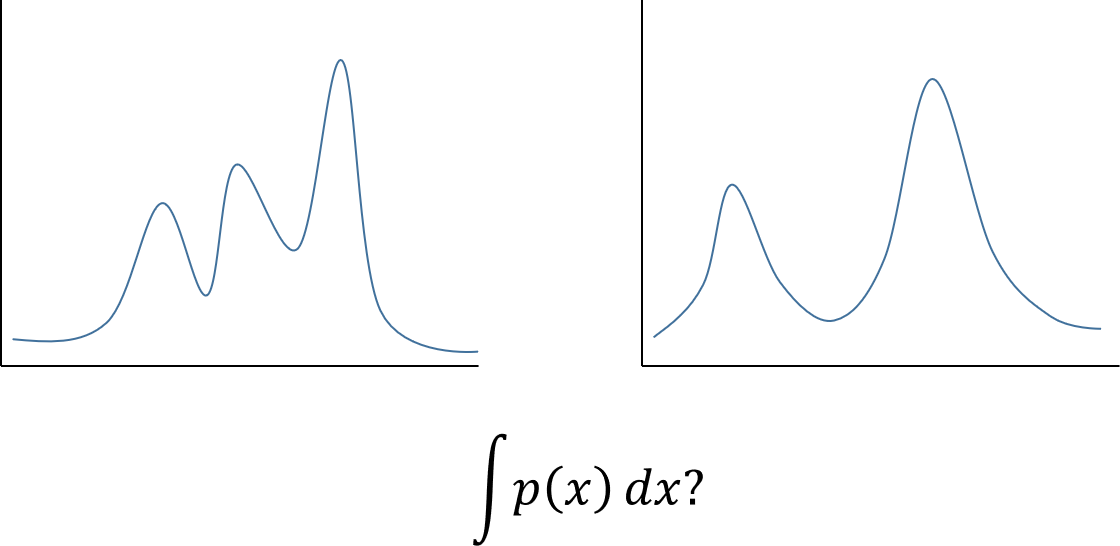
- 예를 들어 위 그림과 같은 multimodal 형태의 곡선을 적분하는 것은 생각보다 쉽지 않을 수 있습니다. 계산 과정도 복잡하여 어플리케이션에서 사용하기 어려울 수도 있습니다.
- 이와 같은 문제를 해결하기 위하여 크게 2가지 방법이 있습니다.
- 첫번째가 적분이 되지 않는 식을 적분하는 대신
Monte Carlo Integration이란 방법의 랜덤 샘플링 방식을 통하여 근사화 하는 방법이 있습니다. 이 방법을 이용한 Bayes Filter가Particle Filter가 됩니다. - 랜덤 샘플링 방식을 통하여 Bayes Filter를 개선하는
Particle Filter에 대한 이해가 필요하시면 다음 링크를 참조하시기 바랍니다.
- 두번째 방법은 더 간단합니다. 적분이 되는 식만 사용하는 컨셉입니다. 적분을 쉽게 할 수 있으면서 적분이 안되는 식을 근사화 하여 사용할 수 있는 확률 분포가 있을까요? 네 있습니다. 바로
가우시안 (정규) 분포입니다.
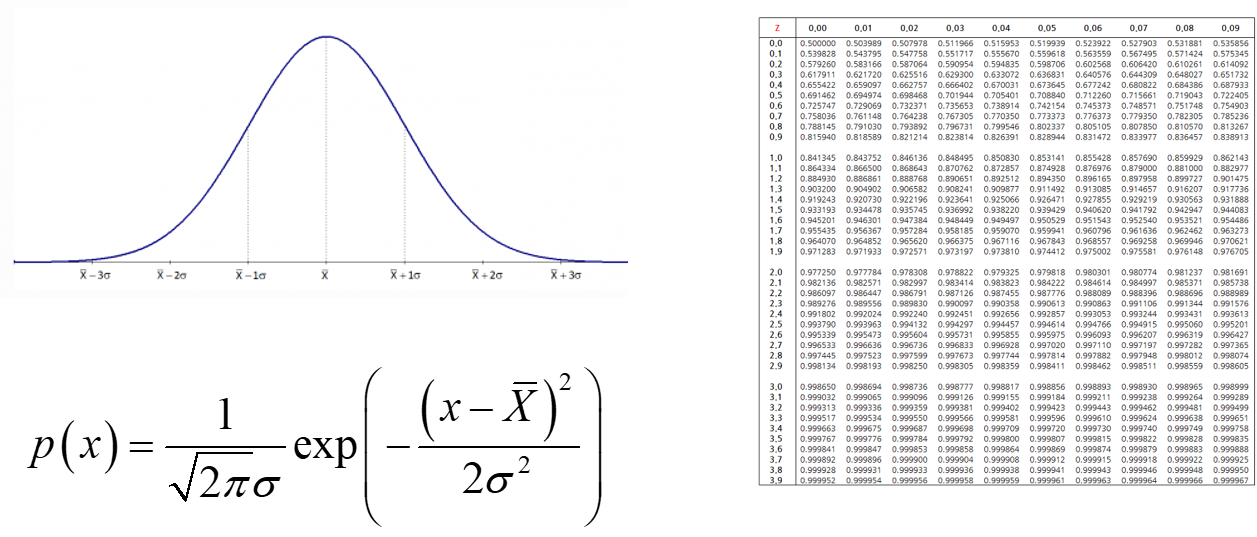
- 가우시안 분포는 위 그림과 같이 이미 적분이 다 되어 있어서 어느 영역이든지 적분이 가능합니다.
- 심지어 적분 테이블 까지 마련되어 있을 정도입니다. 뿐만 아니라 파라미터도
평균과표준편차만 있어서 다루기가 쉽습니다. - Bayes Filter의 제어값과 센서값의 노이즈가 정규 분포를 따른다고 가정하고 특히, 노이즈의 평균은 0, 표준편차는 \(\sigma\)를 따른다고 가정하면 이 문제는 굉장히 쉬워집니다.
- 이와 같이 Bayes Filter에서 상태 방정식의 분포 및 노이즈가
가우시안 분포를 따르는 Filter를Kalman Filter라고 합니다. - Bayes Filter가 다 이해가 되셨다면 다음 링크의 Linear Kalman Filter를 학습해 보시길 추천드립니다.