자율주행에서의 Localization과 Tracking

이번 글에서는 간단하게 자율주행에서의 Localization과 Tracking의 차이에 대하여 알아보도록 하겠습니다.
먼저 Localization 문제는 자차의 키네마틱 정보를 인식하는데 이 때, 센서값과 컨트롤 입력값을 사용하는 케이스를 뜻합니다.
이 때 사용하는 센서값과 컨트롤 입력에 노이즈가 발생할 수 있다는 것을 전제로 하며 이 센서값과 컨트롤 입력값을 이용하여 더 정확하게 자차의 키네마틱 정보를 예측하는 것이 목표이고 이를 재귀적으로 구현합니다.

반면 Tracking 문제는 위의 Localization 문제에서 정보 하나가 빠지게 됩니다. 바로 컨트롤 입력값 입니다.
Tracking이라고 하면 자차의 상태가 아니라 주변 차 또는 자차 이외의 무언가의 상태를 추정하는 것이기 때문에 Localization 때와 같이 컨트롤 입력값을 받을 수 없습니다.
예를 들어 Localization은 컨트롤 입력값을 받기 때문에 예를들어 Accelerator 페달을 얼만큼 밟았는 지, 휠을 몇 도 움직였는 지 등을 알 수 있습니다.
반면 Tracking에서는 컨트롤 입력값이 빠지기 때문에 Localization에 비해 다소 문제가 어려워 집니다.

\[p(x_{t} \vert x_{0:t-1}, z_{1:t-1}, u_{1:t}) = p(x_{t} \vert x_{t-1}, u_{t})\]

위 식의 좌변은 처음 시점 부터 직전 시점(t-1)의 위치와 센서값 그리고 컨트롤 입력값을 이용하여 현재 시점 t에서의 위치를 추정하는 확률식입니다.
우변을 보면 조건부에서 위치값인 \(x_{t-1}\) 이외에 \(x_{0}\) ~ \(x_{t-2}\)까지는 모두 생략되었는데 그 이유는 독립이라는 가정하에 직전 데이터인 \(x_{t-1}\)와 \(u_{t}\)를 제외하고 모두 생략하였습니다. (물론 상황에 따라 종속적인 경우가 있다면 종속적이라 생각되는 케이스는 추가로 곱해주어도 상관없습니다.)
이런 성질을 Markov Property 라고 합니다. 즉 현재 상태는 직전 상태에 영향을 받는다는 가정을 통하여 문제를 단순화 시킨 것입니다.
- 즉, \(P(x_{t} \vert x_{0}, x_{1}, ..., x_{t-1} ) \approx P(x_{t} \vert x_{t-1})\)로 가정하는 것입니다.
- 간단하게 생각하면 직전 상태인 \(P(x_{t-1})\)은 그 이전의 모든 상태를 함축하고 있다고 보는 것입니다.

위 식은 앞에서 구한 \(x_{t}\)를 기반으로 센서값인 \(z_{t}\)를 업데이트 합니다.
필요한 \(x_{t}\)와 \(z_{t}\)를 구하였기 때문에, 최종적으로 믿고 싶은 위치(\(\text{bel}\)은 belief를 뜻함)인 \(bel(x_{t})\)는 다음과 식과 같습니다.

위 식에서 \(bel(x_{t})\)가 나타내는 것은 현재 상태를 나타냅니다. 단, 이 때 조건은 알고리즘이 시작된 처음부터 현재 까지의 모든 센서 데이터 및 컨트롤 입력 데이터가 있다는 것입니다. 따라서 \(bel(x_{t}) = p(x_{t} \vert z_{1:t}, u_{1:t})\)는 알고리즘 시작에서 부터 현재 까지의 모든 센서 및 컨트롤 입력 데이터를 기준으로 현재 상태를 찾아내는 것을 뜻합니다.

위에서 다룬 내용은 Localization에 관련된 내용이었습니다. 그러면 Localization과 Tracking의 차이는 컨트롤 입력값을 직접적으로 받는 지 아닌지이므로 위에서 다룬 식에서 \(u\)만 지우면 Tracking 문제로 변환됩니다.

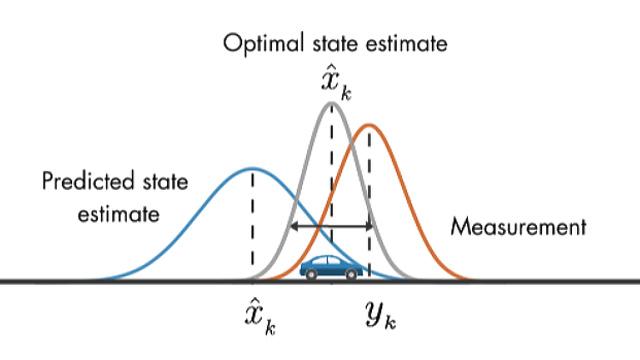
최적 상태 추정을 위해 사용되는 칼만 필터에서 Contorl Matrix와 Control Input이 있습니다.
Localization 문제를 풀 때에는 주어진 Control Input이 있기 때문에 이 값이 존재하지만, Tracking 문제에서는 이 값이 존재하지 않으므로 생략됩니다.
따라서 칼만 필터에서의 Tracking에서는 Control Input이 명시되지 않기 때문에 따로 입력되지는 않지만 그만큼 Control Input에 대한 state variance를 어떻게 선정하는 지가 상당히 중요해집니다.