상태 방정식 (state equation)
2020, Feb 01
- 최적 상태를 추적하기 위하여 칼만 필터와 같은 estimator를 사용할 때, 모델링을 하기 위하여 상태 방정식 (state equation)을 작성할 필요가 있습니다.
- 이번 글에서는 나름 쉬운(?) 상태 방정식 하나를 예를 들어 상태 방정식을 어떻게 작성하는 지 살펴보겠습니다.
- 먼저 2가지 용어에 대하여 간략하게 정의하고 진행 하겠습니다. 첫번째로
상태 방정식 (state equation)이란 이전의 상태(ex. 위치)와 현재 상태 사이 간의 관계를 나타냅니다. 두번째로측정 방정식(measurement equation)이란 현재 상태와 센서 데이터 사이의 관계를 뜻합니다. - 이 글에서 다루는 상태는 1차원에서 직선으로 움직이는 어떤 물체의 움직임입니다.
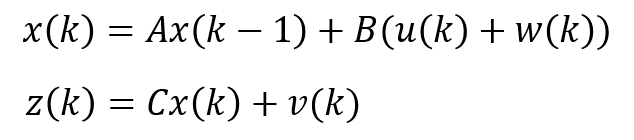
- 이 글에서 최종적으로 살펴볼 상태 방정식은 위와 같습니다.
- 바로 보면 이해가 안되므로 각 성분에 대해서 살펴보고 다시 이 식을 살펴보도록 하겠습니다.

- 먼저 각 식에 들어가 있는 모든 성분의 의미를 분석해 보면 위와 같습니다.
- 여기서 \(k\)는 몇 번째 step인 지에 해당합니다.
- \(x(k)\)는 k번째 step의 물체의 위치 상태에 해당합니다.
- \(\dot{x}(k)\)는 k번째의 step의 물체의 속도에 해당합니다.
- \(\ddot{x}(k)\)는 k번째의 step의 물체의 가속도에 해당합니다.
- \(T\)는 각 step 간 시간 간격을 뜻합니다.
- 그러면 첫번째 식부터 살펴보도록 하겠습니다.
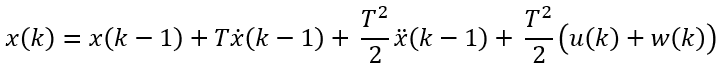
- 이 식은 이전 스텝 (k-1)의 위치 상태인 \(x(k-1)\)에 이전 스텝 (k-1)과 현재 스텝의 시간 간격(\(T\))에 이전 스텝의 속도(\(\dot{x}(k-1)\))를 곱한 값을 더하여 현재 위치를 추정합니다. 이것은 이동 거리 = 속도 * 시간을 이용한 것입니다. 이것은 다음 식을 반영한 것입니다.
- \[T\dot{x}(k-1)\]
- 이 때, 이전 스텝의 가속도를 이용하여 위치 상태를 좀 더 정확하게 추정할 수 있습니다. 이것은 1/2 * 가속도 * 시간^2을 이용하는 것입니다.
- \[\frac{T^{2}}{2}\ddot{x}(k-1)\]
- 마지막으로 현재 스텝에서 주어지는
제어 입력까지 추가하여 현재 위치를 추정할 수 있습니다. 제어 입력은 Localization 문제에서는 주어질 수 있으나 Tracking 문제에서는 알 수 없는 한계가 있습니다. 관련 내용은 이 링크를 살펴보시길 바랍니다.- control input이 주어졌다고 하였을 때, 이 값은 \(u(k)\)로 나타내겠습니다. 위 식에서는 이번 스텝에서 추가로 입력된 가속도라고 생각하시면 됩니다.
- 그러면 여기서 \(w(k)\)는 무엇일까요? 바로 이
제어 입력의noise입니다. - 위 물체가 자동차라고 하였을 때, 가속도를 주기 위해 엑셀을 밟아야 하는데 정확히 \(u(k)\) 만큼의 가속도를 줄 정도로 엑셀을 밟는 것은 사실 매우 어렵습니다. 예를 들어 내가 5m 이동하겠다고 마음 먹고 이동하는데, 정확히 5m 이동 하기는 어렵습니다. 5m에 최대한 가깝게 이동하려고 한다고 하더라도 오차가 발생하게 되는데 이 오차가 노이즈 입니다. 따라서 이런
제어 입력에는noise가 발생하는 데 이 노이즈를 고려해 주어야 하기 때문에 \(w(k)\)를 같이 고려해 주어야 합니다.
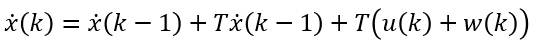
- 다음은 속도에 대한 식을 다루어 보겠습니다. 위 식의 각 항의 의미는 앞에서 다 다루었기 때문에 생략하겠습니다.
- 속도 = 현재 속도 + 가속도 * 시간의 물리 법칙을 따르기 때문에 위 식과 같이 적을 수 있습니다.
- 물론 앞에서 다루었듯이 control input에 대한 노이즈 까지 같이 고려하였습니다.
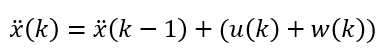
- 마지막으로 가속도에 대한 식이 위와 같습니다.
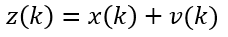
- 위 식에서 \(z(k)\)는 위치를 가리키는 센서 데이터를 나타냅니다.
- 따라서 위 관계 식은 앞에서 언급한 측정 방정식 (measurement equation)에 해당합니다.
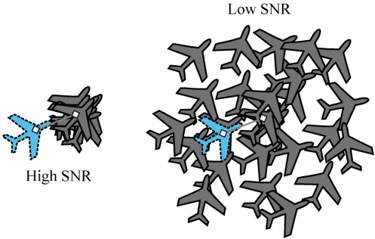
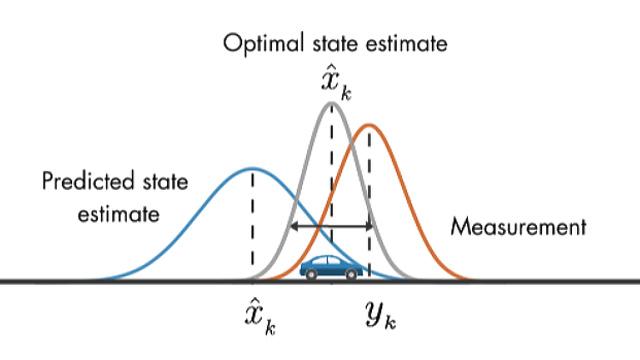
- 측정 방정식에서도 상태 방정식과 같이 노이즈 \(v(k)\)가 존재 합니다. 이 노이즈는 센서 자체의 노이즈(분산)과 같습니다. 위 그림과 같이 센서의 노이즈가 작으면 왼쪽과 같이 물체를 인식한 분포가 좁은 영역에 겹쳐져 있고 이는 노이즈(분산)이 작다고 말할 수 있습니다. 반면 오른쪽 그림에서는 노이즈(분산)이 커서 센서가 물체를 인식한 영역이 굉장히 넓게 나타납니다. 즉, 물체의 위치를 정확히 파악하기 어려워집니다. 이 노이즈 때문에 항상 \(z(k) = x(k)\)일 수 없고 오차가 발생하게 됩니다.
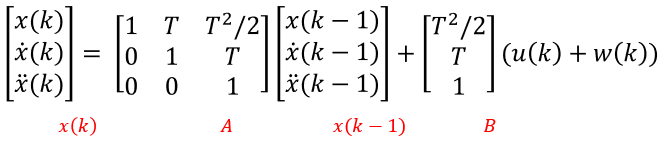
- 앞에서 다룬 식을 행렬로 묶으면 위와 같이 묶을 수 있습니다. 여기서 \(A\) 행렬을
state matrix라고 부릅니다. state equation에서 state를 모델링 할 때 핵심이 되는 행렬입니다. - 그리고 \(B\) 행렬을
control matrix라고 합니다. control input을 어떻게 줄 지에 대한 정의를 내려주기 때문입니다.
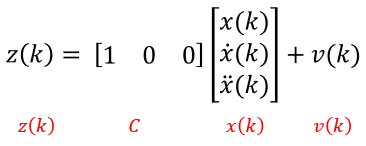
- 위 식의 \(C\) 행렬을
transition matrix라고 합니다. 이 행렬은 상태 추정식에 존재하는 차원 3개(위치, 속도, 가속도)를 센서 데이터의 1개 차원(위치)과 맞추어 줍니다. 일반적으로 모델링한 식의 차원의 수가 더 많고 센서 데이터의 차원의 수가 더 작으므로 높은 차원을 낮은 차원으로 매핑 하는게 쉬우므로 모델링 식의 차원을 센서 데이터의 차원으로 맞춰줍니다. - 앞에서 세운 식을 간략하게 표시하면 다음과 같습니다. 이 식이 상태방정식의 최종입니다.
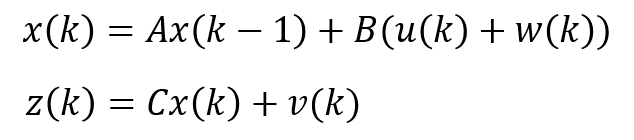
- 지금까지
상태 방정식\(x(k)\)와 추가적인측정 방정식에 \(z(k)\)에 대하여 알아보았습니다. - 앞에서 설명한 바와 같이 상태 방정식에서 제어 입력에 대한 노이즈는 \(w(k)\)로 표현하였고 측정 방정식에서 측정값에 대한 노이즈는 \(v(k)\)로 표현하였습니다.
- 이 값은 Localization과 Tracking 문제를 모델링 할 때, 굉장히 중요한 역할을 합니다. 특히 Tracking 문제에서 더 큰 역할을 합니다.
- 먼저 Localization과 Tracking 문제에 동일한 역할을 하는 측정 방정식의 노이즈는 센서값의 노이즈에 해당합니다. 따라서 이 노이즈는 실제 센서가 가지는 오차 범위를 반영하는 것이 합당합니다. 또는 센서 값에 높은 가중치를 주고 싶다면 \(v(k)\)를 0에 가깝게 설정하여 \(x(k) \approx z(k)\)로 만들 수 있습니다.
- 반면 Localization과 Tracking 문제에서 상태 방정식의 제어 입력값의 관점은 조금 다릅니다. Localization 문제에서는 제어 입력이 입력되는 반면에 Tracking 문제에서는 제어 입력이 주어지지 않습니다. 이 점이 두 문제의 차이점 입니다.
- 따라서 Localization은 제어 입력이 주어질 때, 그 값에 대한 노이즈를 입력하면 됩니다. 측정값 처럼 수치적으로 정확하게 알 수는 없겠지만 개념으로 이 값을 튜닝할 수 있습니다. 예를 들어 위 예제에서 고속으로 이동할 때가 저속으로 이동할 때 보다 노이즈가 더 유입될 가능성이 있기 때문에 고속인 경우 더 큰 노이즈 \(w(k)\)를 사용할 수 있습니다.
- 반면 Tracking 문제에서는 제어 입력이 주어지지 않습니다. 마치 3자의 입장에서 관측을 통하여 상태를 추정해야 합니다. 따라서 제어 입력 없이 노이즈 만으로 제어 입력을 대변할 수 있도록 정교하게 모델링해야 합니다. 따라서 Localization과 유사한 방법으로 노이즈 \(w(k)\)를 설정해야 하지만 상태 방정식의 성능이 잘 나올 수 있도록 파라미터 튜닝의 작업이 많이 필요합니다. 즉, Tracking 문제가 Localization 문제 보다 훨씬 어렵다고 말할 수 있습니다.