Attention 메커니즘의 이해

deep learning 관련 글 목차

참조 : Neural Machine Translation by Jointly Learning to Align and Translate (https://arxiv.org/abs/1409.0473)
참조 : Visualizing A Neural Machine Translation Model (Mechanics of Seq2seq Models With Attention) (http://jalammar.github.io/visualizing-neural-machine-translation-mechanics-of-seq2seq-models-with-attention/)
참조 : 시퀀스 투 시퀀스 + 어텐션 모델 (https://www.youtube.com/watch?v=WsQLdu2JMgI&feature=youtu.be)
참조 : 모두를 위한 기계번역 (https://youtu.be/N4E53ZcUBJs)
참조 : KoreaUniv DSBA, Seq2Seq Learning (Kor) (https://youtu.be/0lgWzluKq1k)
참조 : Pytorch Seq2Seq Tutorial for Machine Translation (https://www.youtube.com/watch?v=EoGUlvhRYpk&feature=youtu.be)
참조 : Pytorch Seq2Seq with Attention for Machine Translation (https://youtu.be/sQUqQddQtB4)

이번 글에서는 attention 메커니즘에 대하여 살펴보도록 하겠습니다. attention이 자연어 처리 문제를

seq2seq 모델의 이해

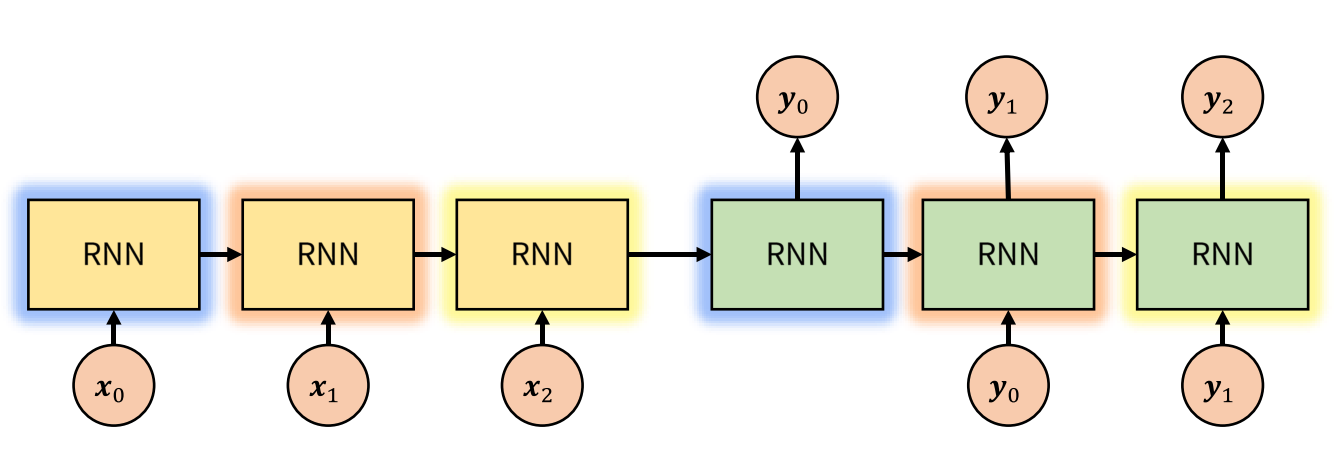
이번 글에서는 seq2seq(Sequence 2 Sequence)에 어떻게 Attention 모델이 사용되는 지를 통하여 Attention의 메커니즘에 대하여 다루어 보겠습니다.

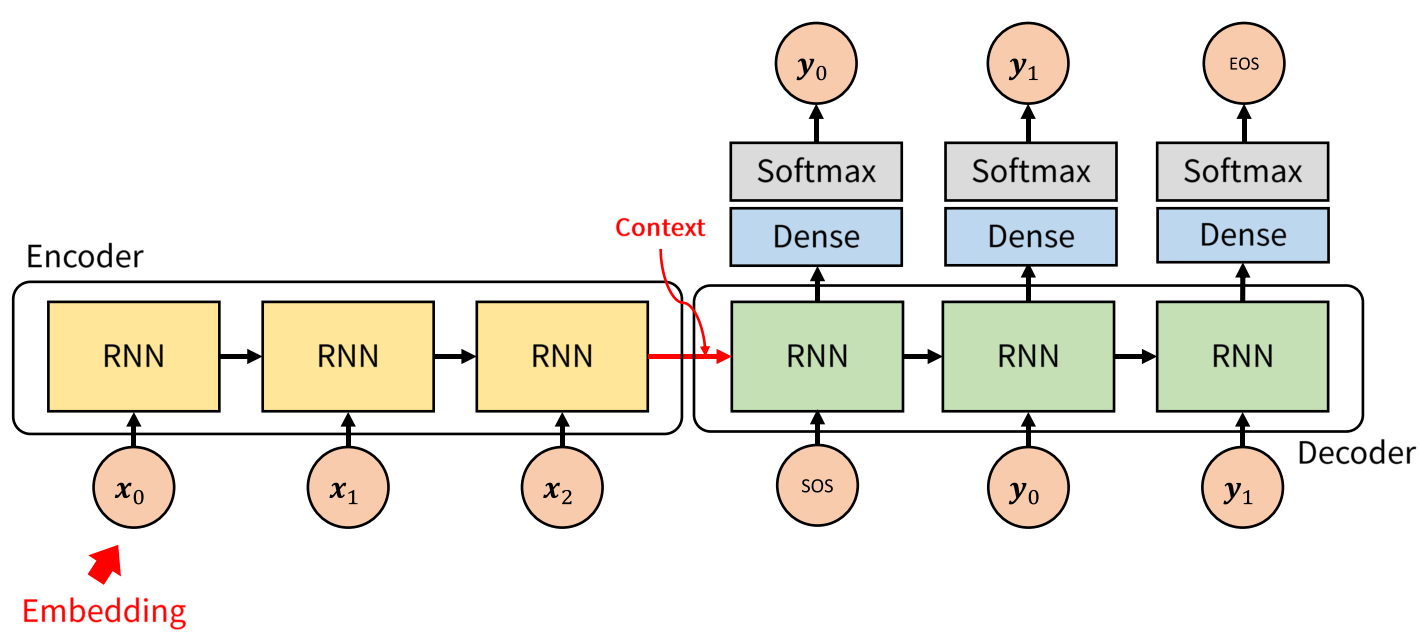
번역 문제를 다룰 때, 기본적으로 사용할 수 있는 seq2seq 모델은 위 그림과 같습니다. 먼저 입력으로 word2vec과 같은 Word Embedding방법을 통하여 얻은 embedding을 Encoder에서 입력으로 받습니다. 각 단어에 해당하는 embedding은 벡터 형태로 dense representation을 가집니다.
Encoder에서 각 단어의 embedding과 RNN의 hidden state를 거쳐서 정보가 압축이 되고 Encoder의 마지막 부분의 출력이 context vector가 됩니다. 즉, Encoder의 최종 목적은 context vector를 만드는 것에 있습니다. context vector는 간단하게 float로 이루어진 하나의 벡터입니다. 벡터의 크기는 모델을 처음 설정할 때 원하는 값으로 설정할 수 있으며 256, 512, 1024와 같은 숫자를 많이 사용하곤 합니다.
Decoder에서는 context를 입력으로 받습니다. 먼저 Decoder의 첫 부분은 context와 문장의 처음을 표시하는 SOS(Start of Sequence)를 입력으로 받습니다.
RNN을 거쳤을 때, hidden state는 계속 다음 step으로 연결됩니다. (Decoder의 RNN → RNN) 그리고 Dense - Sofmax를 거쳐서 \(y_{0}\)을 출력하였습니다. 그리고 \(y_{0}\)은 다시 RNN의 입력으로 들어가게 됩니다. 즉, Decoder의 RNN은 \(y_{i}\)와 hidden sate를 입력으로 받아서 \(y_{i+1}\)을 생성합니다.
지금 까지 설명한 내용이 seq2seq 모델의 가장 기본적인 형태입니다.
Jay Alammar의 비디오를 참조하면 다음과 같습니다.

하지만 Decoder에서 단순히 Encoder의 최종 출력인 context vector만 사용하는 것은 문제가 될 수 있습니다.
먼저 Gradient Vanishing 문제가 있을 수 있습니다. 왜냐하면 context vector를 기준으로 Encoder, Decoder가 완전히 분리되어 있으므로 입출력의 연관 관계가 너무 떨어져 있어서 backpropagation 시 gradient vanishing 문제로 학습이 잘 되지 않습니다.

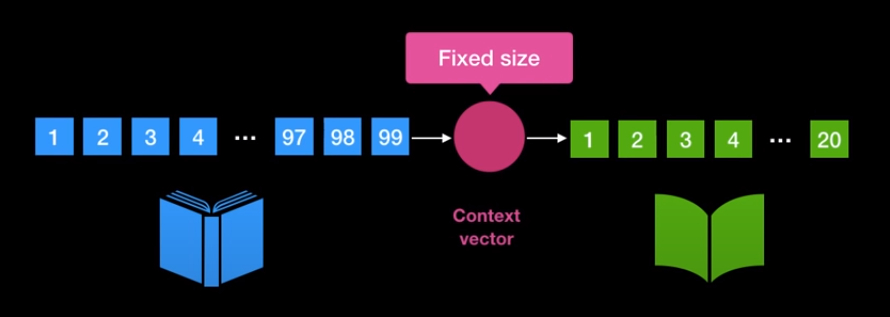
또한 각 단어에 해당하는 의미를 RNN을 거쳐서 하나의 벡터인 context vector안에 함축시키는 데 이 방법을 통하여 정보 손실이 발생할 수 있기 때문입니다. 위 그림과 같이 1개의 context vector 안에 99개의 단어 embedding vector의 정보를 모두 함축하는 것은 무리일 수 있습니다.
정보 손실을 막기 위하여 Encoder의 hidden state를 Decoder에서도 사용하는 방법을 생각할 수 있습니다.

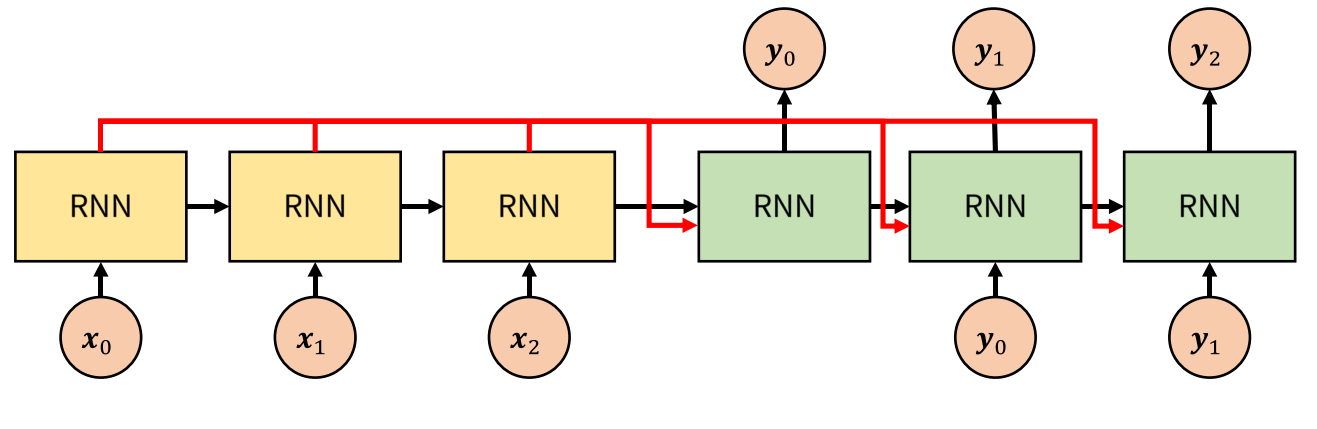
이와 같이 모델을 수정하면 크게 4가지 장점을 취할 수 있습니다.
① 여러 개의 단어 embedding을 1개의 context vector에 억지로 함축시킬 필요가 없어집니다.
② Decoder 입장에서 좀 더 다이나믹하게 Encoder의 hidden state를 활용할 수 있습니다. 예를 들어 Decoder에서 좀 더 집중하고 싶은 state에 좀 더 집중할 수 있도록 메커니즘을 설계할 수 있습니다.
③ RNN에서 입력된 지 오래된 데이터일수록 잊혀지는 문제가 있습니다. LSTM과 같은 모델에서 이 문제를 좀 더 개선하였지만 그럼에도 상대적으로 이전에 입력된 데이터에 대하여 출력에 영향이 낮아집니다. 하지만 위 그림과 같이 Encoder의 모든 hidden state를 사용하면 이 문제를 개선할 수 있습니다.
④ gradient highway가 생기기 때문에 gradient vanishing 문제에 좀 더 강건합니다.

하지만 이 경우에도 문제가 발생합니다. 먼저 Encoder의 입력에 따라서 Decoder에 얼마나 많은 입력이 들어가야 결정됩니다. 즉, 다양한 길이의 문장에 대하여 모델을 고정할 수 없습니다. 빨간색에 해당하는 크기가 문장의 길이에 따라서 변하게 되기 때문입니다.
또 다른 문제는 단순히 hidden state를 모두 넘겨주게 되면 입력의 차원이 굉장히 커지게 될 수 있습니다. 즉, sparsity 문제가 발생할 수 있습니다. 예를 들어 context만 Decoder의 입력으로 사용하는 경우 1개의 벡터만 Decoder의 입력이 되는 반면에 Encoder의 hidden state를 사용하는 경우 단어의 갯수 + context에 해당하는 벡터를 모두 입력으로 받게 되어 차원이 굉장히 커지게 됩니다. 데이터의 차원이 커지는 것은 성능에 악영향을 끼칠 수 있습니다.
이와 같은 문제를 해결하기 위하여 Attention 모델이 고안되었습니다.

Attention 메커니즘

먼저 Attention의 사전적 의미는 집중입니다. 이 의미는 Decoder에서 출력 할 때, 어떤 Encoder 정보에 집중해야 하는 지 알 수 있도록 하여 출력하는 데 도움을 주겠다는 뜻입니다. 이것이 Attention 메카니즘의 기본 아이디어 입니다.
Attention 메커니즘을 이해하기 위해서는 다음 용어에 대한 이해가 필요합니다.
Query : 질의. 찾고자 하는 대상
Key : 키. 저장된 데이터를 찾고자 할 때 참조하는 값
Value : 값. 저장되는 데이터
Dictionary : Key-Value가 쌍으로 이루어진 집합

{
    "Nation" : "South Korea",
    "City" : "Seoul" 
}

위 예제에서 Nation, City는 Key에 해당하고 South Korea, Seoul은 Valud에 해당합니다.

그러면 Querying 이라는 용어는 무엇인지 살펴보겠습니다.
위 그림과 같이 query(질의)에 해당하는 “2018”이 입력되었을 때, query에 해당하는 key 값을 찾아서 그 key 값에 해당하는 value를 출력하는 작업을 querying 이라고 합니다. 이 때, query와 똑같은 key값을 선택할 지 또는 가장 유사한 key값을 선택할 지는 문제에 따라 달라지게 됩니다.

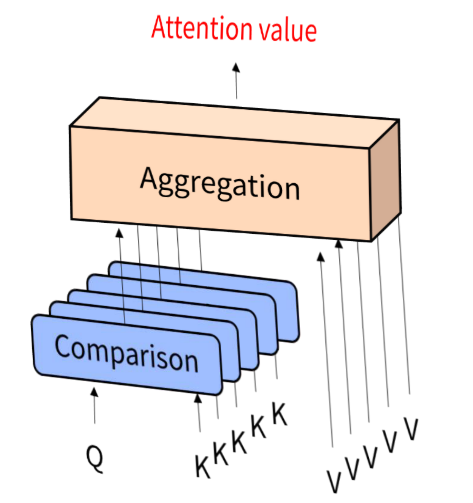
Attention에서는 Query에 대해서 어떤 Key와 유사한지 비교를 하고, 유사도를 반영하여 Key에 대응하는 Value를 합성(Aggregation)한 것이 Attention Value가 됩니다.
여기서 주목할 점은 Query는 하나이고 그 Query에 해당하는 Dictionary의 Key값들이 Query와 얼만큼 유사한지 계산을 한다는 점입니다.

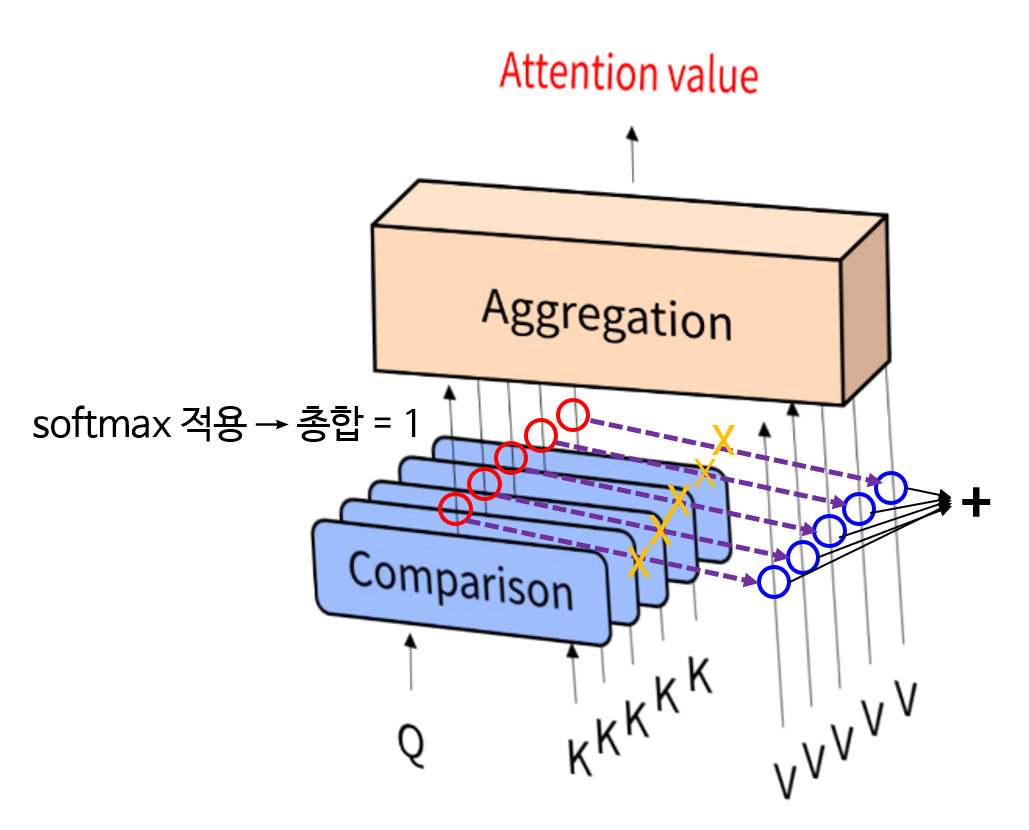
즉, 유사도에 해당하는 빨간색 원의 값과 value에 해당하는 파란색 원의 값을 곱한 후 모두 더한 것이 Attention value가 됩니다. 마치 유사도가 가중치 처럼 곱해지게 됩니다. 이 때, 연산은 벡터의 내적과 벡터의 합을 통한 연산이 됩니다.
그렇다면 Query는 무엇이 될까요? Query는 Decoder의 hidden state가 됩니다. Decoder의 RNN에 입력되는 하나 앞선 time-step의 hidden state 입니다.
그렇다면 Attention에서 사용하는 Key와 Value는 무엇일까요? Attention에서는 Encoder의 hidden state를 Key와 Value로 사용합니다. 즉, Key와 Value는 같고 단어의 갯수 만큼 Key 값을 가집니다. 참고로 대부분의 attention network에서는 key와 value를 같은 값을 가지도록 합니다.

여기서 Comparison과 Aggregate는 구현 방식에 따라 다를 수 있으나 오리지널 아이디어의 경우 Compare는 Fully Connected 방식의 연산을 이용하였고 Aggregate의 경우 모든 key-value에 대하여 벡터의 element-wise multiplication 연산을 한 후 element-wise sum을 하여 Attention Value를 생성합니다. 수식은 아래와 같습니다.

\[\text{Compare}(q, k_{j}) = q \cdot k_{j} = q^{T}k_{j}\]
\[\text{Aggregate}(c, V) = \sum_{j} c_{j}v_{j}\]

그러면 Attention 모델을 seq2seq에 적용해 보도록 하겠습니다.

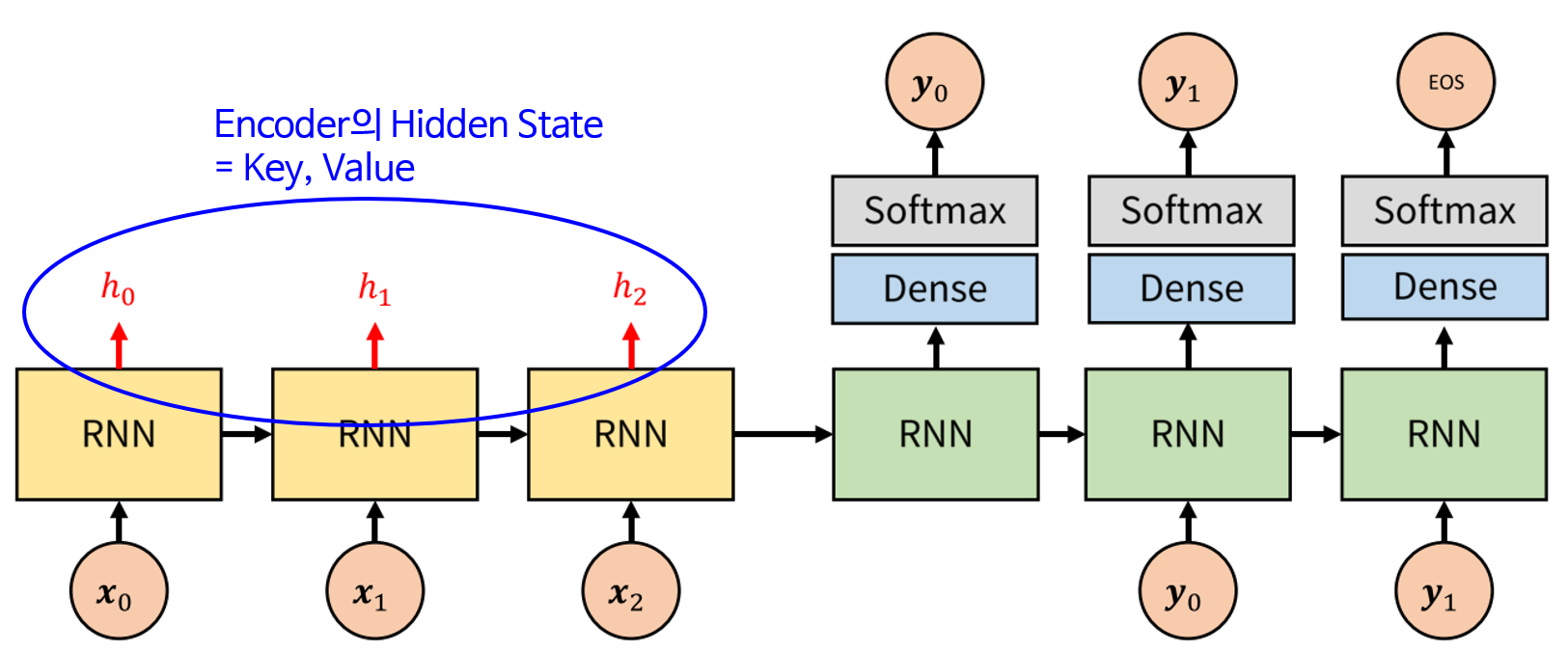
앞에서 설명하였듯이 Encoder의 hidden state는 (Key, Value)로 사용됩니다. 따라서 위 그림에서 \(h_{i}\)는 Key와 Value로 사용됩니다.

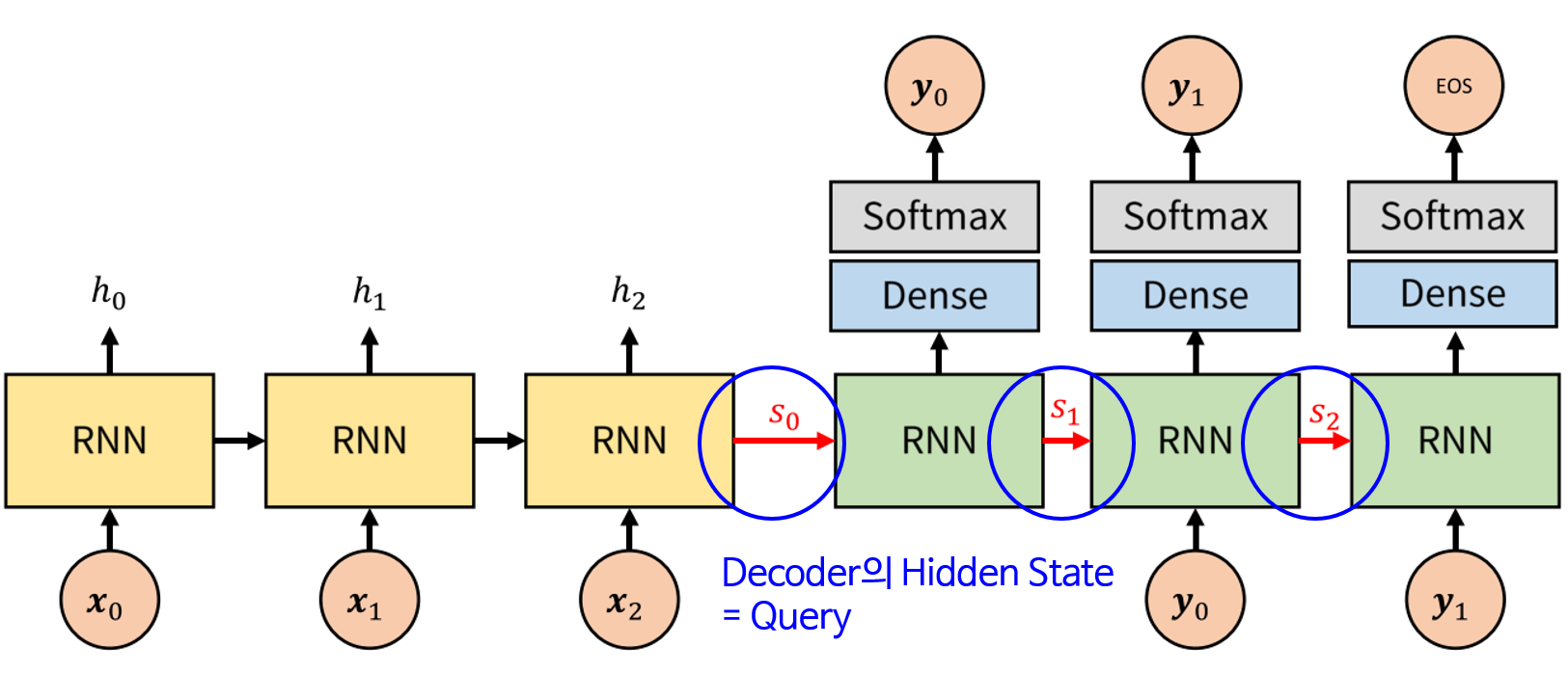
Decoder의 hidden state는 Query로 사용됩니다. 따라서 위 그림에서 \(s_{i}\)는 Query로 사용됩니다.

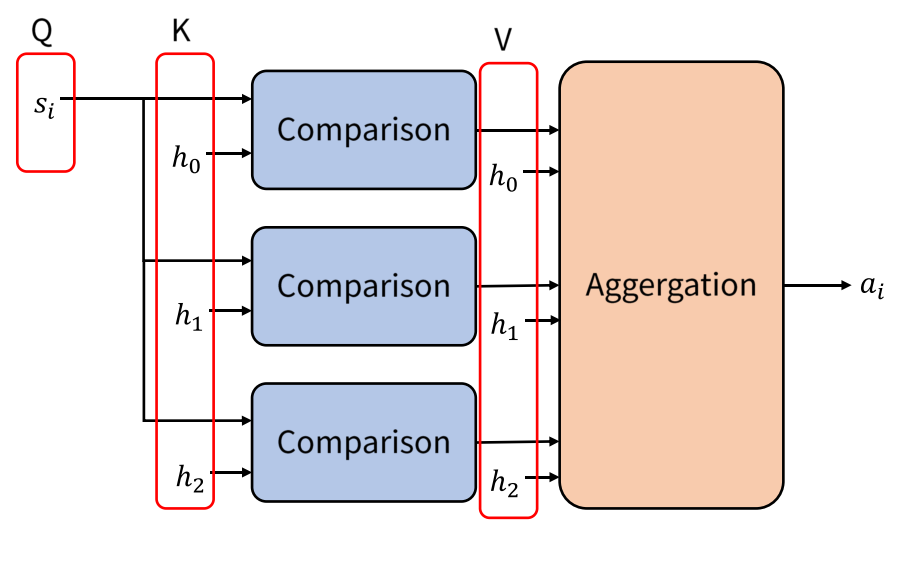
Attention 관련 연산은 위 메커니즘을 따릅니다. Decoder에서 \(s_{i}\)라는 Query가 입력되고 그 Query와 모든 key 값인 \(h_{i}\) (위 그림에서는 \(h_{0}, h_{1}, h_{2}\))와 Comparison 이라는 연산을 통하여 유사도를 구합니다. 이 유사도 값은 softmax를 거치기 때문에 확률 값처럼 총 합이 1이 됩니다.
그러면 Value에 해당하는 \(h_{i}\)와 유사도를 곱하고 (element-wise multiplication) 그 결과들을 합하여 최종적으로 \(a_{i}\) 라는 Attenen value를 출력합니다.
위 그림에서 사용된 연산을 수식으로 표현하면 다음과 같습니다.

\[c_{i} = \text{softmax}(s_{i}^{T}h_{j})\]
\[a_{i} = \sum_{j}c_{i}h_{j}\]

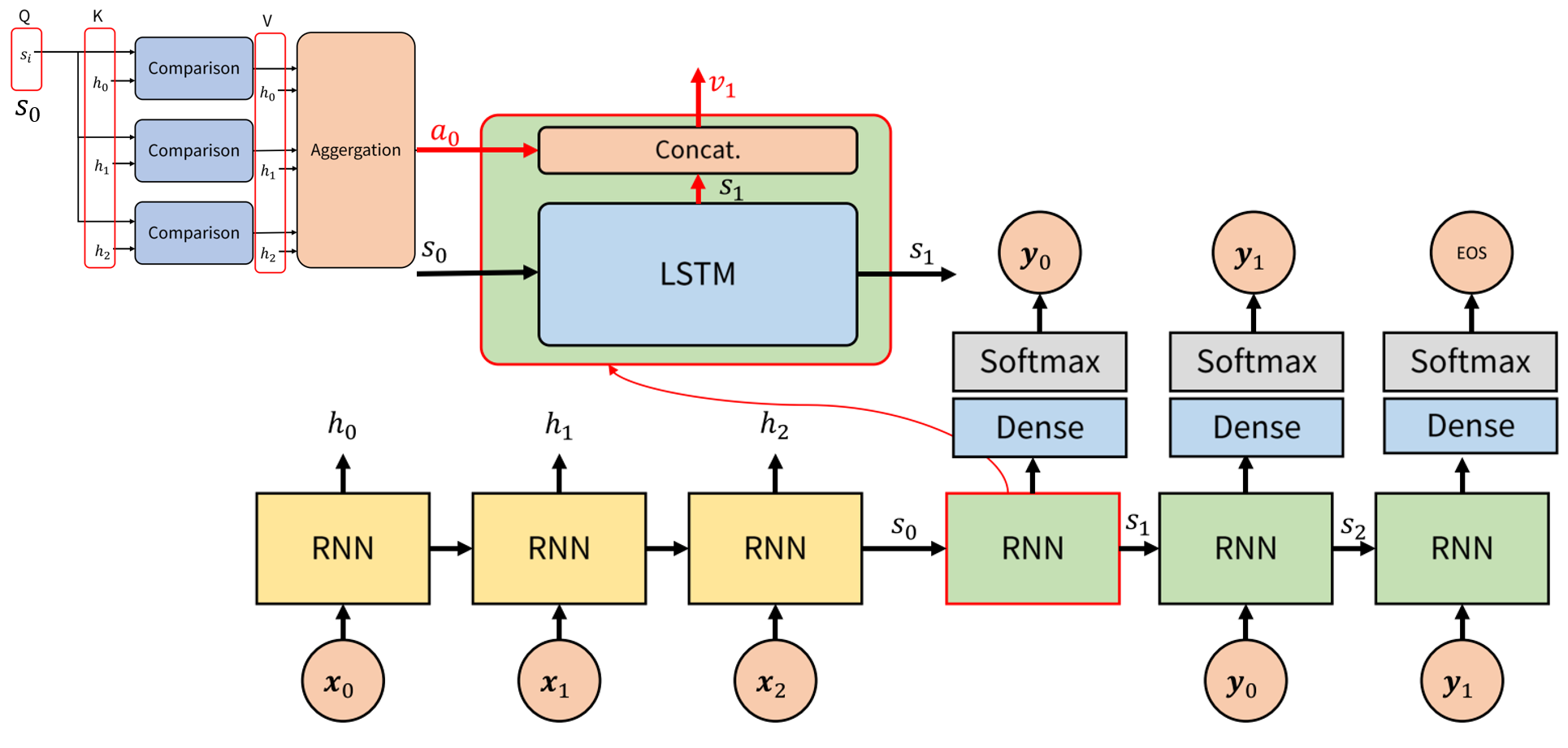
먼저 Decoder의 hidden state는 RNN(LSTM)에서 받아서 연산하여 \(s_{i}\) → \(s_{i+1}\)로 만듭니다.
그 후 Attenen value인 \(a_{i}\)와 \(s_{i+1}\)을 concat (\(v_{i} = [s_{i}; a_{i-1}]\)) 하여 \(v_{i+1}\)을 만듭니다. 이 값을 FC layer와 Softmax를 거쳐서 최종 출력인 \(y_{i}\)를 출력합니다.

영상 데이터 관점에서의 Attention

이미지 처리를 위한 딥러닝에서 일반적으로 많이 사용하는 방식은 Convolution 연산을 사용하는 방식입니다.

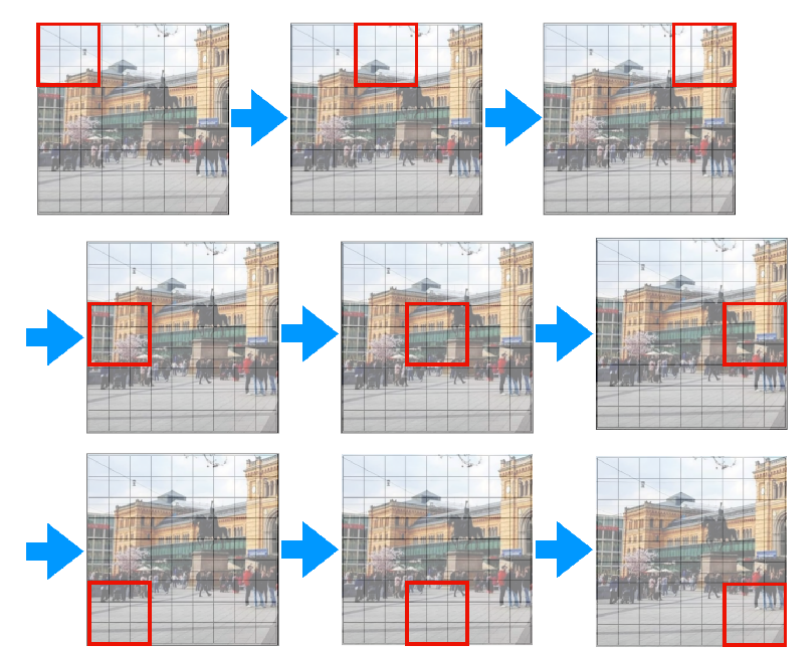
Convolution 연산을 사용하면 위 그림과 같이 빨간색 영역의 필터를 순차적으로 이동하면서 각 영역의 정보를 읽어들입니다.
이와 같이 각 필터가 local한 영역의 정보를 읽어서 이해하고 layer가 쌓이면서 점점 더 넓은 영역의 정보를 읽어들이는 것이 convolution layer의 동작 방식입니다.
이 특성이 convolution layer의 장점이자 단점이 되는데 얕은 layer에서는 local 영역을 자세하게 볼 수 있고 깊은 layer에서는 점점 더 넓은 영역을 볼 수 있어서 자세하면서 넓게 볼수 있는 장점을 가지는 반면 다음과 같은 두 영역을 한번에 고려하지는 못합니다.

일반적인 convolution 연산을 사용하는 뉴럴 네트워크에서는 한번에 위 2가지 영역을 고려하지는 않습니다. 앞에서 설명한 바와 같이 점점 더 receptive field를 넓혀가는 구조이지 convolution 필터가 왼쪽 상단을 볼 때, 동시에 전체를 고려하지 않습니다. 이러한 점이 convolution 연산의 단점이 될 수 있습니다.

예를 들어 위 그림과 같이 고양이를 인식할 떄, convolution 연산은 두 귀를 한번에 보고 인식할 수는 없습니다. layer가 깊어져서 한번에 고양이 전체를 볼 수는 있어도 지엽적으로 두 부분만을 볼 수는 없는 것이 convolution 연산의 아쉬운 부분입니다.

attention 개념은 주어진 어떤 입력에 대하여 어떤 부분을 중심적으로 볼 지 가중치를 주는 것으로 이해할 수 있습니다. 기본적으로 Attention이란 개념을 설명할 때 Query, Key, Value 개념을 이용하여 설명을 하는데 이 개념이 필수적인 것은 아니며 어떤 부분을 중심적으로 볼 지에 대한 컨셉이 있으면 attention으로 생각할 수 있습니다.

예를 들어 아래와 같은 개념 또한 attention의 일종으로 볼 수 있습니다.

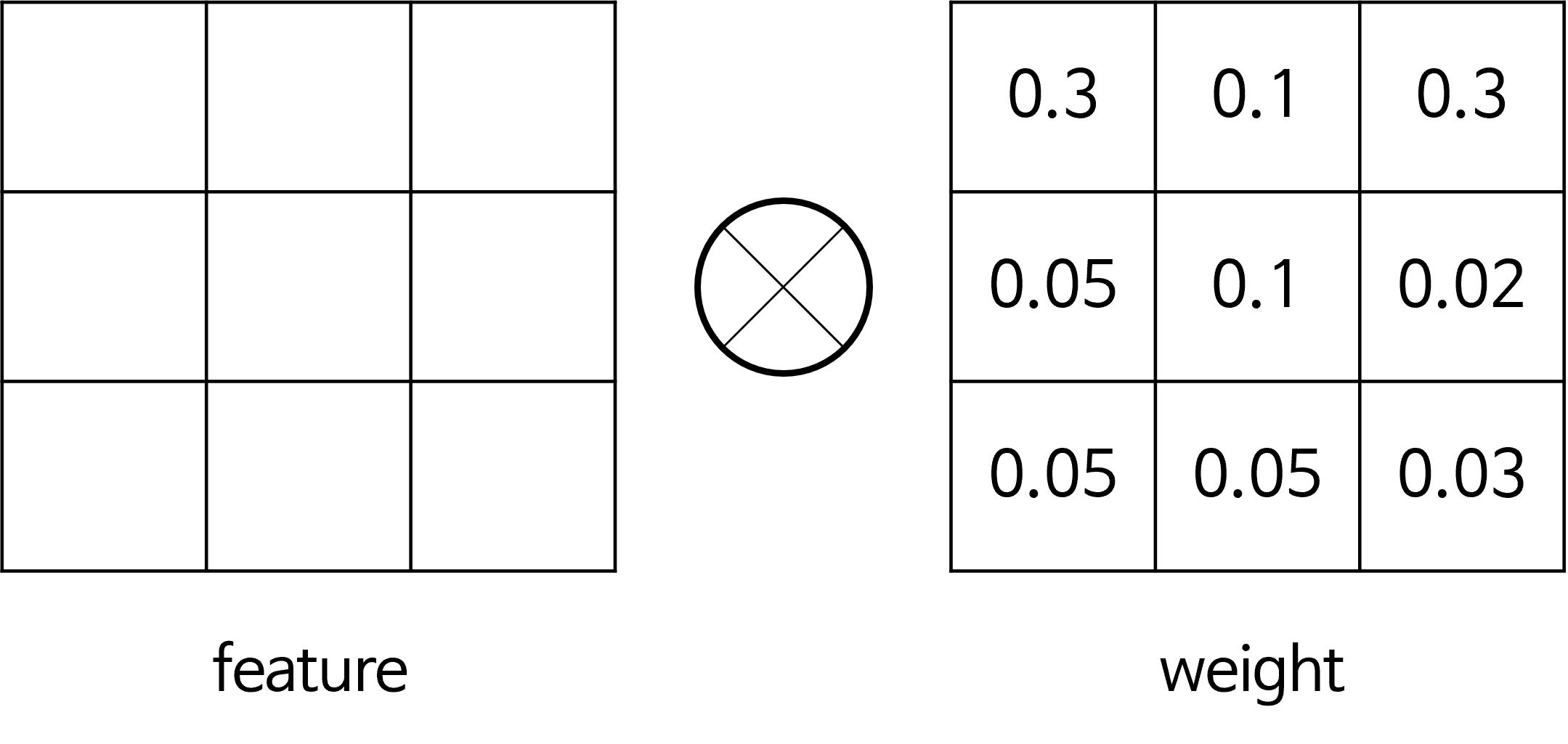
왼쪽과 같이 convolution layer를 거친 feature가 있고 이 feature와 연산이 되는 mask가 있다고 하였을 때, mask와 곱해진다면 어떤 부분은 큰 값이 곱해져 크게 활성화가 되고 어떤 부분은 값이 작아지게 됩니다.
즉, 어떤 부분을 집중해서 봐야 할지 정해지게 되므로 attention의 역할을 할 수 있게 됩니다. 이와 같은 방식 또한 간단한 attention의 메커니즘으로 볼 수 있습니다.

BAM : Bottleneck Attention Module

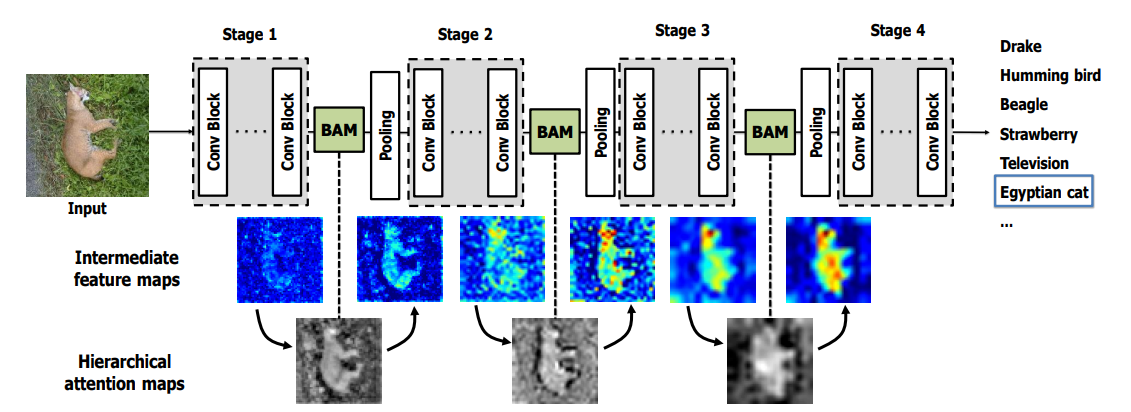
위 그림은 BAM (Bottleneck Attention Module)이라는 논문에서 제안한 구조의 attention 메커니즘 입니다.
위 그림과 같이 BAM을 거치면 layer 초반부터 background와 같은 부분에 대한 집중을 줄이게 됩니다. 즉, low-level feature에 대한 영향을 줄이게 되는 것입니다. 반면에 high-level feature인 실제 객체에 집중하게 만들어 줍니다.
BAM의 수식을 살펴보면 아래와 같습니다.

\[F' = F + F \bigotimes M(F)\]
\[\text{feature map} F \in \mathbb{R}^{C \times H \times W}\]
\[\text{attention map} M(F) \in \mathbb{R}^{C \times H \times W}\]

위 식에서 \(\bigotimes\) 는 element-wise multiplcation 을 의미합니다.
이와 같이 layer를 거치면서 BAM이 집중하고자 하는 영역을 선택하는 것이 attention의 역할을 하는 것과 동일합니다. 좀더 자세히 살펴보면 아래와 같습니다.

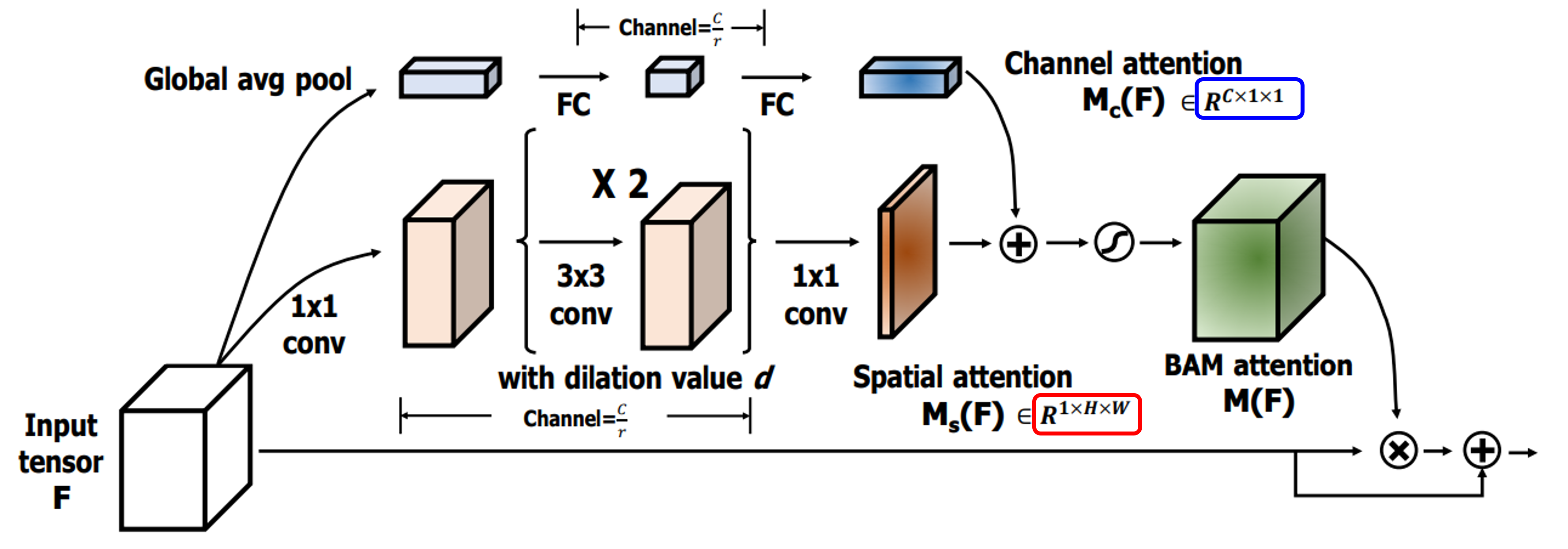
위 그림과 같이 \(M(F)\) 는 아래 식과 같이 나타낼 수 있습니다.

\[M(F) = \sigma(M_{c}(F) + M_{s}(F))\]
\[M_{c}(F) \in R^{c}\]
\[M_{s}(F) \in R^{H \times W}\]

위 그림과 같이 \(M()\) 은 2개의 요소인 \(M_{c}()\) 와 \(M_{F}()\) 를 각각 추출한 다음에 \(\bigoplus\) 즉, 채널 방향으로 broadcasting 연산을 통해 최종 attention map을 생성합니다. 각 요소의 구성 방법은 위 그림과 같으며 수식으로 나타내면 아래와 같습니다.

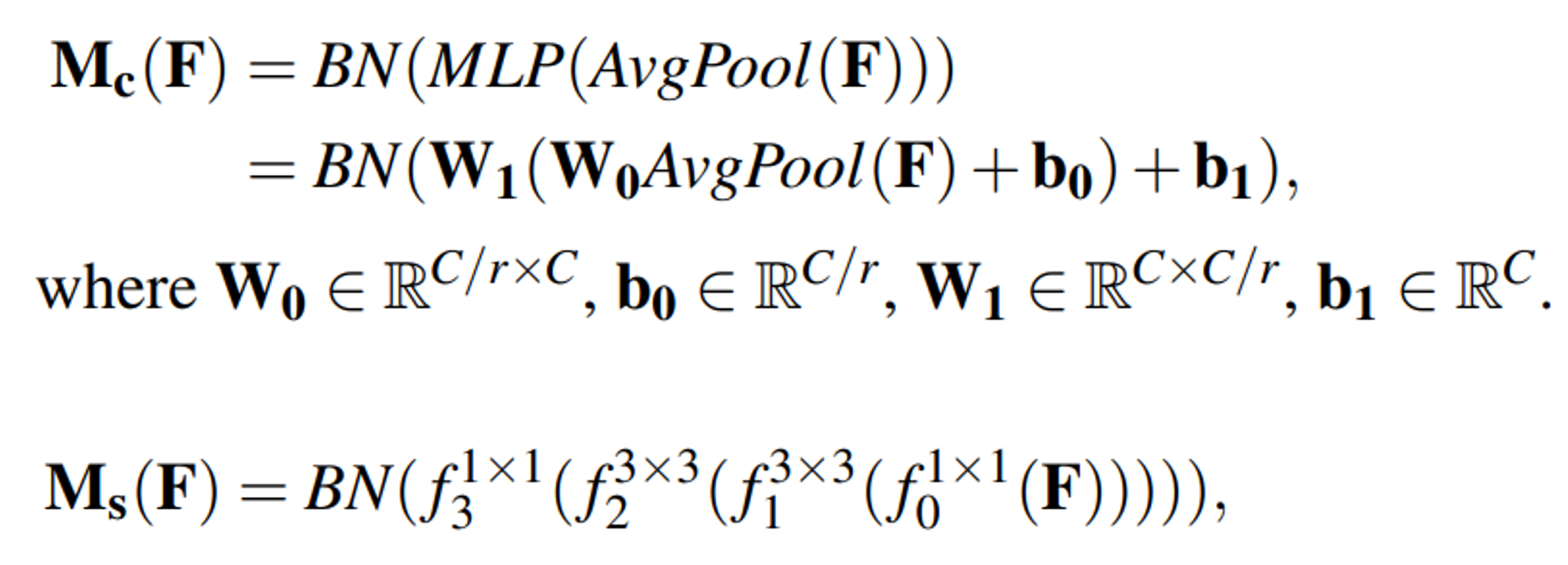
이렇게 만들어진 BAM을 이용하여 \(F' = F + F \bigotimes M(F)\) 연산을 하면 feature 중 high-level feature에 attention을 적용할 수 있다고 논문에서는 설명합니다.

지금까지 살펴본 방법은 흔히 알려진 Key, Query, Value 를 이용한 방법이 아닌 다른 방식의 attention 방법 중 하나입니다. 본 글에서 이와 같은 방식을 언급한 이유는 Key, Query, Value 방식의 attention은 수단이지 목적이 아님을 명시하기 위함입니다.
그러면 흔히 알려진 Key, Query, Value 방식의 attention 메커니즘을 컴퓨터 비전 사례를 통해 살펴보겠습니다.

Key, Query, Value 기반의 Attention 메커니즘

deep learning 관련 글 목차