AutoEncoder의 모든것 (1. Revisit Deep Neural Network)

이 글은 오토인코더의 모든것 강의를 보고 요약한 글입니다.

AutoEncoder와 관련된 키워드는 다음과 같습니다.
- Unsupervised Learning
- Representation learning = Efficient coding learning
- Dimensionality reduction
- Generative model learning
여기서 가장 많이 알려진 키워드가 Dimensionality reduction 이고 많은 사람들이 이 용도로 AutoEncoder를 사용하고 있습니다.
Dimensionality reduction을 하기 위해서는 AutoEncoder가 feature를 잘 추출해야 하는데 이 의미가 Representation learning과 연관되어 있습니다.

Nonlinear Dimensionality Reduction과 같은 용도로 사용되는 키워드는 위와 같습니다. 앞에서 언급한 Feature Extraction과 Manifold learning은 같은 의미로 많이 사용되는 용어입니다.

이번 글에서 살펴볼 AutoEncoder은 어떤 목적의 알고리즘으로 분류되는 지 먼저 살펴보겠습니다.

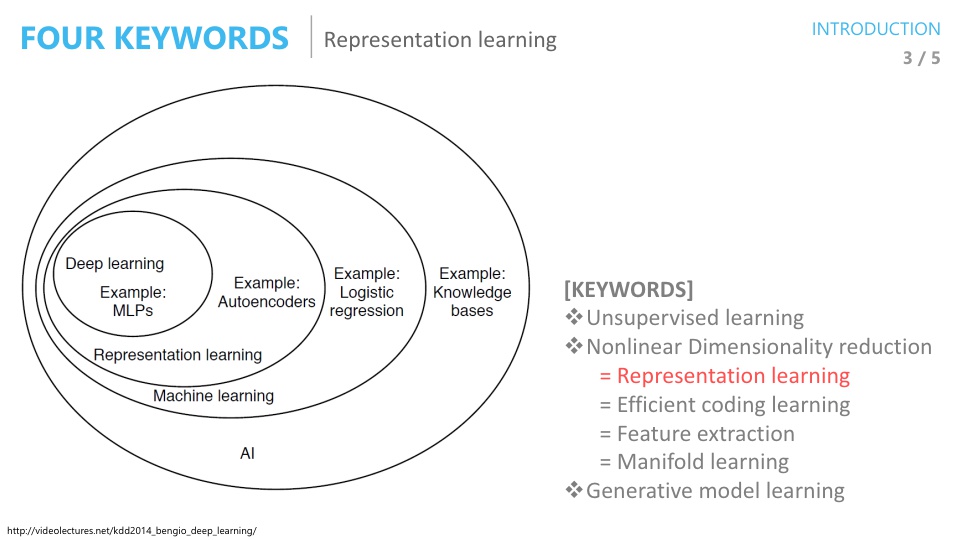
위 표는 벤지오 교수님의 기술분류표이고 AutoEncoder는 Representation Learning으로 분류되어 있습니다.

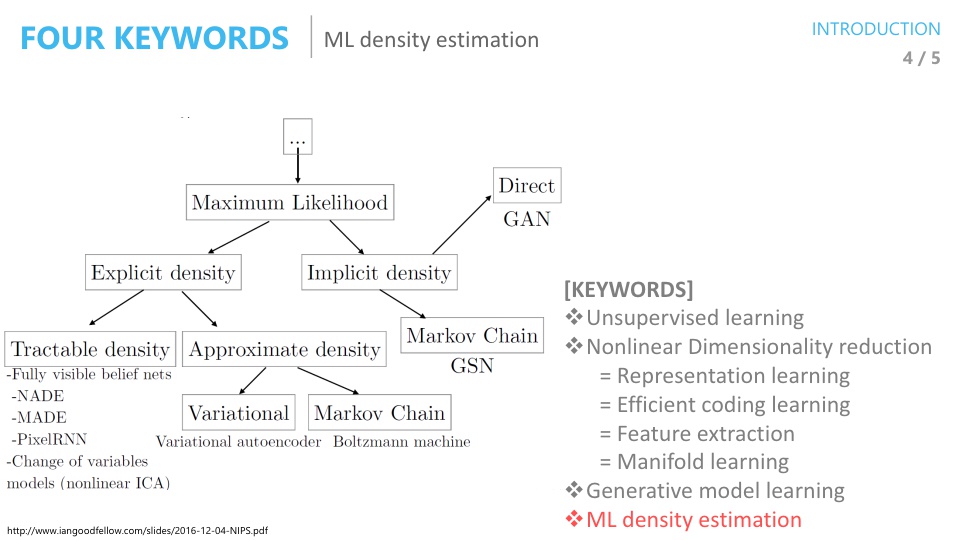
이안 굿펠로우의 기술분류표를 보면 앞으로 살펴 볼 Variational Autoencoder는 Maximum Likelihood와 연관이 되어 있습니다.
따라서 Maximum Likelihood에 대해서도 알아 볼 예정입니다.

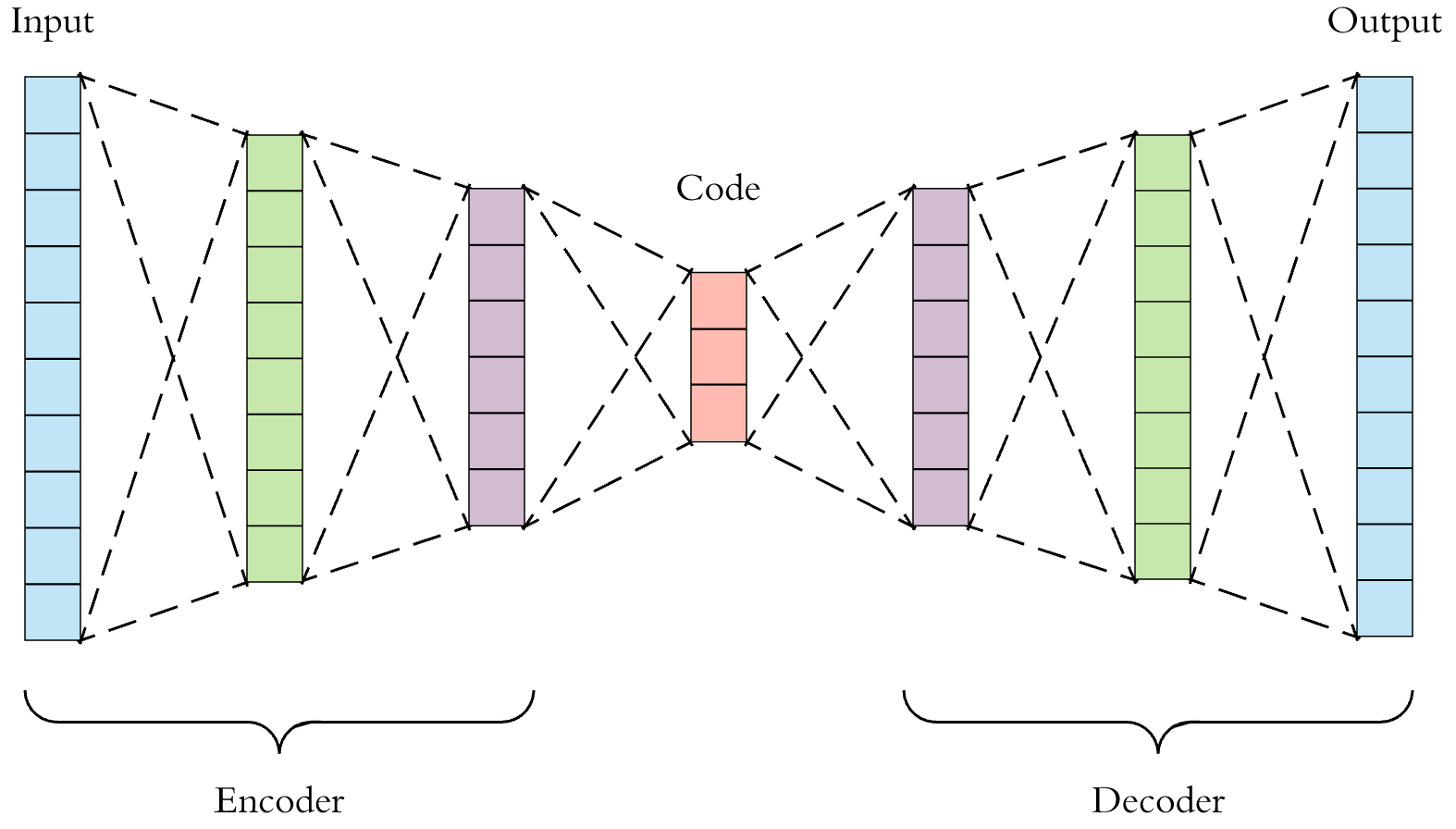
AE(AutoEncoder)는 입력과 출력이 같은 동일한 구조를 가지고 있으며 그러한 이유로 Auto Encoder라고 불립니다.
이 때 관계된 키워드가 앞에서 언급한 바와 같이 크게 4가지가 있습니다.
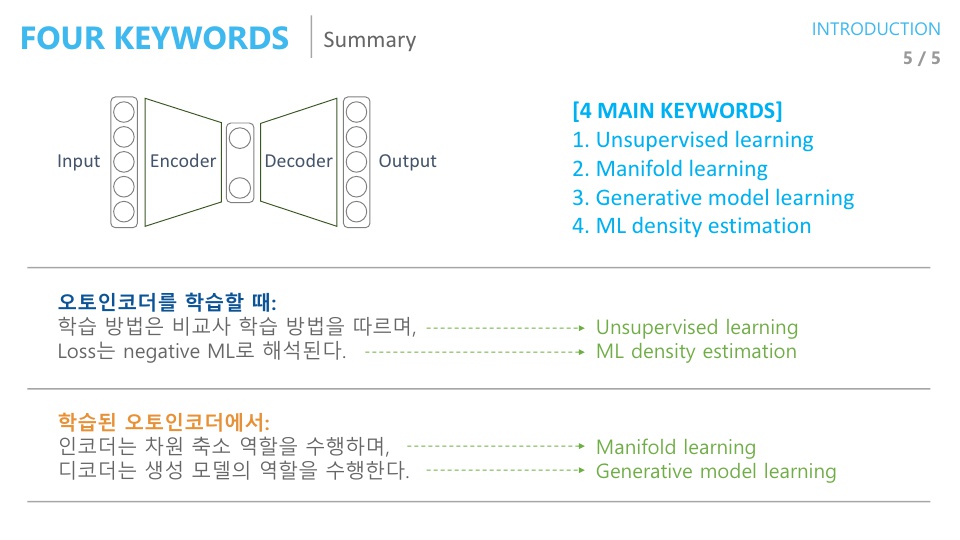
오토인코더를 학습할 때,
- Unsupervised learning : 학습 방식에 해당합니다.
- ML density estimation : Loss function이 Negative Maximum Likelihood로 해석을 해서 Loss를 Minimize 하면 Maximum Likelihood가 됩니다.
학습된 오토인코더에서
- Manifold learning : 인코더는 차원 축소 역할을 수행하고 (일반적으로 가운데 차원은 입력 보다 작음) 이것을 Manifold learning 이라고 합니다.
- Generative model learning : manifold learning을 한 결과를 다시 입력 차원과 똑같이 복원을 하는 데 이것을 Generative model 이라고 합니다.

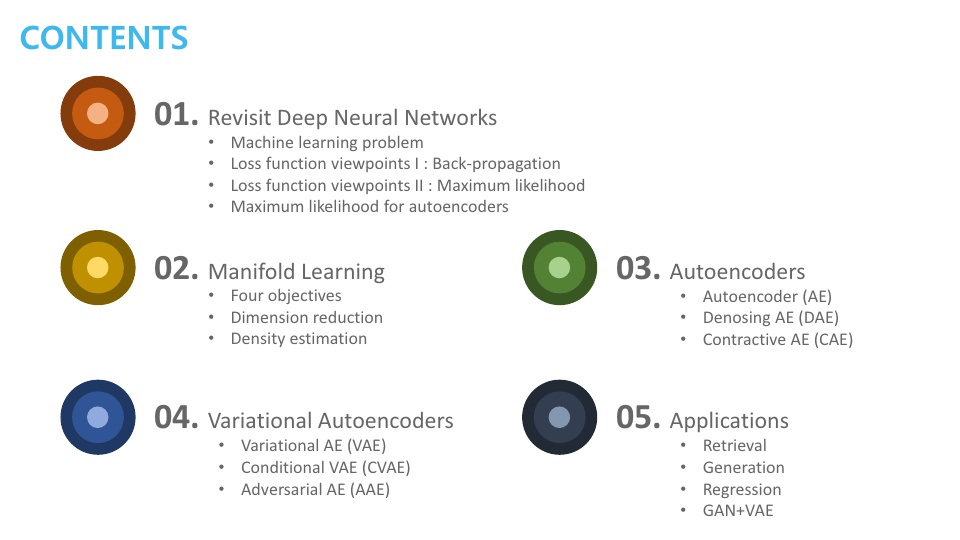
앞으로 다룰 내용은 위의 슬라이드에 있는 구성으로 진행할 것입니다.
챕터 1, 2는 Variational AutoEncoder(VAE)를 이해하기 위한 사전지식으로 구성되어 있습니다.
- 챕터1은 AE가 Maximum Likelihood(ML)과 관련이 있음을 설명합니다.
- 챕터2는 AE가 Manifold learning에 많이 쓰이기 때문에 Manifold learning에 대한 정의에 대하여 알아보도록 하겠습니다.
챕터 3에서는 기본적인 AE에 대하여 다루어 보도록 하겠습니다.
챕터 4에서는 VAE에 대하여 다루어 보도록 하겠습니다.
챕터 5에서는 AE를 응용하는 방법에 대하여 알아보도록 하겠습니다.

챕터1을 시작해 보겠습니다. 챕터1에서는 AE는 Maximum Likelihood하는 작업인 것을 이해하면 되겠습니다.

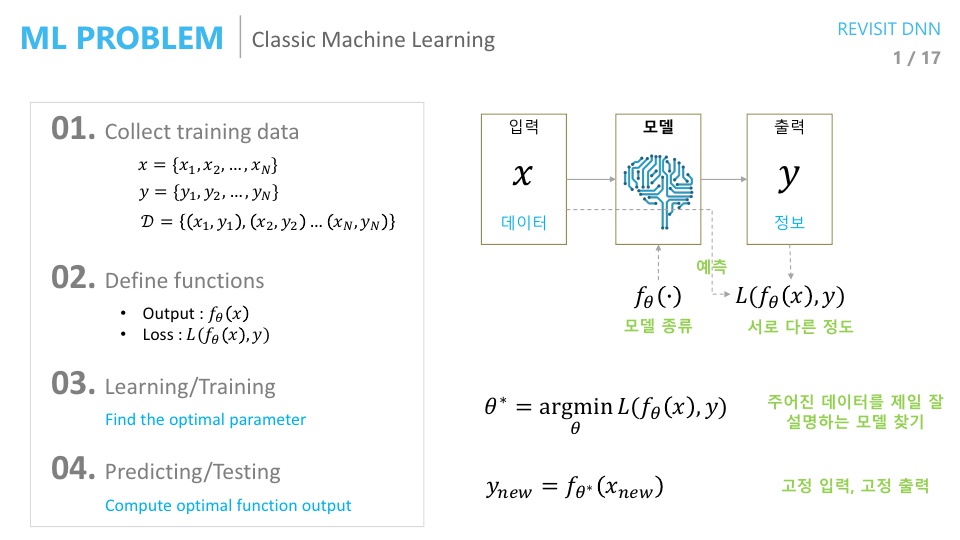
먼저 전통적인 머신러닝 방법부터 살펴보도록 하겠습니다.
머신러닝을 할 때에는 주어진 데이터가 있으면 그 데이터에서 필요한 정보를 뽑아내야 합니다. (얼굴이 있으면 이것은 얼굴이다? 또는 누구의 얼굴이다와 같은 추상적인 정보)
① 따라서 먼저 학습을 하기 위한 데이터를 먼저 모아야 합니다. 특히 위의 슬라이드를 보면 \(x, y\) 데이터를 모아서 데이터 셋 \(D\)를 구성하게 됩니다. 이 데이터 구성은 supervised learning을 위한 방법입니다.
② 입력 데이터를 마련하였다면 그 다음은 학습할 모델을 준비해야 합니다. 즉, 주어진 데이터에서 추상적인 답을 뽑아낼 알고리즘을 정의해야 합니다.
③ 모델을 정의한 다음에는 모델을 결정지을 파라미터를 학습하여 결정해야 합니다. 이 때 학습을 하기 위해 Loss function을 정의해야 합니다. 정의한 Loss function을 이용하여 모든 데이터셋에 걸쳐서 예측값과 정답간의 차이를 가장 좁혀주는 파라미터를 찾습니다.
④ 학습이 완료되면 예측을 하고 성능을 테스트 합니다.

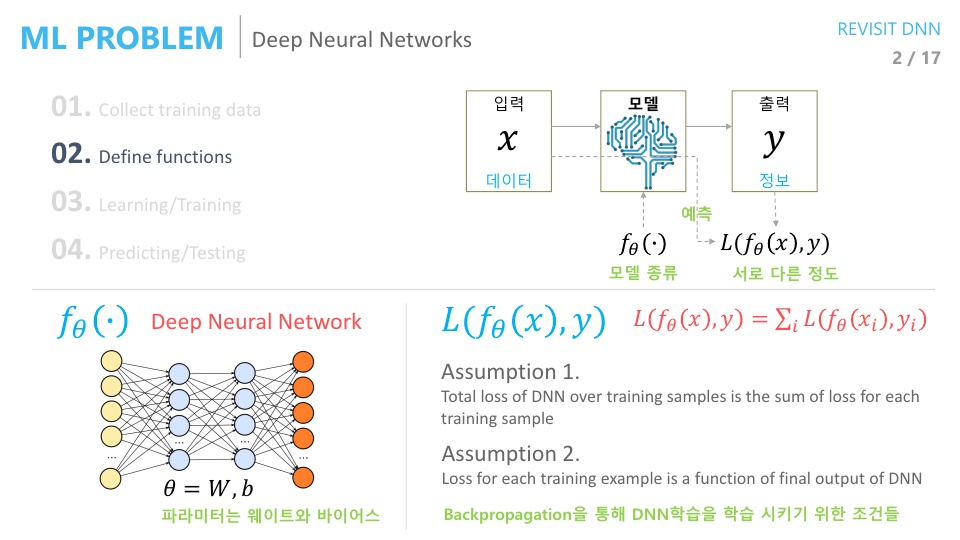
딥러닝에서는 위에서 설명한 머신러닝 방법에서 모델 설정 방법이 조금 바뀌게 됩니다.
딥러닝에서는 모델을 Deep Neural Network를 사용하는것으로 정의합니다.
그리고 딥러닝에서는 Loss function을 정의할 때 주로, Mean Squared Error, Cross Entropy등을 사용합니다. 왜냐하면 Back-propagation을 하기 위해서 입니다.
Back-propagation을 통해서 딥 뉴럴 네트워크를 학습해야 하고 위에서 언급한 2가지 Loss가 효율적으로 사용될 수 있습니다.
딥러닝에서는 뉴럴네트워크 구조로 인하여 Back-propagation을 통한 학습을 해야 하는데, 이 때 필요한 2가지 조건이 있습니다. 이 조건을 만족하는 Loss가 MSE와 CE입니다.
- 조건 1 : 전체 데이터셋에 대한 Loss는 각각의 데이터의 Loss의 합과 같다.
- 조건 2 : Loss를 구성할 때, 네트워크의 출력값 만을 사용한다.

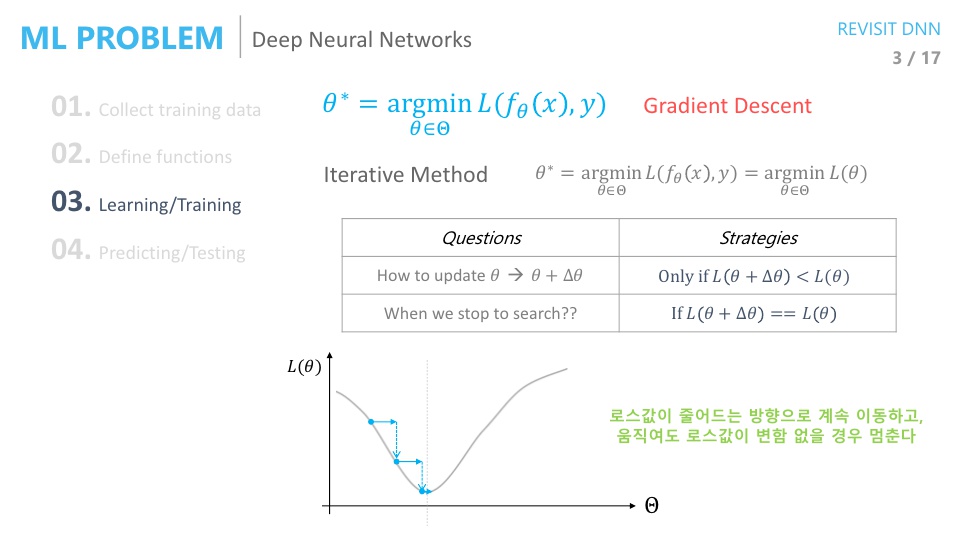
전체 학습 데이터 셋에 대한 Loss를 최소화 하는 파라미터를 찾는데 주로 사용하는 방법은 Gradient Descent입니다.
Gradient Descent(GD)는 기본적으로 iterative 한 방식입니다. Closed form이 아니므로 한번에 솔루션을 찾지는 못하고 여러번 시도 끝에 솔루션을 찾아가는 구조입니다.
Iterative method에는 2가지가 결정되어야 합니다.
- ① 어떻게 파라미터를 업데이트 할 것인가 ? GD에서는 Loss값이 줄어들기만 하면 업데이트를 하는 전략을 취합니다.
- ② 언제 업데이트를 멈출 것인가? GD에서는 파라미터를 아무리 바꾸더라도 Loss가 줄어들지 않으면 업데이트를 멈춘다는 전략을 취합니다.

그런데 한가지 문제점이 있습니다. 업데이트 해야 할 파라미터 \(\theta\)의 차원이 굉장히 큰 경우에는 어떻게 \(\theta\)를 변경해야 할까요?
즉, 어떤 방법으로 파라미터를 업데이트 해야 할 지에 대한 전략이 필요합니다.
앞의 전략(Loss가 줄어드는 방향으로 파라미터 업데이트)을 만족시키면서 파라미터를 변경하는 방법에 대하여 알아보겠습니다.
머신러닝, 딥러닝에서 사용하는 파라미터 업데이트 방법의 기본은 taylor expansion에 기초를 두고 있습니다.

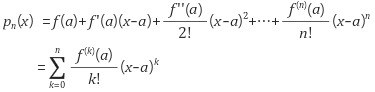
taylor expasion의 정의는 위와 같습니다.
간단히 말하면 변경 전 정의역의 치역값 \(f(a)\) 에 정의역의 변경값과 1차 미분값의 곱 \(f'(a)(x-a)\) , 정의역의 변경값과 2차미분값의 곱 \(f''(a)/2! (x-a)^{2}\) , … 을 모두 더하면 변경 후 정의역의 치역값 \(p_{n}(x)\) 이 된다는 것입니다.
머신러닝에서는 이 taylor expansion의 방법에서 1차 미분값까지만 사용해서 근사값을 추정하는 방식을 사용합니다.
즉, \(\theta\) 를 바꾸었을 때의 Loss 값은 현재 Loss 값 + 그래디언트 * \(\theta\)의 변경량이 됩니다.
taylor expansion에서는 어떤 값( \(x=a\) )을 기준으로 미분하였으므로 \(x=a\)에서 다항근사를 하는 것이지만 그 주변까지도 어느 정도는 근사가 됩니다.
이 근사가 되는 범위는 몇 차수 미분 까지 사용하는 것과 관계가 있습니다. 더 많은 차수를 사용할수록 더 넓은 지역을 작은 오차로 표현이 가능합니다.
예를 들면 sin 함수에서 기울기가 1인 부분이 있습니다. 그 지점에서만 국소적으로 바라봤을 때는 sin(x) 함수와 y=x 함수가 똑같아 보입니다. 하지만 그 지점을 조금 더 벗어나면 sin(x)와 y=x값이 달라보이게 됩니다.
만약 근사값을 사용할 때, 1차 미분이 아니라 2차, 3차, … 미분까지 사용한다면 y=x 함수식 보다 조금 더 복잡하지만 그 부근에서 y=x 일 때 보다 좀 더 넓은 범위로 sin(x)와 똑같아 보이는 근사식을 구할 수 있습니다.
그러면 1차 미분값 까지만 사용한 근사식을 이용하여 Loss값의 변화량을 살펴보면 위 슬라이드와 같이 \(\triangle L \approx \nabla L * \triangle \theta\)가 됩니다. 참고로 \(\triangle\) 은 변화량(델타)을 뜻하고 \(\nabla\)는 그래디언트(미분값)을 뜻합니다.
만약 \(\triangle \theta = -\eta\nabla L\) 라고 한다면, \(\triangle L = -\eta \Vert \nabla L \Vert < 0\) 이 됩니다.
- 이 때, \(\eta\)가 양수이고 흔히 아는 learning rate를 뜻합니다.
- 위 식에 의해서 \(\triangle L\)은 항상 음수가 되로 Loss는 줄어드는 방향으로 업데이트가 됩니다.
그러면 \(\triangle \theta = -\eta\nabla L\) 라는 가정은 왜 두었을까요? 앞에서 설명한것과 같이 Loss 값을 항상 줄이는 방향으로 만들어 학습이 되도록 만들기 위해서입니다.
즉 \(\triangle \theta = -\nabla L\)이 되도록 하면 항상 Loss는 줄어들게 되고 여기에 \(\eta\) 값을 곱해주어서 학습이 잘 될수 있도록 \(\triangle \theta\) 값의 변경량을 조절해 줍니다.
이 때 Learning rate \(\eta\)를 작은 값을 사용하는 이유는 파라미터 값을 조금씩 바꾸기 위함입니다.
파라미터 값을 조금씩 바꿔야 하는 이유는 Loss 함수에서 taylor expasion의 1차 미분항까지만 사용했기 때문에 아주 좁은 영역에서만 감소 방향이 정확하기 때문입니다. 즉, 파라미터 변경량이 크면 근사를 잘못할 수 있기 때문에 learning rate를 이용하여 변경량을 적당히 줄여줍니다. learning rate가 너무 커서 Loss가 발산하는 경우가 바로 approximation을 잘못한 경우입니다.

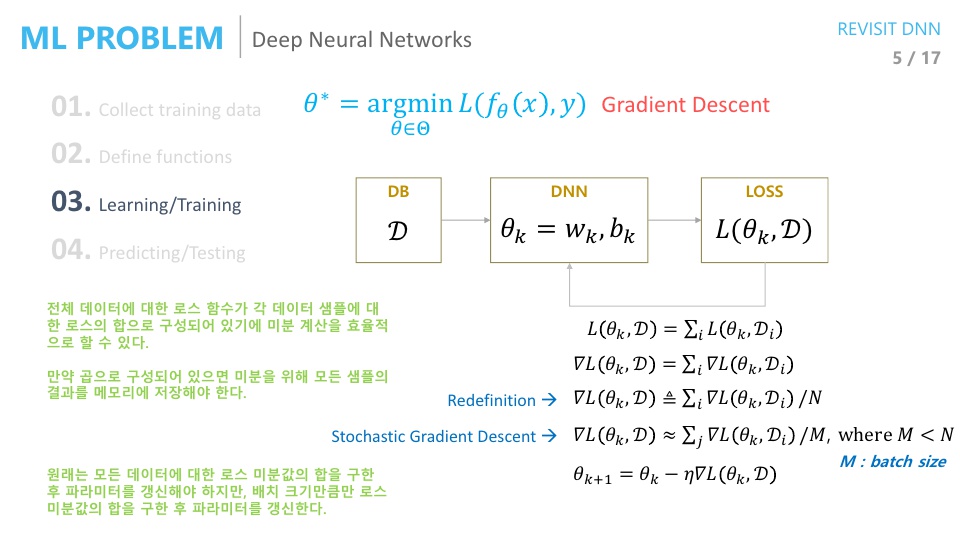
그러면 전체 과정을 한번 보겠습니다. 먼저 \(\mathcal D\)라는 Training DB가 있고 \(\theta_{k}\) 라는 현재 파라미터가 있다고 가정해 봅시다.
이 때, Loss 함수를 거치고 \(\theta\)가 업데이트 되는 과정을 한번 살펴보겠습니다.
먼저 \(L(\theta_{k}, \mathcal D) = \sum_{i}L(\theta_{k}, \mathcal D_{i})\) 식의 뜻은 모든 training DB에 대한 loss function은 각 sample 별 loss function의 합과 같다는 뜻입니다.
그리고 위 식의 양변에 gradient를 취해주어 \(\nabla L(\theta_{k}, \mathcal D) = \sum_{i} \nabla L(\theta_{k}, \mathcal D_{i})\) 로 식을 만들어 줍니다.
이 때 우변을 \(N\) (DB의 크기) 으로 나누어 준다면 샘플 별 평균 Loss 크기값을 계산하게 되고 M(미니 배치의 크기)으로 나누게 되면 미니 배치 별 평균 Loss를 구할 수 있습니다.
미니 배치를 이용하는 것이 전체 데이터를 이용하는 것 보다 학습 속도에 장점이 있기 때문에 미니 배치를 사용하는 것이 좋습니다. 전체 DB를 이용해서 학습하게 되면 연산량이 상당히 커지고 모든 DB가 다 계산되어야 한번 업데이트 되기 때문에 학습 속도 또한 느려집니다.
이 때, 각 샘플별 Loss의 평균과 미니 배치 별 Loss 의 평균이 유사할 것이라 생각하고 미니 배치 별 Loss로 파라미터를 업데이트 해줍니다.
1번 업데이트 되는 것을 step 이라고 하고 모든 training DB를 한번 다 훑는 것을 epoch이라고 하면 1 epoch 당 1 step의 업데이트가 발생하는데 미니 배치를 사용하면 1epoch 당 N/M step의 업데이트가 발생하게 됩니다.

우리가 학습해야 할 네트워크의 구조가 딥 뉴럴 네트워크이기 때문에 학습해야 할 파라미터가 weight와 bias로 구성되어 있습니다.
그리고 이 weight와 bias는 layer 별로 존재하게 됩니다. 현대 딥 뉴럴 네트워크에서 사용하는 layer의 수는 엄청나게 많기 때문에 파라미터의 수 또한 엄청나게 많아집니다.
이 때 중요한 것은 엄청나게 많은 파라미터들을 업데이트 하기 위하여 Loss function을 미분을 해야 합니다.
즉, 각 layer 별 weight와 bias에 대하여 Loss function을 미분을 하여 그 값만큼 파라미터를 업데이트 하는 과정이 필요합니다.
이 과정이 엄청나게 복잡하기 때문에 딥 뉴럴 네트워크에 한번 암흑기가 왔지만 backpropagation을 통하여 극복해 내었습니다.

그러면 backpropagation에 대하여 알아보겠습니다.
backpropagation 알고리즘은 output layer에서 부터 먼저 error signal을 구합니다.
output layer의 error signal은 cost를 네트워크의 출력값으로 미분을 합니다.
그리고 \(⊙\)는 element-wise 곱을 뜻합니다. 그러면 output layer의 error signal과 activation function의 미분값을 element-wise 곱을 하면 output layer의 error를 구할 수 있습니다.
그리고 그 앞 layer와의 관계를 보고 \(\delta^{l+1}\)을 이용하여 \(\delta^{l}\) 을 계속 구해나아갈 수 있습니다. 이 때, \(\delta^{l+1}\) 을 이용하여 그 앞단의 \(\delta^{l}\)을 구하는 과정이므로 backpropagation이라고 부르게 됩니다.
위 과정을 통하여 각 layer에 대한 error signal을 구하였습니다. 우리가 궁금한 것은 각 layer별 bias와 weight에 대한 error signal 입니다.
이 때, bias에 대한 error signal은 각 layer에 대한 error signal과 같고 weight에 대한 error signal은 layer의 입력으로 들어오는 값을 곱해주면 됩니다.
이 구하는 과정이 dynamic programming기법으로 결과 값이 계속 누적되어 효율적으로 계산되므로 빠르게 weight와 bias에 대한 미분값을 구할 수 있습니다.

그러면 backpropagation에서 loss function으로 주로 사용하는 Mean Square Error와 Cross Entropy에 대하여 알아보려고 합니다.
앞에서 설명하였듯이 loss function으로 두 가지를 사용하는 이유는 backpropagation알고리즘에 대한 다음 두 가지 가정을 만족하는 함수 이기 때문이었습니다.
- 조건1 : 전체 데이터셋에 대한 Loss는 각각의 데이터의 Loss의 합과 같다.
- 조건2 : Loss를 구성할 때, 네트워크의 출력값 만을 사용한다.
그러면 어떨 때, Mean Square Error를 쓰고 어떨 때에는 Cross Entropy를 쓰는 것이 좋은지 한번 살펴보도록 하겠습니다.
이 비교를 하기 위해서는 2가지 관점에서 비교를 할 수 있습니다.
- 1번째 관점 : Backpropagation
- 2번째 관점 : Maximum Likelihood
결과적으로는 Backpropagation 관점에서는 Cross Entropy가 좋습니다.
두번째로 Maximum Likelihood 관점에서 만약 출력 값이 Continuous한 값이라면 Mean Square Error를 쓰는 것이 좋고 Discrrete한 값이면 Cross Entropy를 쓰는 것이 낫다고 할 수 있습니다.
그러면 첫번째로 Backpropagation이 잘 동작하는 관점에서 살펴보도록 하겠습니다.
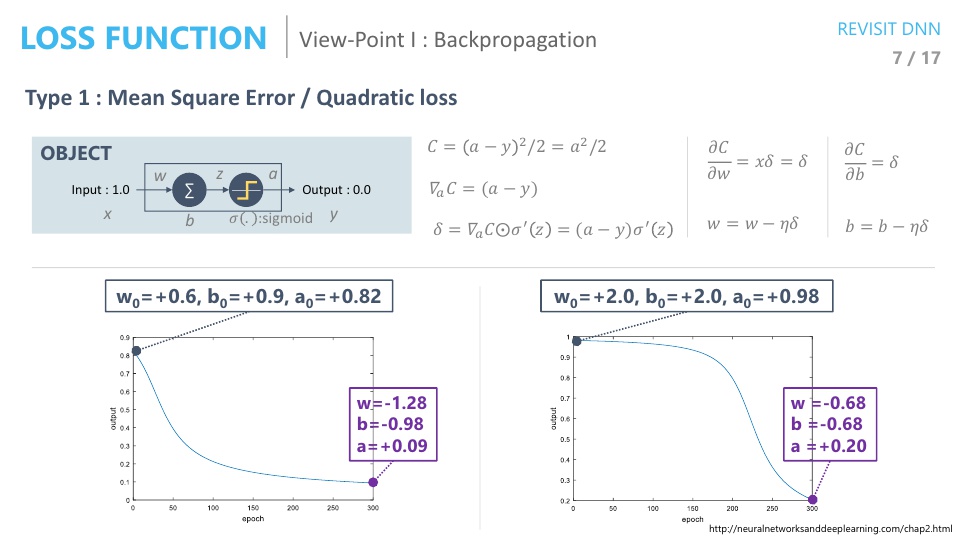
위 슬라이드와 같이 아주 간단한 뉴럴 네트워크를 한번 살펴보도록 하겠습니다. 입력이 1이면 출력이 0이고 노드는 딱 1개 입니다.
- 입력이 들어가면 w를 곱하고 b를 더하고 activation을 거칠 때, 시그모이드를 거칩니다.
위 조건으로 backpropagation 알고리즘을 사용해 보겠습니다.
Loss function으로 Mean Square Error를 사용한다는 것은 입력과 출력의 차이의 제곱으로 하는 것을 뜻합니다.
- 즉, \(C = (a - y)^{2} / 2 = a^{2} / 2\)가 됩니다. 여기서 \(a\)는 네트워크의 출력입니다.
backpropagation을 하기 위하여 그 다음 과정은 네트워크의 출력값으로 미분을 합니다.
- 즉, \(\nabla_{a} C = (a - y)\)가 됩니다.
그 다음으로 이전 입력값인 activation을 미분을 해서 element-wise 곱합니다.
- 즉, \(\delta = \nabla_{a} C ⊙ \sigma'(z) = (a - y)\sigma'(z)\)이 됩니다.
그 다음으로 \(w\)에 대하여 미분을 해줍니다. 앞의 과정까지 포함해서 식으로 표현하면 다음과 같습니다.
- 즉, \(\frac{\partial C}{\partial w} = x \delta = \delta\) 왜냐하면 입력값 \(x\)가 1이기 때문입니다.
그러면 이 값으로 최종 weight를 업데이트 해주면 \(w = w - \eta \delta\)가 됩니다.
bias에 대해서도 위와 같은 과정을 거치면 \(\frac{\partial C}{\partial b} = \delta\)가 되어 \(b = b - \eta \delta\)가 됩니다.
이제 학습에 필요한 수식이 모두 준비가 되었습니다. 그 전에 위 슬라이드의 그래프를 한번 보겠습니다.
위 좌, 우 그래프를 보면 초기값의 차이에 따라서 output의 차이가 있는 것을 볼 수 있습니다. 초기값이 왜 결과에 영향을 미칠까요?

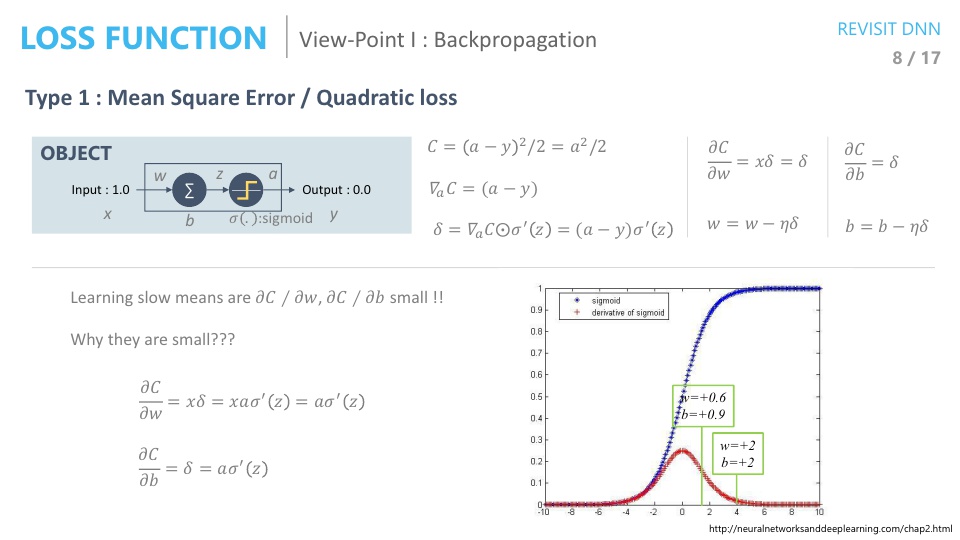
backpropagation을 보면 activation function의 미분값이 항상 들어가 있습니다.
학습에 차이가 있다는 것은 \(w, b\)에 대한 변화가 제대로 이루어 지지 않았다는 뜻입니다. \((\partial C / \partial w), (\partial C / \partial v)\)에 대하여 살펴보겠습니다.
먼저 \(\frac{\partial C}{\partial w}, \frac{\partial C}{\partial b}\) 모두 \(\sigma'(z)\)가 포함되어 있습니다.
여기서 \(\sigma(z), \sigma'(z)\)의 값 분포를 보면 오른쪽 그래프와 같은데, 초기값에 따라서 \(\sigma'(z)\)의 값이 0에 수렴해 버릴 수도 있습니다.
즉, 앞 장에서 보면 \(w = 2, b = 2\) 일 때의 결과가 안좋았었는데, 그 이유는 gradient가 0에 가까워서 변화량이 너무 작은 상태에서 시작했기 때문이었습니다.
- 앞 장의 슬라이드를 보면 \(w = 2, b = 2\)인 상태에서는 변화량이 조금씩 조금씩 있다가 어느 순간 부터 학습 되기 시작하는 그래프를 확인할 수 있습니다.
- 반면 \(w = 0.6, b = 0.9\)인 상태에서는 처음부터 gradient가 커서 변화가 잘 되었기 때문에 결과가 좋았다고 볼 수 있습니다.
특히, sigmoid activation 같은 경우에는 gradient의 최댓값이 1/4 이기 때문에 layer가 거듭될수록 최소 1/4 만큼씩 줄어들어서 변화량이 급격하게 줄어들어 입력층에 가까울수록 변화가 없게 됩니다.
- 이 문제가 gradient vanishing 문제입니다.
따라서 이런 문제를 해결하기 위해 ReLu actication을 사용 합니다. \(\text{Relu} = \text{max}(0, x)\)로 음수는 모두 0으로 만드는 반면 양수는 그대로 통과 시킵니다.
- 즉, 양수의 경우 gradient가 1이므로 입력층과 가까운 레이어에도 gradient가 전달될 수 있습니다.

위 식은 Cross Entropy에 대한 gradient값을 계산하는 과정입니다.
결과를 보면 Mean Square Error 때와는 다르게 \(\sigma'(z)\)의 값이 곱해지지 않는 것을 알 수 있습니다.
즉, backpropagation할 때, 레이어가 깊어질수록 값이 줄어드는 것을 개선할 수 있고 초기값에 둔감하게 학습할 수 있습니다.

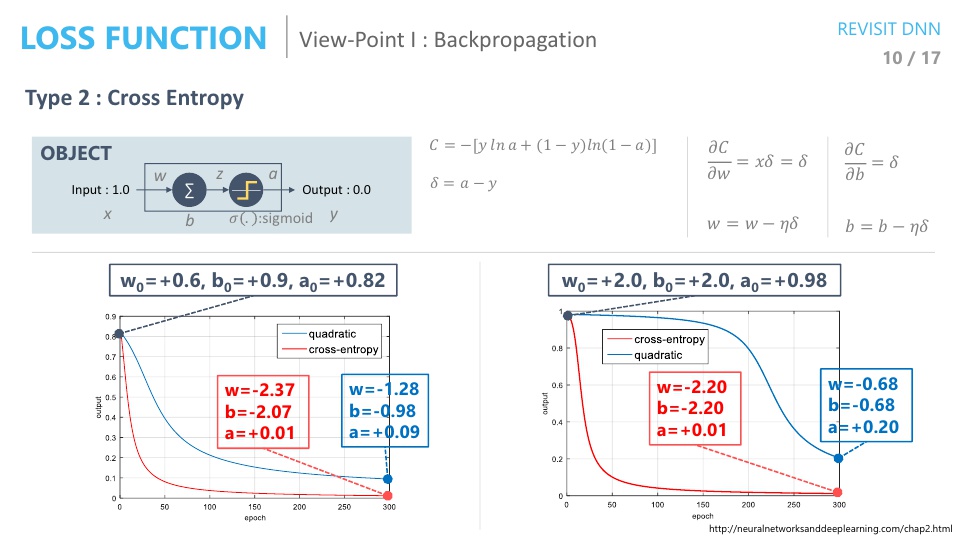
따라서 Cross Entropy를 사용하는 경우 초기값이 학습에 영향을 끼치는 것을 둔감화 시킬 수 있고 학습이 둘 다 잘되는 것을 알 수 있습니다.
정리하면, backpropagation 관점에서는 Cross Entorpy를 (MSE 대신)Loss function으로 사용하는 것이 더 유리하고 그 이유는 학습할 때, \(\sigma'(z)\) 항이 없기 때문에 더 깊은 레이어 까지 학습이 가능하기 때문입니다.

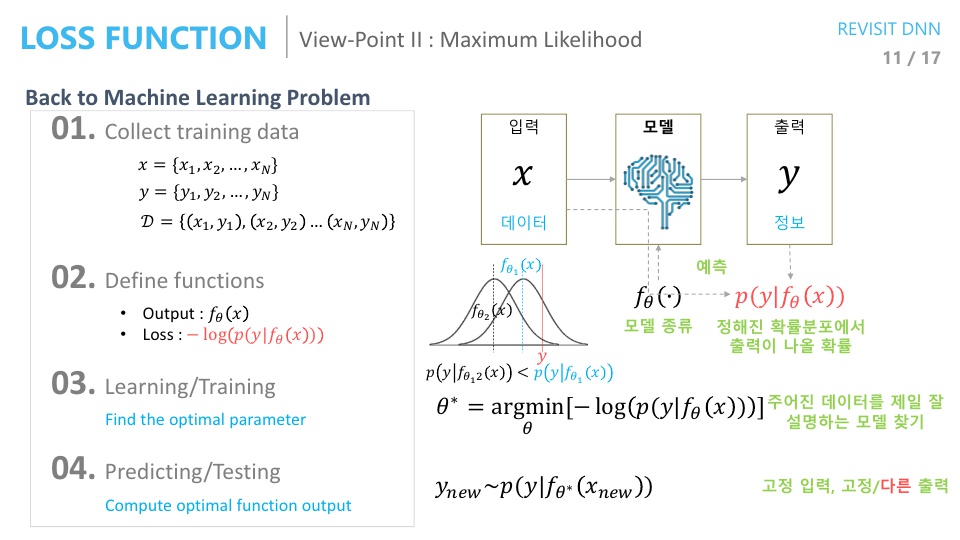
이번에는 Maximum Likelihood 관점에서 Loss function을 살펴보도록 하겠습니다.
네트워크의 출력 값인 \(f_{\theta}(x)\)가 정답 \(y\)와 가까워지도록 하는 것이 학습의 목표입니다. 따라서 두 값이 다른 정도를 Loss function으로 두고 문제를 풀었습니다.
이것을 다른 관점인 “네트워크의 출력값이 있을 때, 우리가 바라는 정답이 발생할 확률이 높길(최대) 바라는 것”이라는 관점으로 살펴보려고 합니다. 즉, Maximum Likelihood 관점으로 살펴보면 다음과 같습니다.

\[p(y \vert f_{\theta}(x))\]

이 관점에서 문제를 바라보려면 2가지 가정이 필요합니다.
- 먼저, 딥 뉴럴 네트워크 모델이 어떤 모델을 가지느냐 입니다. (사실 이것은 Backpropagation에서도 쉬운 구조를 가정했었습니다.)
- 또 한가지 추가되는 것은 확률 분포에 대한 likelihood가 최대화가 되도록 하고 싶으므로 이 확률 분포 모델을 미리 정해주어야 합니다. 예를 들면, 가우시안 분포인지, 베르누이 분포인지 등등…
확률 분포는 가우시안 분포임을 가정하고 진행해 보겠습니다.
이 가정 속에서 보면 네트워크의 출력은 확률 분포를 정의하기 위한 파라미터 추정이라고 할 수 있습니다.
- 가우시안 분포라고 가정하였기 때문에, 여기서 추정하는 파라미터는 예를 들어 평균값이라고 할 수 있습니다. (편의를 위하 표준 편차는 무시하겠습니다.)
그러면 위 슬라이드의 그래프처럼 출력값이 \(f_{\theta_{1}}(x), f_{\theta_{2}}(x)\)일 때에 따라서, 다른 분포를 그릴 수 있습니다.
위 그래프에서 정답인 \(y\) 값은 고정된 값입니다.
이 때 우리가 살펴볼 관점이 Maximum Likelihood이고 추정하는 파라미터는 평균이기 때문에, 평균에 해당하는 값(확률 최댓값)이 \(y\)와 최대한 가까워 지길 원합니다.
- 관점만 다를 뿐 backpropagation일 때와 같은 내용을 다루는 것이 backpropagation에서는 네트워크 출력값과 정답값이 같기를 바라는것이고
- maximum likelihood 관점에서는 추정하는 파라미터 값의 확률 분포에서 확률이 최대가 되는점(최대 가능도)과 정답값이 같기를 바라는 것입니다.
이 문제를 풀기 위해서 Negative log likelihood를 최소화 하는 파라미터를 찾는 문제로 형태를 바꾸겠습니다.
- 그러면 솔루션인 \(\theta^{*} = \operatorname*{argmin}_\theta[-log(p( y \vert f_{\theta}(x)))]\) 가 됩니다.
- 즉, 이 문제의 솔루션인 \(\theta^{*}\)는 뜻이 \(\theta^{*}\)로 확률 분포를 그렸을 때, 가장 확률이 높은 평균점이 정답값 \(y\)와 가장 가깝다는 의미입니다.
이렇게 해석하였을 때의 장점은 확률 분포 모델을 찾았기 때문에 고정 입력 값에 고정 출력이 아닌 샘플링을 통한 다른 출력을 낼 수 있습니다. (이 내용은 이후에 오토인코더와도 연관되어 있습니다.)

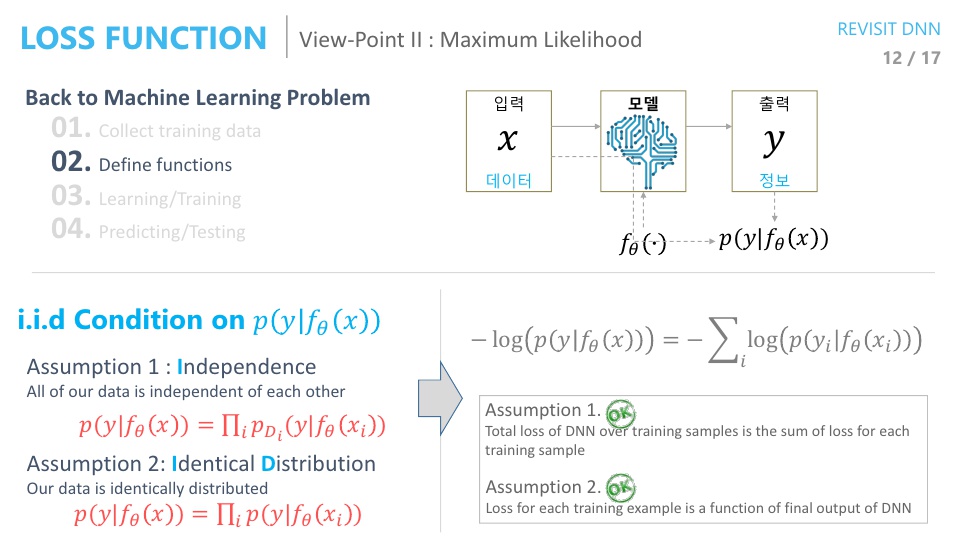
앞에서 사용한 Negative log likelihood가 i.i.d 조건을 만족시키는 지 한번 살펴보겠습니다.
먼저 Independence 조건은 다음 식을 통해 만족함을 보입니다.

\[p(y \vert f_{\theta}(x)) = \prod_{i} \ p_{D_{i}} (y \vert f_{\theta}(x_{i}))\]

즉, 각각의 샘플에 대한 확률이 독립적이므로 그 값들을 모두 곱한 것에 대한 확률은 데이터 전체에 대한 확률과 동일합니다.
두번째 조건인 Identical distribution은 각 샘플에 대한 확률 분포가 모두 동일한 확률 분포를 이용한다는 전제입니다. (즉, 샘플별로 확률 분포가 다르지 않다는 것입니다.)
이 두 조건을 모두 만족하기 때문에 \(-log(p(y \vert f_{\theta}(x))) = -\sum_{i} log(p(y_{i} \vert f_{\theta}(x_{i})))\)식을 만족하게 됩니다.

(위 슬라이드는 일변수 함수에 대한 식을 푼 것입니다.)

따라서 이전 슬라이드의 Negative log likelihood를 가우시안 분포와 베르누이 분포 각각에 대하여 최소화 되도록 풀면
- 가우시안 분포 : Mean Square Error로 정리가 되고
- 베르누이 분포 : Cross Entropy로 정리가 됩니다.
- 물론 \(-log(p(y_{i} \vert f_{\theta}(x_{i})))\)에서 \(f_{\theta}(x_{i})\)에 대한 확률 분포가 가우시안 또는 베르누이 라고 가정한 것입니다.
해석하면 우리가 생각하는 네트워크 출력값에 대한 확률 분포가 가우시안 분포에 가깝다고 생각이 들면 Mean Square Error를 사용하는 것이 낫다고 해석할 수 있고
반대로 네트워크 출력값이 베르누이 분포를 따른다고 생각이 들면 Cross Entropy를 쓰는 것이 낫다고 해석할 수 있습니다.
이 때, continuous한 값은 주로 가우시안 분포를 따른 다고 가정해서 Mean Square Error가 좋다고 해석한 것이고
반대고 discrete한 값은 베르누이 분포를 따르 다고 가정해서 Cross Entropy가 좋다고 해석한 것입니다.

(위 슬라이드는 다변수 함수에 대한 식을 푼 것입니다.)

마지막으로 Maximum Likelihood 관점에서 해석을 할 때, 네트워크의 출력값이 likelihood값이 아니라는 것을 다시 상기시키고 가겠습니다.
사전에 확률 분포를 가정하였었고 그 확률 분포를 규정짓는 파라미터를 추정하는 것입니다.

벤지오 교수의 Log likelihood for Neural Net 해석을 한번 보겠습니다.
Estimating a conditional probability \(P(Y \vert X)\)
- 조건부 확률 \(P(Y \vert X)\)를 추정해 보려고 합니다. 이 때, \(Y\)는 정답값이고 \(X\)는 네트워크의 출력값 입니다.
Parametrize it by \(P(Y \vert X) = P(Y \vert w = f_{\theta}(X))\)
- 여기서 네트워크의 출력 \(X\)는 확률 분포인데 그 확률 분포를 결정 짓는 파라미터 \(w\)에 의해서 최종 조건부 확률이 결정되어 집니다.
- 즉, 파라미터가 출력이 됩니다.
Loss = \(-log P(Y \vert X)\)
- 여기서 loss는 backpropagation을 사용해야 하기 때문에 -log를 붙여서 계산합니다.
E.g. Gaussian Y, \(w = (\mu, \sigma)\), typically only \(\mu\) is the network output, depends on \(X\)
- 여기서 확률 분포를 가우시안이라고 가정해 보면 평균과 분산 의 파라미터를 가지게 됩니다.
Equivalent to MSE criterion : \(\log{P(Y \vert X)} = \log{\sigma} + \Vert f_{\theta}(X) - Y \Vert^{2} / \sigma^{2}\)
- 가우시안 분포로 가정해서 negative log likelihood를 최소화 하면 MSE가 됩니다.
Multinoulli Y for classification : \(w_{i} = P(Y = i \vert x ) = f_{\theta, i}(X) = \operatorname*{softmax}_{i} (a(X))\), Loss = \(-log(w_{Y}) = -log(f_{\theta, Y}(X)\)
- 베르누이 분포(멀티누이 분포)로 가정해서 negative log likelihood를 최소화 하면 Cross Entropy가 됩니다.

지금까지 다른 Loss function은 Mean Square Error와 Cross Entropy가 있는데, 각 Loss function을 사용하여 학습 시키는 것을 해석을 할 때, 한 경우는 가우시안으로 다른 한 경우는 카테고리컬한 것으로 생각할 수 있었습니다.
이것을 오토인코더와 연관을 시켜보려고 합니다. 오토인코더는 네트워크의 입력이 \(x\)이고 출력도 입력과 같이 \(x\)이길 바라는 것이고 배리에이셔녈 오토인코더에서는 조건부 확률이 없고 단지 트레이닝 DB의 확률 분포 그 자체를 추정을 하게 됩니다.