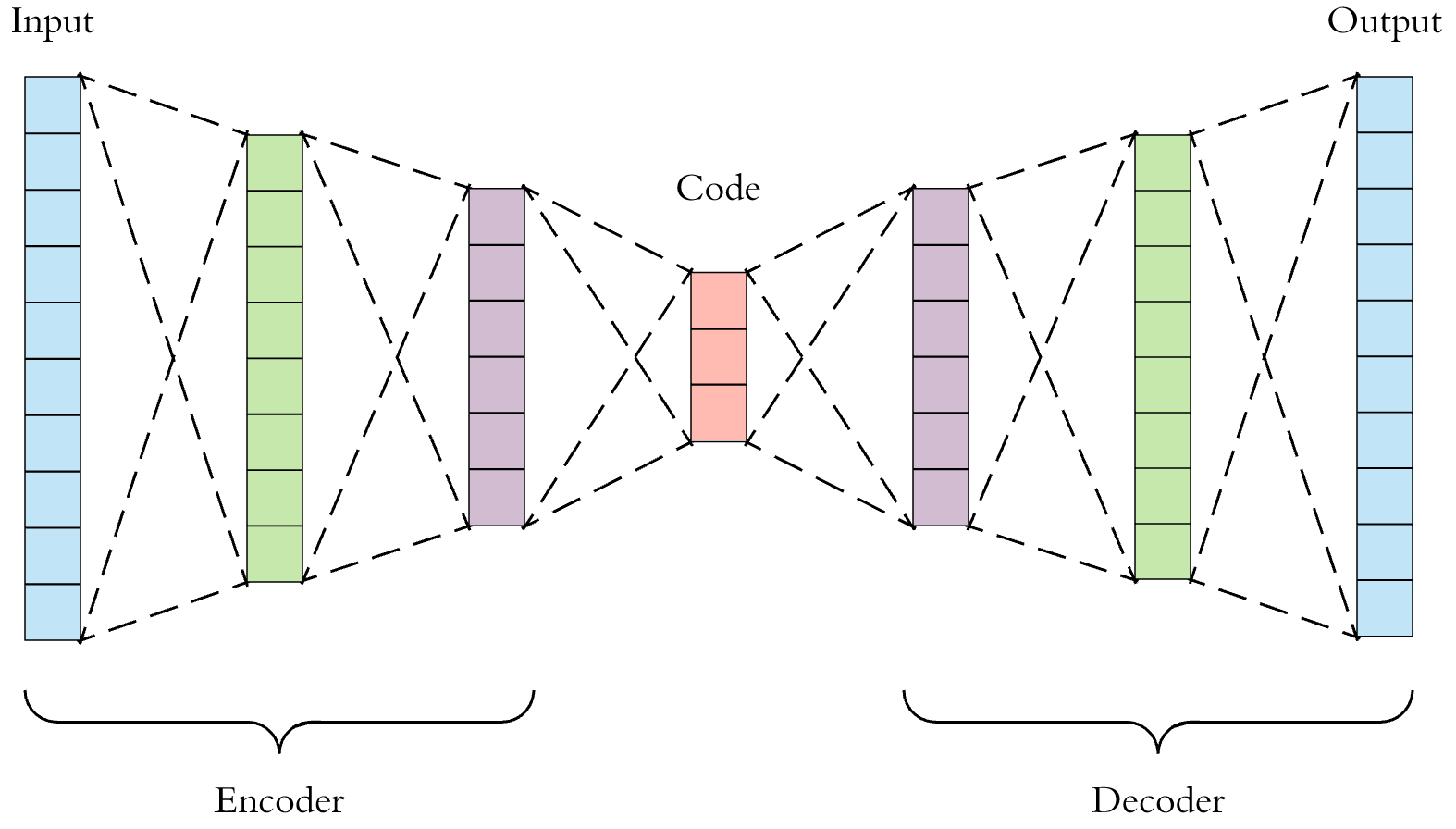
AutoEncoder의 모든것 (2. Manifold Learning)
2019, Feb 25
- 이 글은 오토인코더의 모든것 강의를 보고 요약한 글입니다.

- 이번 글에서는
manifold learning이 무엇인지 직관적으로 한번 알아보도록 하겠습니다.

- 이미지 데이터의 경우 상당히 큰 차원의 데이터를 가지고 있습니다. 예를 들면 256 x 256 사이즈의 RGB 데이터 라면 196,608(256 x 256 x 3)의 차원을 가지고 있습니다.
- manifold learning의 한가지 역할 중 하나는 차원 축소 인데, 굉장히 큰 차원을 저차원으로 줄일 수 있는 역할을 합니다.
- 위 슬라이드의 예를 들어 고차원(시각화를 위해 3차원으로 표현되어 있습니다.)을 저차원(2차원)으로 매핑 시키는 것을 한번 살펴보겠습니다.
- 그러면 먼저 매니폴드에 대한 정의를 먼저 살펴보도록 하겠습니다.
- 공간상에 데이터들을 표현하면 각 데이터들은 점의 형태로 찍혀질 것입니다. 매니폴드는 이런 점들을 최대한 에러 없이 아우를 수 있는 서브 스페이스라고 정의할 수 있습니다.
- 이 매니폴드를 잘 찾는 것이 매니폴드 러닝이라고 할 수 있고 잘 찾은 매니폴드를 저차원에 프로젝션 하면 저차원으로 차원 축소를 할 수 있는 것입니다.
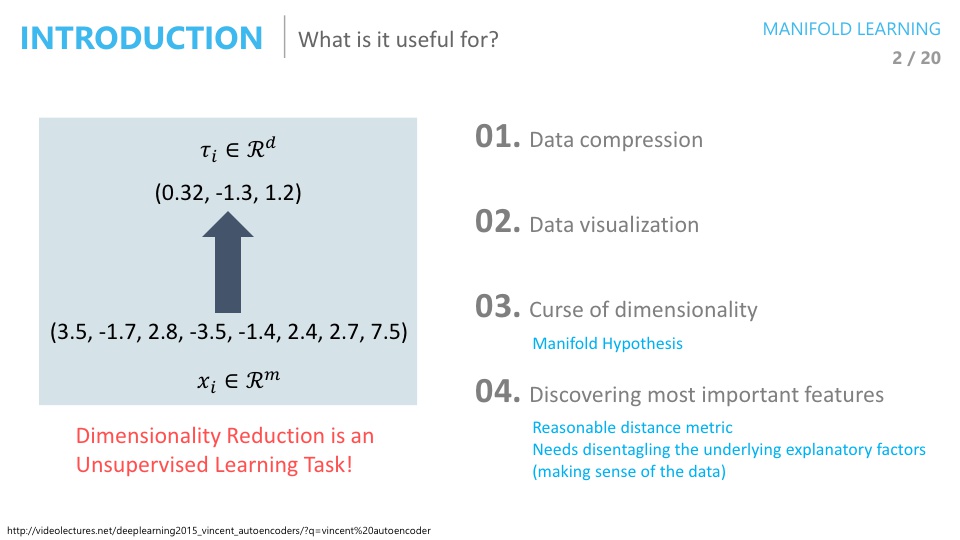
- 미니폴드 러닝은 간단하게 높은 차원의 데이터를 저 차원으로 잘 줄이고 싶은 것입니다.
- 특히 원래 데이터의 특성을 잘 유지하면서 차원을 축소해야 하는 작업니다.
- 이렇게 차원을 축소한 결과는 크게 4가지 용도로 사용될 수 있습니다.
- Data compression
- Data visualization
- Curse of dimensionality 개선
- Discovering most important features
- 먼저 Data compression과 관련된 내용부터 살펴보겠습니다.
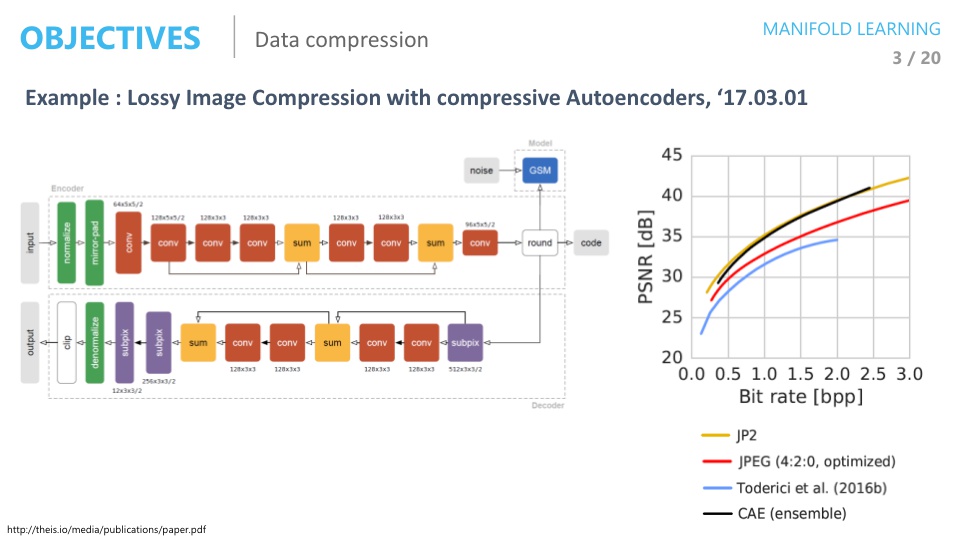
- 위 논문은 데이터 압축과 관련된 논문입니다.
- 사진 압축에 많이 사용되는 것 중 하나가 JPEG인데 JPEG과 비교하여 데이터 압축이 잘 되었다는 내용의 논문입니다.
- 입력의 이미지를 차원 축소 하여 저차원의 데이터(저용량의 데이터)를 가지고 있으면 다시 복원하여 사용할 수가 있습니다.
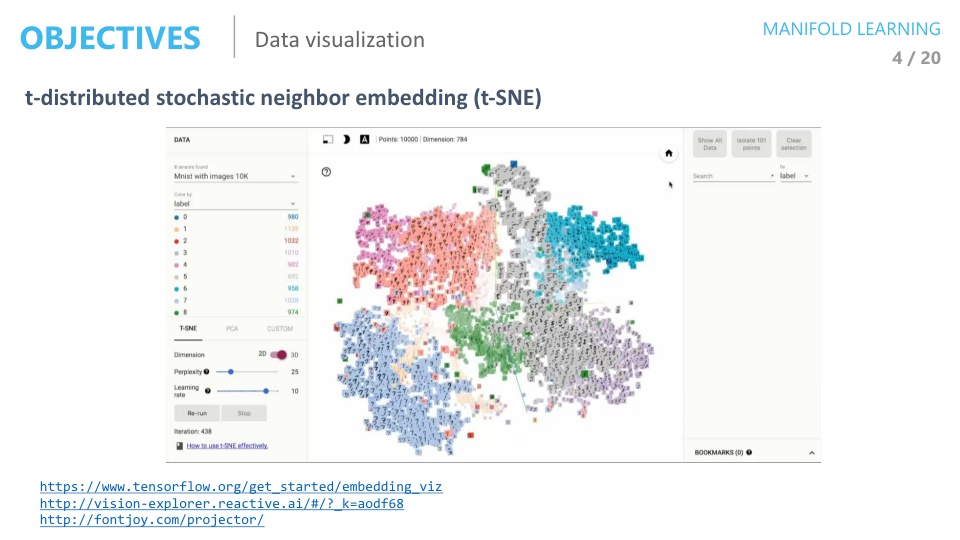
- 두번째 사용처인 Visualization은 위 슬라이드의 예제와 같습니다.
- 위 슬라이드 예제는
t-SNE방법으로 가장 많이 사용하는 Visualization 방법 중 하나입니다.
- 그 다음이
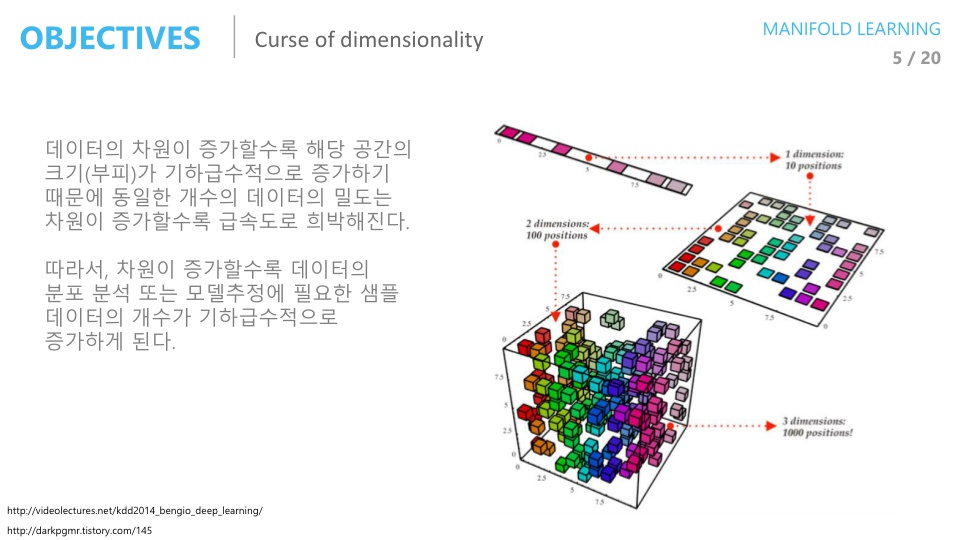
차원의 저주입니다. - 차원의 저주는 차원이 높아질수록 공간이 커지는 반면에 데이터의 수는 고정되어 있어 데이터의 밀도가 희박해 지는 문제를 뜻합니다.
- 예를 들어 1차원 총 공간이 10이고 데이터가 8이였으면 전체 공간에 80%만큼 데이터가 채워져 있었지만 2차원으로 늘어나면 전체 공간 100에서 8이므로 8% 공간만 차지하게 되고 3차원, 4차원으로 늘어날수록 그 비율은 더 줄어 들게 되는 문제입니다.
- 이렇게 전체 공간에 비하여 데이터가 너무 작아지면 분석 자체가 어려워져서 성능이 나빠지게 됩니다.

- 위와 같이 고차원의 밀도는 낮지만 이들의 집합을 포함하는 저차원의 매니폴드를 찾으면 이 매니폴드 상에서는 데이터의 밀도가 높게 나타나 집니다.

- 아주 고차원의 이미지 데이터에서는 균등 분포로 데이터를 샘플링 한다면 의미 있는 데이터를 얻을 수 없을 것입니다.
- 그 의미는 이미지 데이터 자체가 균등하게 공간상에 존재하는 것이 아니라 이미지 유형에 따라서 공간에 밀집되어 있다는 것을 뜻합니다.
- 균등 분포를 통해서 데이터를 샘플링 하면 노이즈 같은 이미지가 생기지만 어떤 공간에는 얼굴 이미지가, 어떤 공간에는 글씨가 있을 수 있습니다.
- 만약 얼굴 이미지를 잘 아우르는 매니폴드를 찾았다면 얼굴 이미지 간의 관계성 및 확률 분포를 찾을 수가 있고 그 확률 분포에서 샘플링을 한다면 없는 얼굴 이미지 데이터를 만들어 낼 수도 있습니다.
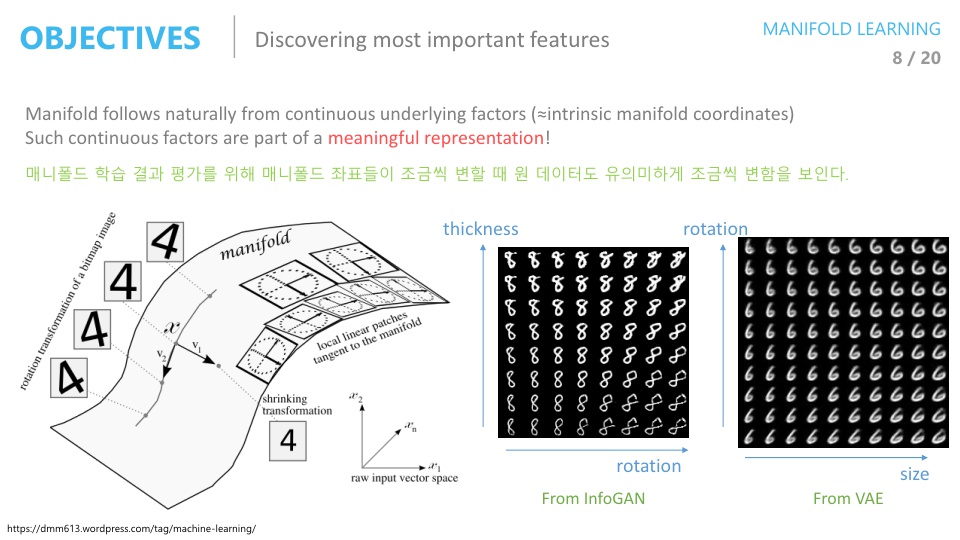
- 가장 많이 사용되는 매니폴드 러닝의 역할 중 마지막으로 언급하려는 것은 가장 중요한 feature를 찾는 것입니다.
- 위 슬라이드의 MNIST 이미지는 28 x 28 크기로 784 차원을 가지는 데 여기서 데이터를 잘 아우르는 매니폴드를 찾는다면 그 매니폴드에는 이미지의 회전, 변형, 두께등의 유의미한 feature가 있을 수 있습니다.
- 이러한 feature들은 자동으로 찾아지는데 그 이유는 Unsupervised learning으로 학습되어 지기 때문입니다.
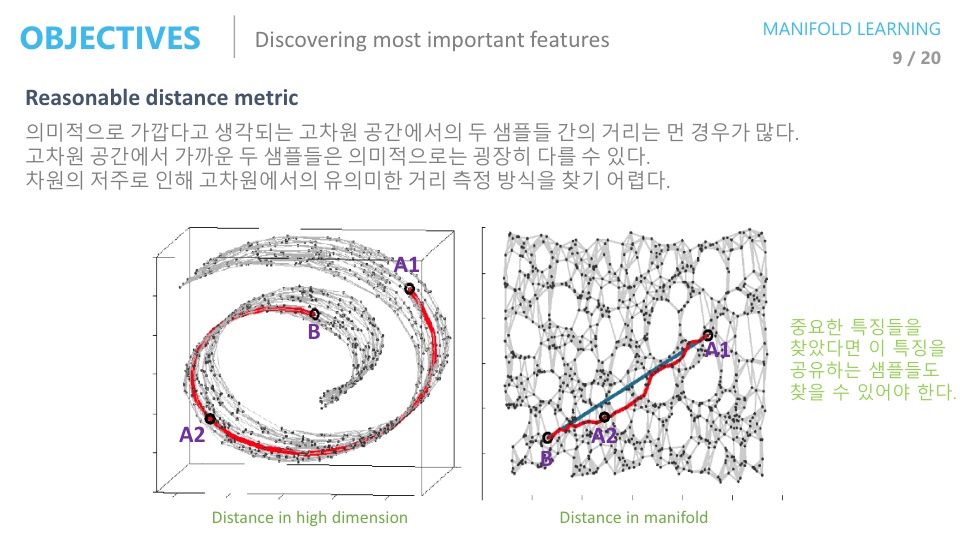
- 또한 매니폴드를 잘 찾으면 의미적으로 가까운 데이터들을 찾을 수 있습니다.
- 왼쪽의 고차원 데이터에서는 유클리디안 거리로 A1은 B와 가깝지만 매니폴드상에서의 거리를 오른쪽에서 보면 A1은 A2와 가깝습니다.
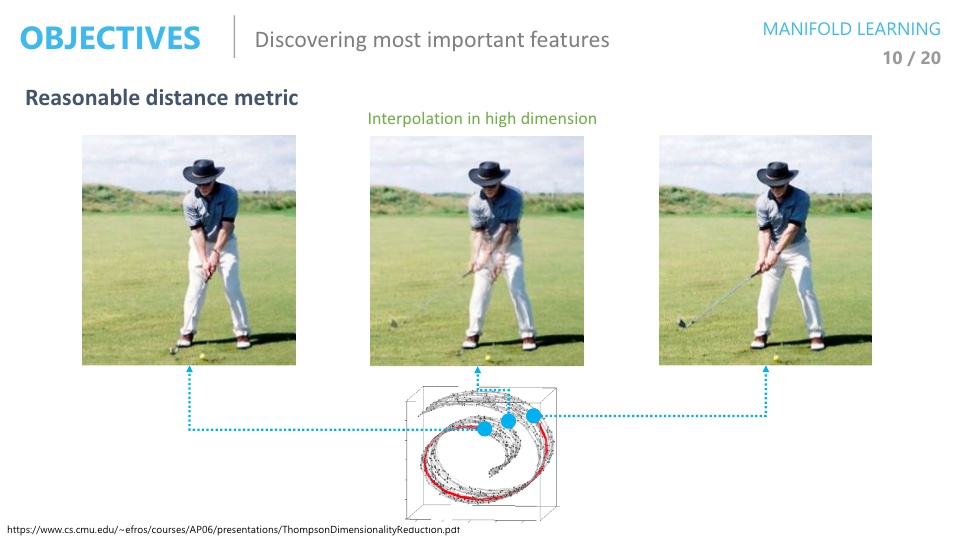
- 만약에 위 그림처럼 고차원 상에서 매니폴드의 두 점의 유클리단 거리로 가운데 점을 찾는다면 매니폴드위에 없는 데이터가 선택될 수 있고 그 데이터를 보면 의미 없는 데이터 일 수 있습니다.
- 위 슬라이드의 가운데 이미지를 보면 팔이 여러개인 의미 없는 데이터임을 알 수 있습니다.
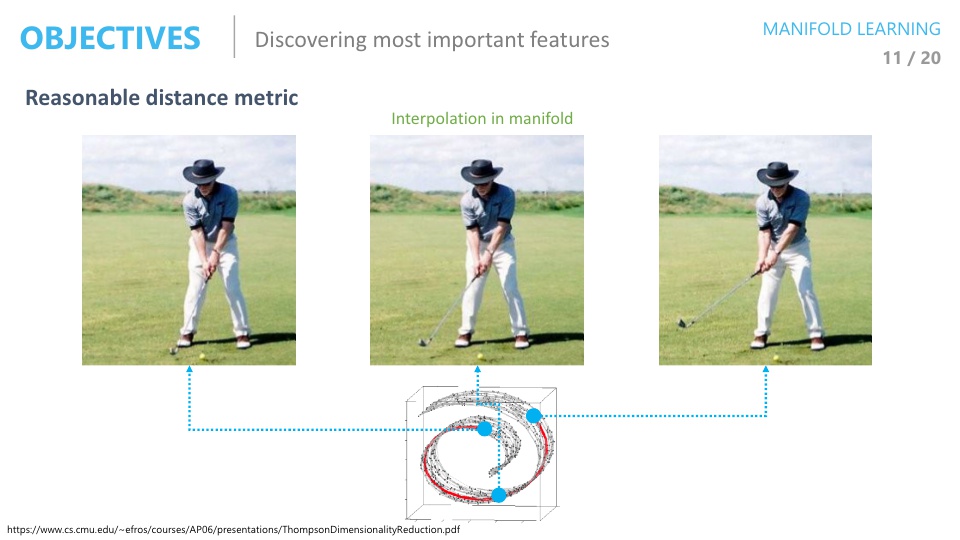
- 하지만 매니폴드 상에서 가운데 이미지를 찾는 다면 기대하는 의미가 있는 이미지가 나올 수도 있습니다.
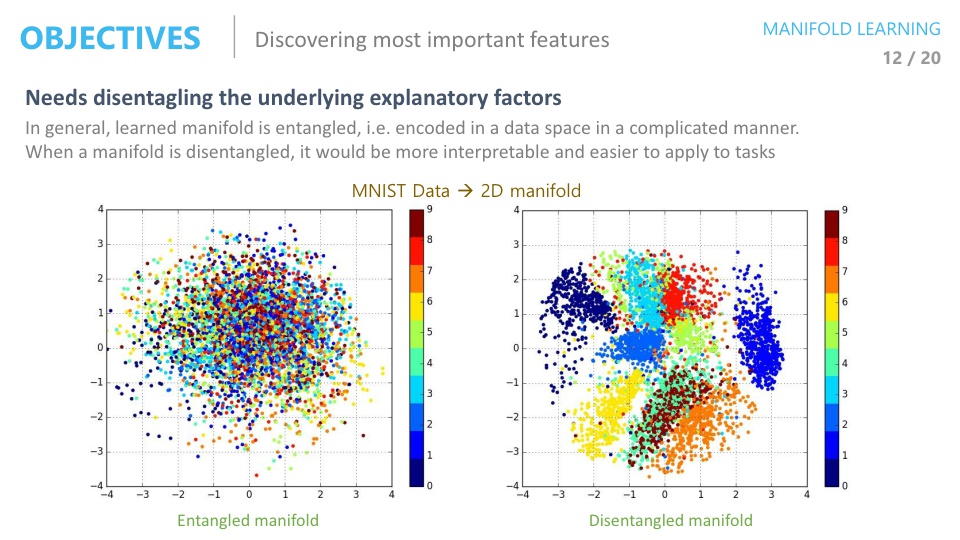
- 잘 학습된 매니폴드 에서는 오른쪽 이미지와 같이 Disentangled 형태를 가지게 됩니다.
- 위 그래프는 0 ~ 9 까지의 숫자 이미지를 2차원으로 차원 축소한 다음에 그래프상에 표시한 것인데 오른쪽 같이 숫자별로 군집되어 있어야 유의미한 feature로 매니폴드가 만들어 졌다고 할 수 있습니다.

- 그러면 오토인코더의 역할 중 하나인
차원 축소에 대하여 자세히 알아보려고 합니다. - 차원 축소를 하는 방법에는 위와 같이 Linear한 방법 또는 Non-linear한 방법이 있습니다.
- 오토인코더와의 비교를 위하여 위에서 소개된 방법들을 간략하게 알아보고 가겠습니다.