딥러닝 Backpropagation 정리

2019, Jun 29    

deep learning 관련 글 목록

• 딥러닝의 backpropagation 관련 내용과 자주 사용되는 식들의 미분값에 대하여 정리해 보겠습니다.

목차

• sigmoid

• binary cross entropy

• binary cross entropy with sigmoid

• softmax

• cross entropy with softmax

• multi layer perceptron

• multi layer perceptron with multiclass

• convolution

• zero padding

• pooling

• relu

• transposed convolution

• conv1d example

sigmoid

• sigmoid 함수의 정의는 다음과 같습니다.

• \[\sigma(z) = \frac{1}{1 + e^{-z}} \tag{1}\]

• 식 (1)의 \(z\) 는 모델의 출력값에 해당합니다.
• sigmoid 함수의 미분 결과는 다음과 같습니다.

• \[\frac{d\sigma(z)}{dz} = \frac{d}{dz} (1 + e^{-z})^{-1} \tag{2}\]
• \[= (-1)\frac{1}{(1 + e^{-z})^{2}} \frac{d}{dz}(1 + e^{-z}) \tag{3}\]
• \[= (-1)\frac{1}{(1 + e^{-z})^{2}} (0 + e^{-z}) \frac{d}{dz}(-z) \tag{4}\]
• \[= (-1)\frac{1}{(1 + e^{-z})^{2}}e^{-z}(-1) \tag{5}\]
• \[= \frac{e^{-z}}{(1 + e^{-z})^{2}} \tag{6}\]
• \[= \frac{1 + e^{-z} - 1}{(1 + e^{-z})^{2}} \tag{7}\]
• \[= \frac{1 + e^{-z}}{(1 + e^{-z})^{2}} - \frac{1}{(1 + e^{-z})^{2}} \tag{8}\]
• \[= \frac{1}{(1 + e^{-z})} - \frac{1}{(1 + e^{-z})^{2}} \tag{9}\]
• \[= \frac{1}{(1 + e^{-z})}(1 - \frac{1}{(1 + e^{-z})} \tag{10}\]
• \[= \sigma(z)(1 - \sigma(z)) \tag{11}\]

• \[\therefore \frac{d\sigma(z)}{dz} = \sigma(z)(1 - \sigma(z)) \tag{12}\]

binary cross entropy

• binary cross entropy의 식은 다음과 같습니다.

• \[J = -y\ln{(p)} - (1-y)\ln{(1-p)} \tag {13}\]

• 위 식에서 \(y\) 는 정답에 해당 값이며 0 또는 1을 가집니다. \(p\) (predict)는 모델의 출력값을 나타냅니다.

• 식(13)의 binary cross entropy 함수의 미분 결과는 다음과 같습니다.

• \[\frac{dJ}{dp} = -\frac{y}{p} -\frac{1-y}{1-p}\frac{1-p}{dp} = -\frac{y}{p} + \frac{1-y}{1-p} \tag{14}\]

binary cross entropy with sigmoid

• 일반적으로 binary classification 같은 문제에서는 binary cross entropy와 sigmoid를 섞어서 사용합니다.
• 식 (13)의 \(p\) 가 모델의 최종 출력 \(z\) 에 sigmoid 함수를 적용한 \(\sigma(z)\) 라고 가정해 보겠습니다. 그러면 다음과 같이 식을 적을 수 있습니다.

• \[J = -y\ln{(p)} - (1-y)\ln{(1-p)} = -y\ln{(\sigma(z))} - (1-y)\ln{(1-\sigma(z))} \tag{15}\]

• 식 (15)를 \(z\)에 대하여 미분하기 위해 chain rule을 이용하여 나타내면 다음과 같습니다.

• \[\frac{dJ}{dz} = \frac{dJ}{dp}\frac{dp}{dz} \tag{16}\]

• 식 (16)에서 \(\frac{dJ}{dp}\) 의 결과는 식 (14)를 통해 구하였고 \(\frac{dp}{dz}\) 는 식 (12)를 통하여 구하였습니다. 따라서 다음과 같이 정리할 수 있습니다.

• \[\frac{dJ}{dz} = \frac{dJ}{dp}\frac{dp}{dz} = (-\frac{y}{p} + \frac{1-y}{1-p})\sigma(z)(1 - \sigma(z)) \tag{17}\]
• \[= (-\frac{y}{\sigma(z)} + \frac{1-y}{1-\sigma(z)})\sigma(z)(1 - \sigma(z)) \tag{18}\]
• \[= \frac{-y + y\sigma(z) + \sigma(z) -y\sigma(z)}{\sigma(z)(1 - \sigma(z))}\sigma(z)(1 - \sigma(z)) \tag{19}\]
• \[= \frac{-y + \sigma(z)}{\sigma(z)(1 - \sigma(z))}\sigma(z)(1 - \sigma(z)) \tag{20}\]
• \[= \sigma(z) - y \tag{21}\]

• \[\therefore \frac{dJ}{dz} = \frac{-y\ln{(\sigma(z))} - (1-y)\ln{(1-\sigma(z))}}{dz} = \sigma(z) - y \tag{22}\]

softmax

• sofrmax의 식은 다음과 같습니다.

• \[p_{k} = \frac{e^{z_{k}}}{\sum_{i}e^{z_{i}}} \tag{23}\]

• 식 (23) 에서 \(p_{k}\) 는 인덱스 \(k\) 에 해당하는 출력의 확률값을 의미합니다. \(z_{k}\) 는 인덱스 \(k\) 의 출력을 의미합니다.
• 모든 출력에 대하여 exp를 적용하고 각 인덱스 \(i\) 에 대하여 전체에 대한 비율을 계산하므로 확률값 처럼 나타낼 수 있으며 모든 \(p_{k}\) 를 다 더하면 1이 됩니다.
• 식 (23)의 \(p_{k}\) 의 \(z_{k}\) 에 대한 미분값은 아래 식의 과정으로 구할 수 있습니다.
• 표기의 편의성을 위하여 \(\sum_{i}e^{z_{i}} = \Sigma\) 로 표기하겠습니다.

• \[\frac{\partial p_{k}}{\partial z_{k}} = \frac{\partial}{\partial z_{k}} \biggl( \frac{e^{z_{k}}}{\sum_{i}e^{z_{i}}} \biggr) \tag{24}\]
• \[= \frac{\mathbf{D} \cdot e^{z_{k}} \Sigma - e^{z_{k}} \cdot\mathbf{D} \Sigma}{\Sigma^{2}} \quad (\because \dfrac{f(x)}{g(x)} = \dfrac{g(x) \mathbf{D} f(x) - f(x) \mathbf{D} g(x)}{g(x)^2}) \tag{25}\]
• \[= \frac{e^{z_{k}}(\Sigma - e^{z_{k})}}{\Sigma^{2}} \quad(\because \mathbf{D}\Sigma= \mathbf{D} \sum_{i} e^{z_{i}} = e^{z_{k}}) \tag{26}\]
• \[= \frac{e^{z_{k}}}{\Sigma} \dfrac{\Sigma - e^{z_{k}}}{\Sigma} \tag{27}\]
• \[= p_{k}(1 - p_{k}) \tag{28}\]
• \[\therefore \frac{\partial p_{k}}{\partial z_{k}} = p_{k}(1 - p_{k}) \tag{29}\]

• 식 (29)인 softmax의 미분 결과와 식 (11)의 sigmoid 결과를 비교해보면 결과가 같은 것을 확인할 수 있습니다.

cross entropy with softmax

multi layer perceptron

multi layer perceptron with multiclass

convolution

zero padding

pooling

• pooling 연산은 대표적으로 average pooling과 max pooling을 사용합니다. 두가지 연산 방식에 대하여 출력부로 부터 흘러온 gradient를 어떻게 전파하는 지 살펴보면 다음과 같습니다.

average pooling

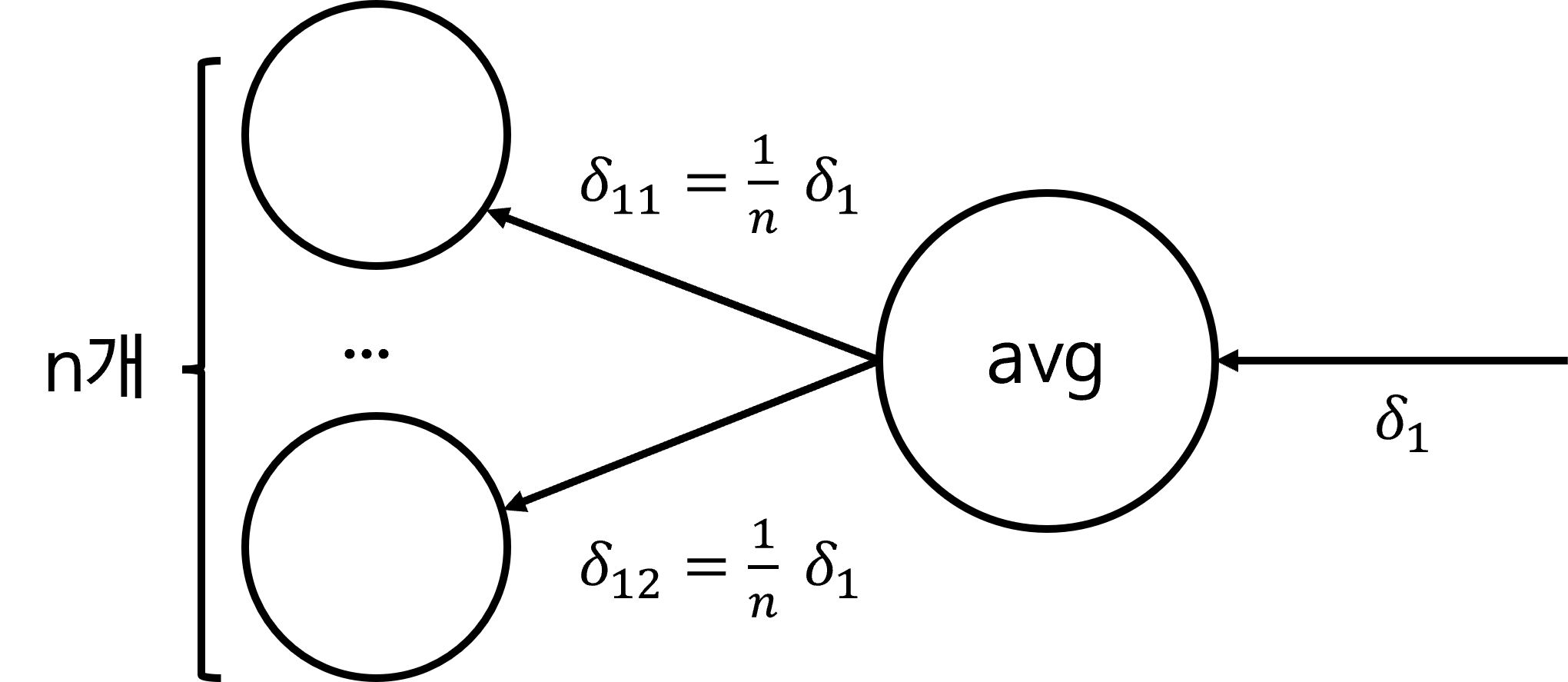
• 먼저 average pooling의 back propagation 시 동작은 위 그림과 같습니다.
• average pooling layer에 gradient가 전달되면 average pooling을 한 대상의 갯수 \(n\) 으로 나눈 값을 layer들로 전달합니다.

max pooling

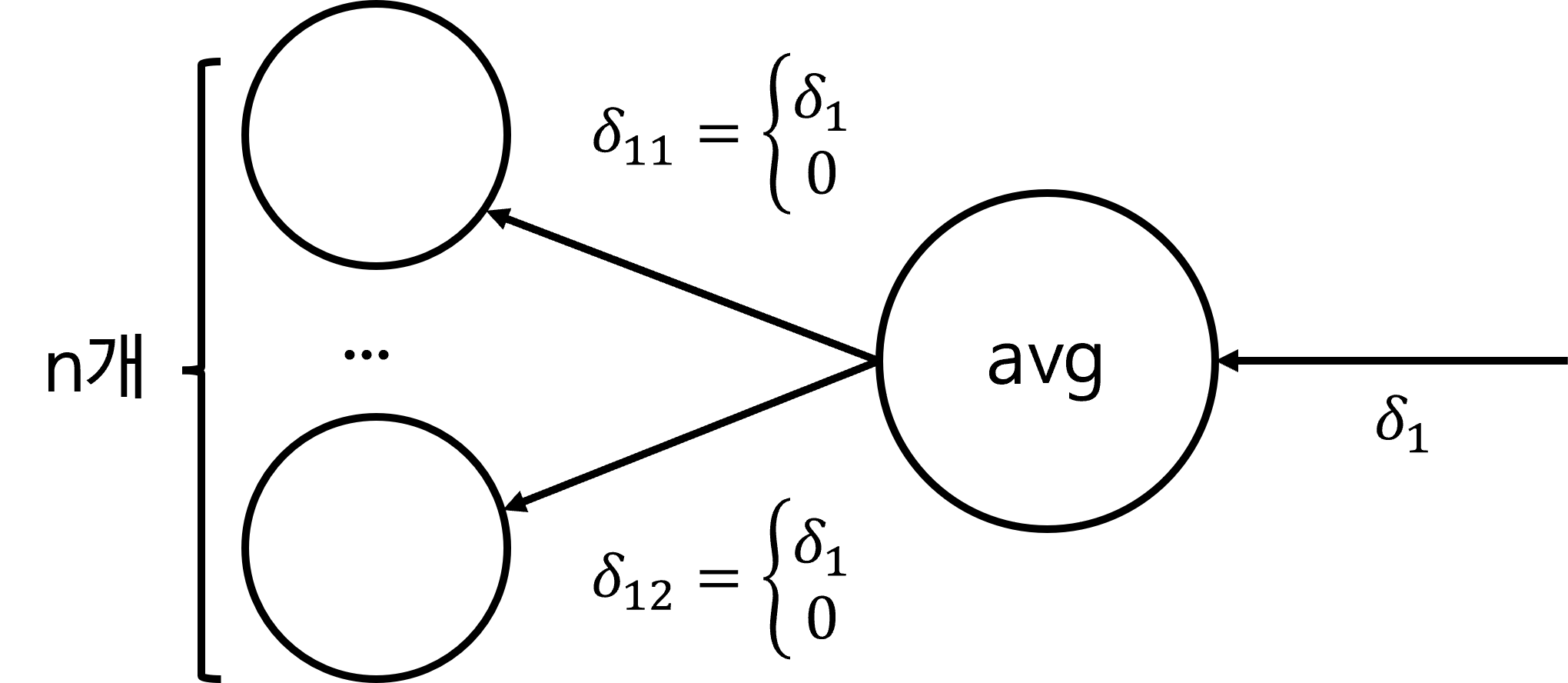
• max pooling의 경우 실제 최댓값에 해당하는 layer들 부분에만 gradient를 그대로 전달하고 나머지 layer는 0으로 전달합니다.

relu

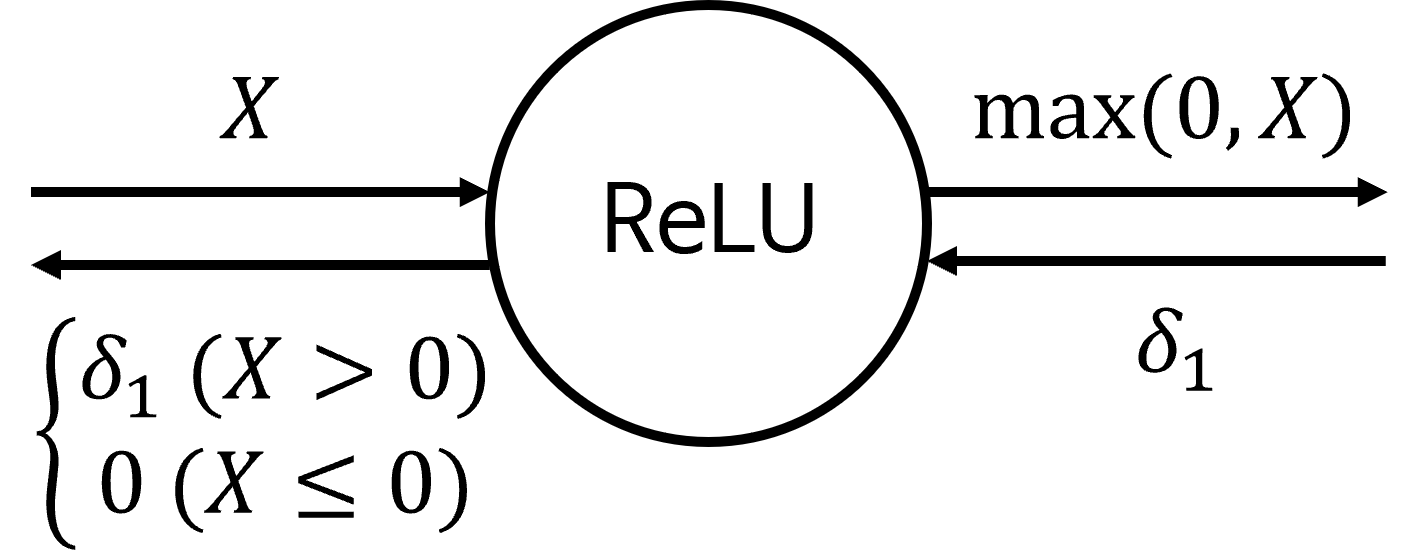
• relu의 식은 max(0, X)와 같이 표현될 수 있습니다. 따라서 relu 층의 입력된 값이 양수이면 gradient도 그대로 전달이되지만 relu층의 입렫된 값이 0 이하의 값이면 0으로 전달됩니다.

transposed convolution

conv1d example

• 지금부터 살펴볼 내용은 numpy를 이용하여 Conv1d를 기준으로 간단한 forward 및 backpropagation 방법에 대하여 알아보도록 하겠습니다.

deep learning 관련 글 목록