Bayesian Neural Network (베이지안 뉴럴 네트워크) 내용 정리

deep learning 관련 글 목차

참조 : https://www.edwith.org/bayesiandeeplearning/

이번 글에서는 베이지안 뉴럴 네트워크에 대한 개념을 정리해 보도록 하겠습니다.

베이지안 뉴럴 네트워크 훑어보기

베이지안 뉴럴 네트워크의 깊은 이론을 살펴보기 전에 베이지안 뉴럴 네트워크의 의미에 대하여 간단하게 알아보도록 하겠습니다.

최신 딥러닝 모델들은 더 큰 모델을 더 많은 데이터로 학습을 진행하고 있습니다. 하지만 모델이 커질수록 해석하기가 어려워지고 해석하기 어려운 딥러닝 모델의 출력값을 얼마나 신뢰할 수 있는 지 알기 어렵습니다.
또한 딥러닝 모델들이 정확한 예측을 하지 못하는 경우가 발생하곤 합니다. 예를들어 학습한 데이터에 노이즈가 있었다거나 학습에 사용하지 않은 데이터가 입력으로 들어오는 경우가 있습니다.
이러한 경우에 단순히 입력을 받으면 출력을 만들어내는 함수와 같은 딥러닝을 믿고 사용할 수 있을 지 의문이 들 수 있습니다. 따라서 딥러닝이 잘 모르는 것을 아는 것이 중요한 문제가 되고 있습니다.

위 사례는 테슬라 자율주행 사고입니다. 트레일러의 사이드를 하늘이라고 판단하여 충돌한 사례입니다. 이와 같은 경우 딥러닝이 정확한 예측을 하지 못하여 인명 피해가 나게 되었습니다. 앞에서 말한 바와 같이 딥러닝이 잘 모르는 상황을 사전에 알 수 있었더라면 이러한 문제를 방지할 수 있었을 것입니다.

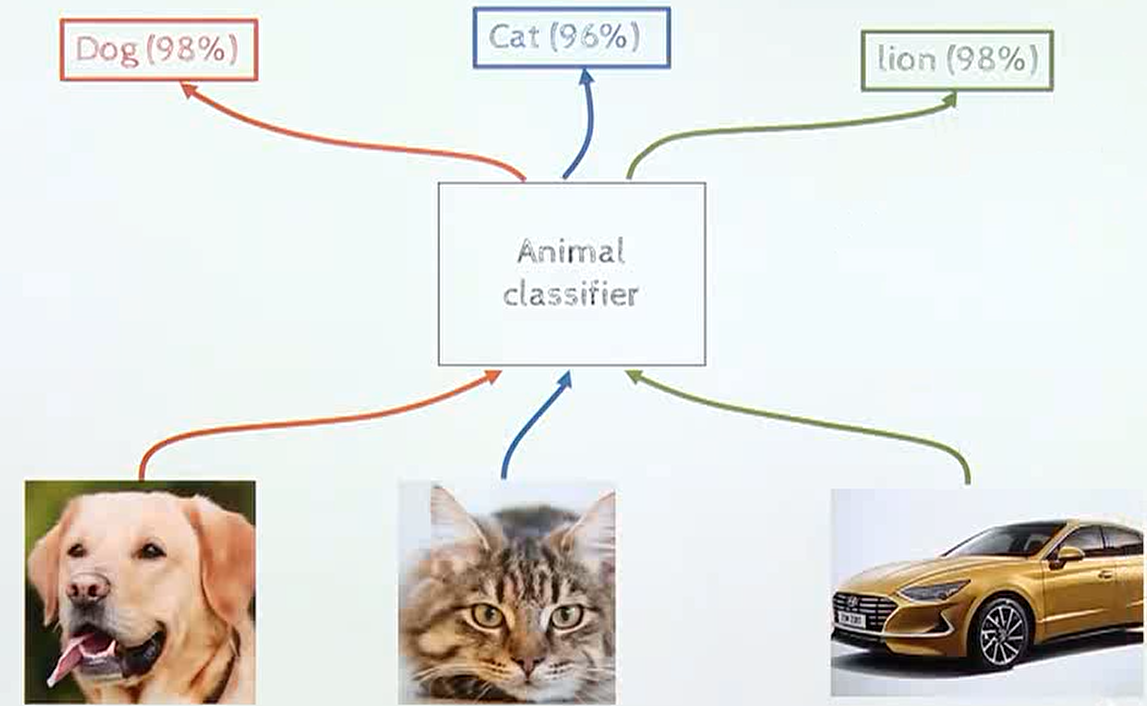
이러한 문제가 발생하는 이유로 딥러닝 기반 인식 시스템의 over-confidence 문제가 있기 때문입니다. 예를 들어 위 그림과 같이 동물 데이터로 학습을 한 뉴럴 네트워크에 자동차를 입력으로 주면 모른다고 출력을 해야 하는데 높은 confidence로 사자라는 답변을 할 수도 있습니다.

이러한 over-confidence 문제가 발생하는 이유로 다양한 원인 분석이 있습니다. 그 중 영향이 큰 원인 중 하나는 학습 데이터 자체가 over-confidence 하도록 만들어 진다는 점입니다. 예를 들어 위 그림과 같이 위 사진을 dog 클래스에 100% 신뢰도로 학습을 시키는 방식을 사용하기 때문에, 학습에 사용하지 않은 자동차라는 데이터가 들어오더라도 over-confidence한 결과를 출력하는 부작용이 발생하게 됩니다.

따라서 딥러닝 시스템을 구축할 때, 딥러닝의 불확실성 (Uncertainty)를 고려할 수 있는 시스템을 만드는 것이 중요합니다.

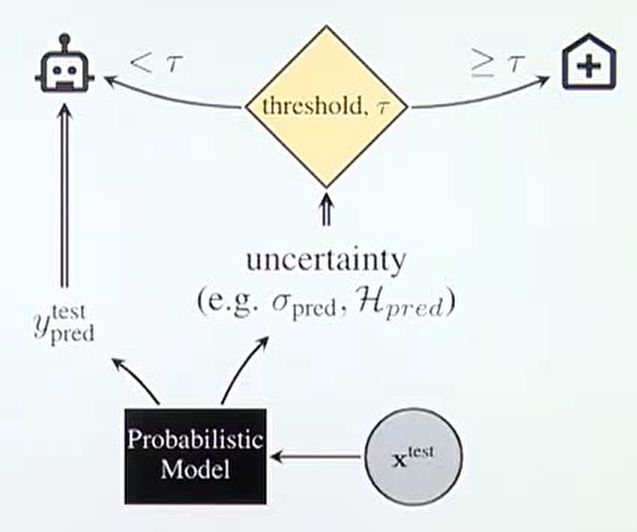
위 Flow와 같이 확률 모델이 입력을 받았을 때, 출력값 \(y\) 와 더불어서 uncertainty도 출력을 하게 됩니다. 이 uncertainty가 특정 threshold인 \(\tau\) 를 넘은 경우 출력값에 대한 별도 검토가 될수 있도록 하면 자율 주행, 의료, 금융 시스템과 같이 불확실성에 매우 민감한 시스템에서의 사고를 예방할 수 있습니다.
이와 같이 확률 모델의 불확실성을 알아야 하는 중요함과 시스템 구축의 필요성을 알아보았습니다. 그러면 어떻게 불확실성을 알 수 있을까요?

머신 러닝에서 불확실성을 다루는 다양한 방법이 있습니다. 그 중 이번 글에서 다룰 내용은 베이지안을 이용하여 불확실성을 구하는 방법에 대하여 다루어 보겠습니다.

먼저 베이지안 방법론에 대한 의미를 다시 한번 리뷰해 보도록 하겠습니다. 베이즈 룰은 기존의 확률 관점인 빈도주의 (frequency)와는 다른 관점을 바라봄으로써 모델이나 현상에 대한 불확실성을 정량화 하려는 시도를 하였습니다. 머신러닝 (딥러닝)에 사용되는 확률 모델의 불확실성을 측정하기 위해서 베이즈 룰을 사용할 수 있고 이러한 방법을 통해 불확실성을 정량화 한 것을 베이지안 머신러닝 (딥러닝) 이라고 합니다.

전통적인 확률 접근론인 빈도주의 관점에서 동전을 던지는 문제를 접근해 보겠습니다. 동전을 무한히 많이 던지면 앞면의 비율은 0.5에 수렴하는 것을 잘 알고 있습니다. 왜냐하면 동전을 무수히 많이 던졌을 때, 앞면이 나온 횟수가 전체의 50%에 수렴하기 때문입니다. 즉, 횟수를 카운팅 하는 빈도주의 접근 방법입니다. 수식으로 쓰면 다음과 같습니다.

\[p(\theta) = \frac{1}{2} \tag{1}\]

만약 동전을 5번 던진 결과 앞면 3번, 뒷면 2번이 관측되었다고 가정해 보겠습니다. 이 때 빈도주의 관점에서 동전의 앞면이 나올 확률이 얼마일까요?
빈도주의 관점에서도 무한히 많이 던져 봐야 결과를 알 수 있다고 말할 수 있지만, 현재 상황에서는 \(p(\theta) = \frac{3}{5}\) 이라고 결론을 냅니다.

반면 베이지안 관점에서는 확률 자체를 불확실성으로 바라봅니다.

\[p(\theta) = \frac{1}{2}\]

위 식에 대하여 빈도주의는 동전의 앞면이 나올 확률이 50 % 라고 단정짓지만 베이지안에서는 동전의 앞면이 나올 가능성이 50 % 정도이라 라고 결론을 내립니다. 즉, 불확실성을 내포하고 있습니다.
따라서 베이지안에서는 빈도주의와 같이 확률 모델을 계속 학습하여 고정된 참 값의 확률을 찾아가는 것이 아니라 아래와 같이 불확실성을 내포한 확률 분포를 찾는 것이 목적이 됩니다.

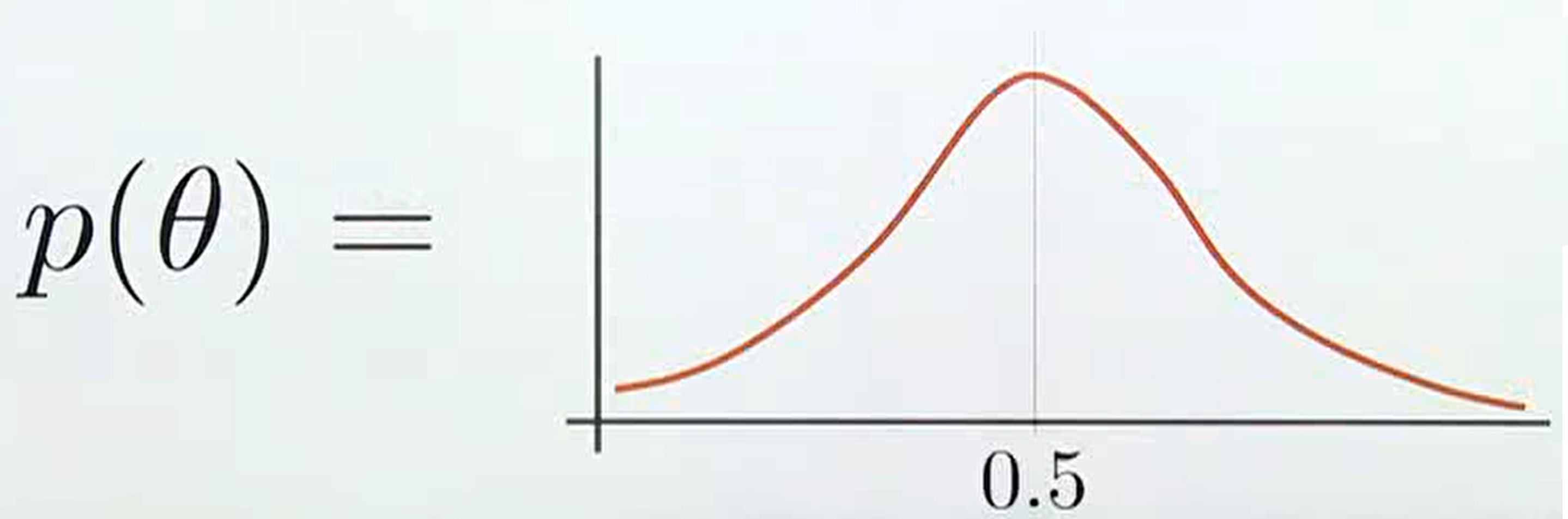
빈도주의에서는 확률값이 고정되기 때문에 어떤 확률값에 variance가 없이 고정이 되지만 베이지안에서는 정해진 확률값이 없이 분포로 나타나고 이 분포에는 variance가 존재하므로 불확실성을 내포하게 됩니다. 간단히 정리하면 불확실성의 정량화는 variance를 통해 나타나집니다.
흔히 알고 있듯이 동전의 앞면이 나온 확률이 0.5 라는 사전 지식으로 위 그래프와 같이 앞면이 나올 확률이 0.5에서 가장 높은 likelihood를 가지게 되지만 (prior distribution) 앞의 예제와 같이 앞면이 3번 뒷면이 2번 나오게 되면 확률 분포의 가장 큰 likelihood가 0.5 보다 더 큰 쪽으로 옮겨지게 되도록 업데이트 됩니다.. (posterior distribution) 수식으로 표현하면 아래와 같습니다.

\[D = (\text{F, T, T, F, F, F}) \tag{2}\]
\[p(\theta) = \frac{1}{2} \tag{3}\]
\[p(\theta \vert D) \gt p(\theta) = \frac{1}{2} \tag{4}\]

빈도주의와 베이지안의 관점 차이를 정리하면 위 그림과 같습니다. 베이지안의 핵심은 불확실성을 나타내는 확률 분포가 업데이트 된다는 것입니다.
이 때, 식 (4)와 같이 데이터 \(D\) 를 관찰한 후에 모델의 불확실성을 표현하는 확률 분포를 posterior distribution 이라고 합니다.

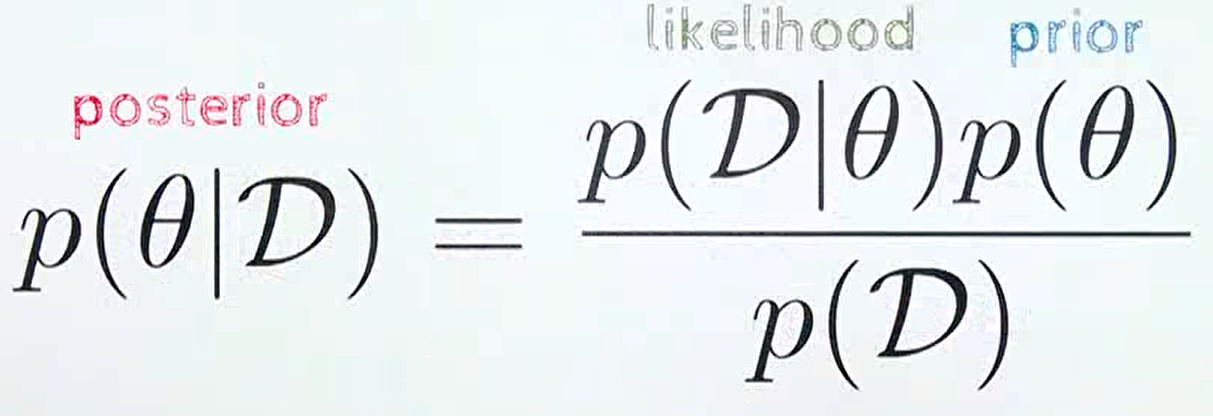
위 식은 흔히 잘 알고있는 베이즈 룰을 나타낸 식입니다.
prior는 새로운 데이터 \(D\) 를 관찰하기 전에 알고 있는 사전 분포에 해당합니다. 앞에서 상식적으로 알고 있는 앞면이 나올 확률 0.5가 이에 해당합니다.
likelihood는 현재 확률 모델이 얼마나 데이터를 잘 설명하는 지 나타내는 정량화된 값입니다. 이 값은 빈도주의에서 살펴본 확률 표현 방법과 같으며 3/5에 해당합니다.
posterior는 likelihood 값을 이용하여 prior → posterior로 업데이트 하는 것으로 이해할 수 있습니다.

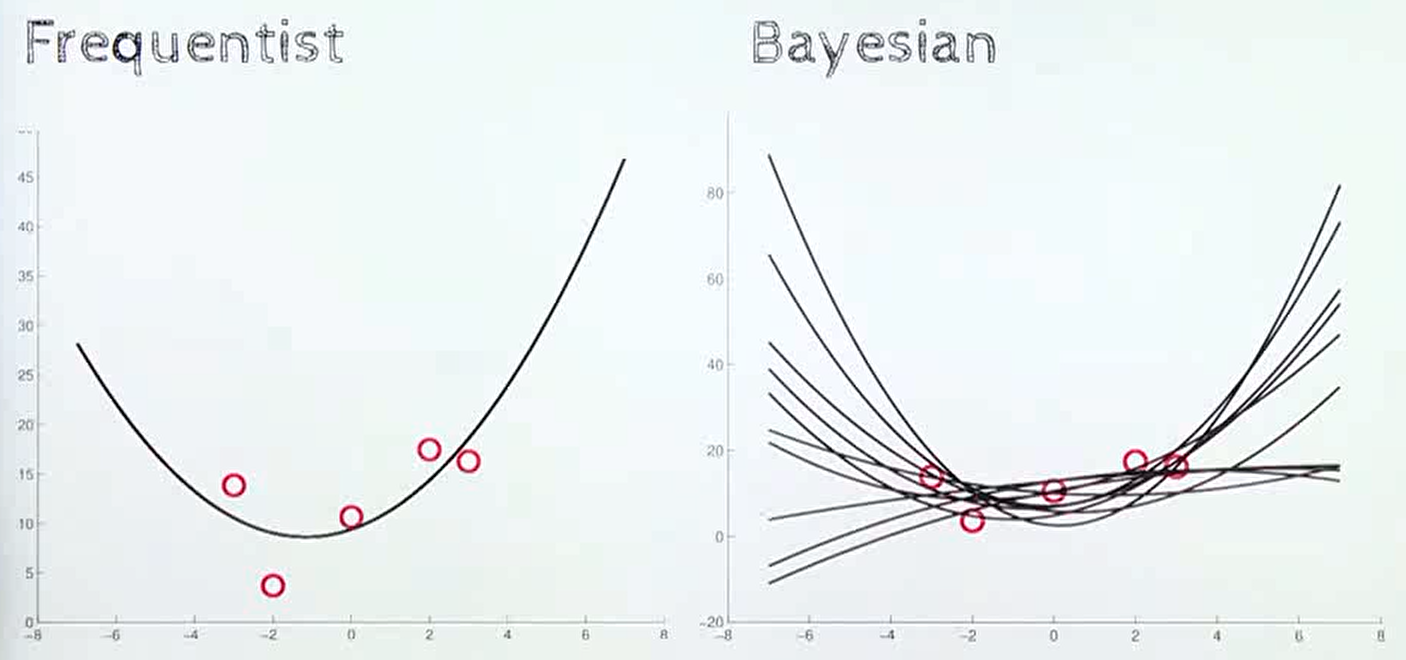
빈도주의 방법과 베이지안 방법의 차이는 다양한 분야에서 관찰할 수 있습니다. 위 그림과 같은 regression 문제에서도 확인할 수 있습니다.
빈도주의의 경우 주어진 데이터를 가장 잘 설명할 수 있는 곡선을 하나 추정하는 것을 목표로 하지만 베이지안에서는 예측 자체가 불확실한 값이기 때문에 여러가지 가능한 함수가 있다고 이해하게 됩니다.

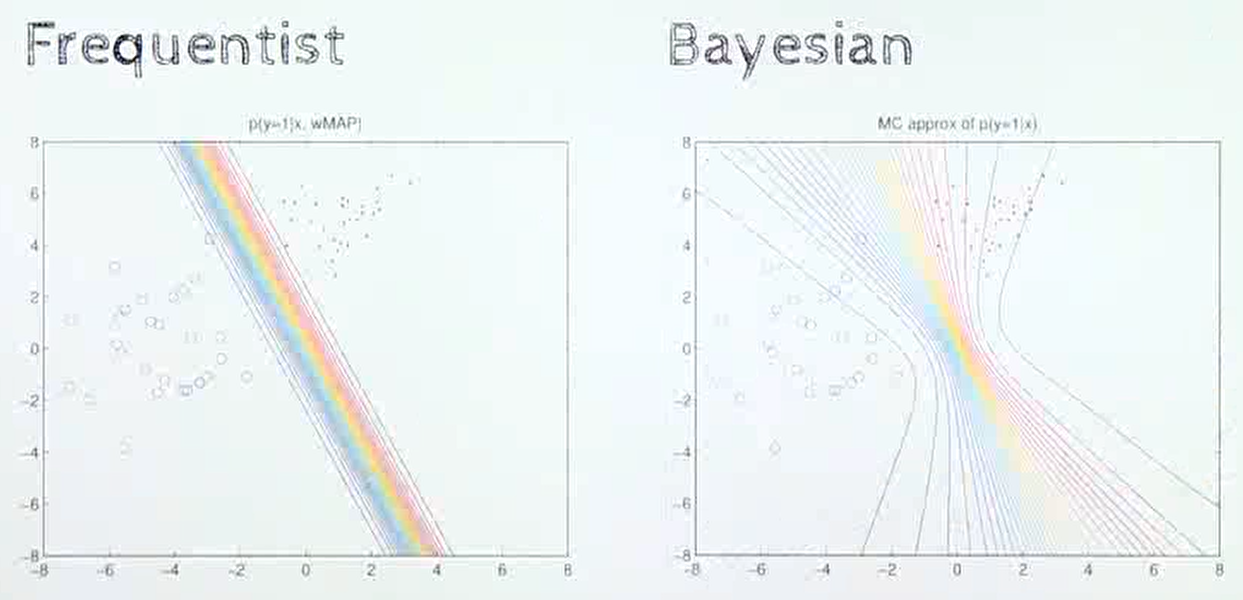
분류 문제를 풀 때에도 빈도주의는 클래스를 분류하는 고정된 선을 이용하지만 베이지안에서는 입력된 데이터에 따라 다양한 형태의 곡선을 나타냅니다.

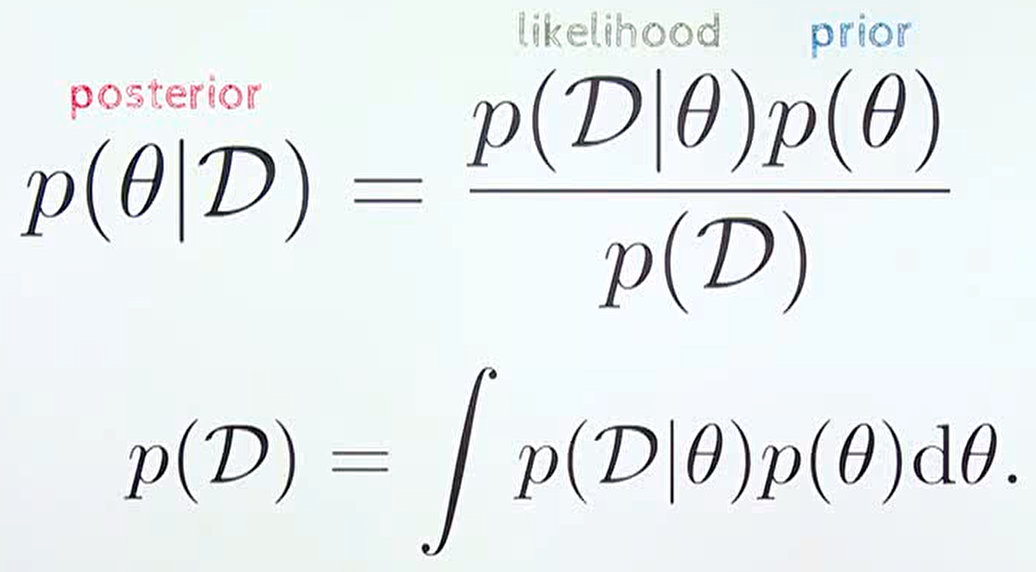
지금까지 살펴본 바와 같이 베이지안 방법론은 불확실성을 정량화 할 수 있는 수단이라는 장점을 가지지만 posterior를 계산하기 위한 \(p(D)\) 의 적분 계산이 불가능한 경우가 다수 발생합니다.
기존의 머신러닝 방법에서는 한정된 파라미터의 갯수로 인하여 적분식을 그대로 계산하지 못하더라도 적분식의 결과를 근사화 하는 기법이 사용되었지만, 딥러닝과 같이 기하급수적으로 많은 파라미터를 대상으로 적분 또는 근사화 하는 것에 어려움이 있어 베이지안 뉴럴 네트워크라는 개념이 도입 되었습니다.

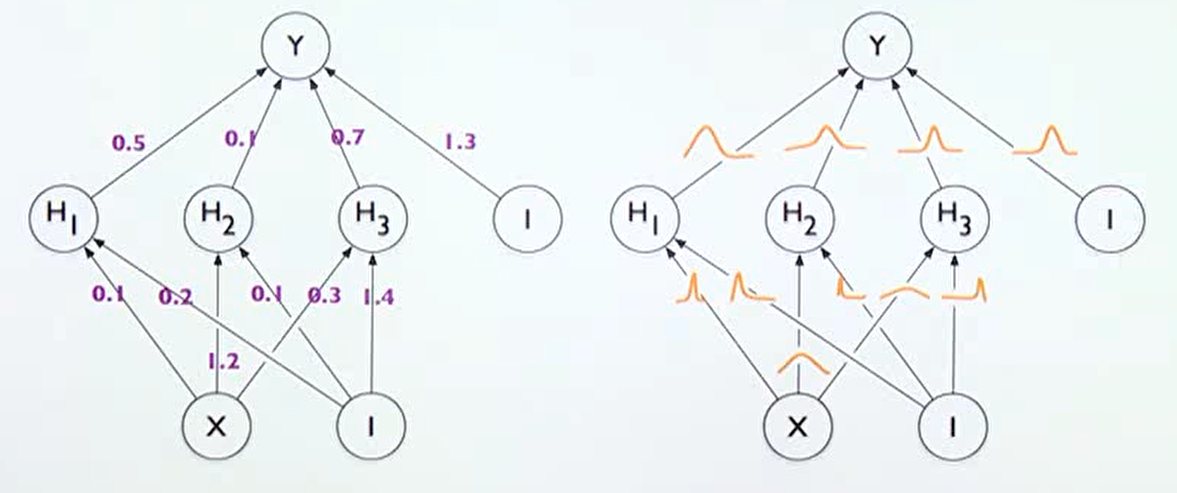
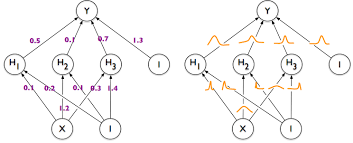
베이지안 뉴럴 네트워크는 위 오른쪽 그림과 같이 표현될 수 있습니다.
기존의 뉴럴 네트워크는 학습이 끝나면 weight가 고정된 값을 가지게 되지만 베이지안 뉴럴 네트워크는 각 weight 또한 불확실성을 가지는 확률 분포로 나타나 진다는 점에서 차이가 있습니다. 각 weight가 불확실성을 가지는 확률 분포이므로 최종 출력인 \(Y\) 또한 불확실성을 가지는 확률 분포를 가지게 됩니다.

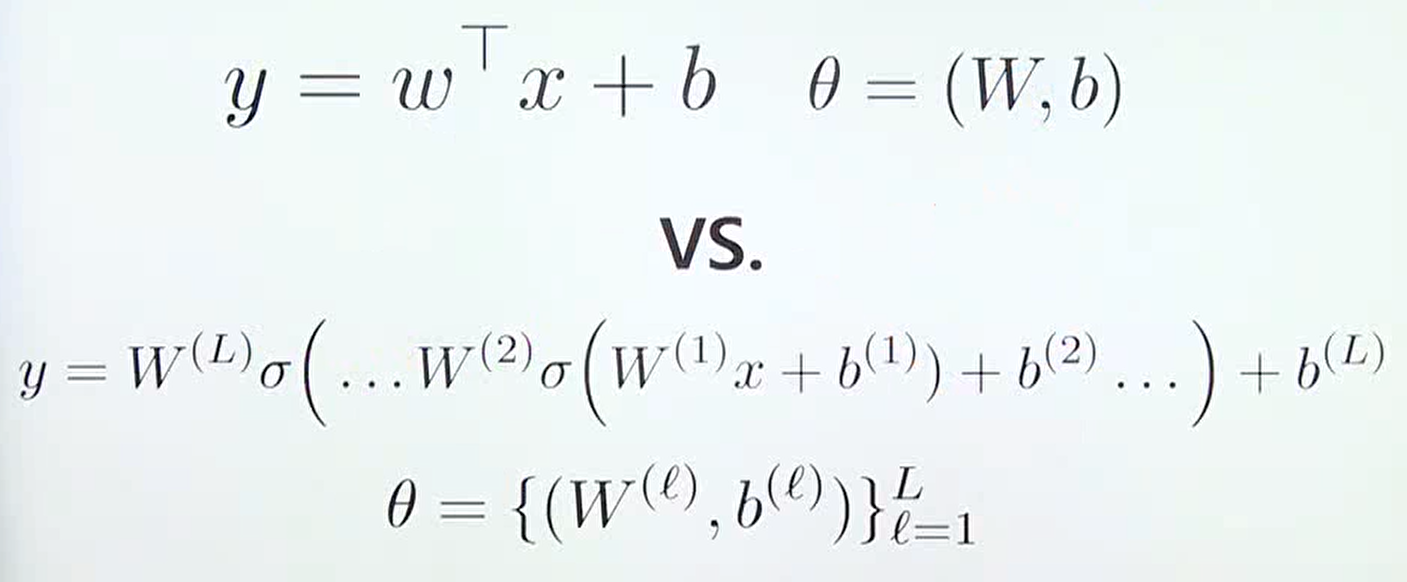
위 식을 살펴보면 기본적인 선형 모델과 뉴럴 네트워크가 복잡도에는 차이가 있지만 근본적인 컨셉은 같다는 것을 표현합니다.
베이지안 뉴럴 네트워크의 관점에서는 모든 \(\theta\) 값인 모든 \(W, b\) 에 대하여 prior distribution을 가지고 어떻게 posterior distribution으로 업데이트 할 것인 지를 다룬다고 말할 수 있습니다.

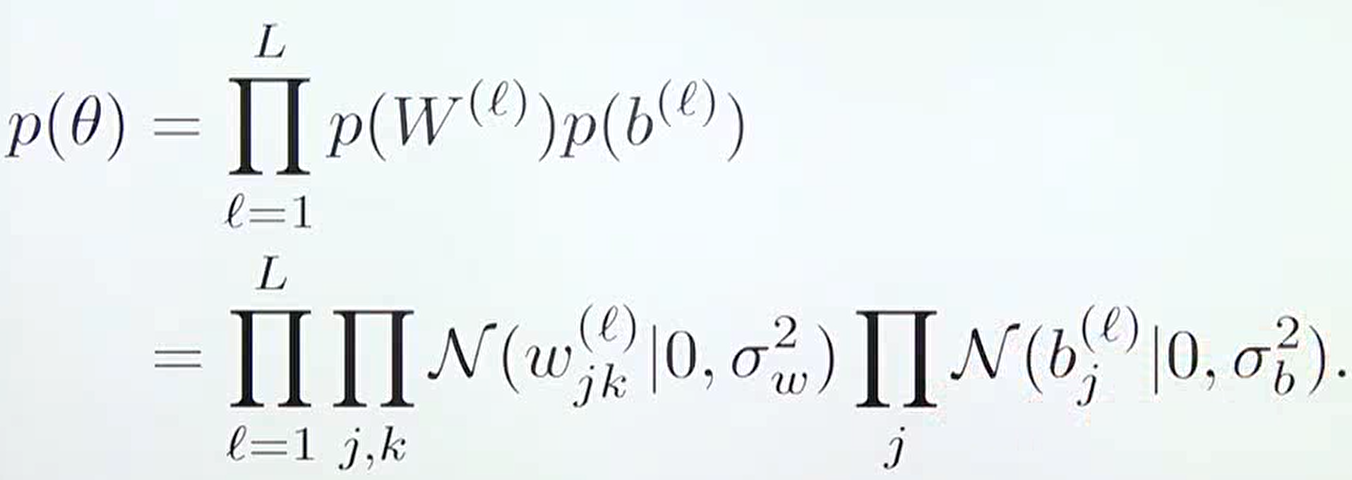
보통 딥러닝에서 사용하는 사전 확률 분포는 정규 분포 (가우시안 분포)를 따른다고 가정하며 위 식과 같은 형태를 가집니다. 흔히 사용하는 Xavier, He initialization 또한 정규 분포 형태를 가지므로 위 식과 유사한 형태를 가지게 됩니다.

따라서 베이지안 뉴럴 네트워크의 베이지안 추론은 다음과 같이 파라미터의 posterior distribution을 계산합니다.

\[p(\theta \vert X, y) = \frac{p(y \vert X,\theta)p(\theta)}{p(y \vert X)}\]

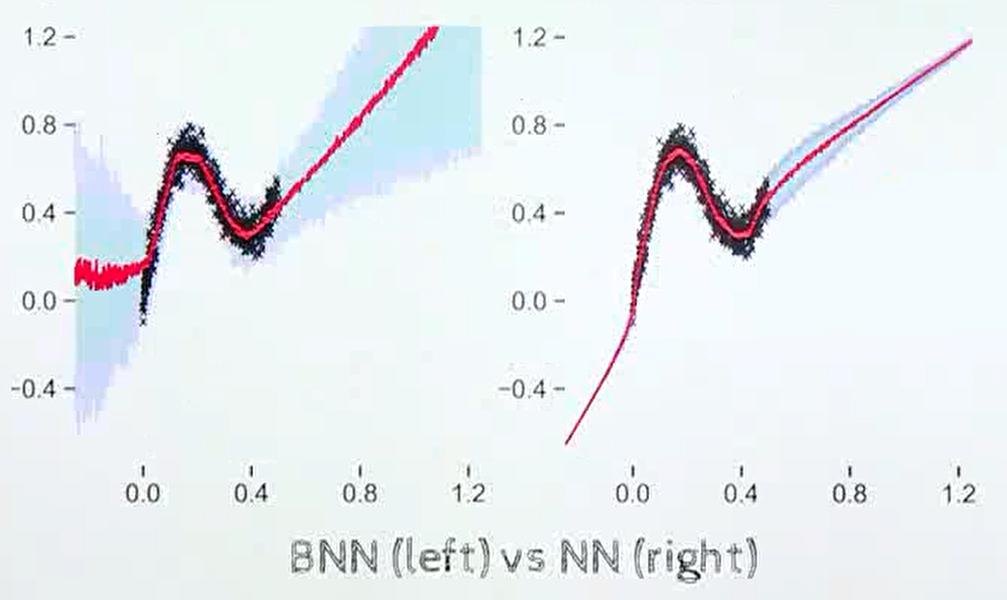
두 뉴럴 네트워크를 비교해서 보면 왼쪽은 베이지안 뉴럴 네트워크이고 오른쪽은 일반적인 뉴럴 네트워크 입니다.
검은색 점이 실제 학습 데이터가 입력된 구간에 해당하며 빨간색 선은 뉴럴 네트워크의 출력에 해당합니다. 빨간색 선 주위의 음영은 불확실성을 나타내게 됩니다.
베이지안 뉴럴 네트워크의 경우 데이터가 없는 구간의 경우 불확실성이 크게 나타나지만 뉴럴 네트워크의 경우 학습 데이터가 없는 구간에도 불확실성이 낮다는 점을 확인할 수 있습니다.

하지만 앞에서 계속 언급한 바와 같이 posterior distribution을 정확하게 계산할 수 없다는 문제가 남아 있습니다.
이 문제를 해결하기 위하여 다양한 방법이 있으며 대표적으로는 variational inference 방법을 사용하는 것과 Monte Carlo Dropout을 사용하는 방법이 있습니다.

variational inference는 posterior distribution인 \(p(\theta \vert D)\) 를 \(p(\theta \vert D) \approx q(\theta)\) 와 같은 방법으로 근사화 하는 방법을 의미합니다. 이 때, \(q(\theta)\) 는 접근하기 쉬운 정규 분포와 같은 확률 분포를 사용합니다. 자세한 내용은 아래 링크를 참조해 주시기 바랍니다.
- 링크 : https://gaussian37.github.io/ml-concept-variational_inference/
variational inference를 사용하면 완벽한 근사화는 아니지만 원래 posterior distribution이 가지는 특징을 잘 캡쳐할 수 있도록 근사화 할 수 있습니다.

그 다음으로 MC (Monte Carlo) dropout 방법이 있습니다.
dropout은 뉴럴 네트워크에서 Feedforward할 때, 임시로 뉴런의 관계를 확률적으로 끊어서 딥러닝의 Regularization 효과를 주기 위한 기법입니다.

위 영상을 참조하면 dropout 적용 시 어떤 동작을 하는 지 살펴볼 수 있습니다. 추가적으로 오른쪽의 초록색 선으로 불확실성을 표현하였는데 학습 데이터가 부족한 부분에서 불확실성이 큰 것을 볼 수 있습니다.
일반적으로 dropout은 학습 시 특정 weight에 값이 치중되어 overfitting되는 문제를 개선하기 위한 regularization 방법으로 많이 사용되고 테스트 시에는 일관적인 출력을 만들어 내기 위하여 의도적으로 dropout을 배제합니다.
Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning 반면 Yarin Gal의 논문에서는 테스트 시 Dropout을 그대로 사용하여 여러번의 출력값을 만들어내고 이 출력 값들을 이용하여 평균을 구하면 posterior distribution에 근사화 할 수 있음을 유도하였습니다.

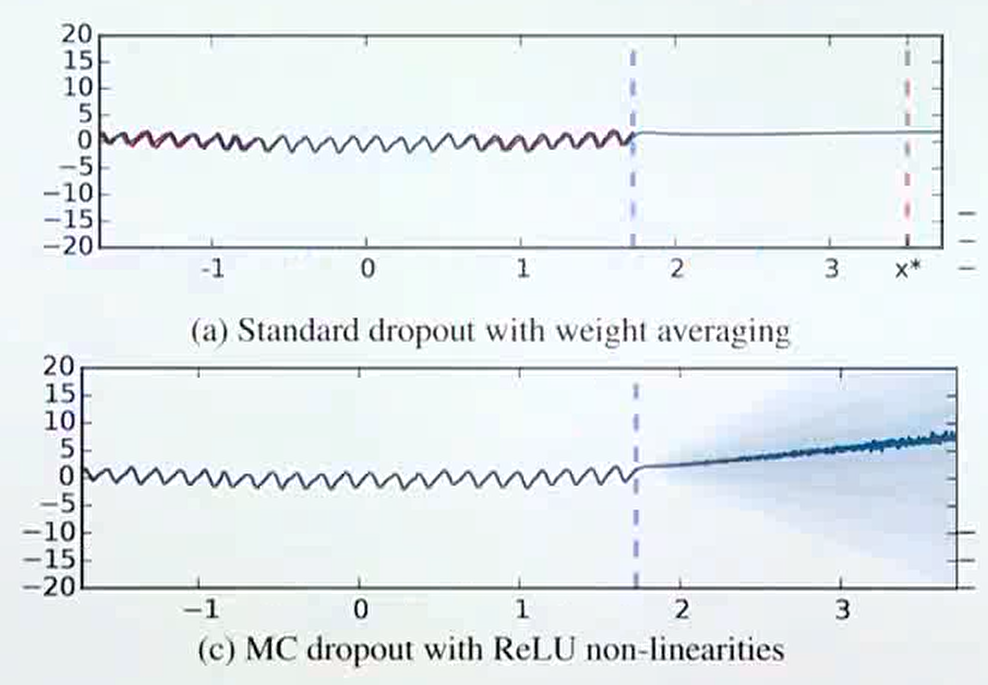
위 그림은 regression과 관련된 문제에서의 MC dropout의 효과를 나타냅니다. 파란색 점선이 있는 곳까지가 실제 데이터로 학습이 된 구간이며 파란색 점선 이후에는 학습된 적이 없는 데이터 입니다.
(a)는 고정된 dropout 하나를 사용하여 출력을 낸 결과 학습하지 않은 영역에서의 출력도 일관성 있게 나오는 것을 알 수 있습니다.
(c)는 여러개의 dropout을 사용하여 나온 출력을 통해 확률 분포를 구하고 이 결과를 통해 학습하지 않은 구간의 출력을 살펴본 경우입니다. (c) 그림의 파란색 음영과 같이 불확실성이 매 우 큰 것을 확인할 수 있습니다.

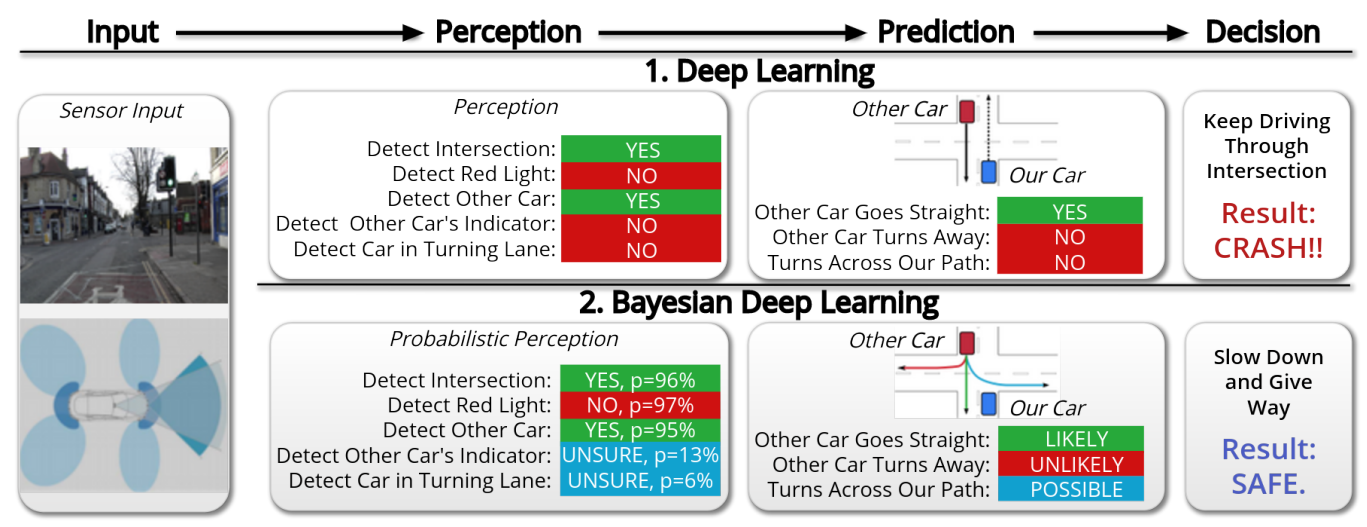
관련 논문 : Concrete Problems for Autonomous Vehicle Safety: Advantages of Bayesian Deep Learning
위 Yarin Gal의 논문은 자율주행에서의 베이지안 딥러닝의 어플리케이션에 관한 내용입니다.
위 표와 같이 베이지안 딥러닝 시스템을 사용하면 불확실성을 모델링 할 수 있고 기존에는 Turns Across Our Path = NO 라고 판단한 부분이 POSSIBLE로 바뀌게 됨으로써 좀 더 안전한 시스템을 구축할 수 있게 됩니다. 이와 같이 불확실성이 높은 경우 제어권을 운전자에게 줄 수 있도록 판단이 가능해집니다.

대표적인 픽셀 기반 컴퓨터 비전 어플리케이션인 시멘틱 세그멘테이션과 뎁스 추정 문제에서의 불확실성을 살펴보면 객체의 경계 부분 또는 예측이 어려운 부분에서의 불확실성이 높게 나타나는 것을 볼 수 있습니다. (Uncertainty에서 color 파란색 이외의 색, 빨간색에 가까울수록 불확실성이 높다고 판단할 수 있음)

불확실성을 이용할 수 있는 또 다른 분야에는 active learning이 있습니다.
관련 논문 : Deep Bayesian Active Learning with Image Data

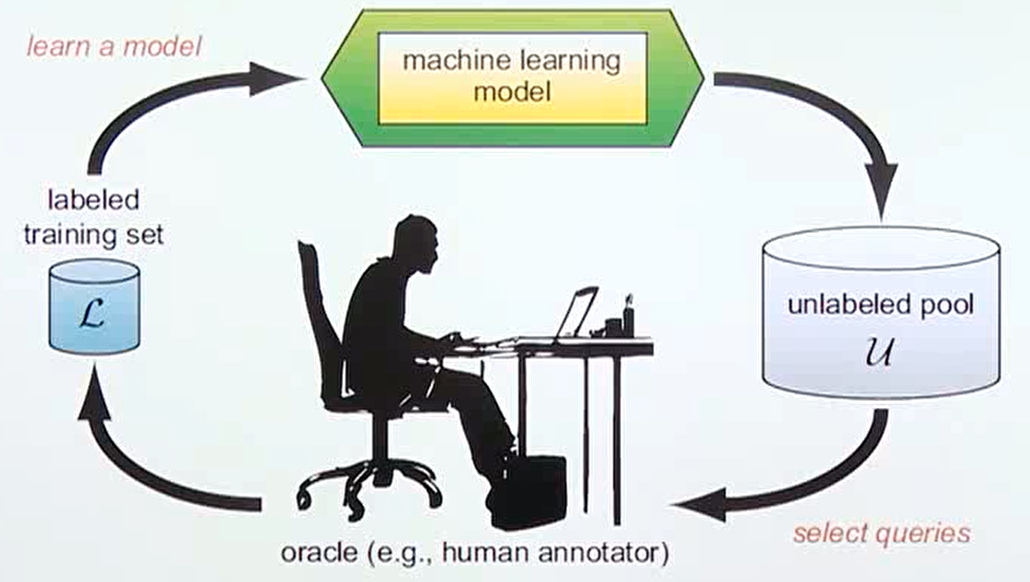
active learning은 라벨링 되어 있는 데이터를 이용하여 아직 라벨링 되지 않은 데이터 중 어떤 데이터를 라벨링 해야 성능 향상에 효과적인 지 판단하는 문제입니다. 즉, 비용 절감을 위하여 라벨링 해야 할 이미지를 최소화 하고 효과는 최대화 하는 전략이라고 말할 수 있습니다.

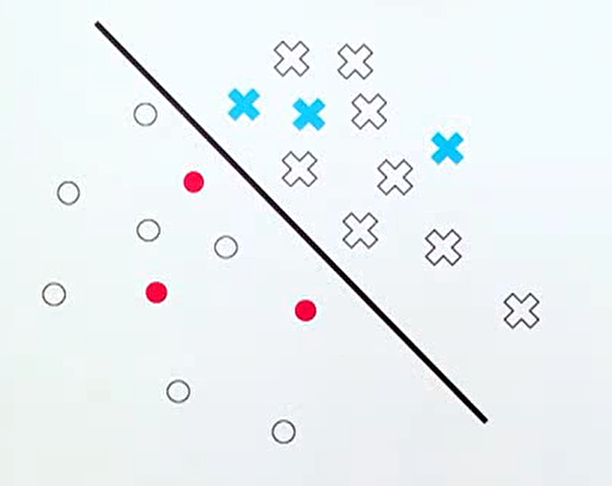
직관적으로 위 그림과 같은 classification 문제에서 빨간색과 파란색 데이터는 라벨링이 되어서 학습에 사용된 데이터이고 흰색 데이터가 아직 라벨링 되지 않은 데이터라고 하면 어떤 흰색 데이터 부터 먼저 라벨링 하는 것이 효과적일까요? 정답은 classifier인 선에 가까운 데이터 부터 라벨링 해야 불확실성이 감소됩니다.
따라서 베이지안 뉴럴 네트워크를 이용하여 불확실성을 측정하고 불확실성이 큰 데이터 위주로 먼저 라벨링 하면 효과적인 active learning을 할 수 있습니다.

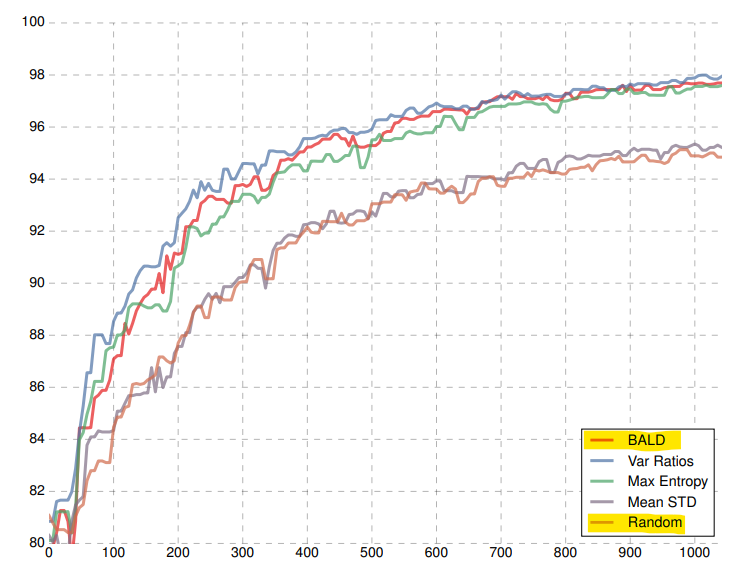
이러한 방법으로 active learning을 실시한 결과 단순히 랜덤으로 선택하여 추가 학습을 한 것 보다 훨씬 더 빨리 성능 향상을 할 수 있는 것을 알 수 있습니다.

deep learning 관련 글 목차