Convolution 연산 정리 (w/ Pytorch)

2019, Nov 05    

• 출처 : https://towardsdatascience.com/conv2d-to-finally-understand-what-happens-in-the-forward-pass-1bbaafb0b148
• 출처 : https://github.com/vdumoulin/conv_arithmetic
• 출처 : https://pytorch.org/docs/master/generated/torch.nn.Conv2d.html

목차

• Convolution 연산 소개

• Kernel 이란

• Trainable parameter와 bias 란

• Input, output channel의 갯수란

• Kernel의 size 란

• Stride 란

• Padding 이란

• Dilation 이란

• Group 이란

• Output Channel Size 란

• Basic Convolution Operation

• Pytorch Convolution Operation

Convolution 연산 소개

• 이번 글에서는 영상 처리를 위한 딥러닝을 사용할 때 기본적으로 사용되는 convolution 연산에 대하여 다루어 보려고 합니다.
• convolution 연산은 예를 들면 아래 그림과 같습니다.

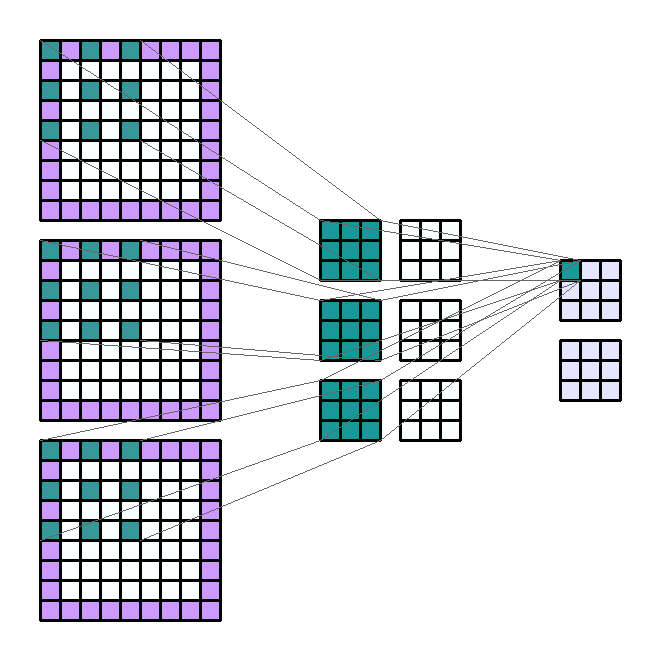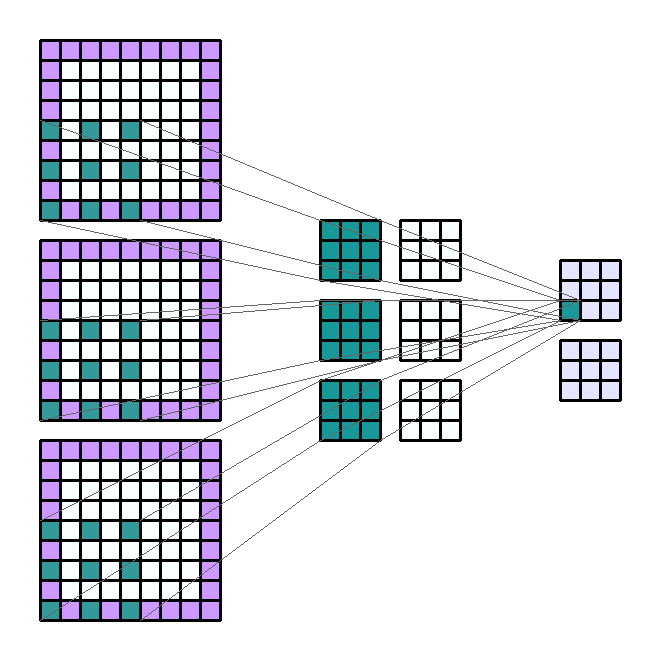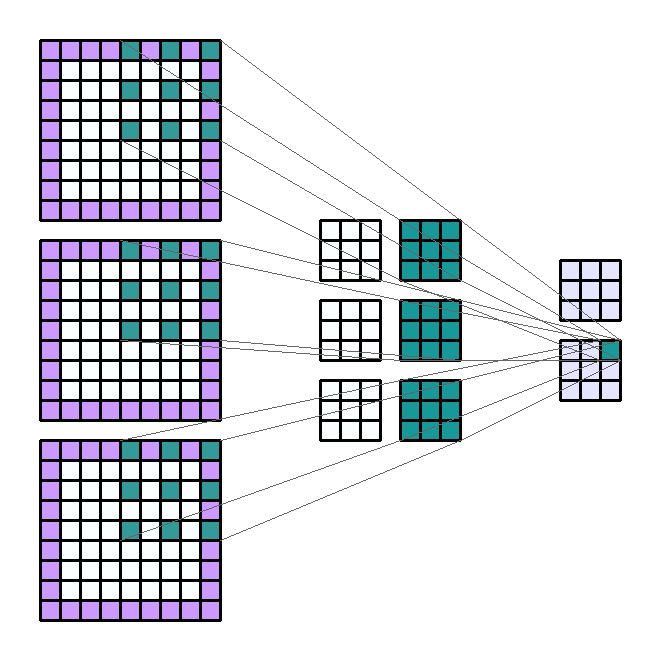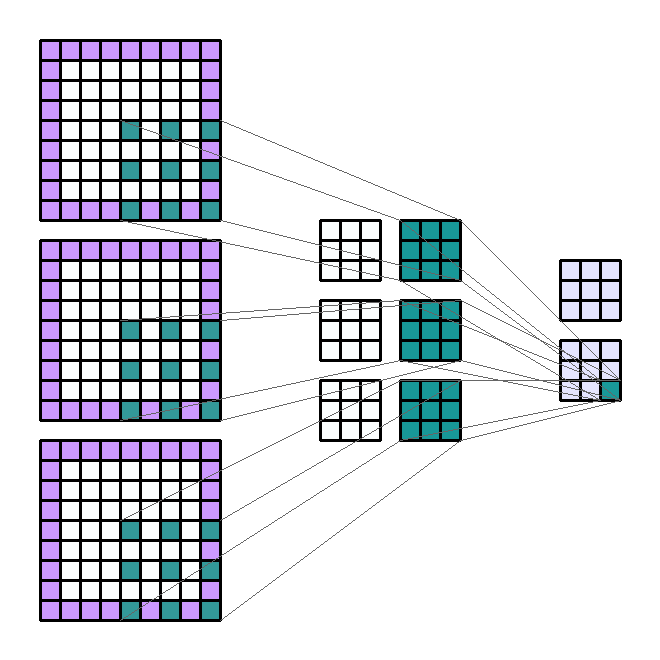
• 영상 처리의 입력에 사용되는 영상은 일반적으로 3차원의 형태를 가집니다. 즉, 영상의 width, height, channel 3가지가 기본 요소이며 Framework에 따라 (channel, height, width)의 순서 또는 (height, width, channel) 순서로 영상을 표시합니다. 이번 글에는 (height, width, channel)의 순서로 영상을 표시해 보도록 하겠습니다. channel은 예를 들어 R,G,B 값이 될 수 있습니다.
• 그러면 위 이미지의 가장 왼쪽이 Input 일 때, (7, 7, 3)의 크기를 가집니다. 그리고 Output은 (3, 3, 2)의 크기를 가집니다. 연산의 속성들을 정리하면 다음과 같습니다.

• Input shape : (7, 7, 3)
• Output shape : (3, 3, 2)
• Kernel shape : (3, 3)
• Stride : (2, 2)
• Padding : (1, 1)
• Dilation : (2, 2)
• Group : 1

• Input, output을 제외한 Kernel, Padding, Dilation, Group은 Convolution 영상 기법에 해당합니다. 이 내용에 대하여 간략하게 알아보도록 하겠습니다.
• 먼저 Pytorch의 Conv2d 모듈의 파라미터들을 살펴보겠습니다. 위의 convolution 연산과 동일한 파라미터가 필요합니다.

• in_channels (int) — Number of channels in the input image
• out_channels (int) — Number of channels produced by the convolution
• kernel_size (int or tuple) — Size of the convolving kernel
• stride (int or tuple, optional) — Stride of the convolution. Default: 1
• padding (int or tuple, optional) — Zero-padding added to both sides of the input. Default: 0
• dilation (int or tuple, optional) — Spacing between kernel elements. Default: 1
• groups (int, optional) — Number of blocked connections from input channels to output channels. Default: 1
• bias (bool, optional) — If True, adds a learnable bias to the output. Default: True

• 그러면 위 키워드 들을 하나 하나 다루어 보도록 하겠습니다.

Kernel 이란

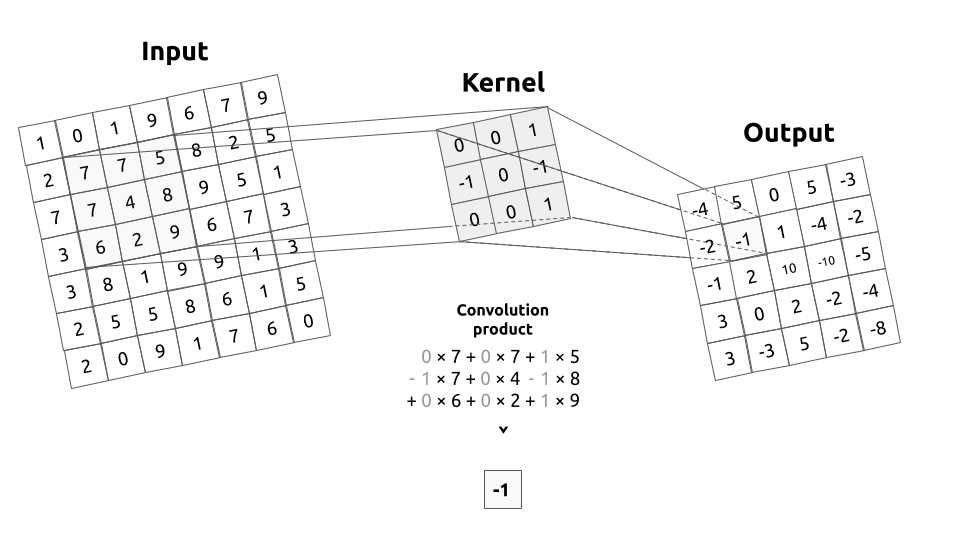
• kernel 또는 filter라고 하는 convolution matrix는 input image의 전 영역들에 걸쳐서 연산 됩니다.
• 일반적으로 left-top → right-bottom 방향으로 sliding window를 하면서 연산이 됩니다. 이 때 각 영역에서 convolution product가 연산됩니다. 이 연산을 거치기 전을 Input image 이라고 한다면 연산 후는 filtered image 라고 합니다.
• 위 그림에서 convolution product를 살펴보면 kernel의 각 원소와 1 대 1 대응이 되는 Input 영역이 있고 Input의 값과 kernel의 값을 곱한 뒤 그 결과를 모두 더하면 output 픽셀 하나가 완성됨을 볼 수 있습니다. 즉, element-wise multiplication 연산을 합니다.
• 그러면 이 연산을 수식으로 표현해 보겠습니다.

• \[G(x, y) = w * F(x, y) = \sum_{\delta x = -k_{i}}^{k_{i}} \sum_{\delta y = -k_{j}}^{k_{j}} w(\delta x, \delta y) \cdot F(x + \delta x, y + \delta y)\]
• \[w \text{ is kernel and } -k_{i} \ge \delta x \ge k_{i}, \ \ -k_{j} \ge \delta y \ge k_{j}\]

• 위 수식에서 \(\delta x, \delta y\) 각각은 현재 convolution product가 되는 kernel의 중앙 위치가 이미지 좌표계 원점에서 얼만큼 떨어져 있는지를 나타냅니다.

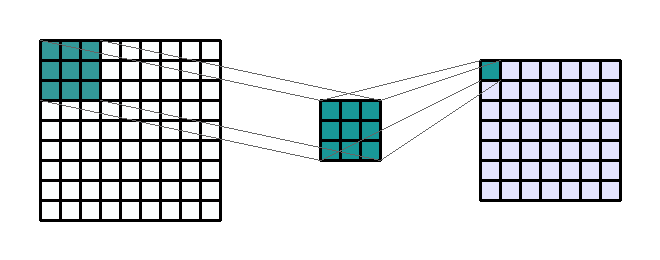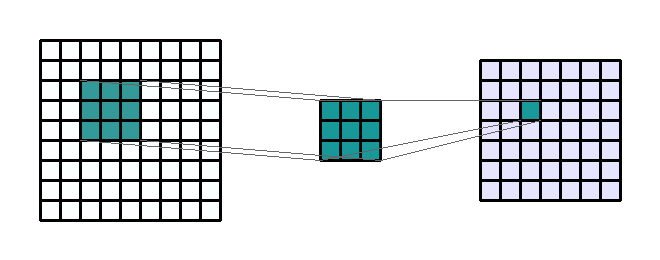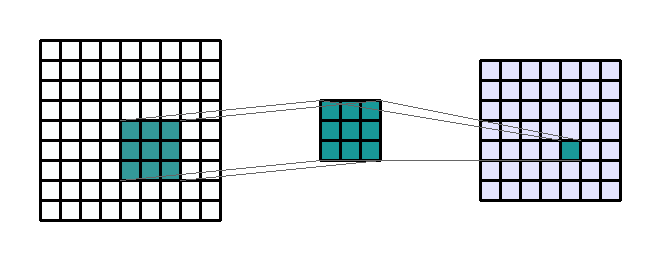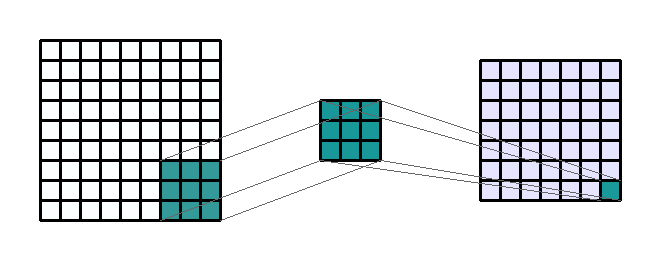
• 연산의 과정을 위 예제를 통해 정리해 보겠습니다. 위 예제에서는 Input image의 크기는 (9, 9, 1) 입니다. kernel의 크기는 (3, 3) 입니다. kernel은 Input image의 전 영역을 sliding window 하면서 element-wise multiplication 연산을 하게 되고 각 연산은 (1, 1)의 scalar 값을 가지게 됩니다.

Trainable parameter와 bias 란

• parameter들은 학습 과정 동안 update 됩니다. Conv2d에서 학습이 되는 parameter는 무엇일까요? 바로 kernel 입니다.
• 앞의 예제에서 (3, 3) 크기의 kernel을 이용하여 convolution 연산을 하였습니다. 이 때 사용된 9 개의 원소가 학습할 때 업데이트가 되는 parameter 입니다.

• \[w * F(x, y) = \Biggl( \sum_{\delta x = -k_{i}}^{k_{i}} \sum_{\delta y = -k_{j}}^{k_{j}} w(\delta x, \delta y) \cdot F(x + \delta x, y + \delta y) \Biggr) + w_{bias}\]
• \[\text{where } w_{bias} \in \mathbb R \text{ is the bias of the kernel } w\]

• 만약 bias 까지 포함하여 생각한다면 위 수식처럼 표현할 수 있습니다. bias는 convolution product 연산한 값에 덧셈을 해주는 trainable parameter 입니다.
• 만약 앞에서 다룬 예제에서 (3, 3) kernel에 bias가 추가된다면 parameter의 갯수는 총 몇개가 될까요? 9 + 1 = 10개가 됩니다.

Input, output channel의 갯수란

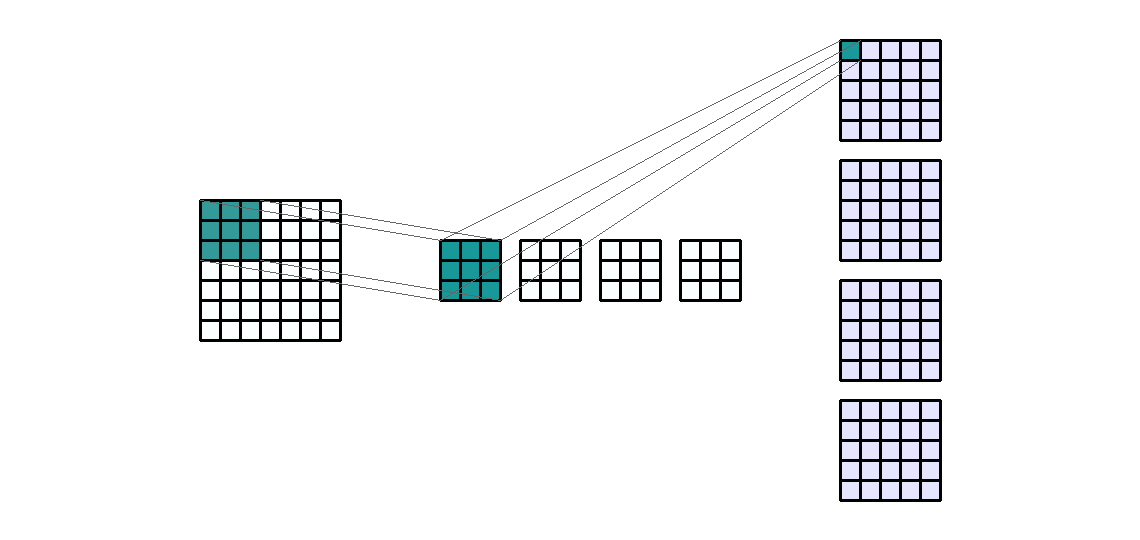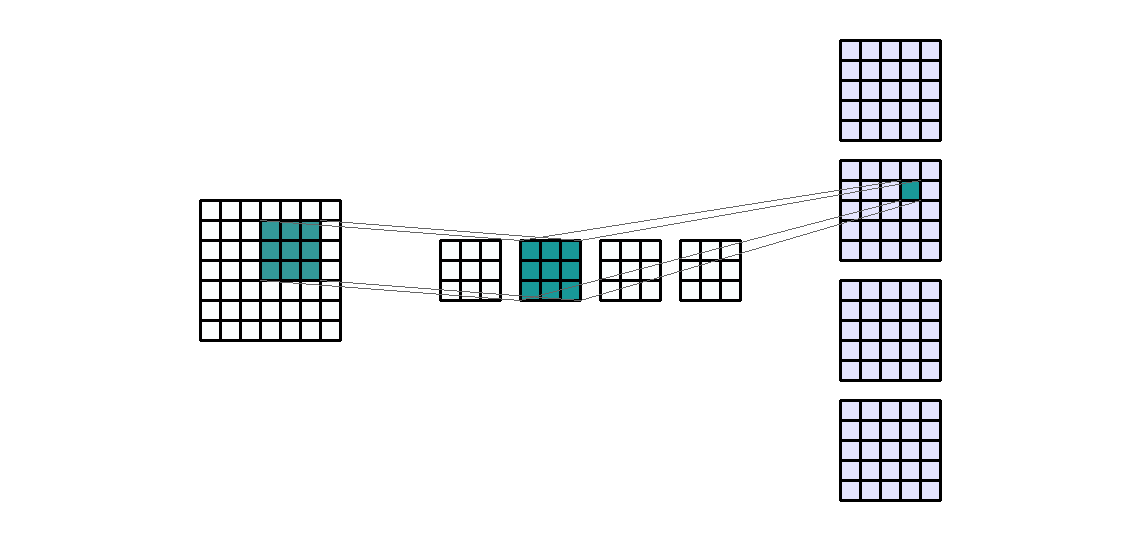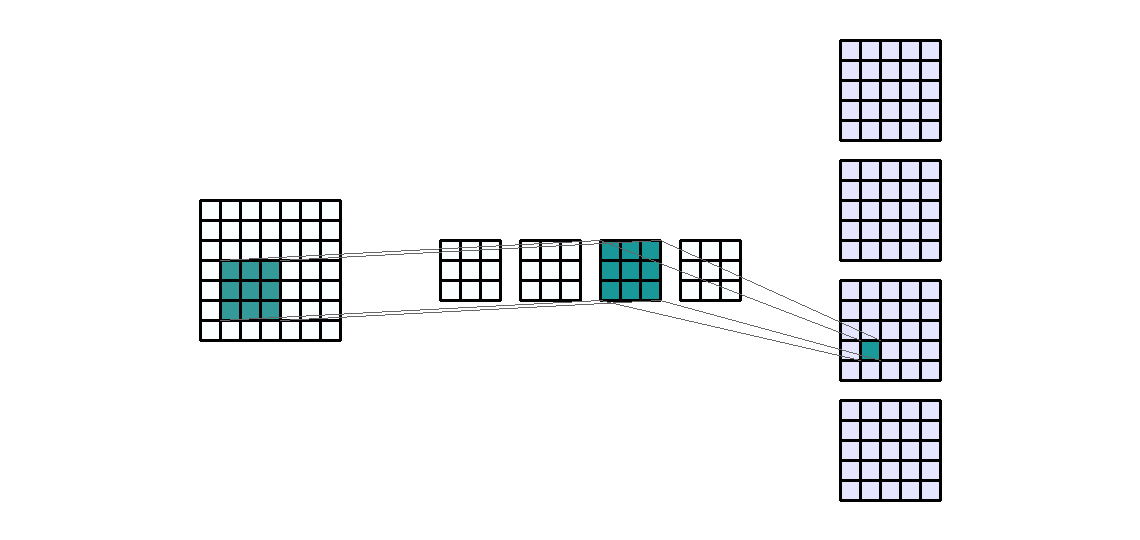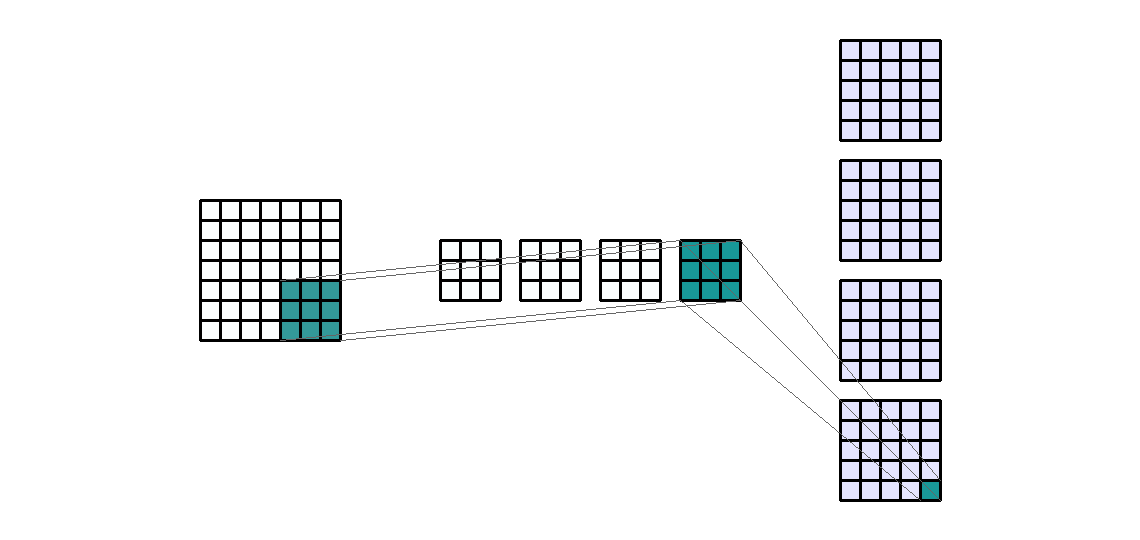
• 위 예제의 속성을 먼저 살펴보면 다음과 같습니다.

• Input shape : (7, 7, 1)
• Output shape : (5, 5, 4)
• Kernel shape : (3, 3)
• Stride : (1, 1)
• Padding : (0, 0)
• Dilation : (1, 1)
• Group : 1

• convolution 연산을 할 때, layer를 만드는 이유는 유사한 convolution 연산을 한번에 하기 위해서 입니다.
• 예를 들어 위 그림과 같이 kernel의 갯수가 4개 있다고 하면, 각 kernel은 동일한 연산을 하여 4개의 output을 만듭니다.

• \[G_{out}(x, y) = w_{out} * F(x, y) = \Biggl( \sum_{\delta x = -k_{i}}^{k_{i}} \sum_{\delta y = -k_{j}}^{k_{j}} w_{out}(\delta x, \delta y) \cdot F(x + \delta x, y + \delta y) \Biggr) + {w_{out}}_{bias}\]

• 앞에서 살펴본 parameter의 갯수를 생각해 보면 kernel의 갯수가 늘어나면 그 늘어난 양에 비례하여 parameter의 갯수가 늘어나는 것을 알 수 있습니다.
• kernel의 갯수가 늘어나면 parameter의 갯수가 늘어나고 parameter의 갯수가 늘어나면 element-wise multiplication을 해야 할 연산의 갯수 또한 늘어납니다. 따라서 연산량이 늘어서 처리 속도 또한 늘어나게 됩니다.

• kernel의 갯수를 늘린 것 처럼 Input의 갯수를 늘려보겠습니다. 예를 들어 일반적으로 사용하는 RGB와 같은 3채널로 늘려보겠습니다

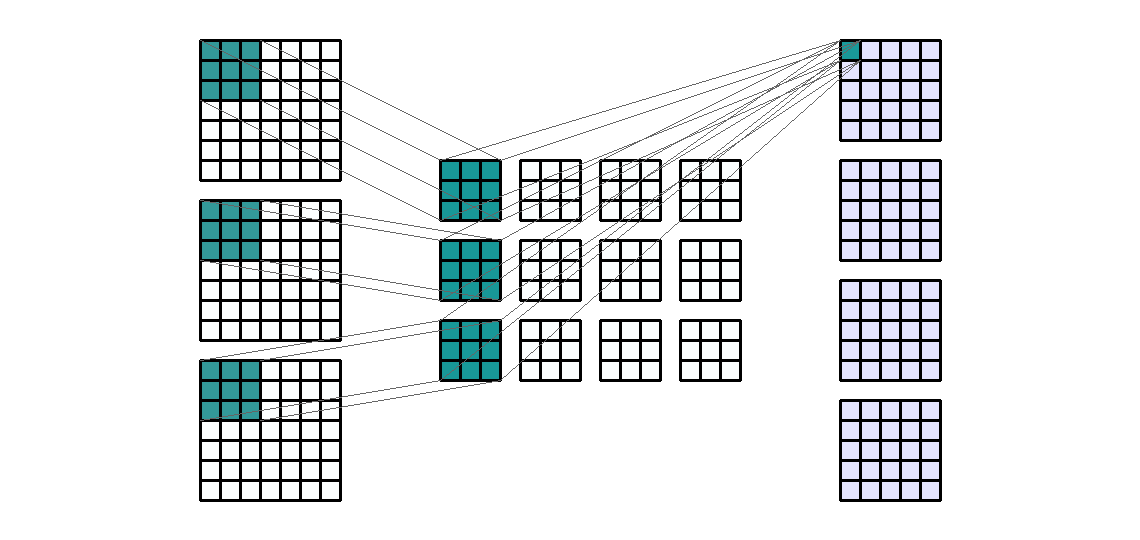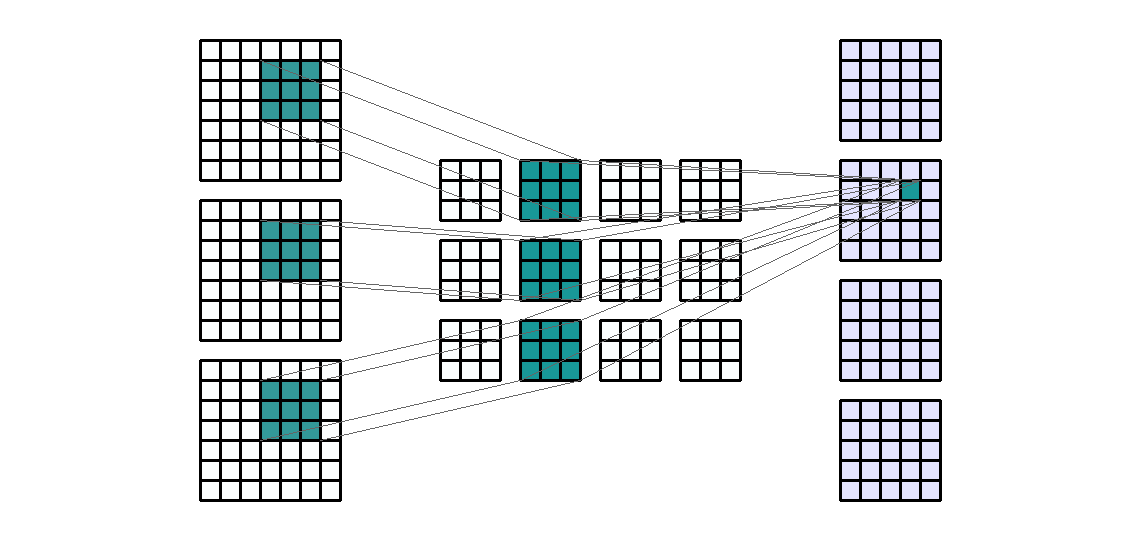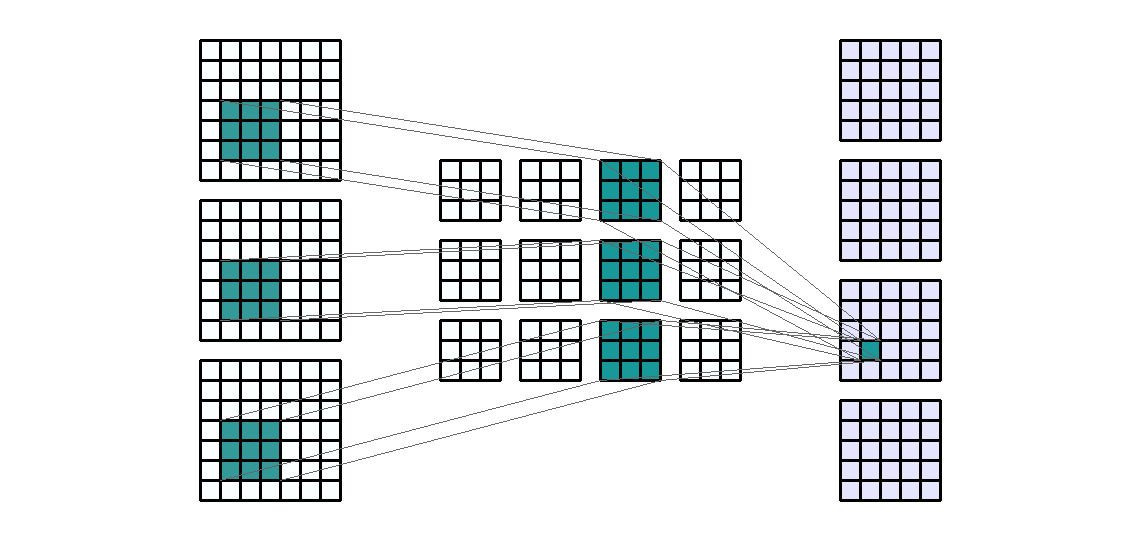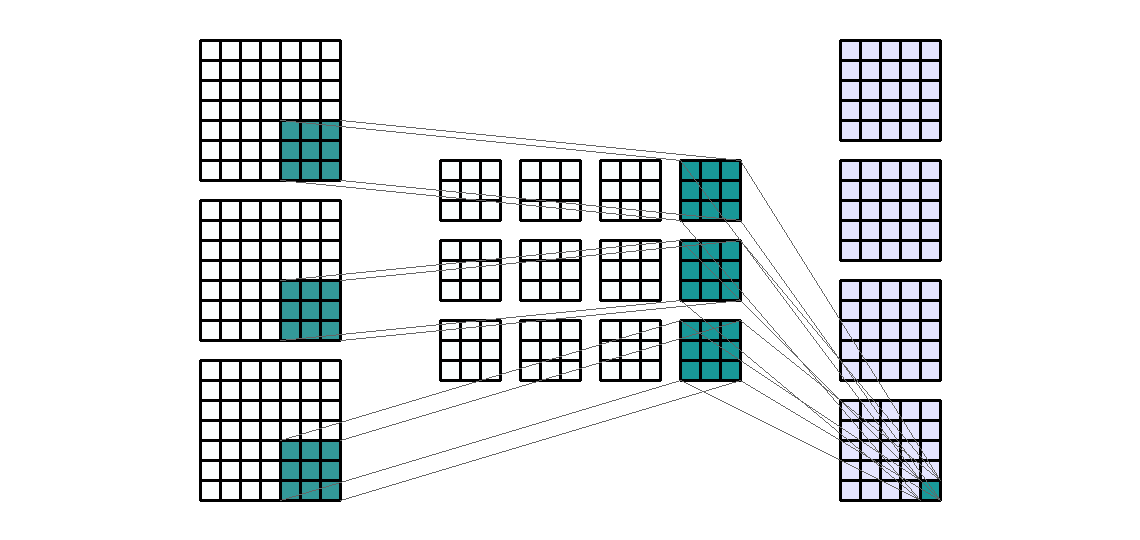
• Input shape : (7, 7, 3)
• Output shape : (5, 5, 4)
• Kernel shape : (3, 3)
• Stride : (1, 1)
• Padding : (0, 0)
• Dilation : (1, 1)
• Group : 1

• Input의 갯수가 n개로 늘어나면 같은 kernel이 n번의 convolution 연산이 발생하게 됩니다.
• 위 그림에서 kernel은 총 12개 입니다. 먼저 Input의 각 channel에 kernel이 element-wise multiplication을 하게 됩니다. 이 때, Input의 갯수 만큼의 kernel이 연산에 사용됩니다.
• 그 다음 필요한 Output의 채널 만큼 이 연산을 반복합니다. 위 예제에서 Output의 채널 수는 4이므로 4번을 반복하게 됩니다.
• 따라서 사용된 kernel의 갯수는 12개가 됩니다. (Input의 채널 수 * Output의 채널 수)
• 수식으로 정리하면 다음과 같습니다.

• \[G_{out}(x, y) = \sum_{in=0}^{N_{in}} w_{out, in} * F_{in}(x, y) = \sum_{in=0}^{N_{in}}\Biggl( \Biggl( \sum_{\delta x = -k_{i}}^{k_{i}} \sum_{\delta y = -k_{j}}^{k_{j}} w_{out, in}(\delta x, \delta y) \cdot F_{in}(x + \delta x, y + \delta y) \Biggr) + {w_{out, in}}_{bias} \biggr)\]

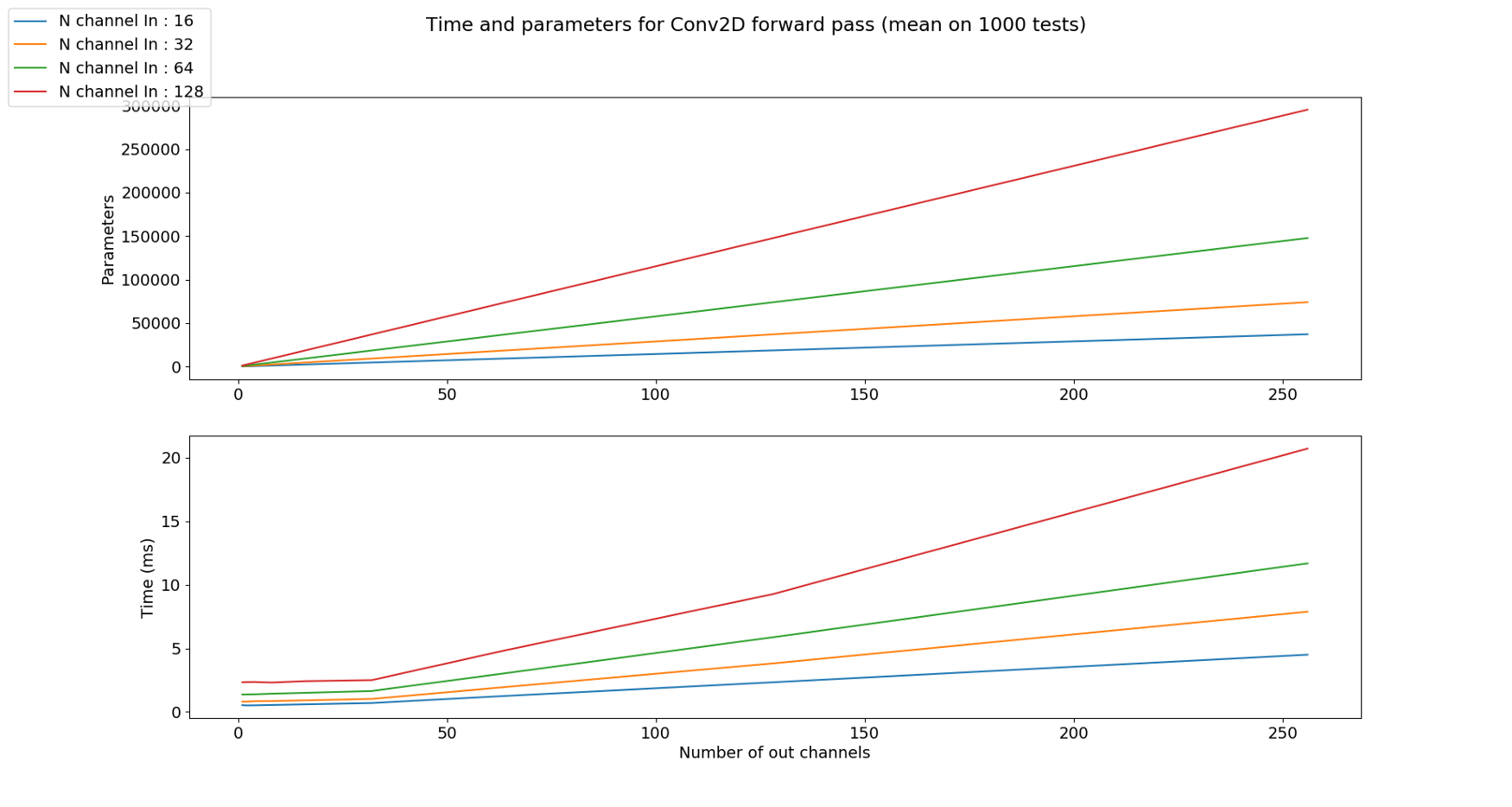
• 앞에서 다룬 내용을 생각해 보면 kernel의 갯수가 늘어남에 따라 parameter 수와 수행 시간이 늘어난다는 것을 확인하였습니다.
• 즉, Input channel의 갯수가 늘어나면 kernel의 갯수가 늘어나게 되므로 parameter와 수행시간이 늘어나게 됨을 유추할 수 있습니다. 아래 그림을 통해 확인해 보면 됩니다.

Kernel의 size 란

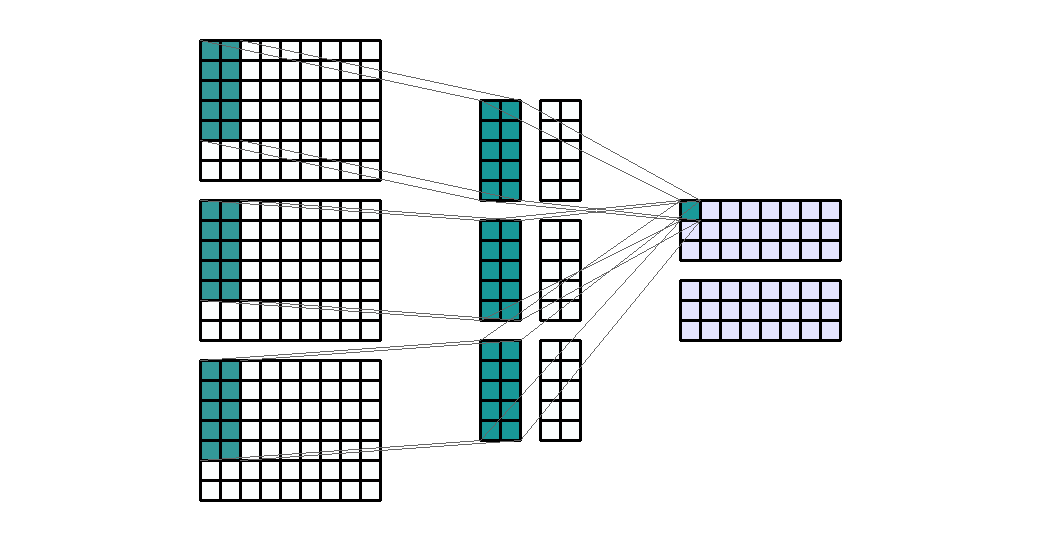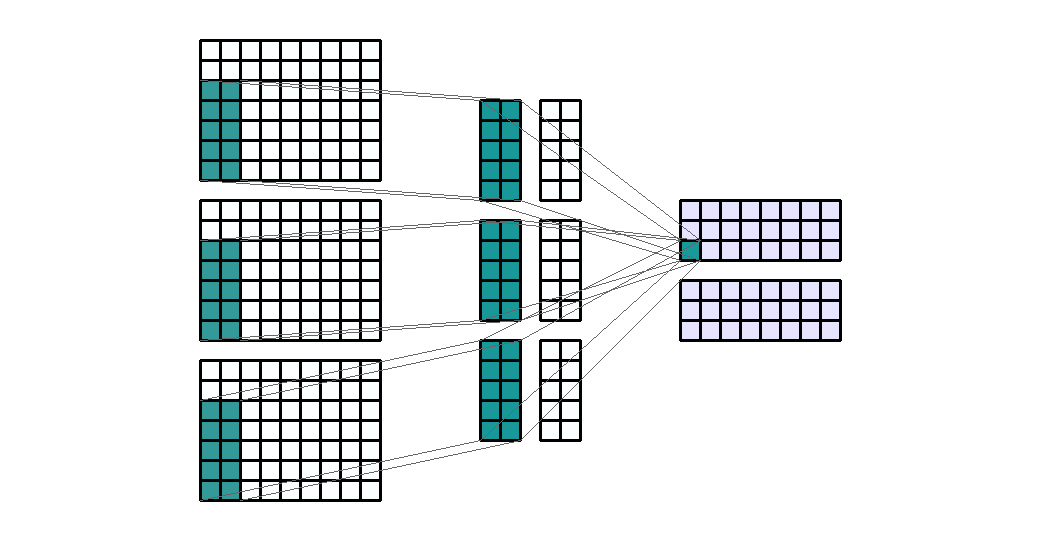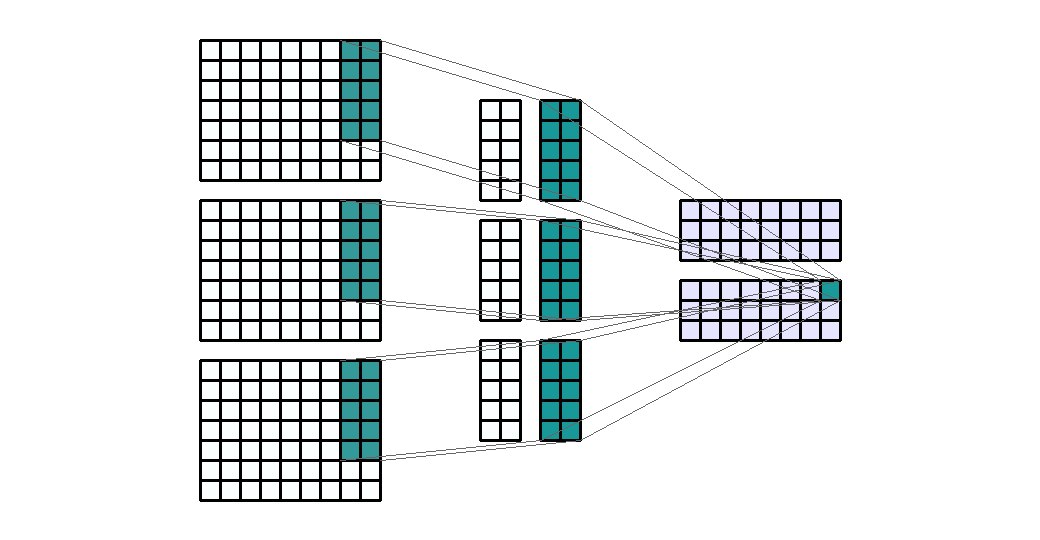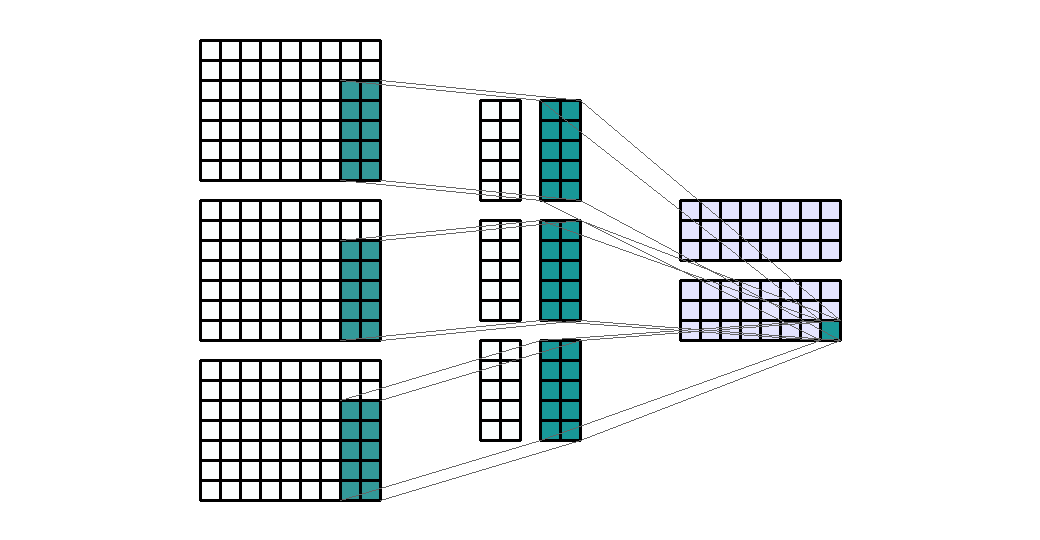
• Input shape : (7, 9, 3)
• Output shape : (3, 9, 2)
• Kernel shape : (5, 2)
• Stride : (1, 1)
• Padding : (0, 0)
• Dilation : (1, 1)
• Group : 1

• 앞의 모든 예제에서 kernel의 크기를 (3, 3)을 사용하였습니다. 어떤 커널의 크기를 사용하는 지는 딥러닝 네트워크 설계에 달려있습니다. 다만 지금까지 연구되어 온 바로는 (3, 3)을 여러개 사용하는 것이 (5, 5), (7, 7)과 같이 큰 네트워크를 사용하는 것에 비해 효과가 좋다고 알려져 있기 때문에 (3, 3)의 크기의 kernel이 일반적으로 사용되고 있습니다.
• 바로 위 예제에서는 일반적인 (3, 3) 크기의 kernel 대신 (5, 2)라는 다소 특이한 크기의 kernel을 예제로 사용해 보았습니다. 목적만 뚜렷하다면 height, width의 크기가 달라도 상관없습니다.
• 특히 kernel의 사이즈를 height, width 모두 홀수를 사용하는 것은 중앙의 pixel 점을 기준으로 대칭적으로 만들기 위함입니다. 대칭적으로 만들어야 연산할 때 고려할 점이 줄어들기 때문이며 물론 목적만 뚜렷하다면 짝수의 크기를 사용해도 상관없습니다.

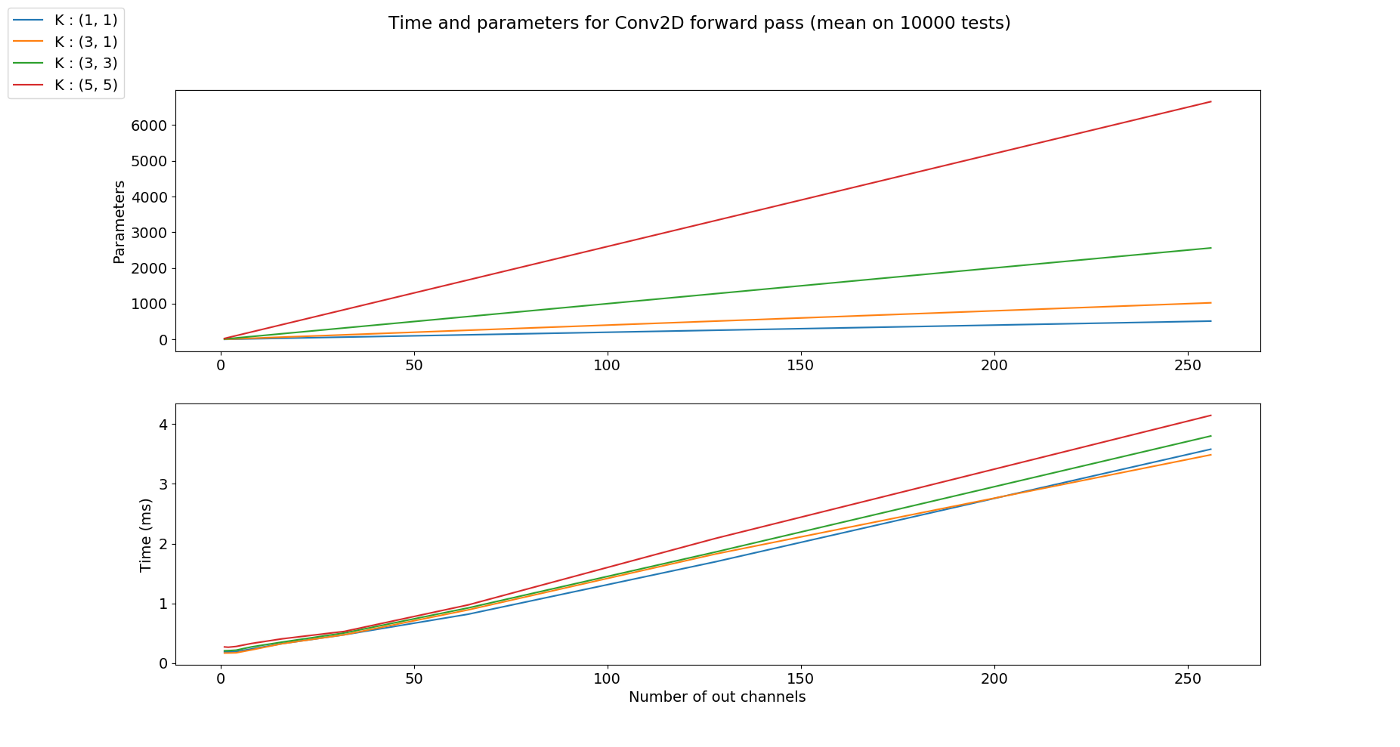
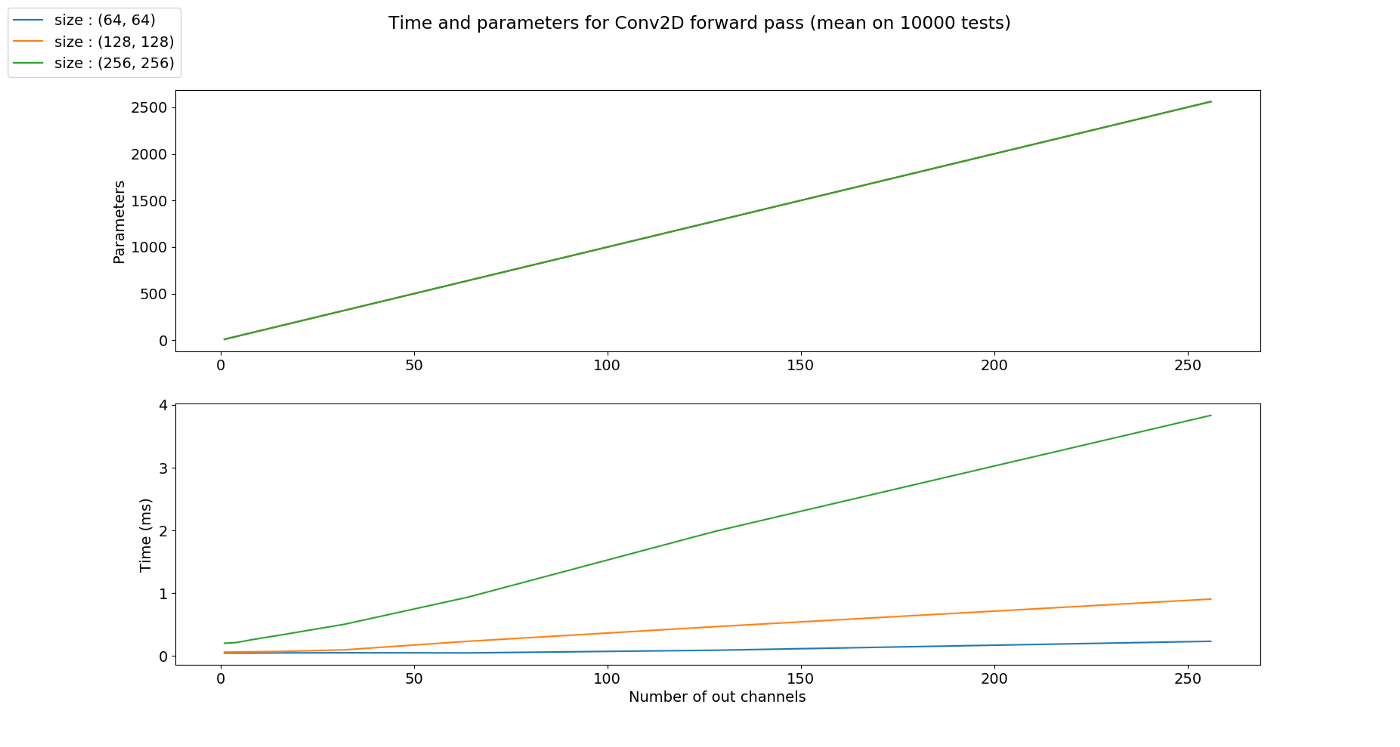
• 위 그래프를 해석하면 kernel의 사이즈가 커질수록 파라미터의 갯수가 늘어나는 것을 볼 수 있습니다.
• 수행 시간을 비교해 보았을 때 kernel의 사이즈가 클 수록 (파라미터의 갯수가 늘어났기 때문에) 수행 시간이 커지는 것을 알 수 있습니다.

Stride 란

• 지금 까지 Input과 kernel을 연산할 때, kernel을 1픽셀 씩 left → right 방향으로 옮기고 1픽셀 씩 top → bottom 방향으로 옮겼습니다.
• kernel을 옮기는 크기가 stride 입니다. 즉, 위에서 살펴본 모든 예제는 stride가 (1, 1)의 크기를 가지는 것으로 height의 방향(top → bottom)으로 1, width의 방향(left → right)으로 1을 적용하였었습니다.
• 아래 예제에서는 stride를 (1, 3)의 크기로 적용해 보겠습니다. 즉, width의 방향으로는 픽섹을 3칸씩 이동합니다.

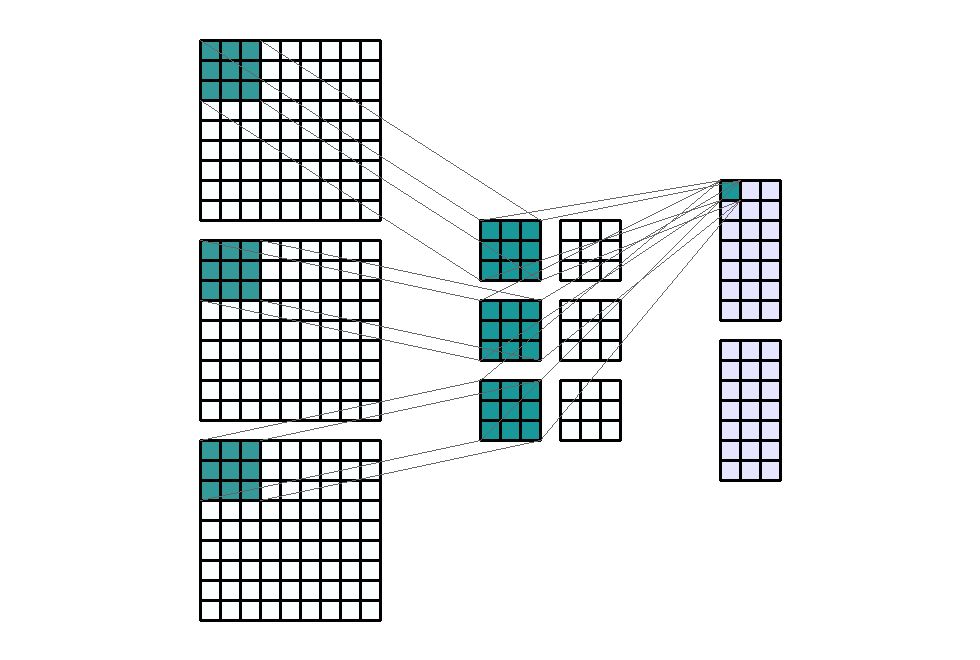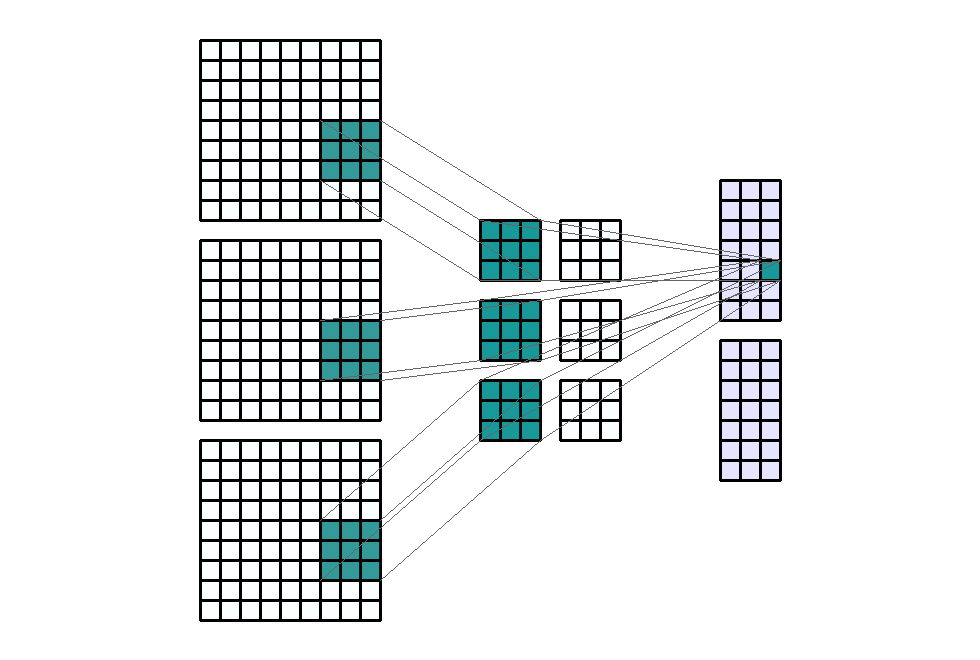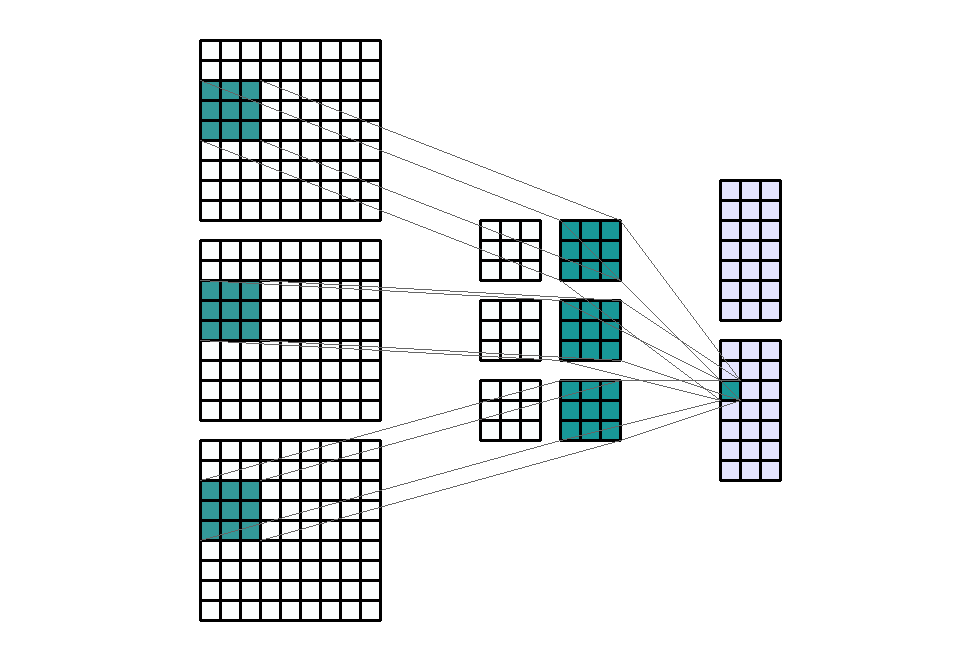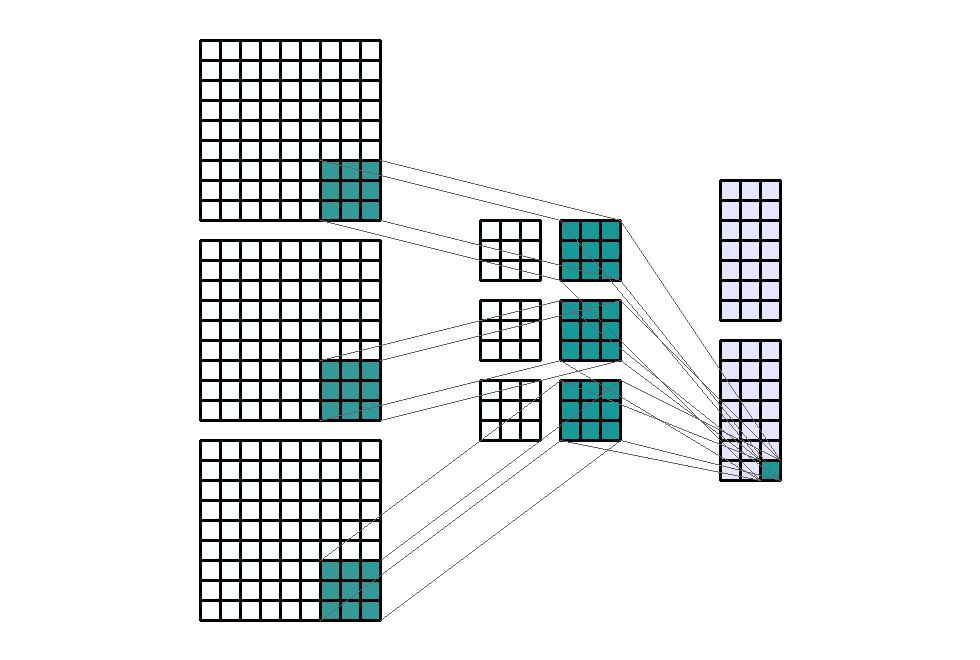
• Input shape : (9, 9, 3)
• Output shape : (7, 3, 2)
• Kernel shape : (3, 3)
• Stride : (1, 3)
• Padding : (0, 0)
• Dilation : (1, 1)
• Group : 1

• stride의 사용 목적은 downsampling 입니다. 즉, Output의 shape을 줄이기 위함입니다.
• 하지만 위 연산 과정을 보면 stride의 크기를 늘리면 output의 shape이 작아지기는 하지만 parameter의 수는 그대로 인 것을 확인할 수 있습니다.

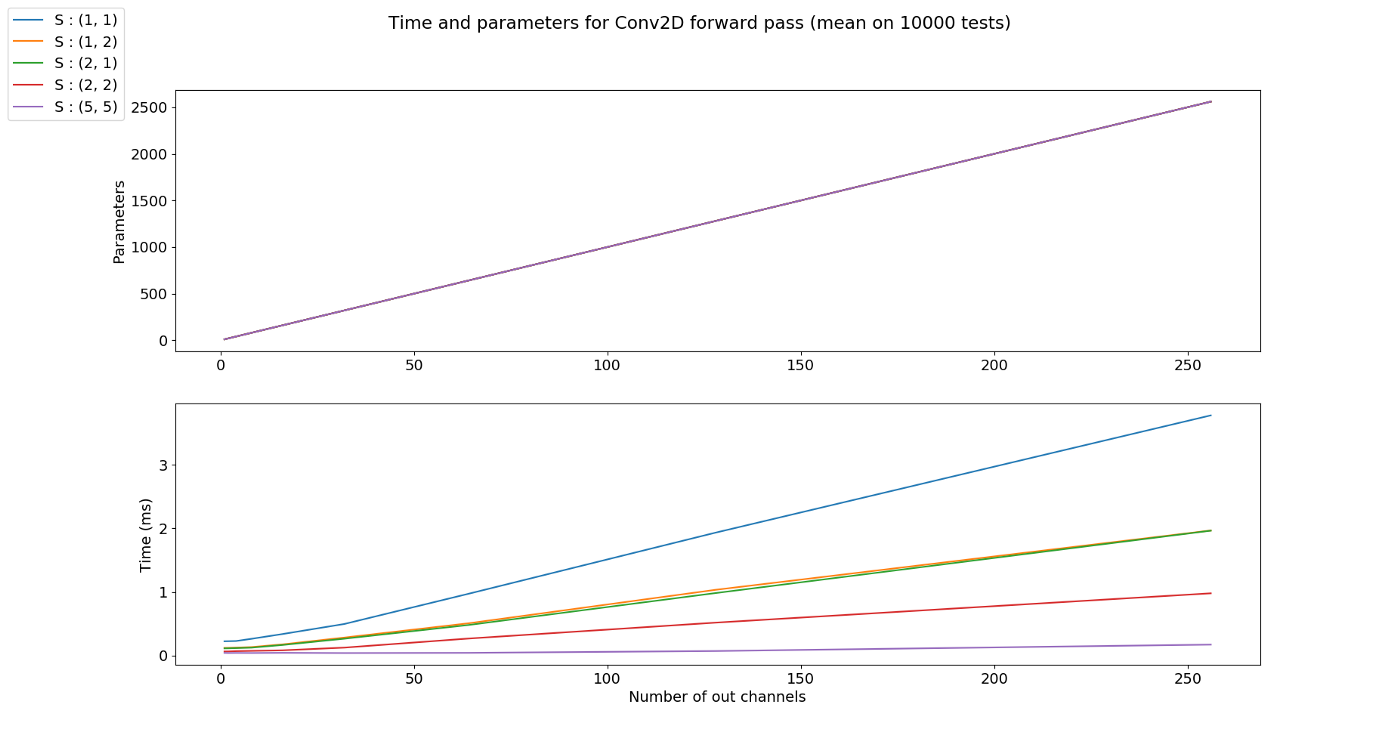
• 위 그래프 처럼 stride의 크기가 변경되더라도 파라미터의 갯수는 모두 같습니다. 하지만 stride의 크기가 커질수록 output이 downsampling 되어서 수행 시간이 줄어드는 것을 알 수 있습니다.

Padding 이란

• padding은 convolution 연산을 하기 전에 intput의 가장자리에 추가된 픽셀 수를 나타냅니다. 일반적으로 padding 픽셀은 0으로 설정됩니다.
• 지금 까지 살펴본 예시들을 보면 padding이 모두 0이었기 때문에 convolution 연산을 하면 가장자리의 크기가 줄어들었습니다. 반면 아래 예제를 한번 살펴보도록 하겠습니다.

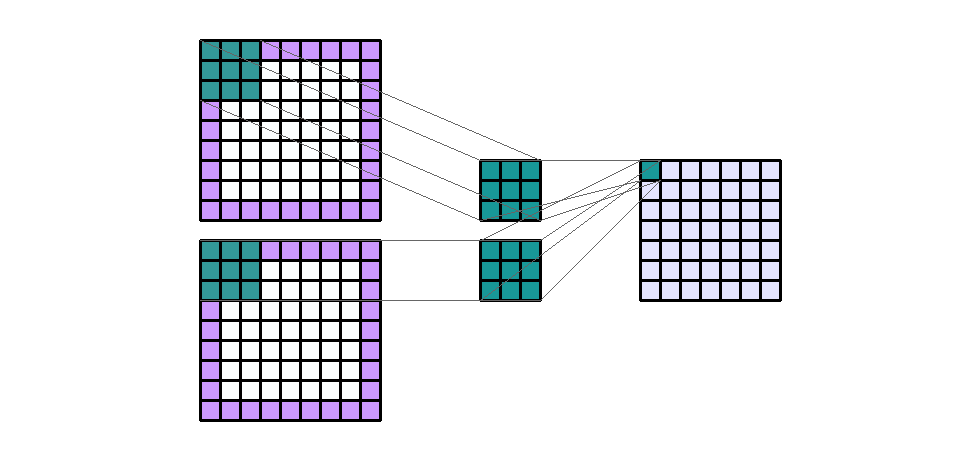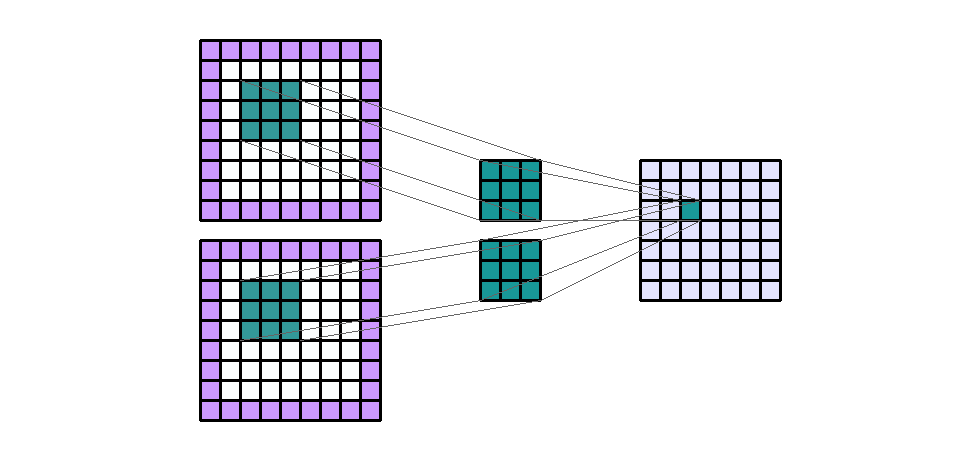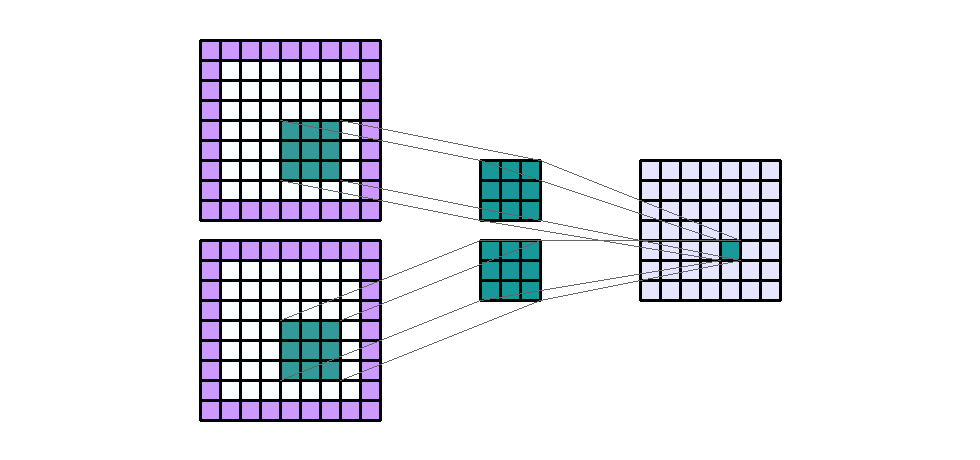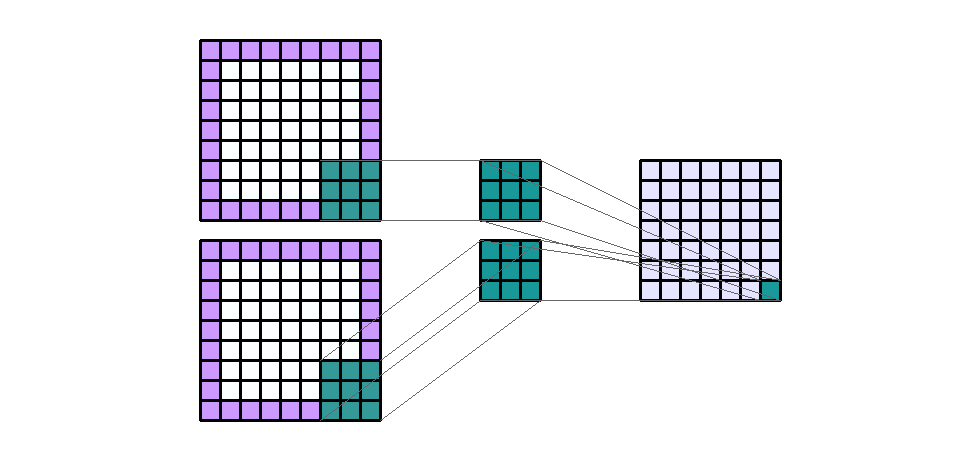
• Input shape : (7, 7, 2)
• Output shape : (7, 7, 1)
• Kernel shape : (3, 3)
• Padding : (1, 1)
• Stride : (1, 1)
• Dilation : (1, 1)
• Group : 1

• 여기서 주목할 점은 Input과 Output의 height와 width의 크기가 그대로 유지되었다는 점입니다. padding을 사용하는 가장 큰 목적 중 하나가 바로 input과 output의 크기를 유지하기 위함입니다.
• 특히 input, output 크기를 유지해야할 때, kernel의 사이즈가 (3, 3), padding (1, 1)은 짝으로 사용되니 알아두면 유용합니다.

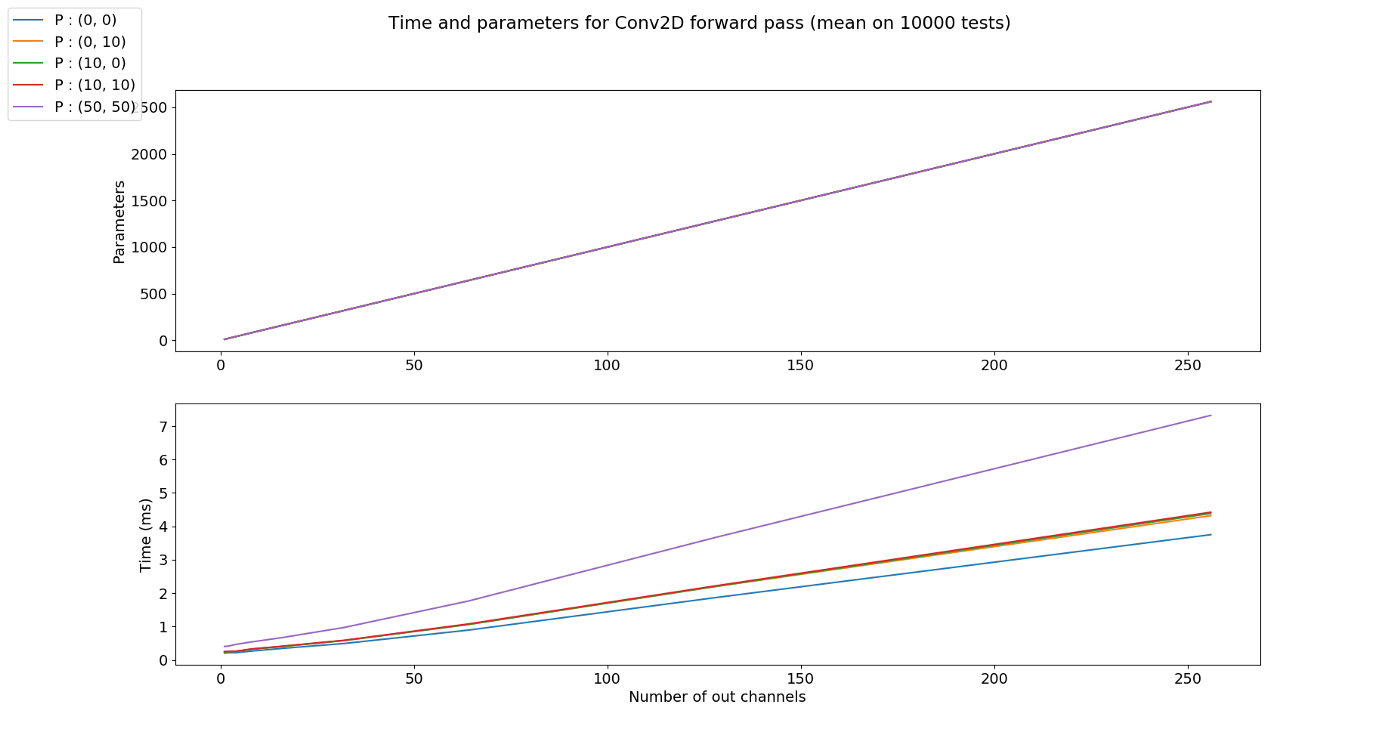
• 앞의 stride와 같은 이유로 padding은 output의 크기를 조절하는 역할을 할 뿐 파라미터의 수와 상관 없습니다.
• 따라서 위 그래프 처럼 padding의 크기에 상관없이 파라미터의 수는 같지만 padding의 크기가 커질수록 수행시간은 커지게 됨을 알 수 있습니다.
• padding을 할 때, 추가적으로 생성된 가장자리에 어떤 값을 넣을 지는 어떤 padding을 사용하는 지에 따라 다릅니다. zero padding의 경우 0의 값을 넣는 반면 가장자리의 값을 그대로 복사하는 경우도 있고 interpolation 하는 방법으로 값을 넣을 수도 있습니다.

Dilation 이란

• 이번에는 dilation에 대하여 알아보겠습니다. dilation은 kernel의 한 픽셀에서 다른 픽셀 까지의 거리를 나타냅니다.
• 지금 까지 살펴본 예제들을 보면 모두 dilation은 (1, 1) 이었습니다. 즉, 한 픽셀에서 다른 픽셀 까지 거리가 1로 바로 옆에 붙어있었기 때문입니다. 반면 다음 예제를 한번 살펴보겠습니다.

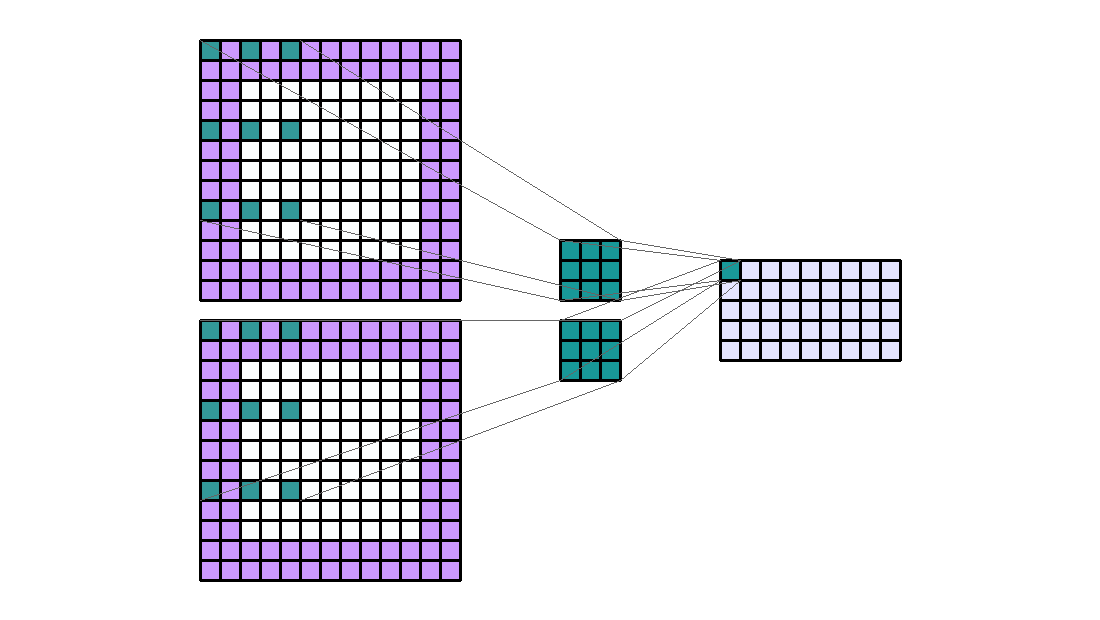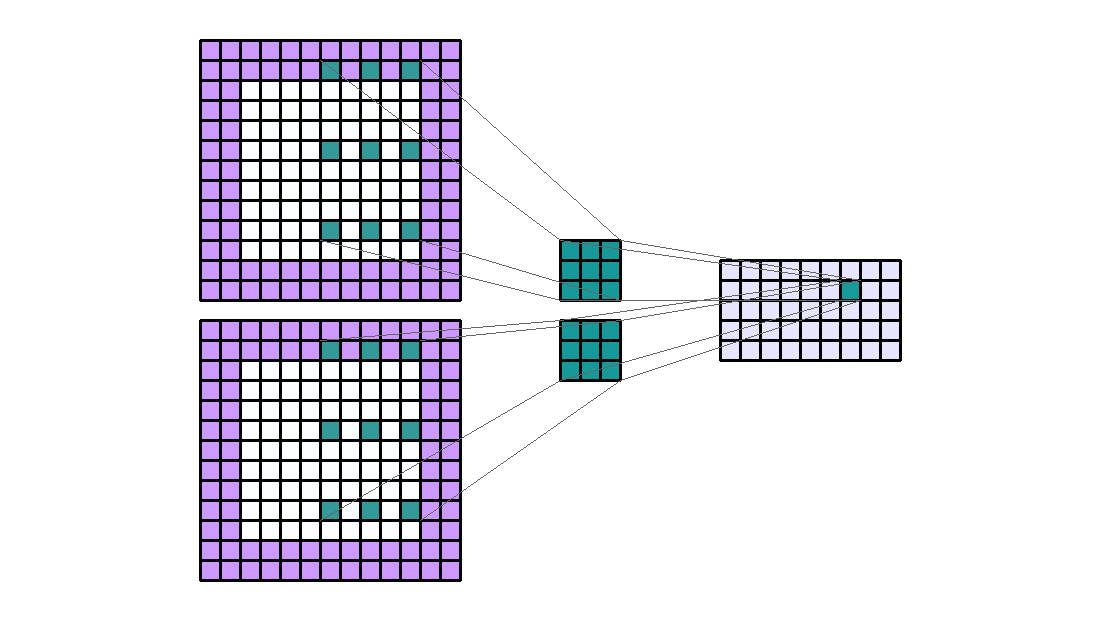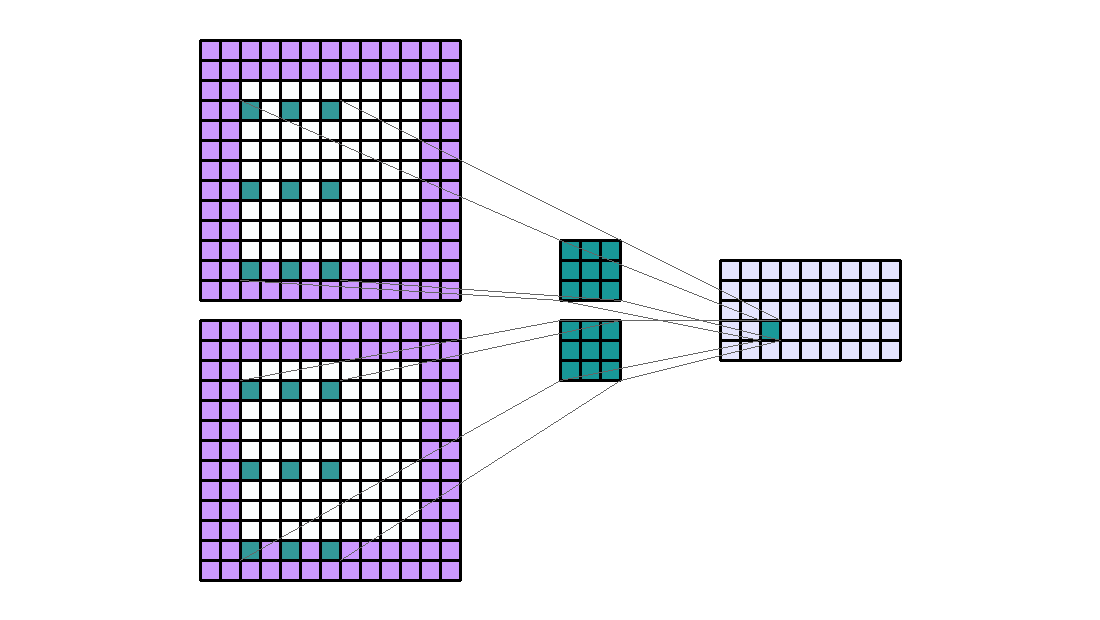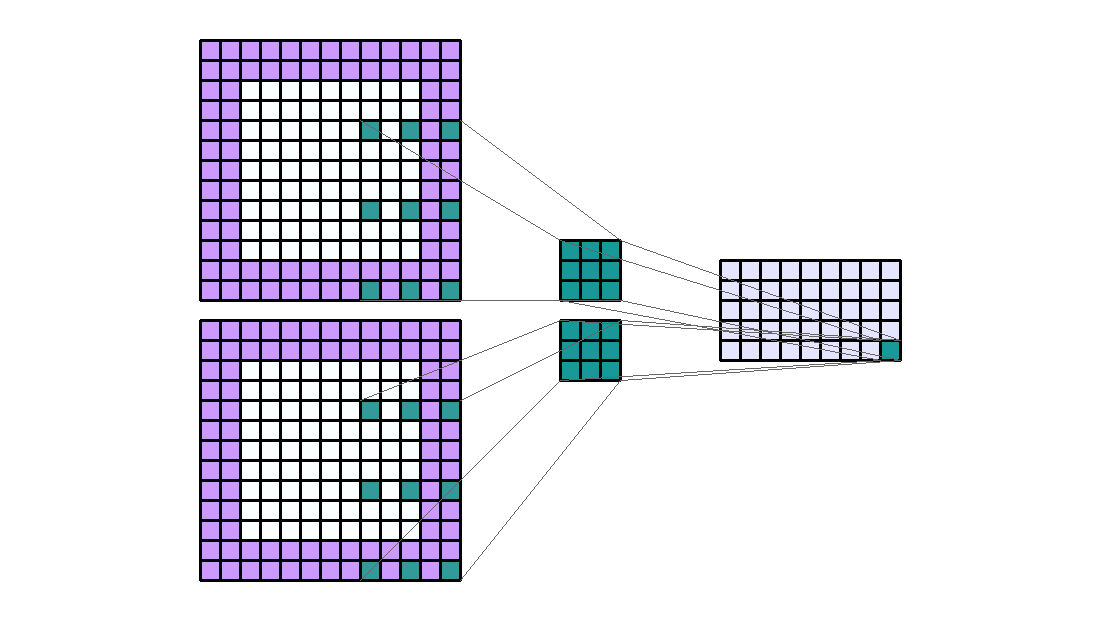
• Input shape : (9, 9, 2)
• Output shape : (5, 9, 1)
• Kernel shape : (3, 3)
• Stride : (1, 1)
• Padding : (2, 2)
• Dilation : (4, 2)
• Group : 1

• 위 예제의 dilation은 (4, 2) 입니다. 즉, Input과 계산되는 kernel에서 한 픽셀에서 바로 옆의 픽셀 까지의 height 방향으로 4칸 이동해야 하고 width 방향으로 2칸 이동해야 한다는 뜻입니다.
• 이와 같은 방법을 사용하는 이유는 receptive field를 넓히기 위함입니다. 즉, kernel이 한번에 넓은 영역을 보고 학습할 수 있다는 뜻입니다.
• 만약 dilation이 (1, 1)이면 kernel의 receptive field는 (3, 3)이지만 위 처럼 (4, 2)의 dilation을 적용하면 (4 * (3 - 1) + 1, 2 * (3 - 1) + 1) = (9, 5)가 됩니다.

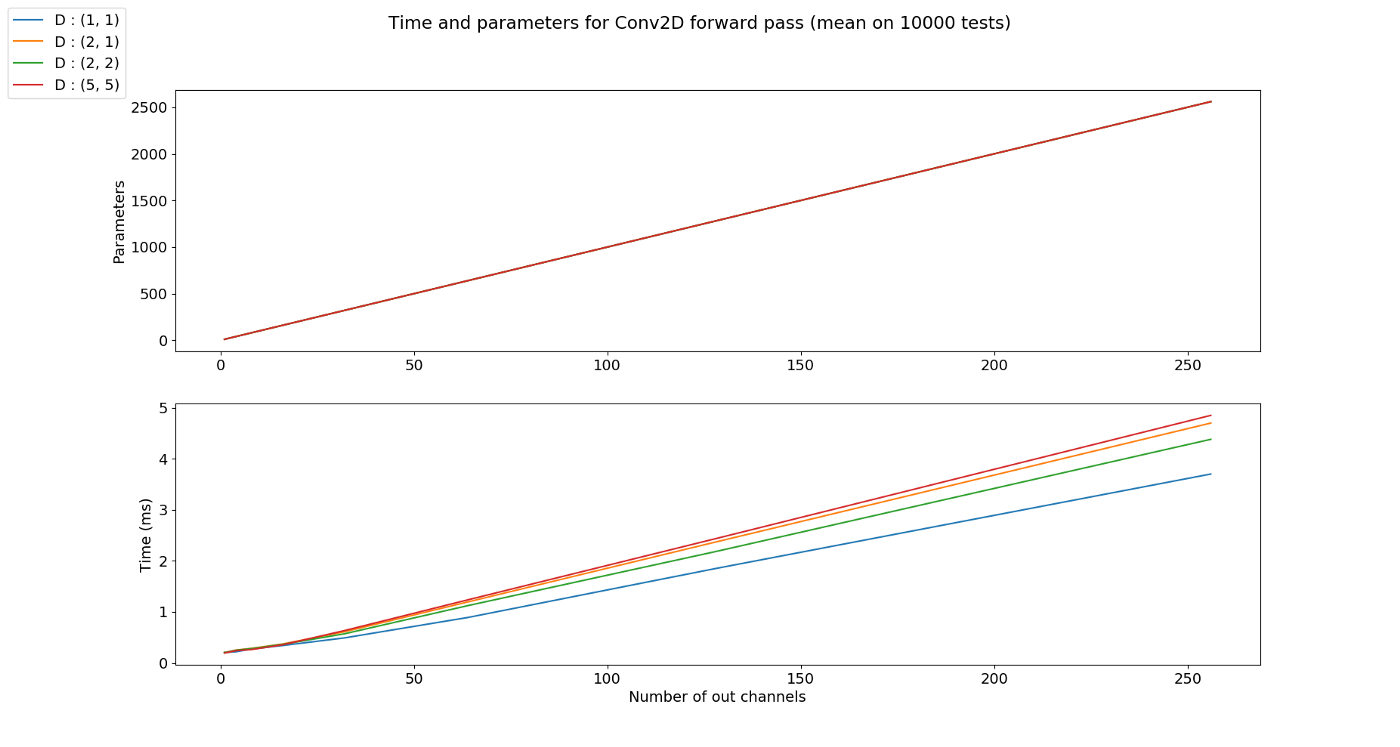
• 앞에서 다룬 stride와 padding과 같이 dilation 또한 kernel의 수에 직접적인 영향을 주진 않습니다.
• stride, padding에 비해 연산량 변화에 대한 영향도 미미합니다.

Group 이란

• 이번에 다루어 볼 것은 group 입니다. group은 channel과 연관이 있습니다.
• 앞에서 다룬 내용들을 보면 Input의 모든 channel과 kernel이 element-wise multiplication 연산을 한 뒤 합하여 1개의 scalar 값이 되어 output의 한 픽셀 값이 되었습니다. 여기서 모두 합하여 1개의 값으로 만든다는 것이 group이 1이라는 뜻입니다.
• 만약 Input channel이 10이고 group이 5라면 element-wise multiplication 연산한 결과를 차례 대로 2개씩 묶어서 5쌍을 만들 수 있습니다. 그러면 Output이 5개가 나오게 됩니다. 예제를 한번 살펴보겠습니다.

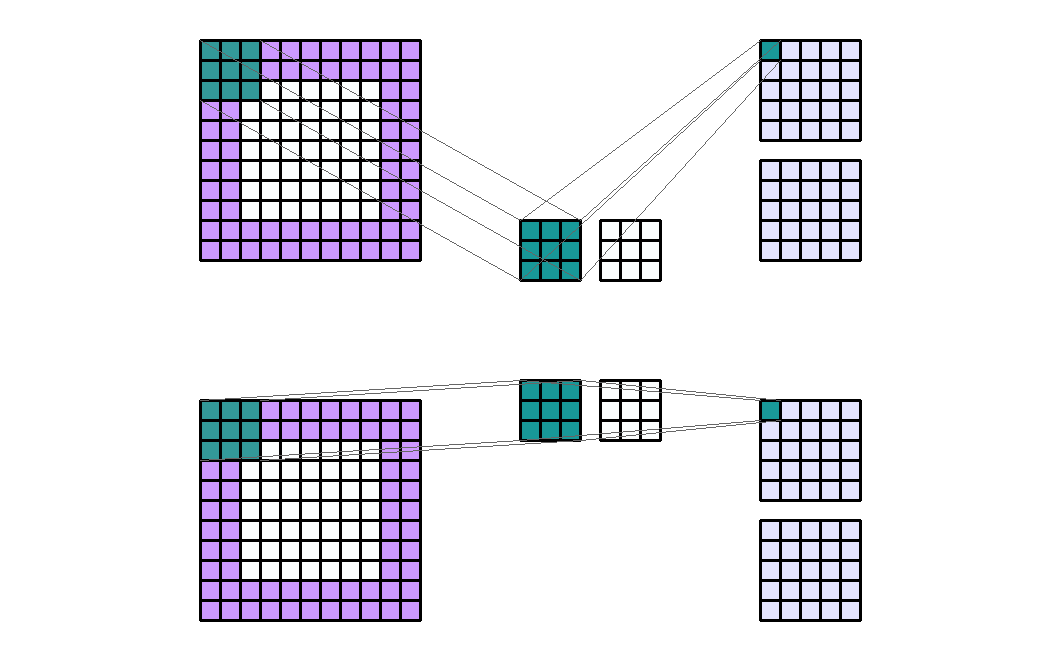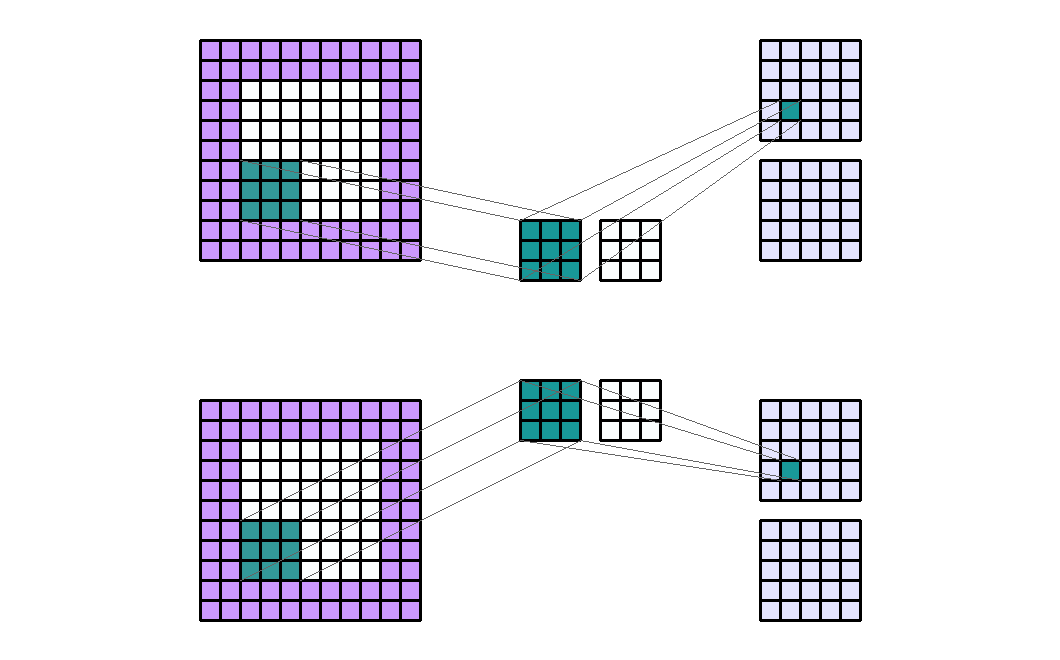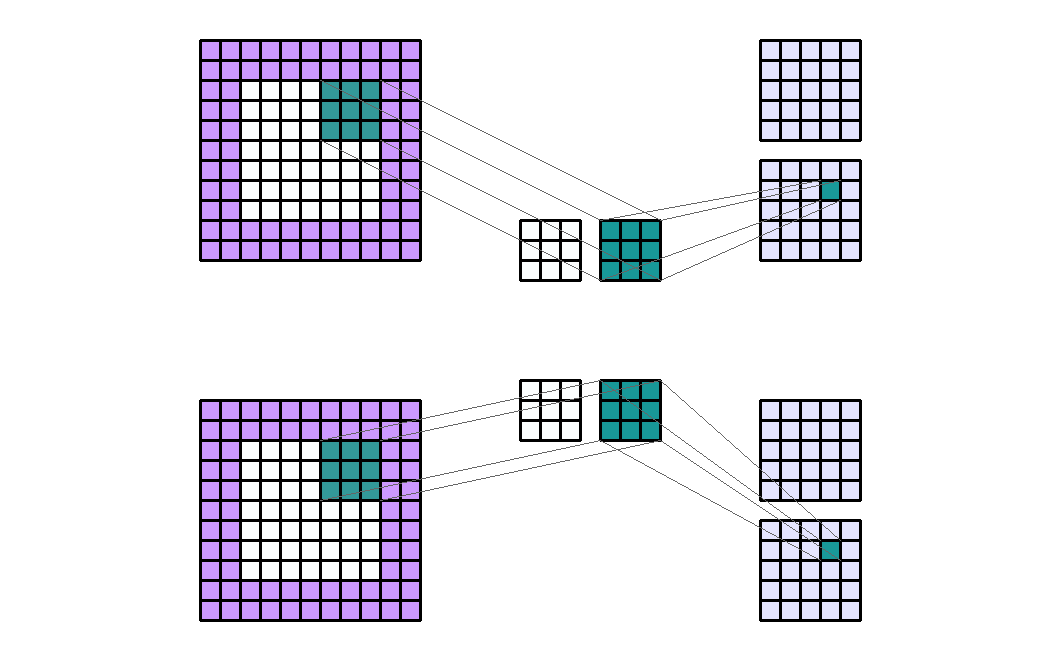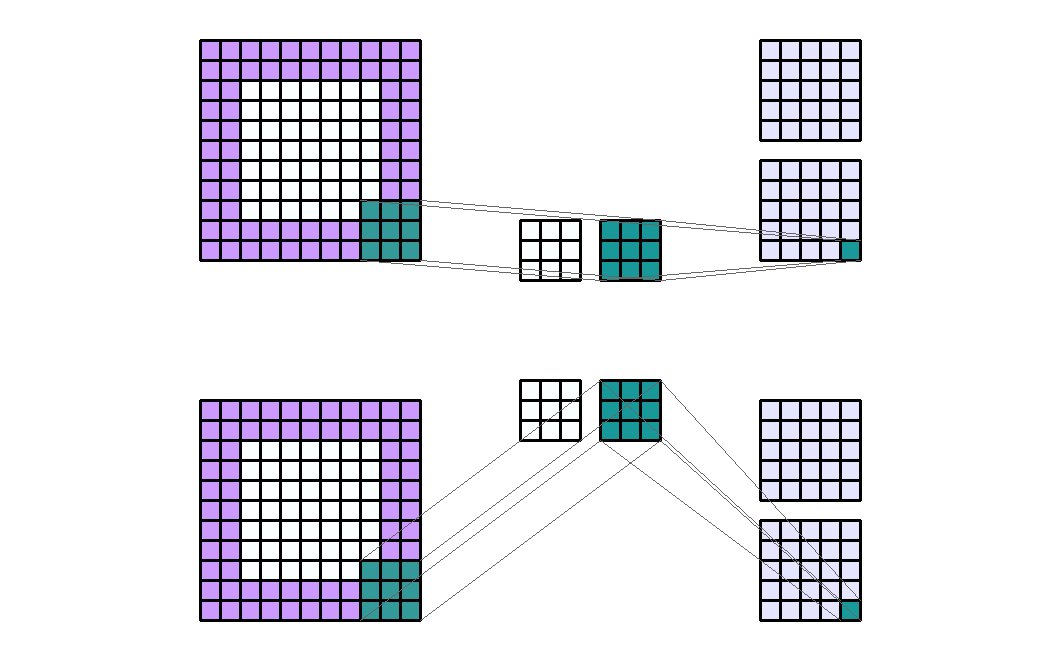
• Input shape : (7, 7, 2)
• Output shape : (5, 5, 4)
• Kernel shape : (3, 3)
• Stride : (2, 2)
• Padding : (2, 2)
• Dilation : (1, 1)
• Group : 2

• 위 예제를 보면 Input의 channel이 2이고 Group이 2 그리고 kernel 셋이 2개가 있기 때문에 Output의 channel이 4가 됨을 알 수 있습니다.
• 이렇게 group을 나누는 이유를 보면 다양한 이유가 있을 수 있습니다. 예를 들어 kernel을 연산한 결과를 하나로 합해야 할 이유가 없을 때가 있을 수 있습니다. 즉, Input의 channel 마다 성질이 달라 independent 하다면 element-wise multiplication 결과를 굳이 하나로 합칠 필요가 없습니다.
• 또는 mobilenet 에서 사용되는 depthwise separable 연산과 같이 파라미터의 수를 줄이기 위해서도 사용될 수 있습니다. 위 예제를 보시다 시피 kernel 이 공유되어서 사용되기 때문입니다.
• 계산 측면에서도 이와 같은 group convolution은 효율적입니다. 왜냐하면 나뉘어진 group를 병렬로 계산할 경우 그 효율성이 더 높아지기 때문입니다.
• Group Convolution을 사용할 때, 보통 pytorch와 같은 framework에서는 Input과 Output의 크기를 정한 뒤 group을 지정해줍니다. 이 때, 주의해야 할 점은 연산을 하기 위해 group이 반드시 Input의 channel과 output의 channel의 공약수이어야 한다는 점입니다.

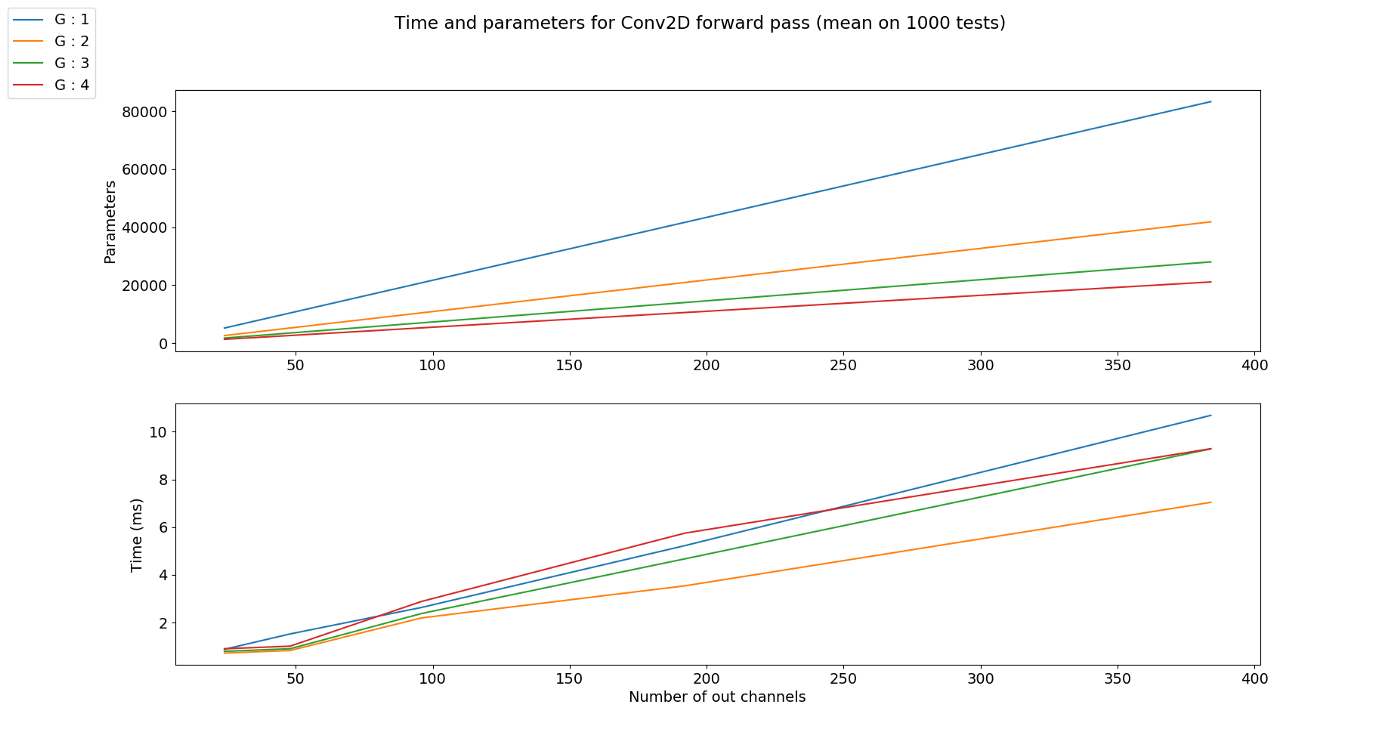
• chnnel은 고정일 때, group의 갯수가 커지면 공유되는 kernel의 수가 많아지므로 파라미터의 갯수는 줄어들게 됩니다.
• 단순히 파라미터의 갯수가 줄어들면 연산해야 할 양이 작아진다고 생각을 하였었는데 이번에는 조금 다릅니다. 파라미터의 갯수는 줄었지만 output의 channel 수는 오히려 늘어날 수 있기 때문입니다. 위 그래프를 참조하시기 바랍니다.

Output Channel Size 란

• 앞에서 다룬 모든 argument 들을 집합하여 Input의 height와 width가 주어졌을 때, Output의 height와 width를 계산하려면 다음과 같이 정리할 수 있습니다.
• 앞의 내용들을 모두 이해하였다면, 식을 이해하는 데 어려움을 없을 것입니다.

• \[H_{out} = \Bigl\lfloor \frac{H_{in} + 2P_{H} - D_{H}(K_{H}-1) - 1}{S_{H}} + 1 \Bigr\rfloor\]
• \[W_{out} = \Bigl\lfloor \frac{W_{in} + 2P_{W} - D_{W}(K_{W}-1) - 1}{S_{W}} + 1 \Bigr\rfloor\]

Basic Convolution Operation

• 지금부터는 앞에서 배운 convolution 연산의 기본적인 성질들을 이용하여 다양한 convolution 연산에 대하여 다루어 보도록 하겠습니다.
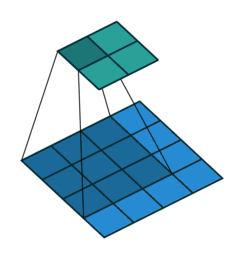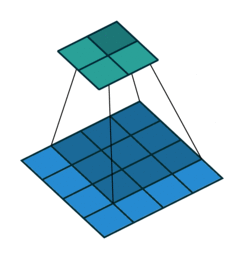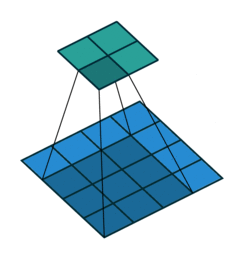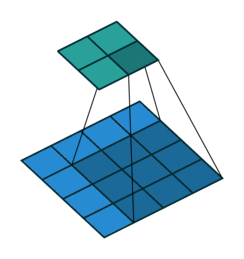
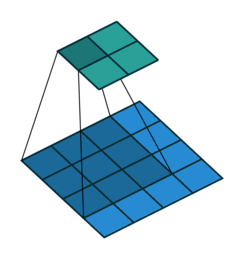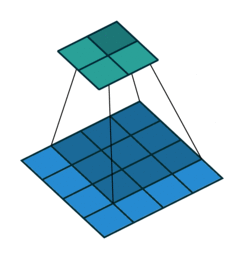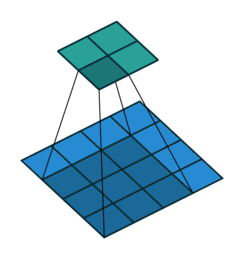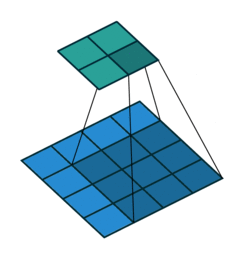
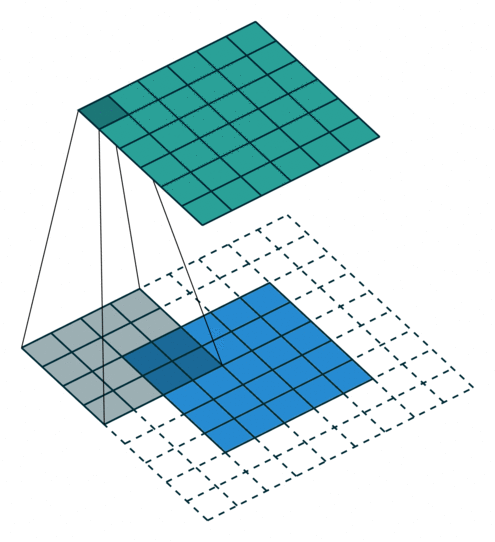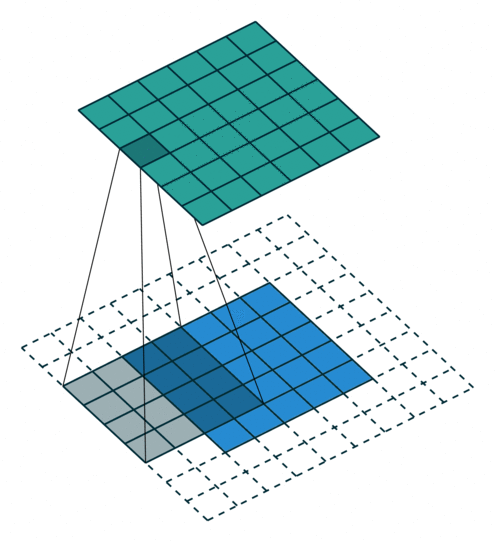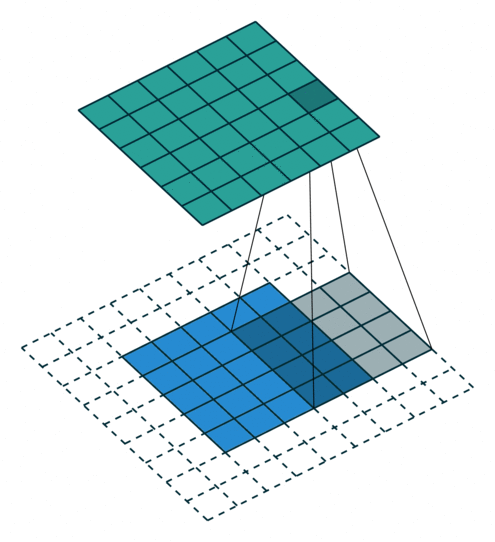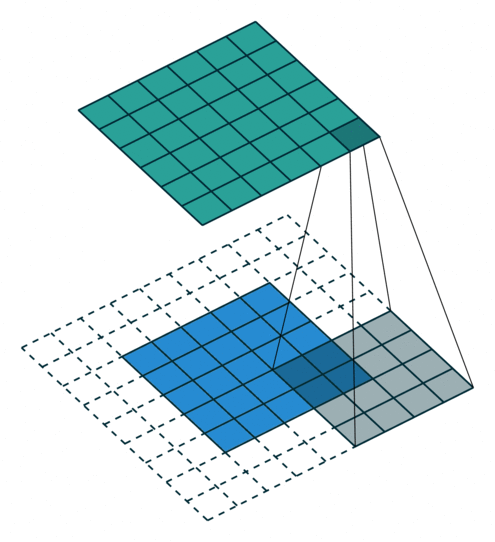
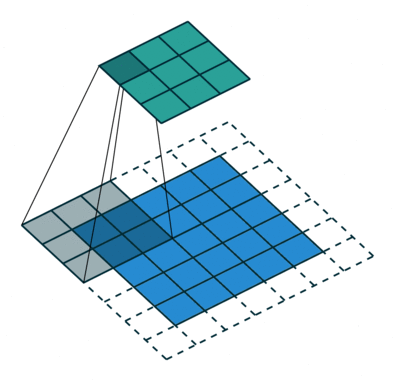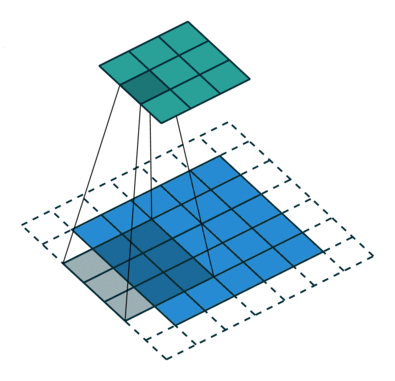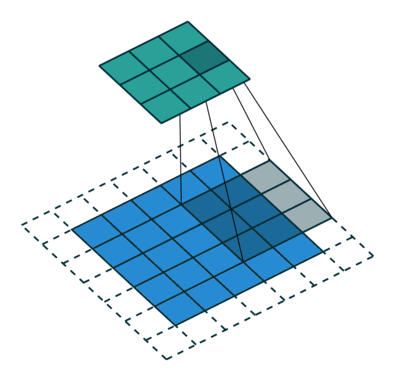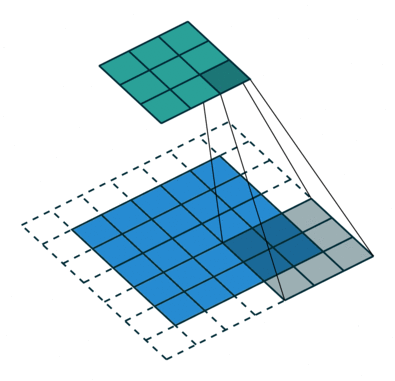
• 아래 애니메이션의 파란색이 인풋이고 청록색이 아웃풋입니다.
• Convolution 연산을 이용하면 input의 feature를 압축하게 되므로 convolution 연산 이후의 feature map의 크기는 더 줄어들게 됩니다.
• 아래 애니메이션들도 보면 파란색의 인풋이 convolution 연산을 거치면서 청록색 아웃풋 처럼 사이즈가 작아지게 된 것을 볼 수 있습니다.

No padding, No strides

Arbitrary padding, No strides

Half padding, no strides

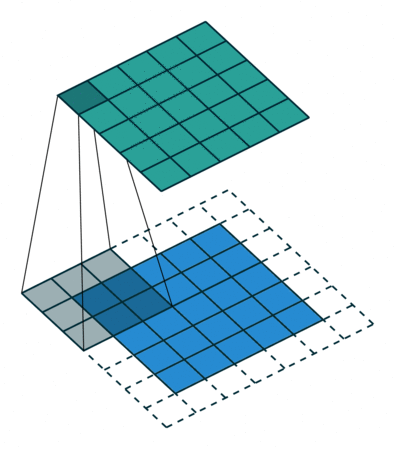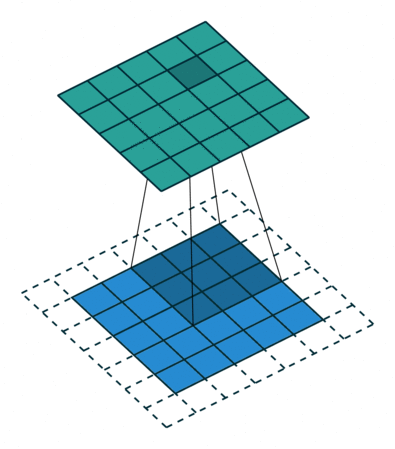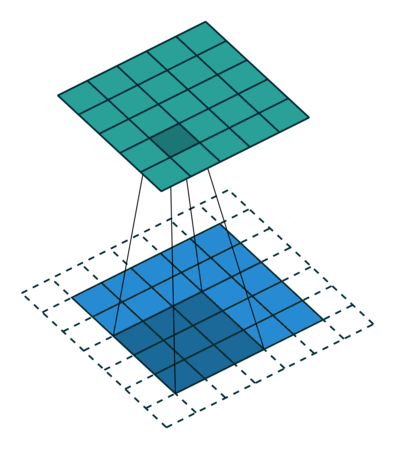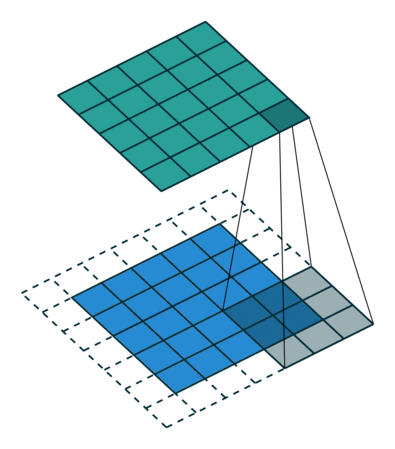
• 위 경우에는 입력과 출력의 크기가 같아지는 것을 확인할 수 있습니다. 이 방법이 입/출력의 크기를 동일하게 유지하기 위해 많이 사용하는 방법입니다.

Full padding, No strides

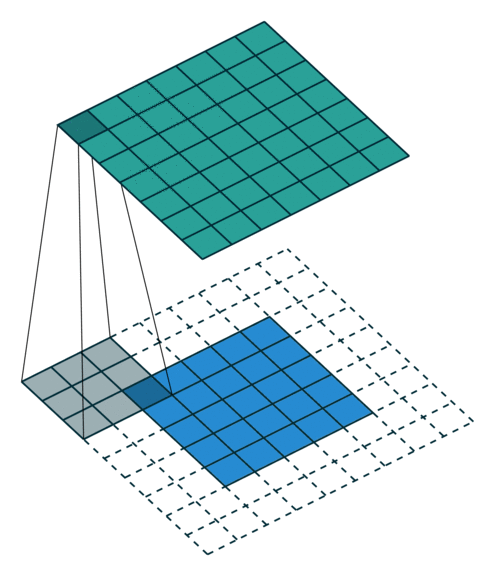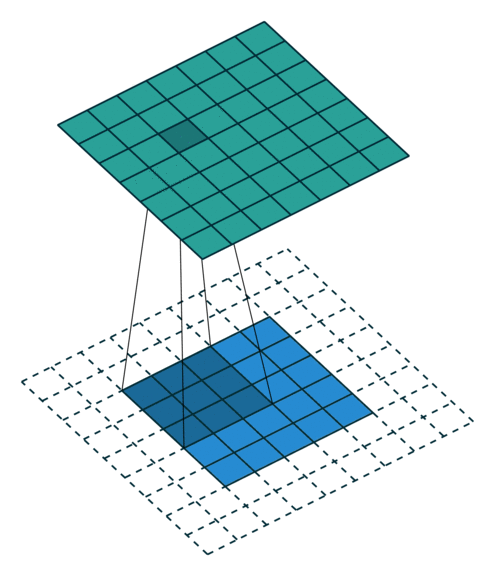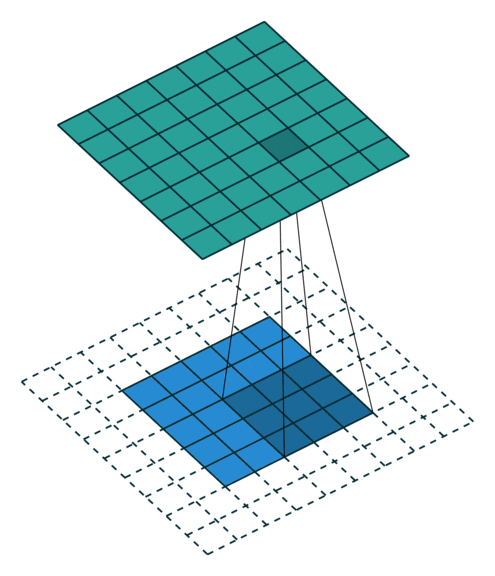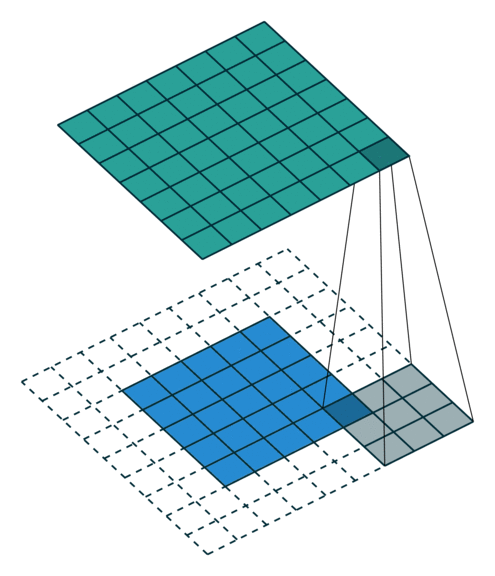
No padding, strides

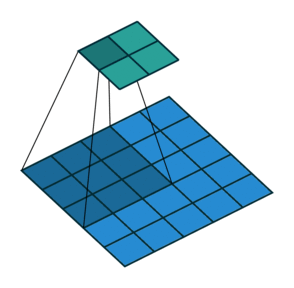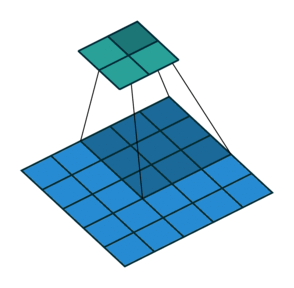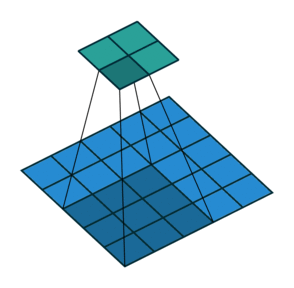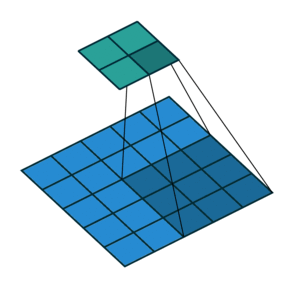
Padding, strides

Pytorch Convolution Operation

• 지금 까지 배운 내용을 Pytorch 함수를 통해 사용하려면 아래 링크를 참조하시면 됩니다.
  • Pytorch Conv2d 함수 다루기