DenseNet (Densely connected convolution networks)

2020, Jun 06    

deep learning 관련 글 목차

• 논문 : https://arxiv.org/pdf/1608.06993.pdf
• 참조 : https://pytorch.org/hub/pytorch_vision_densenet/
• 참조 : https://github.com/pytorch/vision/blob/master/torchvision/models/densenet.py
• 참조 : https://youtu.be/fe2Vn0mwALI?list=WL
• 참조 : https://youtu.be/bhvxLB6Qa60?list=WL

목차

• DenseNet의 성능

• DenseNet 설명

• DenseNet의 효과

• Pre-activation

• Pytorch 코드 설명

DenseNet의 성능

• 이번 글에서는 2017 CVPR에서 소개된 DenseNet에 대하여 다루어 보도록 하겠습니다.
• 먼저 DenseNet은 어떤 효과가 있는 지 다음 그래프를 통하여 간단하게 알아보겠습니다.

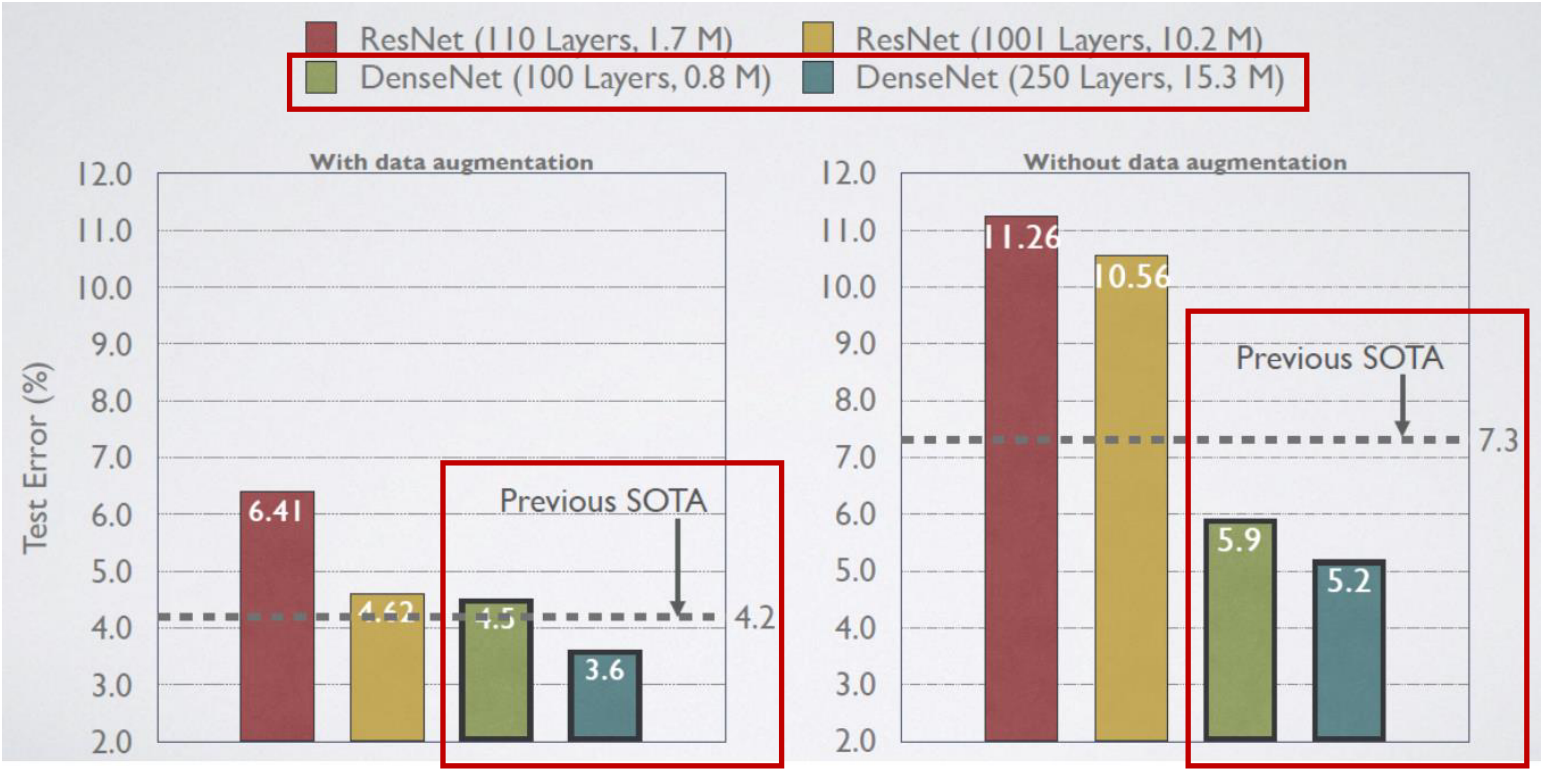
• 먼저 DenseNet의 효과를 살펴보면 강력한 딥러닝 네트워크 중 하나인 ResNet과 비교하였을 때, 더 적은 parameter를 이용하여 더 높은 성능을 내었다는 것에 의의가 있습니다.

DenseNet 설명

• Residual Network를 잘 이해하고 있다면 DenseNet을 이해하기는 상당히 쉽습니다. 만약 ResNet을 잘 모른다면 앞에 연결해 놓은 링크를 통해 먼저 학습을 하고 이 글을 읽기를 권장드립니다.
• DenseNet은 ResNet과 많이 닮았습니다. 즉, 네트워크의 성능을 올리기 위한 접근 방식이 비슷하다고 말할 수 있습니다.
• 그러면 ResNet이 개발된 배경과 그 이후 DenseNet 까지 차례대로 한번 설명해 보도록 하겠습니다.

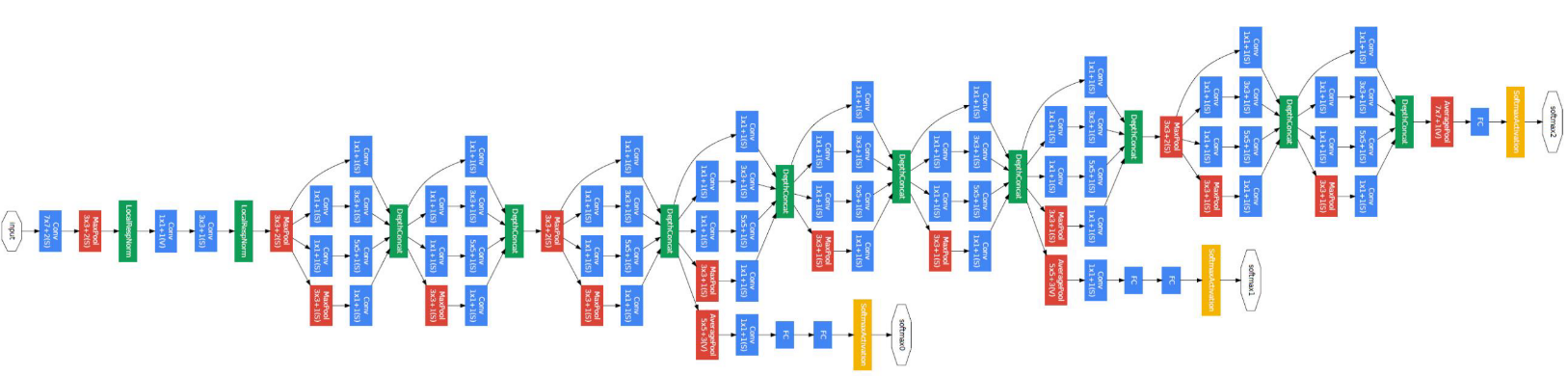
• 위 그림은 GoogLeNet 입니다. 위 네트워크를 보면 그 구조가 다소 복잡하고 깊이가 깊습니다. 이 때부터 복잡하고 깊은 네트워크에서는 학습이 어려워진다는 문제점을 가지고 있었습니다.
• 이 문제를 개선하기 위해 중간 중간에 Auxiliary classifier라는 노란색 부분의 classifier가 존재하여 무조건 끝에서 부터 학습하는 것이 아니라 중간에서도 학습이 가능하도록 만들었습니다.

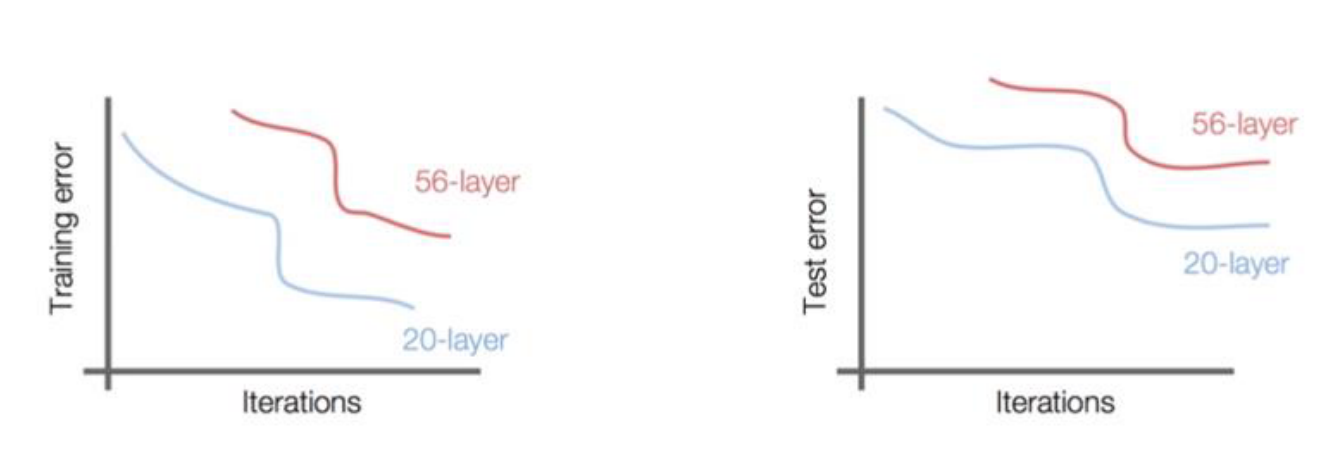
• 이렇게 네트워크의 복잡도가 올라가게 되면 단순히 네트워크를 깊게 쌓는 것이 성능을 높이는 방법이 될 수 없다는 것을 알 수 있었습니다. 위 그래프 처럼 학습을 잘못하게 되면 같은 iteration에서도 성능이 낮음을 알 수 있습니다.

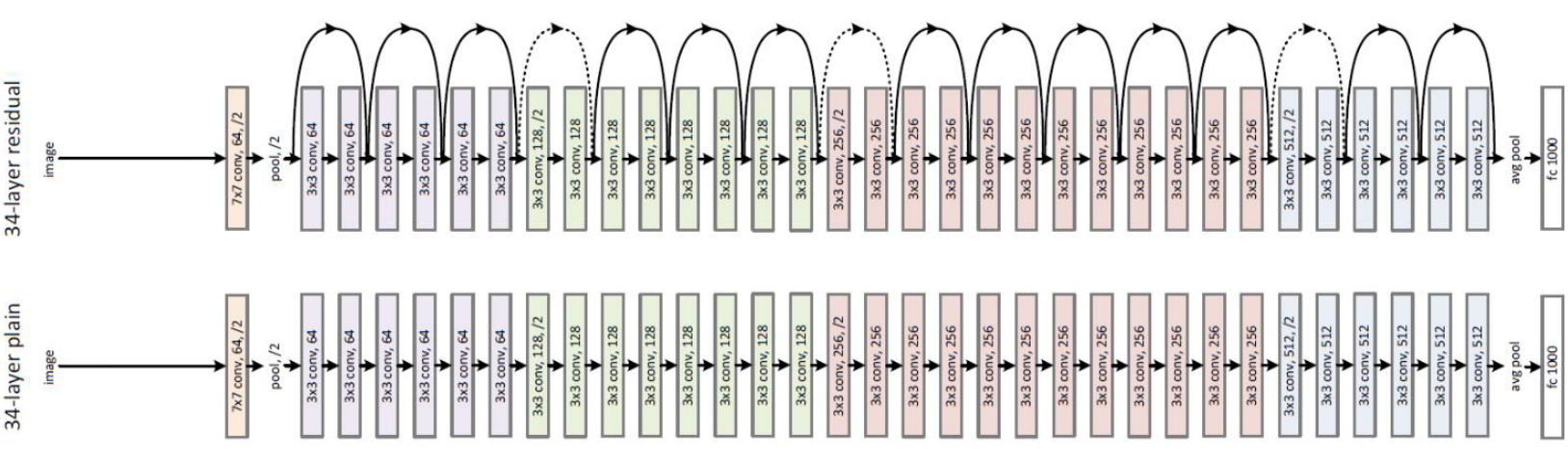
• 여기서 부터가 앞에서 말한 ResNet 입니다. ResNet에서는 중간 중간에 껑충 껑충 뛰는 edge가 output에서 부터 멀리 까지 학습 할 수 있도록 bypass 역할을 함으로써 gradient가 멀리 까지 전파될 수 있도록 합니다.

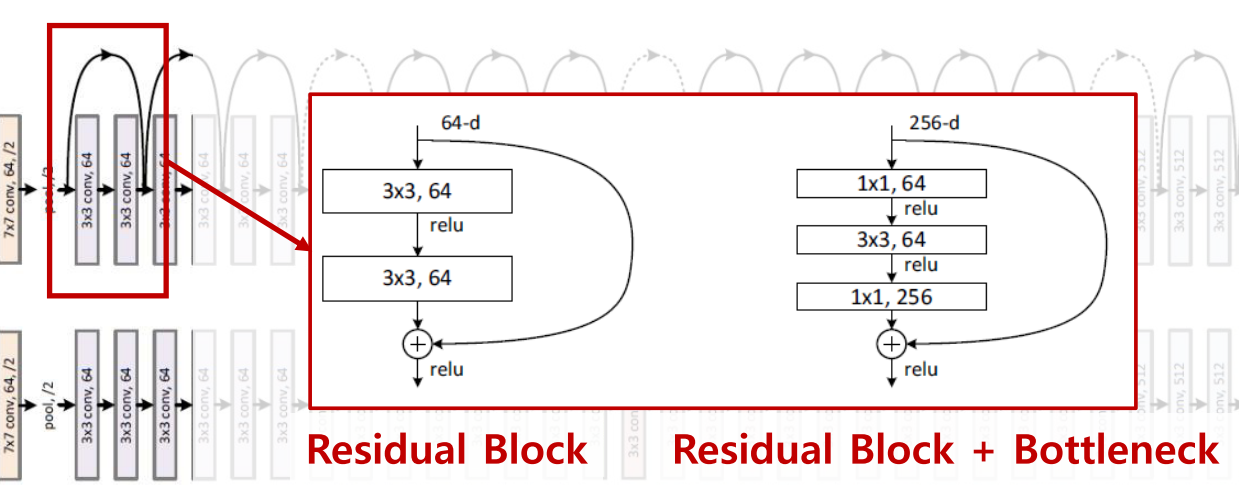
• ResNet의 핵심 부분인 Residual Block을 살펴보겠습니다. 위 그림의 왼쪽이 초기 형태의 Residual Block이고 오른쪽이 Residual Block + Bottleneck 형태입니다.
• Residual Block을 보면 Convolution 연산의 결과(A)와 연산을 거치지 않은 상태(B)를 합하게(A + B) 됩니다. 즉, 이 과정을 통해 Convolution 연산을 거친 것과 거치지 않은 것 모두를 이용하여 학습 시 gradient를 다양한 방식으로 반영할 수 있게됩니다.
• 하지만 단순한 Residual Block에서는 계산량의 문제가 발생하게 됩니다. Residual Block을 계속 쌓게 되다 보니 파라미터가 계속 누적되어 계산량이 증폭되는 문제가 발생하게 됩니다.
• 이 문제를 개선하기 위해 위 그림의 오른쪽 블록인 Residual Block + Bottleneck을 사용하게 됩니다. Bottleneck 구조는 앞에서 살펴 본 GoogLeNet에서 차용한 것입니다.
• Residual Block + Bottleneck에서는 1x1 convolution 연산을 통해 channel reduction을 한 뒤 3x3 convolution 연산을 하고 다시 1x1 convolution 연산을 통해 channel expansion을 하게 됩니다.
• 여기까지가 DenseNet을 설명하기 위한 배경 설명입니다. 그러면 이 ResNet에서 어떻게 DenseNet이 확장되었는지 살펴보겠습니다.

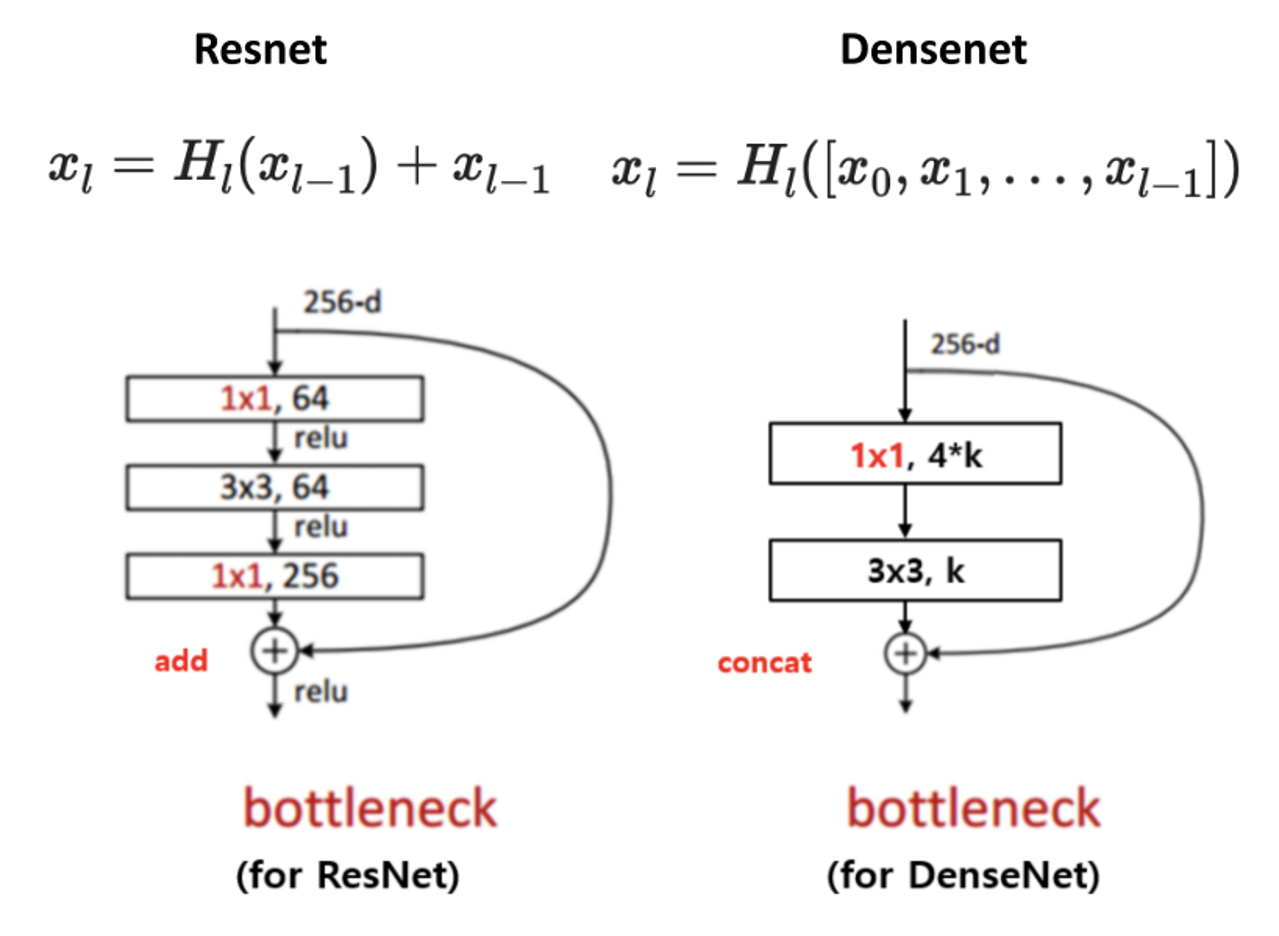
• 먼저 ResNet과 DenseNet의 공통점은 Skip Connection을 이용한다는 점입니다. 즉, 정보를 더 깊은 layer 까지 전달할 수 있는 path를 만들어 학습이 잘 되도록 하였습니다.
• 반면 차이점은 위 그림과 같이 ResNet은 Skip Connection이 덧셈을 통해 이루어지는 반면 DenseNet은 concatenation을 통하여 이루어 집니다. 그 차이점은 수식을 보면 이해할 수 있습니다.
• 먼저 ResNet의 skip connection 부분입니다. 설명한 바와 같이 + 연산을 통해 합쳐집니다.

[x_{l} = H_{l}(x_{l-1}) + x_{l-1}]

• 반면 DenseNet에서는 concatenation을 합니다. 이 방법이 ResNet과의 차이점 입니다.

[x_{l} = H_{l}([x_{0}, x_{1}, \cdots, x_{l-1}])]

• 기존의 ResNet에서는 Bottleneck 구조를 만들기 위하여 1x1 convolution으로 dimension reduction을 한 다음에 다시 1x1 convolution을 이용하여 expansion을 하였습니다. dimension이 축소되었다가 확대되는 구조가 있기 때문에 bottleneck 형상을 만들어 내었다고 생각하면 됩니다.
• 반면 DenseNet에서는 1x1 convolution을 이용하여 dimension reduction을 하지만 expansion은 하지 않습니다. 대신에 feature들의 concatenation을 이용하여 expansion 연산과 같은 효과를 만들어 냅니다.

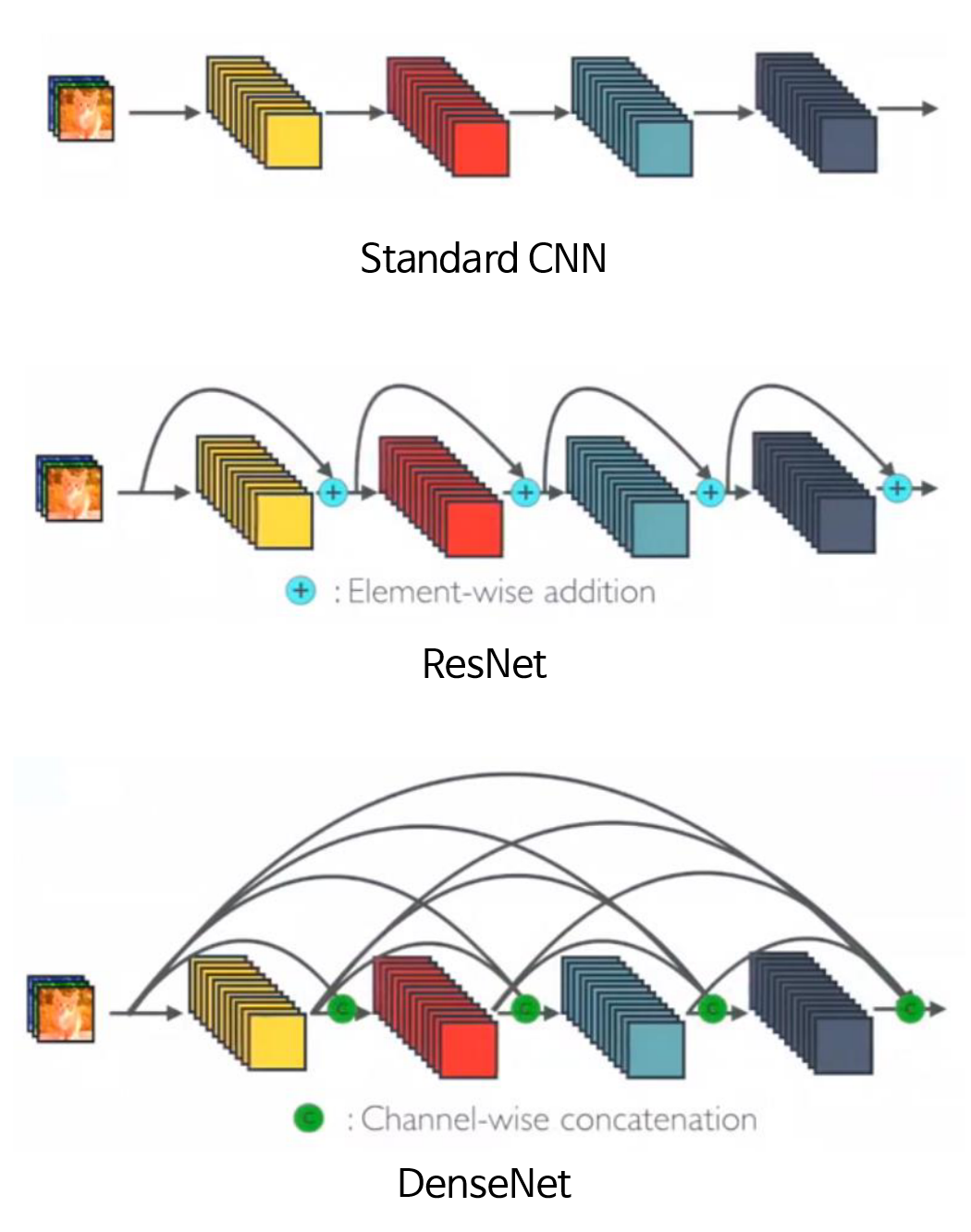
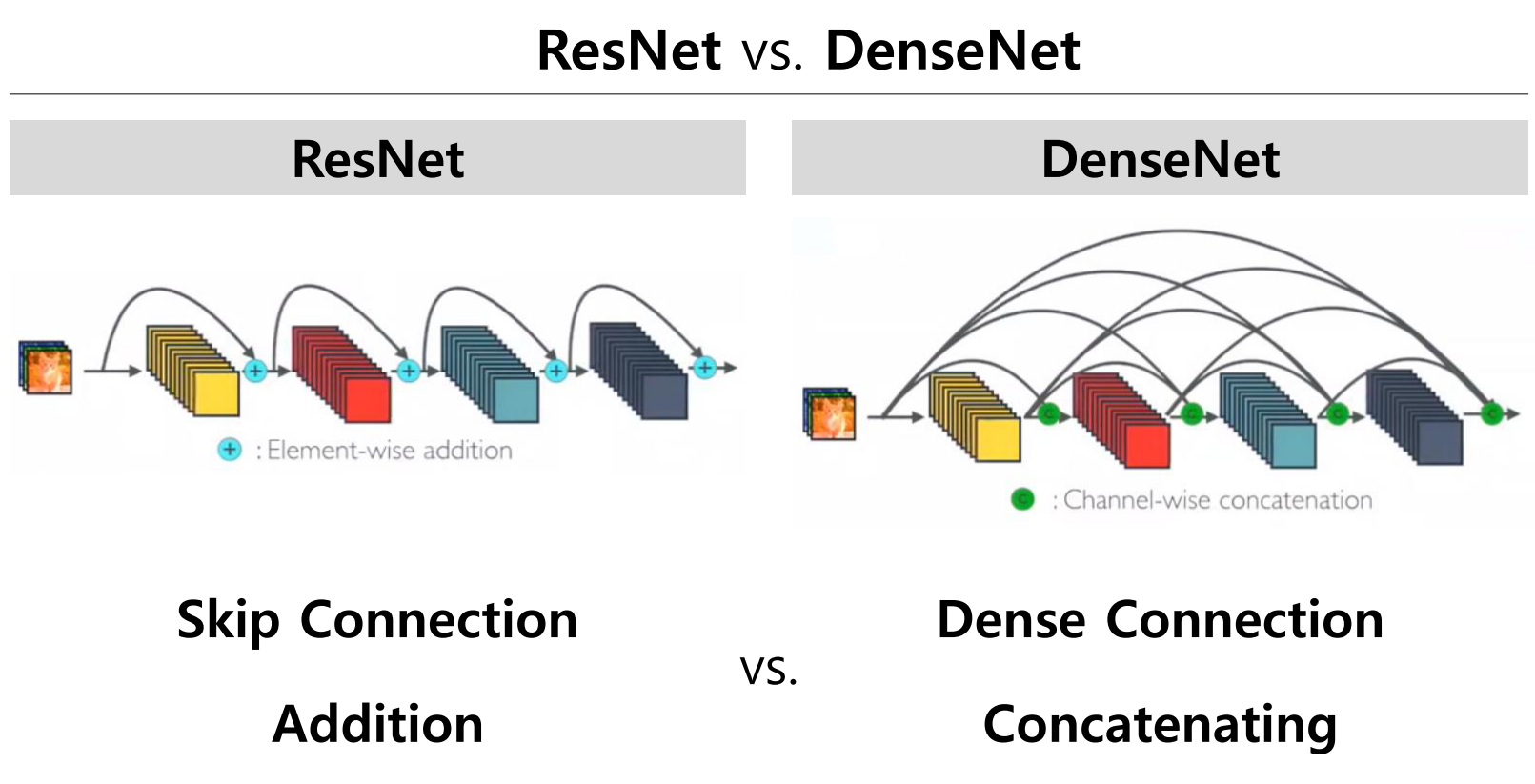
• 기본적인 CNN, ResNet 그리고 DenseNet을 비교 정리하면 위 그림과 같습니다. ResNet은 element-wise addition이고 DenseNet은 channel-wise concatenation임을 이해하면 됩니다.
• 그리고 ResNet은 skip connection을 통하여 바로 뒤의 layer를 연결하는 addition 통로가 생기는 반면 DenseNet은 네트워크 이름과 같이 바로 뒤의 layer 뿐 만 아니라 더 뒤의 layer 까지 연결한 concatenation 통로가 빽빽하게 만들어집니다.

• DenseNet에서 사용되는 개념 중에 얼만큼 feature가 늘어날 지에 대한 값을 하이퍼 파라미터로 가지게 되는데 이 값을 growth rate 라고 합니다.
• growth rate를 사용하는 이유는 만약 어떤 layer 이후의 모든 layer들을 전부 concatenation을 하게 된다면 feature의 갯수가 급격하게 늘어나게 됩니다.
• 반면 growth rate 라는 값을 통하여 일정하게 등차수열의 형태로 channel 수가 늘어나게 되면 feature의 갯수가 늘어나는 것을 조절할 수 있습니다.

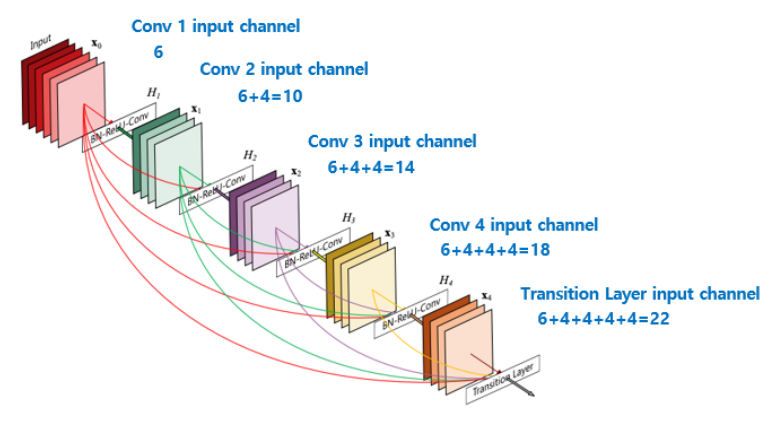
• 위 그림은 DenseNet의 핵심인 dense block을 설명합니다. 5 layer dense block을 나타내며 growth rate는 4입니다. 각각의 layer는 이전의 같은 dense block의 모든 layer의 feature map들을 input으로 받는 것을 볼 수 있습니다.
• growth rate가 4이기 때문에 channel의 수가 등차수열 처럼 4씩 늘어나는 것을 확인할 수 있습니다.

• DenseNet의 전체적인 구조를 살펴보면 위 그림과 같습니다. 위 그림을 보면 Pooling(MaxPooling)을 기준으로 dense block이 구분되어 있음을 확인할 수 있습니다.
• 앞에서 설명한 concatenation은 모든 layer가 아닌 각각의 dense block 내에서 일어납니다.
• dense block의 개념이 DenseNet 전체에서 핵심입니다. 위 아키텍쳐에서 가장 처음에 사용되는 convolution 연산은 input 이미지의 사이즈를 dense block에 맞게 조절하기 위한 용도로 사용되었습니다. 따라서 이미지의 사이즈에 따라서 사용해도 되고 사용하지 않아도 됩니다.

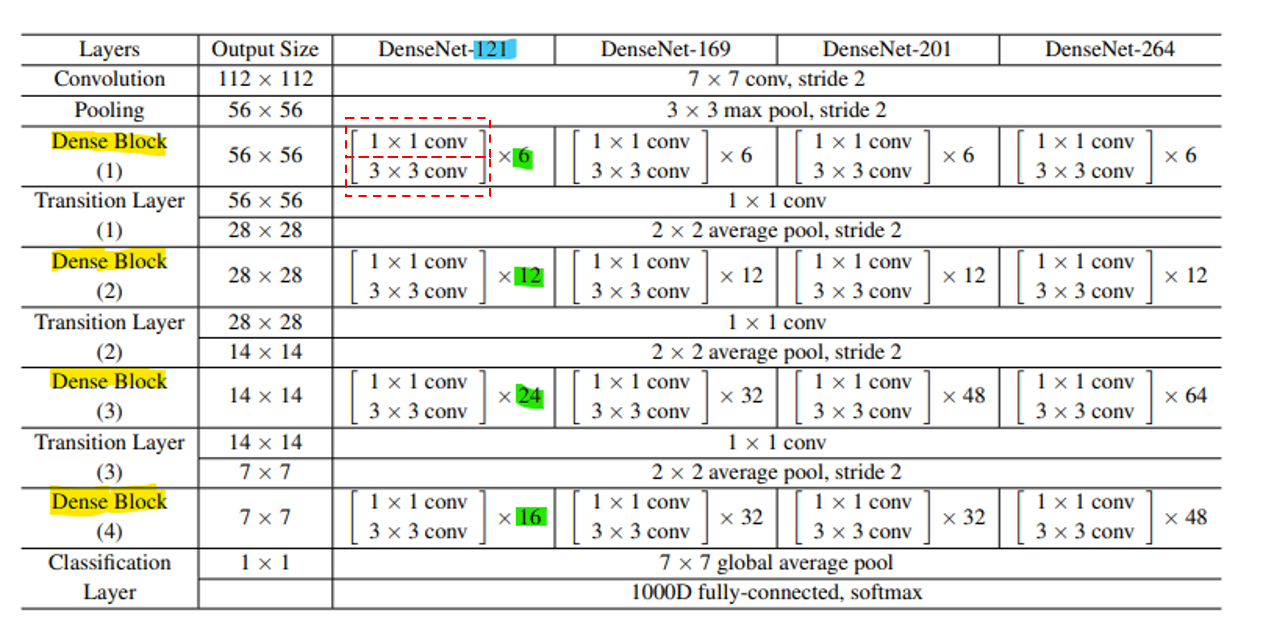
• 위 architecture 설명을 위한 테이블에서 densenet의 핵심 구간은 dense block입니다. 노란색 음영이 있는 행을 유심히 살펴보면 됩니다.
• 각 행의 초록색 음영의 곱해진 숫자는 각 dense block에 존재하는 layer의 갯수를 뜻합니다.
• 그리고 각 dense block의 layer와 나머지 layer 들을 모두 합쳤을 때의 총 layer 갯수가 열에 있는 하늘색 숫자에 해당합니다. 즉, DenseNet-121의 의미는 121개의 layer를 가지고 있는 DenseNet이라고 생각하시면 됩니다.
• 여기까지가 기본적인 DenseNet 입니다.

• 지금부터 설명하는 내용은 DenseNet w/ Bottleneck 이고 DenseNet-B로 표기합니다. 개념은 간단합니다.
• DenseNet 또한 Network를 깊게 쌓다보니 연산 수가 많이 늘어나는 문제가 있습니다. 따라서 GoogLeNet과 ResNet에서 사용하였던 Bottleneck layer를 똑같이 사용하였습니다.
• 위 테이블을 보면 각 Dense Block은 1x1 conv를 거치고 3x3 conv를 거치게 됩니다. 즉, 1x1 conv를 거칠 때, bottleneck 구조를 만들어 연산량을 줄이게 됩니다.
• 논문에서 사용한 1x1 conv와 3x3 conv의 output channel 수는 각각 4k와 k가 되고 k는 앞에서 설명한 growth rate입니다. (4라는 숫자의 해석은 나와있지 않습니다. 실험적으로 발견한 것으로 추측됩니다.)

• 다음은 DenseNet w/ Compression 개념입니다. 이는 DenseNet-C로 표기하겠습니다.
• 이 또한 연산량을 줄이기 위한 방법으로 Dense Block 사이에 1x1 convolution을 이용하여 channel 수를 줄이는 방법입니다.
• 만약 Dense Block의 output의 channel의 수가 \(m\) 이라면 \(\theta m \quad (0 \lt \theta \le 1)\)의 갯수로 줄입니다. \(\theta\)가 1이면 compression을 하지 않은 것입니다.
• 논문에서 사용한 값은 \(\theta = 0.5\)입니다.

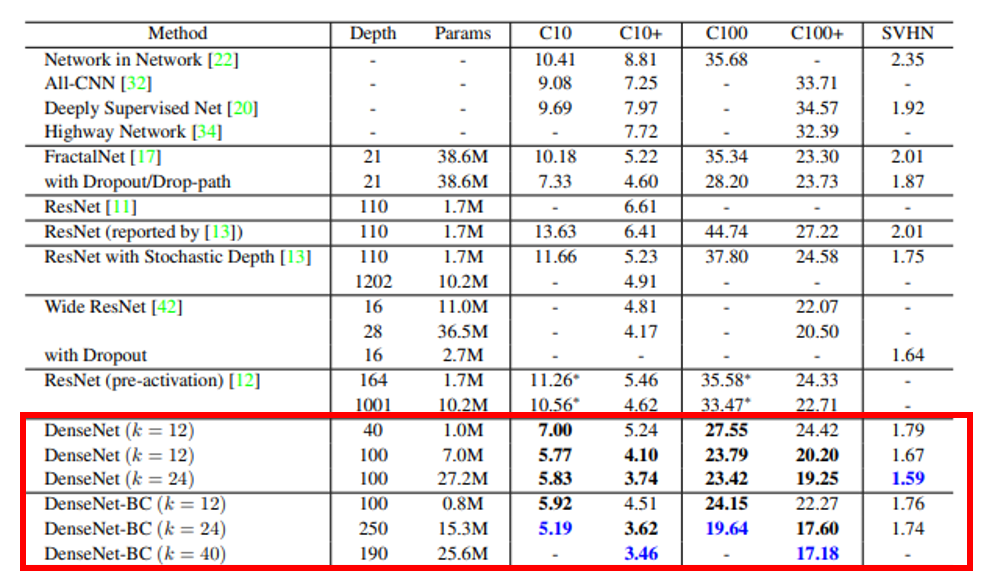
• DenseNet의 성능을 한번 살펴보겠습니다. 위 테이블에서 아래 6개가 이 논문에서 다루고 있는 DenseNet 입니다.
• 그 중 위의 3개는 순수하게 DenseBlock 만을 적용한 DenseNet인 반면 아래 3개는 bottleneck layer와 compression 기법을 동시에 적용한 DenseNet입니다.

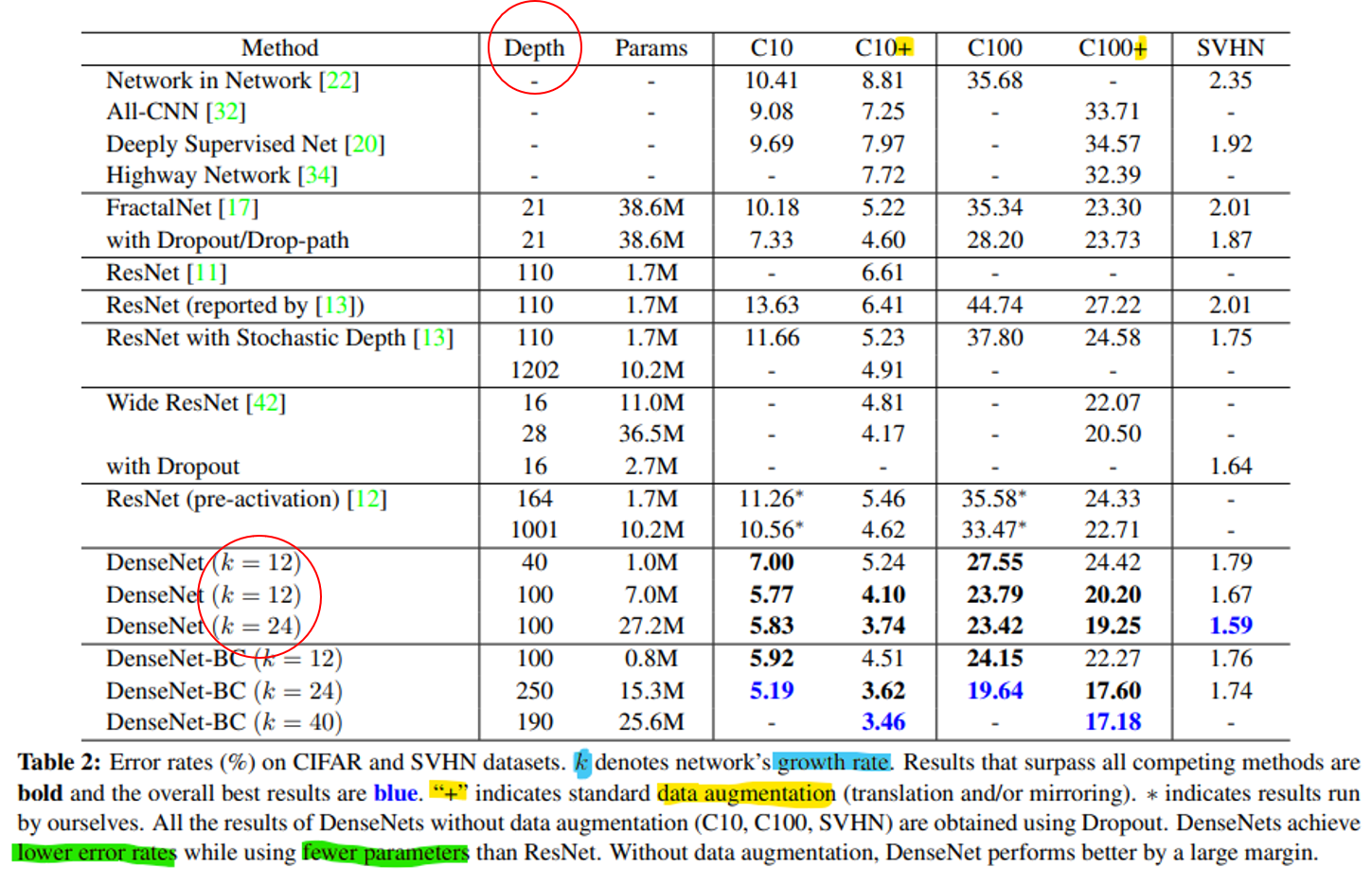
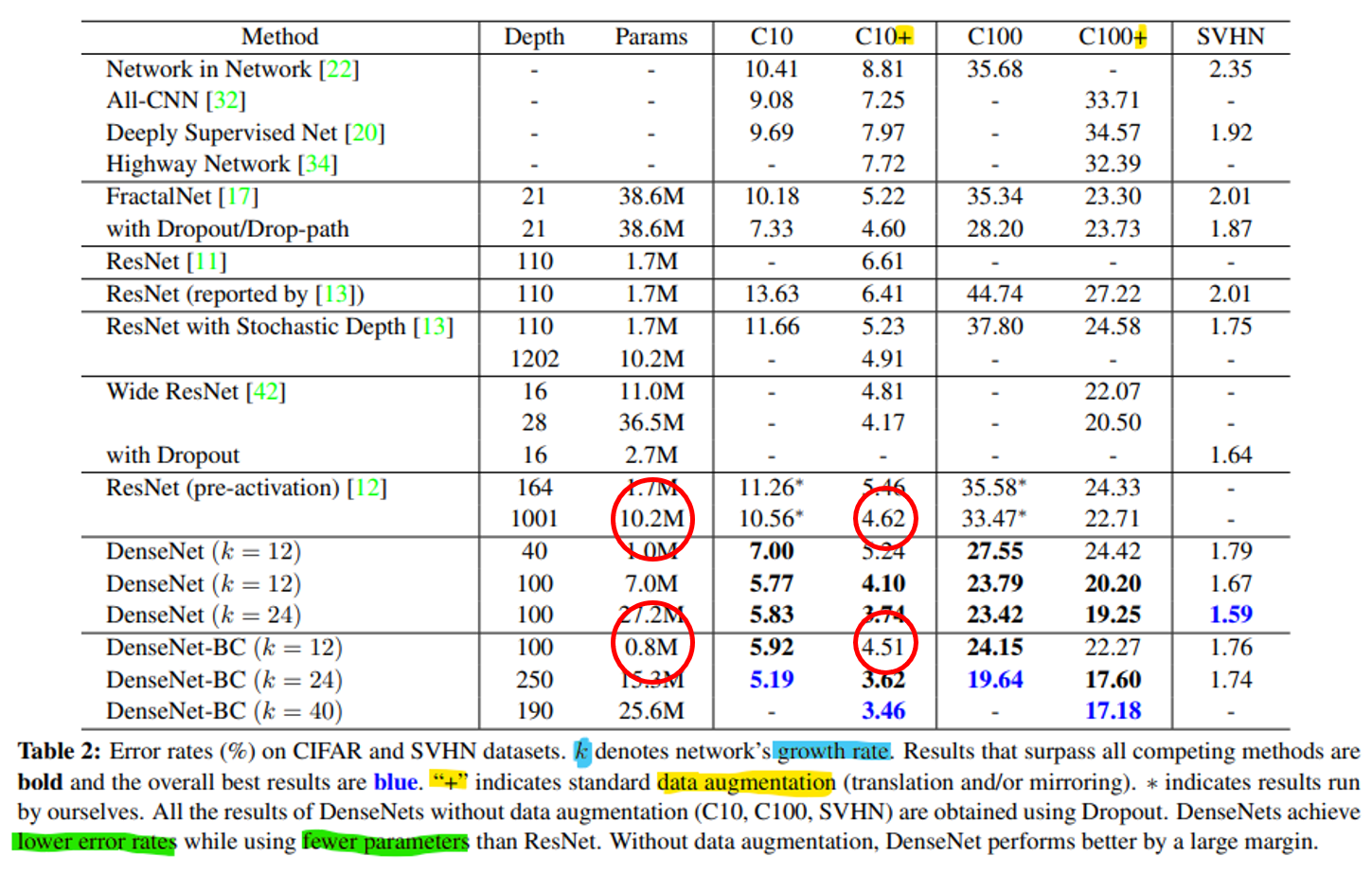
• 먼저 성능을 비교할 때 유심히 볼 곳은 빨간색 원에 해당하는 growth rate인 k와 Depth 입니다. 왜나하면 네트워크의 변화를 줄 수 있는 방법이 바로 growth rate와 depth 이기 때문입니다.
• growth rate와 depth 값 각각은 이 값을 크게 하였을 때, 네트워크의 크기가 더 커지고 파라미터 수도 증가하게 됩니다. 네트워크의 크기가 더 커질수록 성능도 그에 따라 좋아져야 잘 설계된 네트워크라고 말 할 수 있습니다. 반면 오히려 네트워크의 크기가 커지면서 성능이 나빠지는 경우가 생기는 데 이 경우는 네트워크 설계가 잘 못된 것입니다.
• 여기서 growth rate와 depth에 따른 성능의 영향을 살펴 보면 growth rate는 Dense Block의 핵심 하이퍼 파라미터로 propagation을 많이 할 수록 성능이 좋다는 것을 보여줍니다. 그리고 Depth가 깊음에도 불구하고 성능이 좋아야 그만큼 Dense Block이 깊은 layer에서도 학습이 잘된다는 것을 보여줍니다.
• 위 테이블을 보면 growth rate와 depth의 숫자가 클수록 에러도 낮아지는 것을 확인할 수 있습니다. 즉, growth rate와 depth는 성능과 양의 상관관계를 가지므로 DenseNet은 잘 설계된 네트워크라고 말할 수 있습니다.

• 그 다음은 Parameter Efficiency 관점의 DenseNet의 장점입니다.
• DenseNet의 장점 중 하나는 ResNet과 비교하였을 때, 비슷한 성능을 내더라도 그 파라미터의 수가 확실히 작은 것을 볼 수 있습니다.
• 위 빨간색 동그라미를 참조하면 Error rate가 ResNet은 4.62, DenseNet은 4.51로 유사한 수준이지만 파라미터의 수는 10배 이상 ResNet이 많은 것을 확인할 수 있습니다. 즉 그만큼 DenseNet이 효율적인 네트워크라는 뜻입니다.

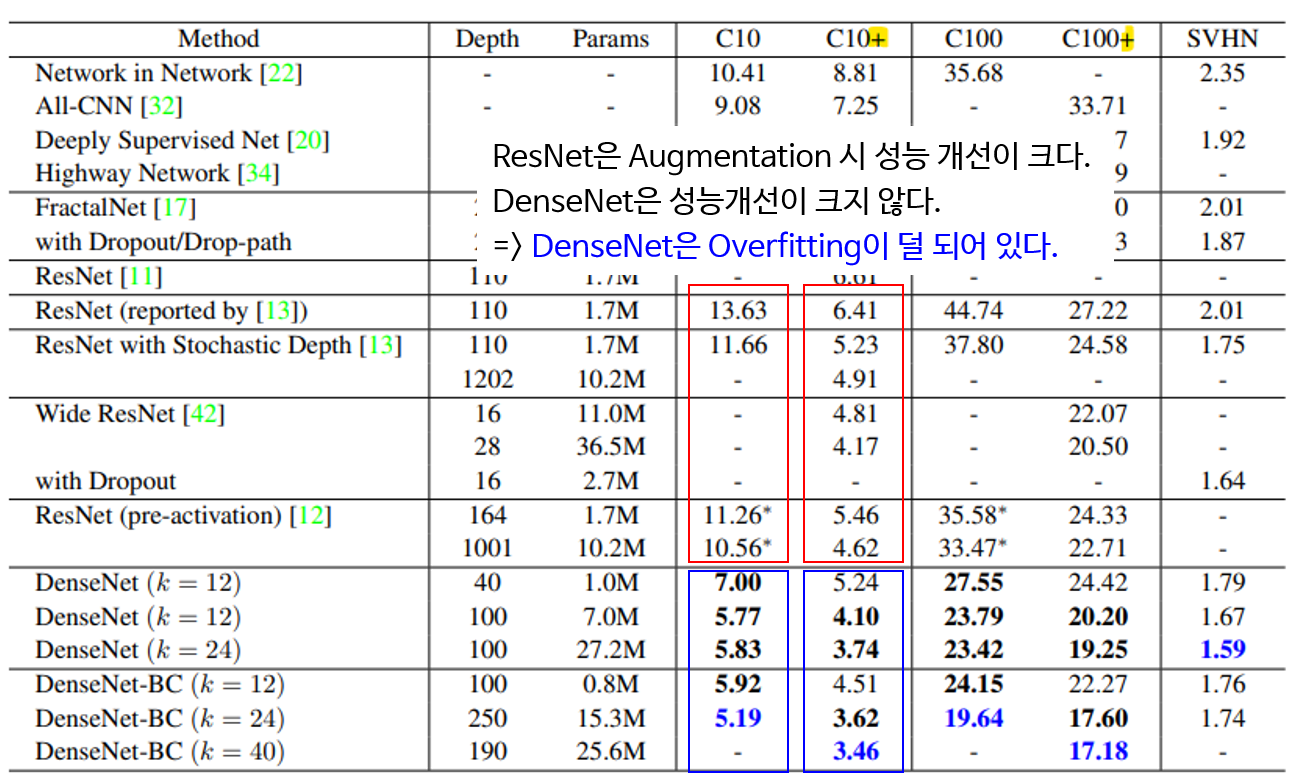
• 그 다음은 Robust in overfitting 관점의 DenseNet의 장점입니다.
• 또한 ResNet은 Data Augmentation 시 성능 개선이 많이 되었지만 DenseNet은 애초에 성능이 좋고 Augmentation에 의한 개선이 ResNet보다는 미미한 것을 볼 수 있습니다.
• 그 이유는 Overfitting에 좀 더 강건하다고 해석할 수 있습니다. 왜냐하면 Data Augmentation이 Overfitting을 개선하기 위한 데이터 증식 기법이기 때문입니다.

DenseNet의 효과

• 앞에서 살펴본 DenseNet이 왜 좋은 효과를 나타내는 지 살펴보도록 하겠습니다. 크게 다음과 같은 4가지 효과가 있습니다.
• 1) vanishing gradient 문제 감소
• 2) feature propagation 강화
• 3) feature 재사용성
• 4) 파라미터의 수 감소

• 먼저 vanishing gradient 문제 감소에 대하여 살펴보겠습니다.

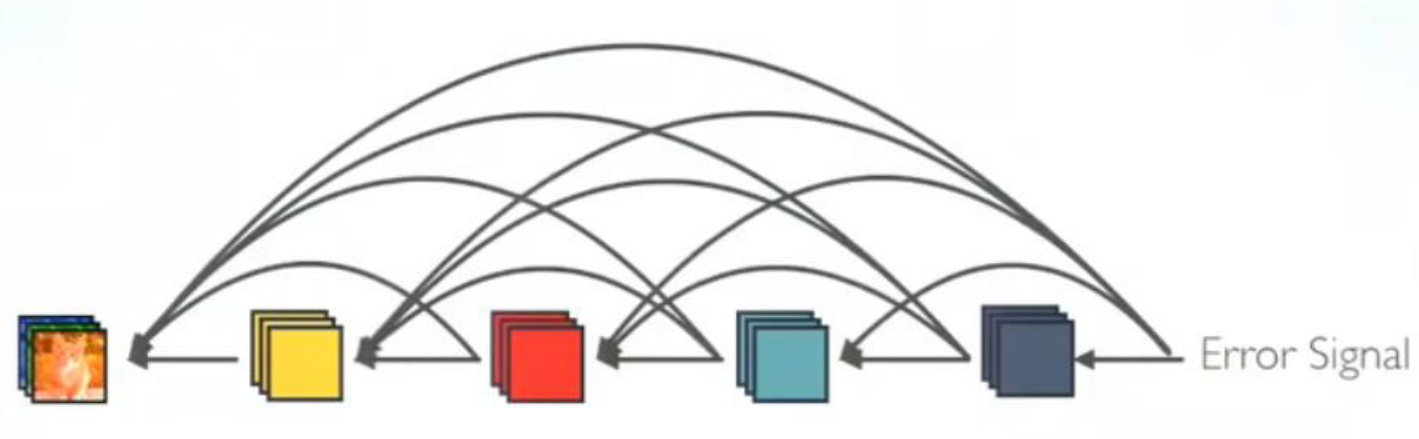
• 위 그림과 같이 DenseNet 또한 ResNet 처럼 gradient를 다양한 경로를 통해서 받을 수 있기 때문에 학습하는 데 도움이 됩니다. 더욱이 ResNet에 비하여 더 멀리 까지 한번에 gradient를 전파할 수 있기 때문에 그 효과가 더 좋다고 해석할 수 있습니다.

• 그 다음으로 feature propagation 강화입니다.

• 위 그림을 보면 앞단에서 만들어진 feature를 그대로 뒤로 전달을 해서 concatenation 하는 방법을 사용을 합니다. 따라서 feature를 계속에서 끝단 까지 전달하는 데 장점이 있습니다.

• 그 다음으로 feature의 재사용성입니다.

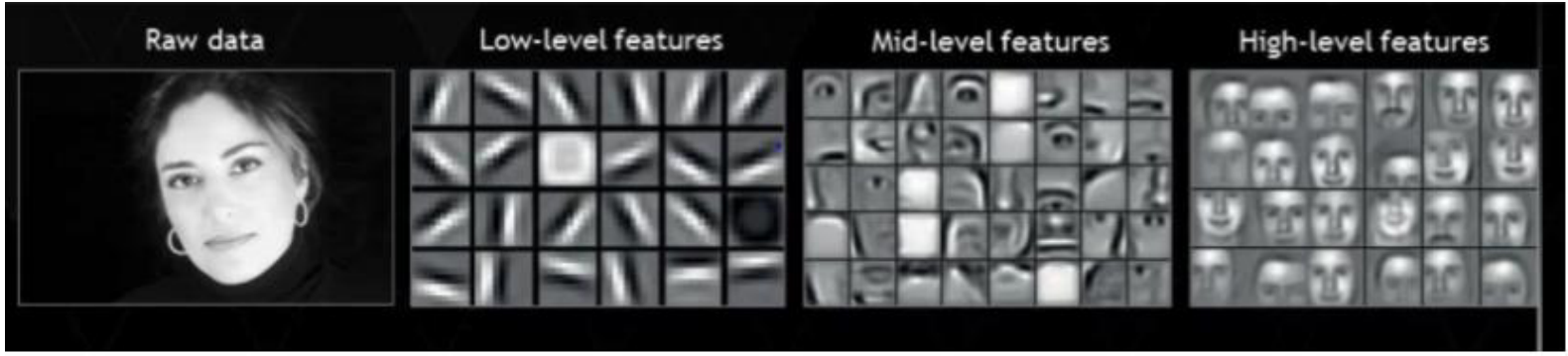
• 딥러닝에서 Input에 가까운 앞쪽 layer에서는 low-level feature를 만들어 내고 Output에 가까운 뒷쪽 layer에서는 high-level feature를 만들어냅니다.
• low-level feature 부터 high-level feature 까지 concatenation을 통해 사용할 수 있도록 만들어 내기 때문에 성능 향상에 도움이 된다고 해석할 수 있습니다.
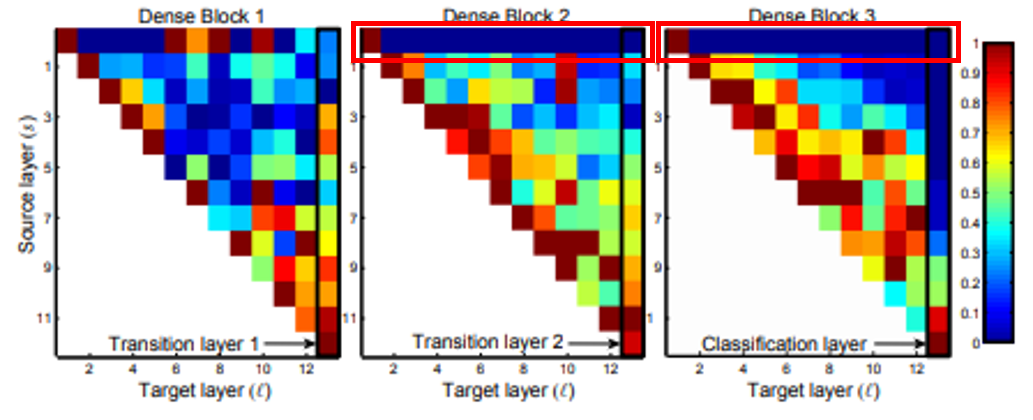
• 특히 DenseNet 논문에서는 각 DenseBlock에서의 feature들이 어떻게 재사용되는 지 그 영향에 대한 분석을 시각화 하여 아래와 같이 표현하였습니다.

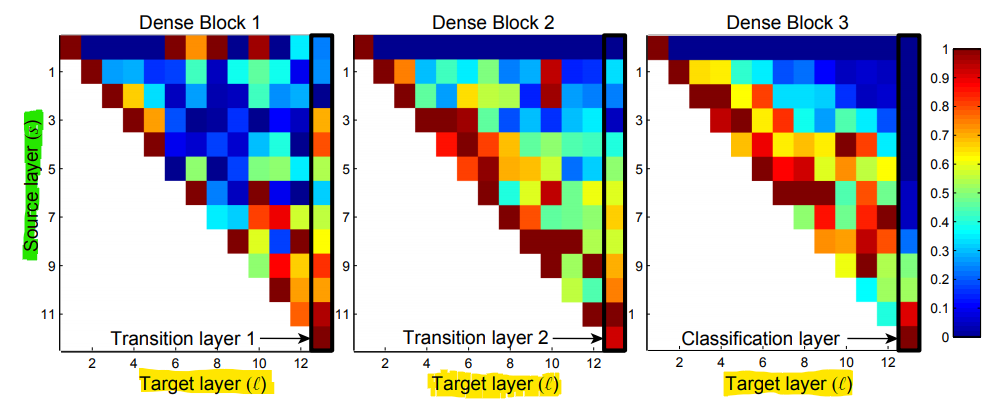
• 위 그림은 각 source → target으로 propagation된 weight의 값 분포입니다.
• 먼저 위 그림의 세로축과 가로축에 대하여 살펴보겠습니다. 위 그림의 세로축은 Source layer 입니다. 즉, layer가 propagation 하였을 때, 그 Source에 해당하는 layer가 몇번째 layer인 지 나타냅니다.
• 반면 가로축은 Target layer입니다. 즉, Source에서 부터 전파된 layer의 목적지가 어디인지 나타냅니다.
• 예를 들어 DenseBlock1의 세로축(5), 가로축 (8)에 교차하는 작은 사각형이 의미하는 것은 DenseBlock1에서 5번째 layer에서 시작하여 8번째 layer로 propagation 된 weight라고 보시면 됩니다.

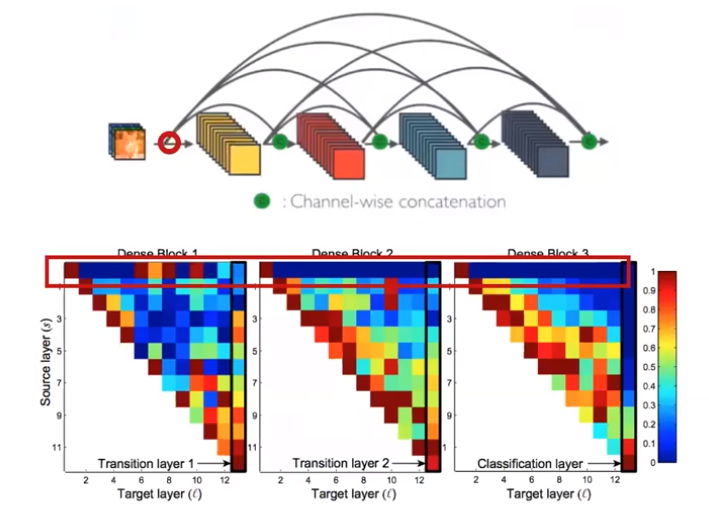
• 예를 들어 각 DenseBlock의 Source는 1인 부분들을 살펴 보면 각 Block의 첫 layer에서 펼쳐진 propagation에 해당합니다. 위 네트워크 아키텍쳐 그림에서 빨간색 동그라미에 해당하는 부분이라고 보시면 됩니다.

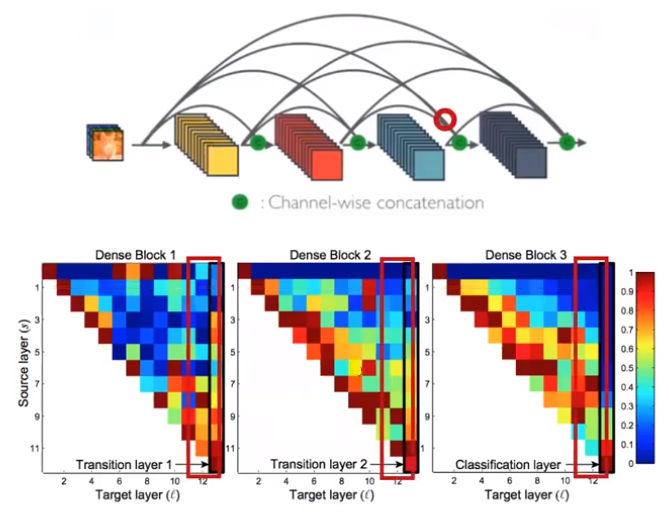
• 이번에는 관점을 바꾸어 각 DenseBlock의 Target이 12인 부분들을 살펴 보면 다양한 Source에서 weight들이 모이게 된 것을 확인하실 수 있습니다. 위 네트워크 아케틱쳐 그림에서 빨간색 동그라미에 해당하는 부분이라고 보시면 됩니다.

• 그 다음으로 각 사각형의 색깔에 대하여 살펴보겠습니다.
• 각 사각형의 색깔은 각 DenseBlock의 weight들이 가지는 그 크기 값을 0 ~ 1 사이 범위로 normalization 한 결과입니다.
• 빨간색인 1에 가까울 수록 큰 값을 가지고 파란색인 0에 가까울수록 그 값이 작다고 생각하시면 됩니다.

• 마지막으로 파라미터의 수 감소입니다.

• DenseNet에서는 앞에서 설명한 growth rate를 통하여 channel의 증감량을 조절하고 있습니다. 따라서 이 growth rate를 작게 잡으면 feature를 계속 channel 방향으로 쌓아가더라도 늘어나는 파라미터의 갯수는 많지 않다는 것입니다.
• 위 그림 예제에서는 growth rate는 3입니다. 왜냐하면 layer가 깊어질수록 3개의 channel만 등차적으로 늘어나기 때문입니다.
• 논문에서 주로 사용하는 growth rate는 12입니다. 즉 각 convolution layer를 거칠 때 마다 12개의 채널이 증가됩니다. 이를 다른 CNN 모델과 비교해 보면 상대적으로 작은 증가량임을 알 수 있습니다.

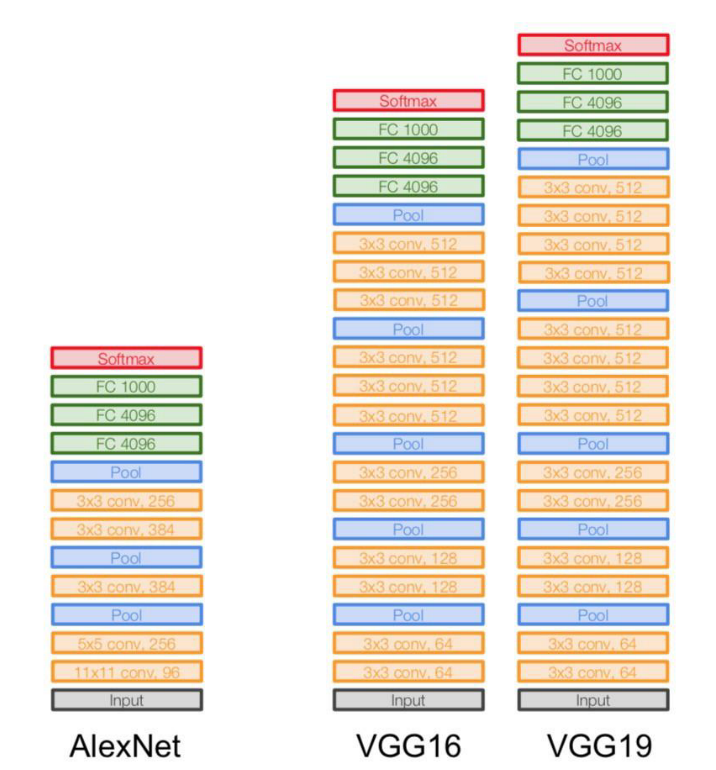
• 예를 들어 위의 AlexNet과 VGG를 보면 각 layer의 마지막에 적힌 숫자(e.g. 64, 128, 256, …)가 channel 수입니다. VGG에서는 대략 2배씩 늘어나는 것에 비하면 growth rate를 통해 등차로 늘어나는 것은 상대적으로 적은 파라미터의 증가라고 해석할 수 있습니다.

Pre-activation

deep learning 관련 글 목차