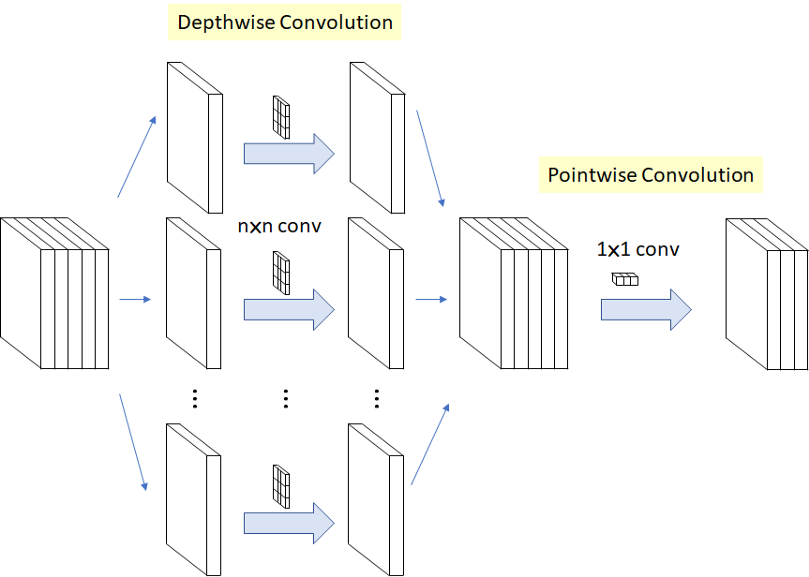
Depthwise separable convolution 연산

이번 글에서는 convolution 연산 방법 중 하나인 depthwise separable convolution에 내용에 다루어 보도록 하겠습니다.
제 블로그의 mobilenet 관련 글을 참조하셔도 좋습니다.

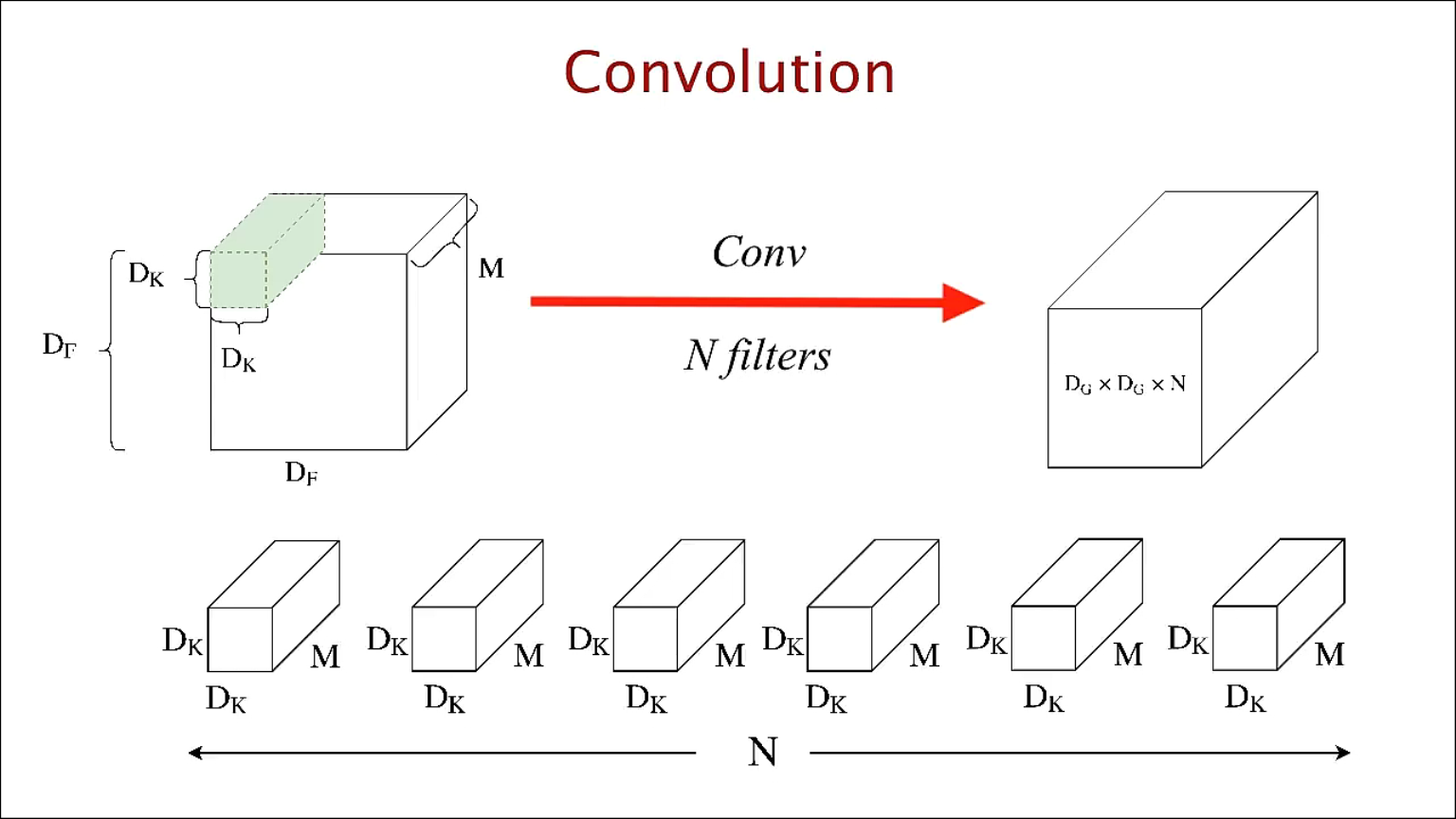
위 슬라이드는 일반적인 convolution 연산을 나타냅니다.
살펴보면 $D_{F}$ 는 height와 width의 크기이고 $M$ 은 채널의 크기입니다. 인풋이 컬러 이미지라면 $M$ 은 R,G,B로 3입니다.
- 따라서 인풋의 shape은 $(D_{F}, D_{F}, M)$ 이 됩니다.
그리고 $D_{K}$ 는 필터(커널)에 해당합니다. 필터의 채널은 인풋의 채널과 같기 때문에 똑같이 $M$ 이 됩니다.
인풋이 필터를 거쳐 convolution 연산을 하게 되면 결과물로 매트릭스가 한 개 나오게 됩니다. (채널이 1인 텐서인 형태입니다.)

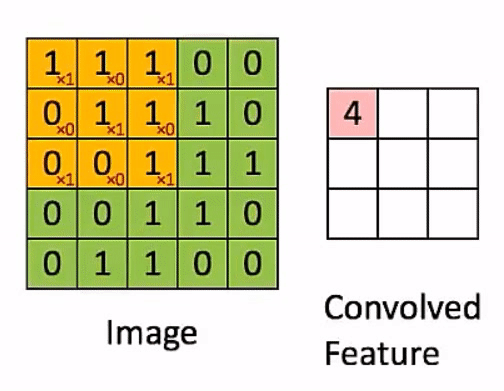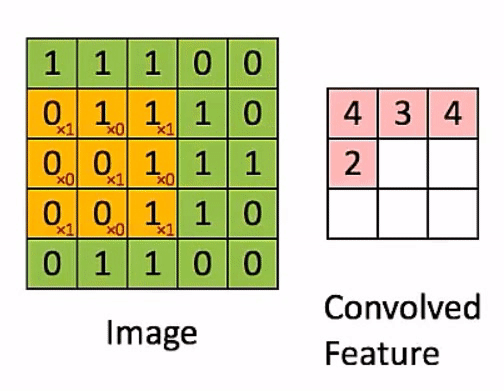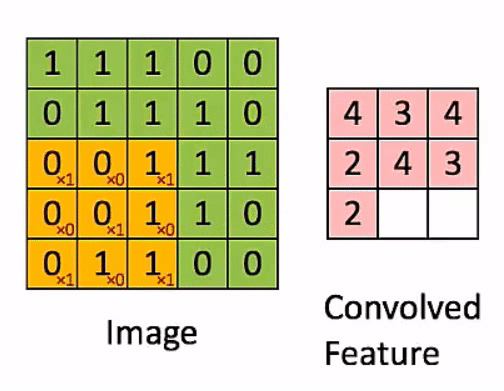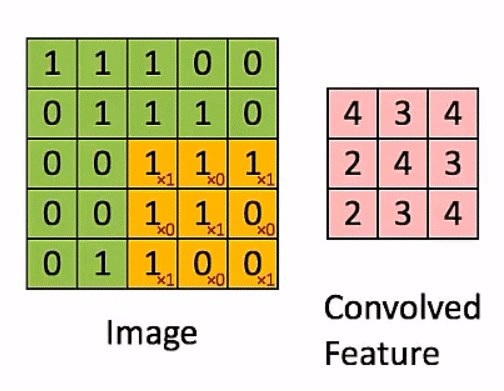
그 다음 필터의 갯수가 $N$ 에 해당하는데 필터의 종류(N개) 만큼 convolution 연산을 하기 때문에 총 $N$ 개의 매트릭스가 결과물로 나오게 됩니다.
이것들을 모두 쌓으면 출력단에 $(D_{G}, D_{G}, N)$ shape의 volume이 출력물로 나오게 됩니다.

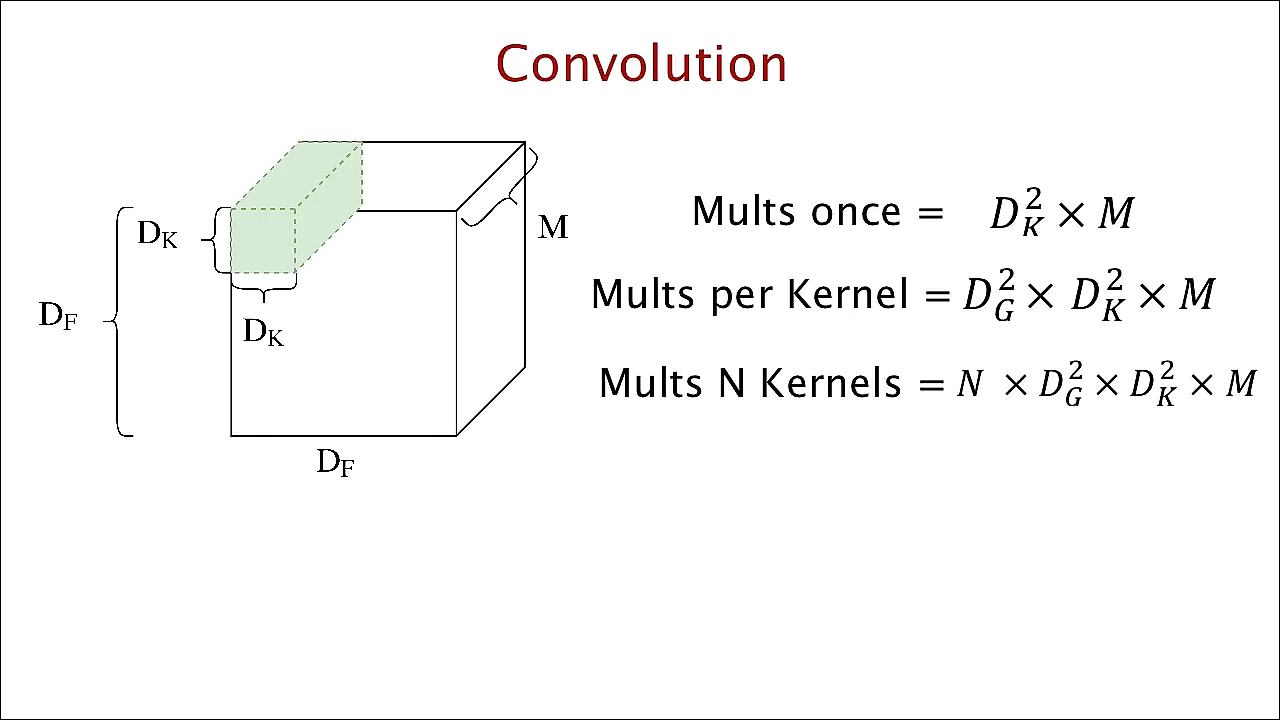
그러면 이 연산의 연산량이 얼마가 되는지 간략하게 알아보겠습니다. 연산량을 간단하게 알아보기 위해 곱연산을 기준으로 알아보겠습니다.
먼저 한 개의 필터가 인풋의 한 위치에서 처리할 때 사용되는 곱연산은 $D_{K}^{2} \times M$ 이 됩니다.
이 때, 이동할 수 있는 위치의 경우의 수가 $D_{G} \times D_{G}$ 의 경우가 있기 때문에( $D_{G}$ 는 아웃풋의 height, wdith 크기) 필터 하나가 인풋 하나를 처리하는 데 필요한 연산 수는 $D_{G}^{2} \times D_{K}^{2} \times M$ 이 됩니다.
마지막으로 $N$ 개의 필터가 있다면 아웃풋은 $(D_{G}, D_{G}, N )$ 크기를 가지고 연산량도 $N \times D_{G}^{2} \times D_{K}^{2} \times M$ 가 됩니다.
depthwise separable convolution은 $N \times D_{G}^{2} \times D_{K}^{2} \times M$ 연산량을 줄이는 것이 목표입니다.

depthwise separable convolution은 두가지 과정을 거칩니다.
- depthwise convolution: filtering stage
- pointwise convolution: combination stage

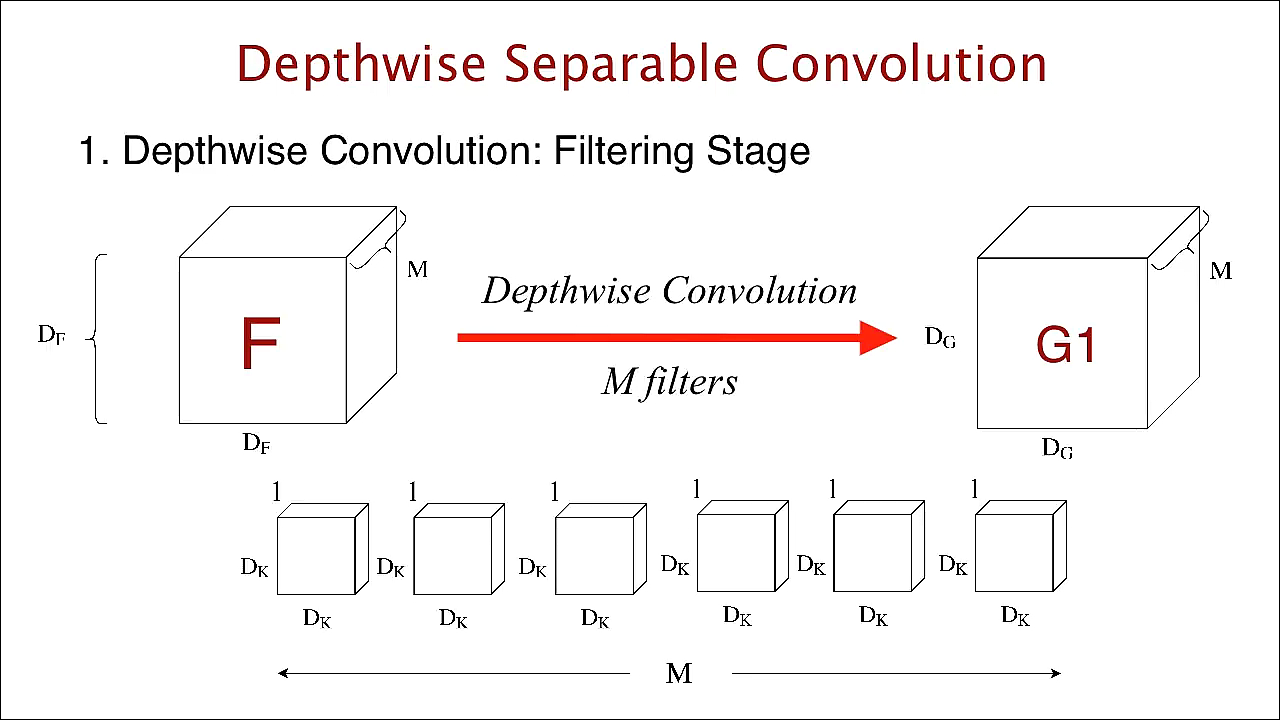
먼저 depthwise convolution 부터 알아보겠습니다.
standard convolution 연산에서는 한 개의 필터가 $M$ 채널 전체에 convolution 연산을 하였습니다.
반면 여기서는 한 개의 필터가 한 개의 채널에만 연산을 합니다. 즉, 인풋의 첫번째 채널에 해당하는 영역을 $(D_{F}, D_{F}, M_{1})$ 이라고 한다면 이 1채널 인풋과 유일하게 연산되는 필터 $(D_{k}, D_{k}, 1)$ 이 존재합니다.
그러면 $(D_{F}, D_{F}, M_{i})$ 는 $(D_{K}, D_{K}, M_{i})$ 와 대응되므로 이 연산에서는 총 $M$ 개의 필터가 존재하게 됩니다.
연산을 마치면 최종적으로 $(D_{G}, D_{G}, M)$ 의 volume이 출력됩니다.

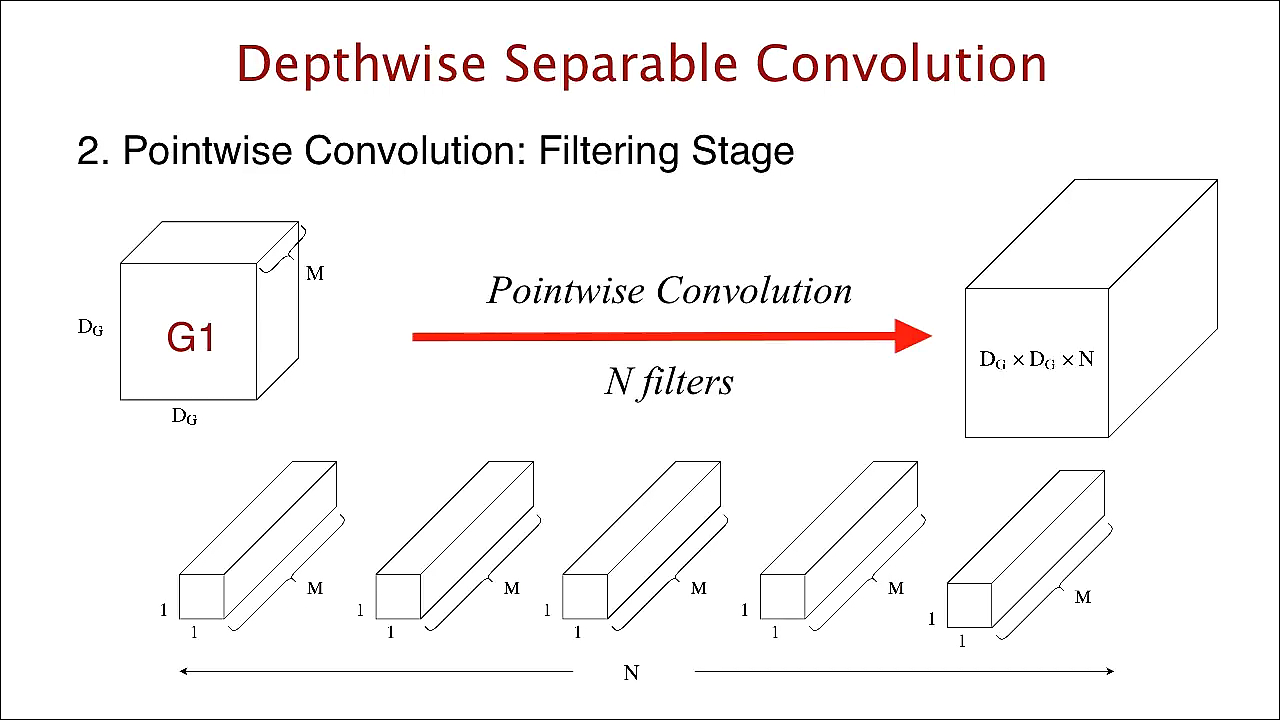
이 다음 연산은 pointwise convolution 입니다.
depthwise convolution 연산을 마치면 출력이 $(D_{G}, D_{G}, M)$ 이었습니다.
여기서 1 x 1 convolution을 적용하는 것이 이번 연산의 핵심입니다. $(D_{G}, D_{G}, M)$ 에 $(1, 1, M)$ 필터를 convolution 연산을 취해줍니다.
그러면 $(D_{G}, D_{G}, M) \otimes (1, 1, M) = (D_{G}, D_{G}, 1)$ 이 됩니다. 이 연산을 $N$ 개의 $(1, 1, M)$ 필터를 이용하여 적용하면 총 $N$ 개의 매트릭스( $(D_{G}, D_{G}, 1)$ 가 $N$ 개)가 출력 됩니다.
이 출력물들을 stack 하면 결과적으로 $(D_{G}, D_{G}, N)$ 의 출력물을 만들 수 있습니다.

입력과 출력 기준으로 보면 standard convolution과 depthwise separable convolution 모두 $(D_{F}, D_{F}, M)$ 을 입력으로 넣어서 $(D_{G}, D_{G}, N)$ 의 출력을 얻는다는 점은 같습니다.
다만 내부 convolution 연산 과정에서 depthwise separable 기법으로 2단계로 나누어 좀 더 연산량과 파라미터 수를 줄였다는 것이 핵심입니다.
그러면 얼마나 연산량이 줄었는지 살펴보겠습니다.

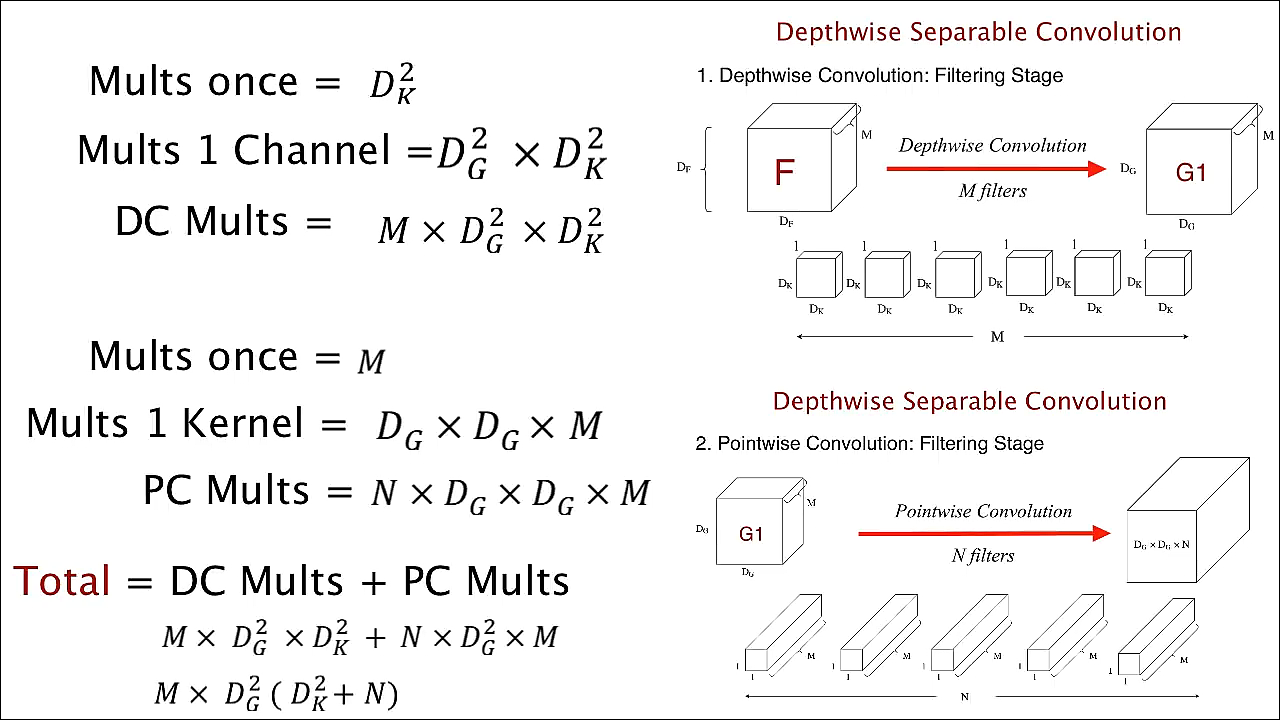
첫번째로 depthwise convolution의 연산량입니다.
한 위치에서 필터가 연산되는 곱연산은 $D_{K}^{2}$ 이고 한 채널 전체에서 필터가 연산되는 곱연산은 $D_{G}^{2} \times D_{K}^{2}$ 입니다.
마지막으로 $M$ 개의 채널에 모두 적용되어야 하므로 총 곱연산은 $M \times D_{G}^{2} \times D_{K}^{2}$ 가 됩니다.
두번쨰로 pointwise convolution의 연산량입니다.
한 위치에서 1x1 필터가 연산되는 곱 연산은 $M$ 입니다. 그리고 한 채널 전체에서 연산되는 곱연산은 $D_{G}^{2} \times M$ 이 됩니다.
마지막으로 $N$ 개의 필터가 모두 적용되어야 하므로 총 곱연산은 $N \times D_{G}^{2} \times M$ 이 됩니다.

그러면 얼마나 연산량이 줄었나 확인해보도록 하겠습니다.
standard convolution의 연산량은 $N \times D_{G}^{2} \times D_{K}^{2} \times M$ 이고 depthwise separable convolution의 연산량은 $M \times D_{G}^{2}(D_{K}^{2} + N)$ 이 됩니다.
위 슬라이드와 같이 비율을 확인해 보면 $(1 / N) + (1 / D_{K}^{2})$ 이 됩니다.
$N$ 은 아웃풋 채널의 수이고 $K$ 는 필터의 사이즈이므로 일반적인 예를 들어 $N = 1024, K = 3$ 이라고 하면 $(1/1024) + (1/9) = 0.112..$ 가 됩니다.
즉, 필터의 사이즈에 가장 큰 영향을 받게 되고 필터의 크기는 3을 사용하므로 약 $1/9$ 만큼 연산량이 줄어든것을 확인할 수 있습니다.

다시 정리하면 위와 같습니다.
개념에 대해서는 다 배웠습니다! 이 연산 기법은 Xecption, Mobilenet V1, V2에 현재 활발히 사용되고 있으니 정확히 공부해 놓는것이 좋을 것 같습니다.