
gram matrix used in style transer
- 아래는 영어로 작성(?)해 봤던
gram matrix 입니다.
Today, we are going to study about gram matrix used in Style transfer.
What is the gram matrix?
Let \(\vec{x}\) be a flatten image vector. (even though in this example it has only 3 elements for simplicity.)
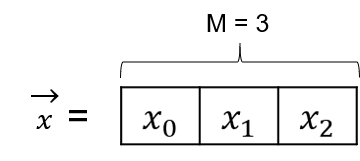
The shape of image is not important because we will flatten matrix/tensor to vector as pre-processing.
Accordingly, principle of applying gram matrix is same with following method.
Let \(Z_{0}, Z_{1}\) be filters applying to vector \(\vec{x}\).
In order to make gram matrix, we will follow below procedure.
Apply \(\vec{x}\) to \(Z_{0}, Z_{1}\).
In below example, N = #filters = 2 & M = #pixel = 3.

Calculate gram matrix
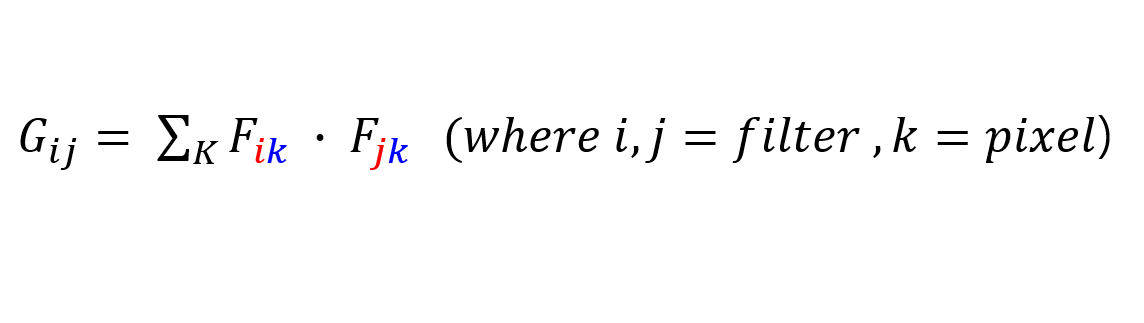
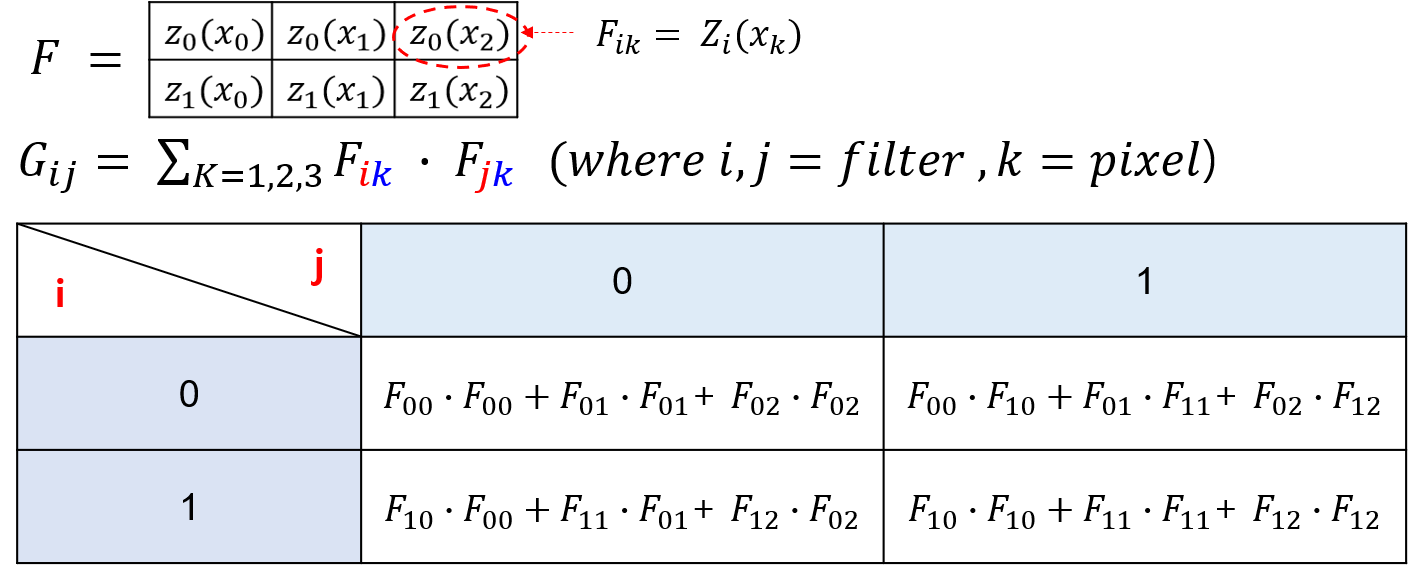
gram matrix means the relation between filters.
It looks similar with correlation.
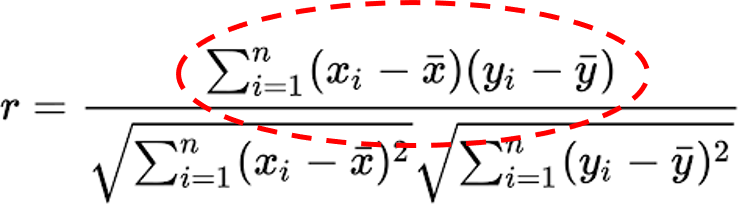
The difference between gram matrix and correlation is whether to subtract mean before multiplying.
(In gram matrix there is no subtraction.)
But, like a correlation, gram matrix also means the relation between two distributions(filters).
Okay! This concept is very important to understand the Neural Style Transfer.
Thanks for reading.