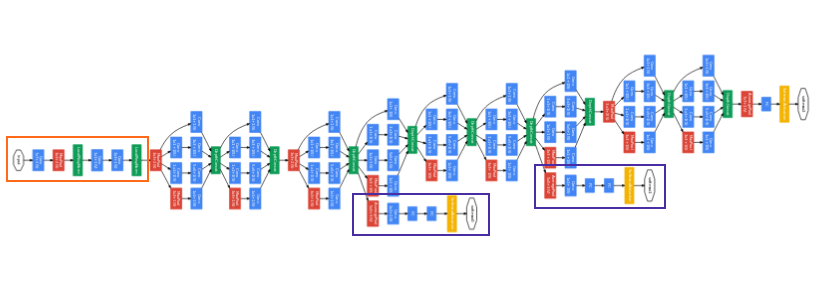
Inception Module과 GoogLeNet

참조 :
- https://youtu.be/V0dLhyg5_Dw
- https://m.blog.naver.com/laonple/220808903260
이번 글에서는 GoogLeNet 또는 Inception이라는 딥 뉴럴 네트워크에 대하여 알아보도록 하겠습니다.

Inception motivation

딥 뉴럴 네트워크는 깊고 넓은 네트워크가 성능에 더 좋다 라는 관점이 있었으나 그것에 대한 단점들을 해결하는 과정에서 나온 아이디어들을 적용하였습니다.
단순히 깊고 넓은 네트워크는 학습시키는 데 오래 걸린다는 단점이 있었습니다. (연산량과 파라미터가 너무 많기 때문이지요)
먼저 파라미터의 수를 줄이는 방법은 1x1 convolution과 Tensor factorization을 이용하여 그 수를 줄일 수 있었습니다.
- 먼저 1x1 convolution을 이용하면 width, height의 크기는 유지하되 채널의 수만 줄일 수 있기 때문에 채널의 수를 줄였다가 다시 늘리는 방법으로 파라미터의 수를 줄일 수 있습니다.
- 다음으로 Tensor factorization은 행렬을 곱하기 전 상태의 파라미터를 저장함으로써 행렬의 곱 이후에 늘어나는 파라미터의 갯수에 대비하여 파라미터 수를 적게 저장하는 방법입니다. 비유를 하면 다음과 같습니다.
\[\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \begin{bmatrix} 4 & 5 & 6 \end{bmatrix} = \begin{bmatrix} 4 & 5 & 6 \\ 8& 10 & 12 \\ 12 & 15 & 18 \end{bmatrix}\]
- 위 식을 보면 계산하기 전에는 파라미터가 6개였지만 계산 후에는 파라미터가 총 9개로 늘어났습니다. 이렇게 matrix 곱을 factorizaion 하였을 때 파라미터의 수가 줄어드는 경향이 있기 때문에 이 방식을(Tensor factorization) 이용하여 파라미터를 줄일 수 있었습니다.
- 자세한 내용은 이 글의 뒷부분에서 다루어 보겠습니다.
그 다음으로 연산을 효율적으로 하는 방법은 matrix 연산을 dense 하게 해야합니다.
- CNN 계열에서 가장 많은 연산이 필요한 것은 convolution filter(kernel)을 stride 만큼 옮겨가면서 feature와의 convolution 연산 (matrix의 dot product 연산)을 하는 것인데 이런 matrix 연산을 할 때, GPU의 성능을 최대화 하려면 matrix 자체가 dense 해야 한다는 것입니다. (즉, matrix에 0이 많지 않고 유효한 숫자가 많아야 한다는 뜻입니다.)

조금 전에 다루어 본 것은 파라미터의 수와 연산의 효율에 관련된 내용이었습니다.
이번에 다루어 볼 내용은 학습이 어려운 문제에 대하여 다루어 보려고 합니다.
학습이 어려운 이유는 크게 2가지 문제 입니다. 첫번째가 gradient vanishing 문제이고 두번째가 over fitting 문제이지요.
먼저 Inception에서 다룬 것은 깊은 layer까지 정보를 전달하기 위하여 auxiliary layer를 사용한 것입니다.
- 일반적인 네트워크에서는 마지막의 output에 해당하는 값과 label 값을 비교하여 오차를 구하고 그 오차를 통해 backpropagation 하는 방법을 이용하는데 inception에서는 layer가 깊어짐으로 인해 발생하는 gradient vanishing 문제를 해결하기 위해 중간 중간에도 오차를 계산하여 backpropagation을 전달하는 auxiliary layer를 추가적으로 두게 됩니다.
또한 overfitting이 덜 되는 general한 구조를 만들기 위해서는 sparse한 convolution을 도입하는 방법을 사용합니다.
- 마치 dropout을 적용하듯이 네트워크 자체를 sparse 하게 만드는 것이 개선점입니다.
- 앞에서 다룬 내용과 종합하면 matrix 자체는 dense하게 만들되 네트워크 자체는 sparse 하도록 만드는 것을 고민하였다고 할 수 있겠습니다.

Inception Module (v1)

앞에서 살펴본 motivation을 바탕으로 만들게 된 것이 Inception module 입니다.

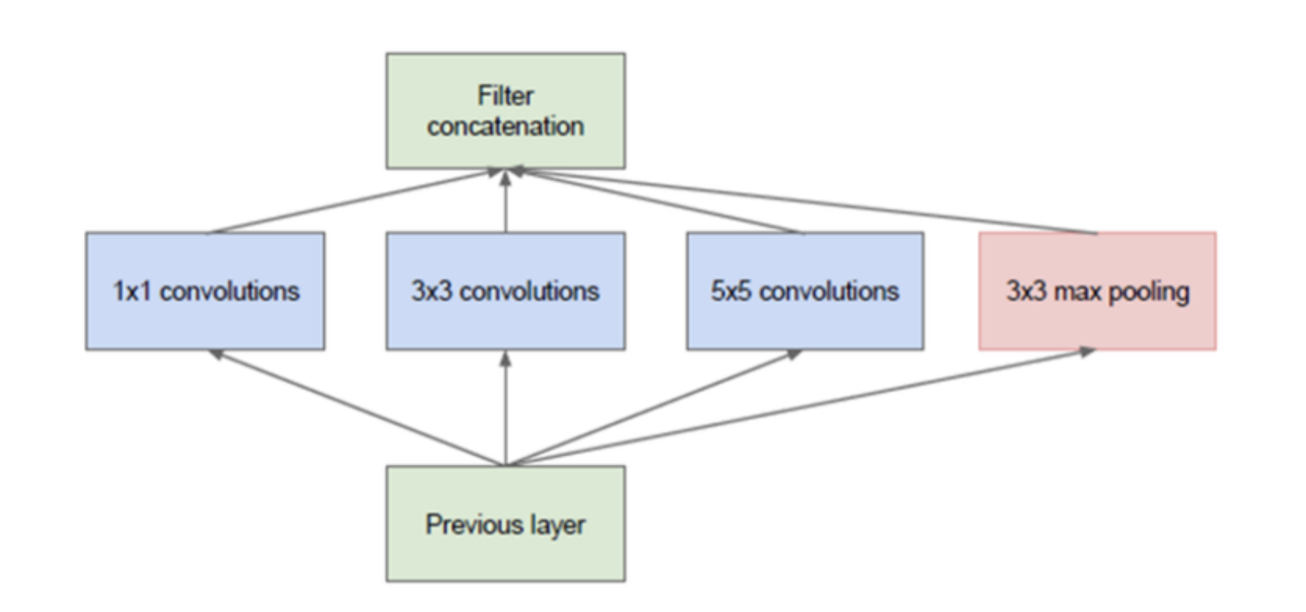
위 모듈을 보면 다양한 크기의 convolution filter가 있습니다.
이는 다양한 feature를 뽑기 위하여 여러 종류의 convolution filter를 병렬로 사용한 것인데
위 그림은 기본적인 Inception 모듈(naive version)에 해당합니다. 이전 레이어의 출력에 다양한 필터 크기로 합성곱 연산을 한 것을 확인 할 수 있습니다.
여기서 사용한 convolution 필터는 1x1, 3x3, 5x5 이고 추가적으로 3x3 맥스 풀링을 사용하였는데 이렇게 다양한 필터를 사용한 이유는 input feature에서 의미있는 feature를 뽑아내기 위해서는 다양한 representation을 받아들일 수 있는 필터들이 필요하기 때문입니다.
input feature의 어떤 특징이 있다고 할 때, 그 특징들과 필터 간의 correlation이 어떻게 분포되어 있는지 모르기 때문에 다양한 필터를 사용했다고 이해하시면 됩니다.
이런 이유로 Inception을 개발할 당시에는 다양한 필터를 병렬적으로 사용하는 것이 좋다고 판단하여 위 그림 처럼 사용하게 되었습니다.
다른 글에서 설명하였지만 convolution filter의 경우 이미지 내의 detail한 특성을 잡아낼 수 있고 MaxPooling 같은 경우 invariant한 특성을 잡아낼 수 있기 때문에, 이 두 종류를 같이 사용하였습니다.
논문에서 표현하기로는 다양한 feature를 뽑기 위해 여러 convolution filter를 병렬로 사용하는 것을 local sparse structure conv라고 설명하였고 이것이 네트워크 전체가 sparse 해지게 되어 앞에서 설명한 학습에 유리한 조건이 된다고 말합니다.
또한 convolution filter와 MaxPooling을 concatenation 연산으로 합칠 때, 이것을 dense matrix 연산으로 표현하였고 앞에서 설명한 효율적인 연산 방법에 해당한다고 설명하였습니다.

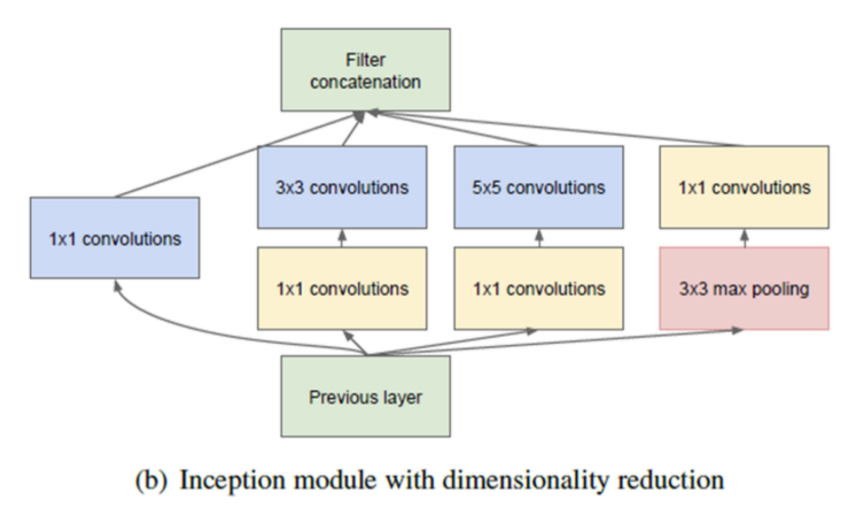
앞에서 살펴본 naive version의 Inception module에서 한발 더 나아가 1x1 convolution을 적용하여 채널 수를 줄여 파라미터의 수를 더 줄이는 방향으로 모듈을 설계하였습니다. (참고로 pooling에서는 width, height의 resolution은 감소하였지만 concat하기 위한 크기를 맞추기 위해 채널은 감소하지 않았습니다.)
또한 1x1 convolution을 이용하면 채널의 수를 마음대로 조절할 수 있기 때문에, concatenation 할 때 채널의 크기를 맞추는 데에도 용이합니다.

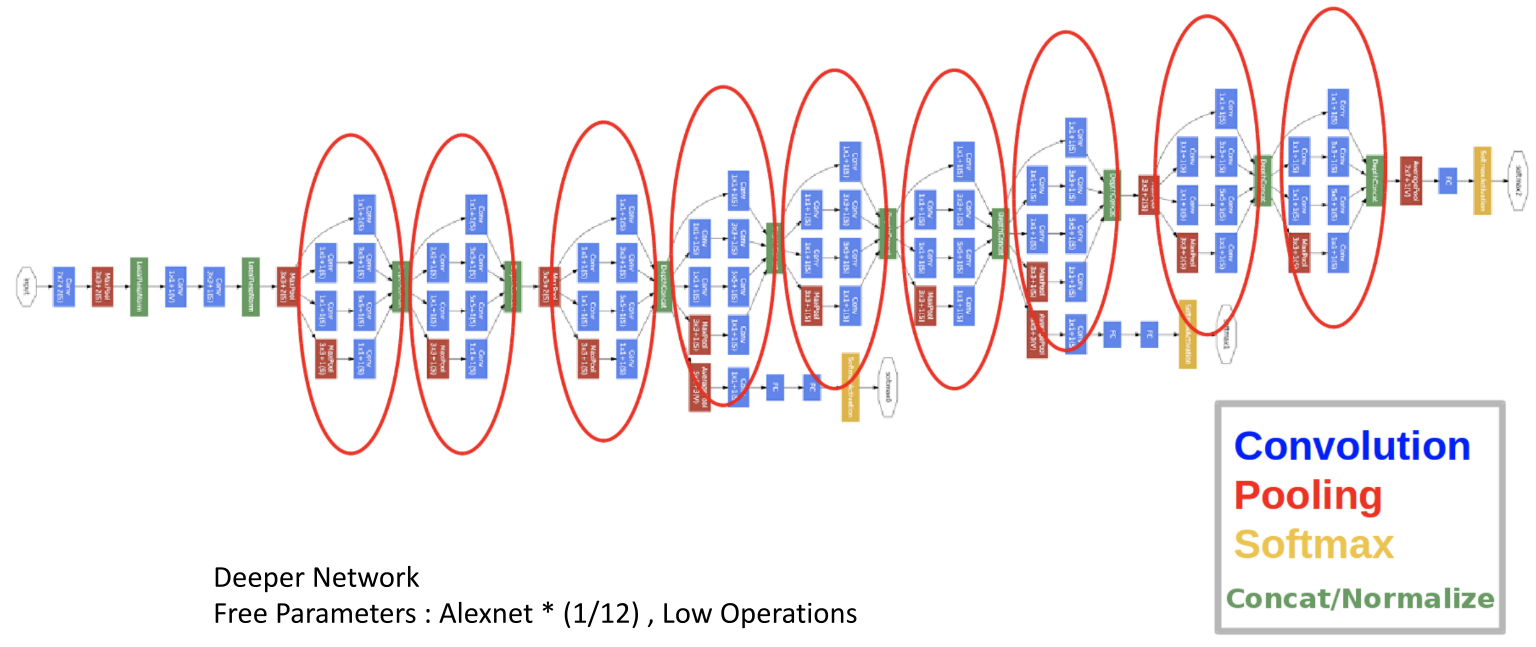
앞의 Inception module을 이용하여 위 아키텍쳐 처럼 네트워크를 완성 시킨것이 Inception v1 (GoogLeNet)이 되겠습니다.
결과적으로 성능도 올리면서 그 당시에 유명했던 AlexNet의 1/12배 파라미터를 사용한 것과 더 적은 연산을 사용한 것에 의의가 있었습니다.

Auxiliary Loss

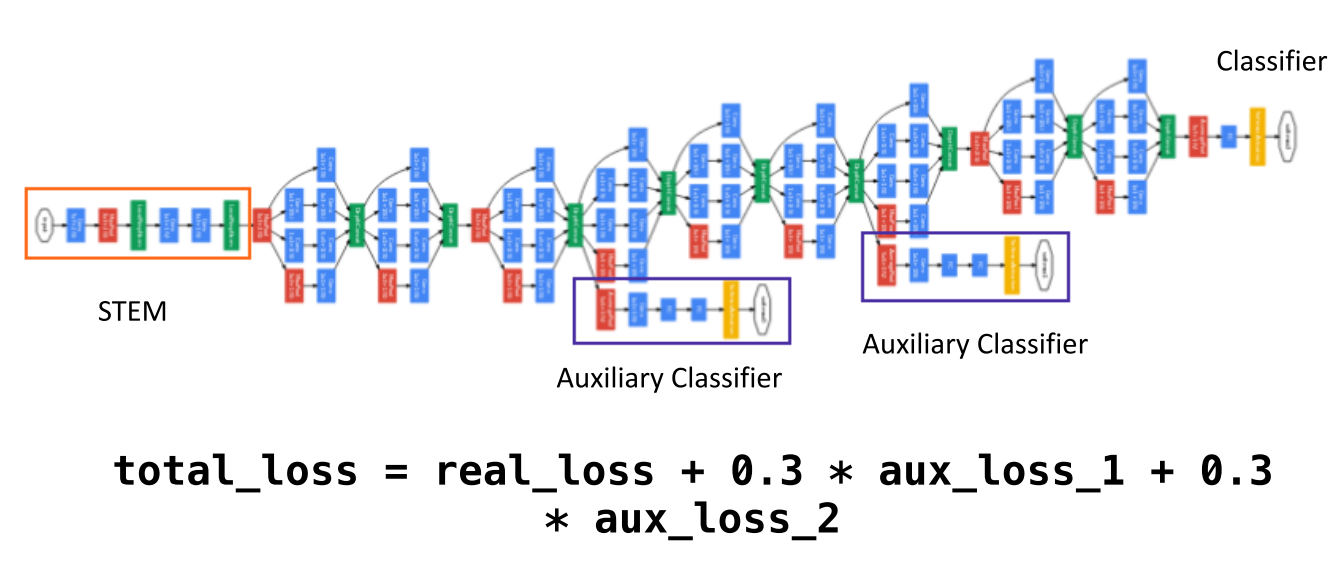
Auxiliary Loss 깊어진 layer에서 발생하는 vanishing gradient 문제를 개선하기 위하여 적용된 트릭입니다.
중간 중간에 Loss를 계산할 수 있는 layer를 추가적으로 만들어서 최종 loss에 반영하게 됩니다.
- 즉 label이 있으면 최종 output에서 loss를 계산할 때 사용하고 중간 중간에도 있는 Auxiliary loss에서도 값을 계산해서 반영합니다.
물론 최종 output에 의해 계산된 loss가 더 중요하므로 가중치를 더 줘야 하는 것이 합당합니다. 위 그림을 보면 Loss를 어떻게 주는 지 볼 수 있습니다.
실제 output에 의해 계산된 loss가 100%라면 auxiliary loss에는 30%의 가중치만 준 것을 알 수 있습니다.
여기서 사용된 auxiliary loss는 training 할 때에만 사용되고 inference할 때에는 사용되지 않습니다. 당연히 최종 출력은 하나만 나와야 하니 가장 중요한 최종 output을 사용하는 것이 합당합니다.

BN(Batch Normalization) Inception

그 다음으로 살펴 볼 것은 Inception에 Batch normalization을 적용한 것입니다. 요즘에는 BN의 개념이 일반화되고 그 효과도 입증되어 많은 딥러닝 네트워크에서 사용되고 있기에 관련 내용은 친숙하게 살펴보실 수 있을 것입니다.
만약 Batch normalization에 대한 내용을 참조하시려면 다음 링크를 확인해 보세요 : https://gaussian37.github.io/dl-concept-batchnorm/
그러면 BN Inception에 대하여 간단하게 살펴보겠습니다.

위 식과 같이 BN은 학습의 안정성을 위하여 각각의 학습 데이터 batch 마다 normalization을 해줍니다.
이 mini batch의 평균과 분산을 구하여 normalization을 하고 학습을 통하여 normalization 한 결과에 곱할 scale과 더할 shift 값을 구하게 됩니다.
따라서 최종적으로 normalization * scale + shift가 출력이 되고 이 값이 안정적인 학습에 도움이 되게 됩니다.
- scale과 shift는 batch가 학습이 잘되는 공간에 맵핑 하기 위한 변환 값이라고 보시면 되고 학습을 통해 최적의 값을 구하게 되니 어떤 값을 사용해야 할 지 정할 문제는 없습니다.

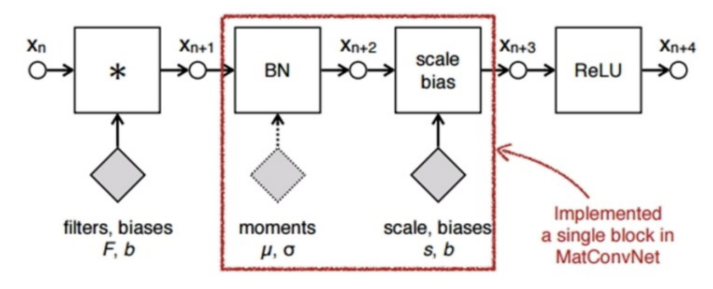
Batch Normalization은 위 그림과 같이 Convolution filter를 적용하고 Activation을 적용하기 이전 그 사이에 사용하고 있습니다. (Batch Normalization 논문 참조)
따라서 Inception module에서 Convolution - BN - ReLU 순서로 적용하면 됩니다.

Tensor Factorization

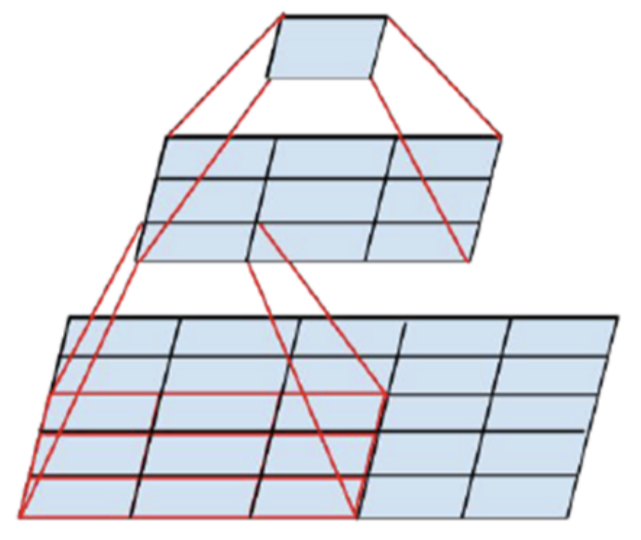
앞에서 간략하게 설명한 Tensor Factorization에 대하여 자세하게 알아보겠습니다.
위 그림의 가장 아래 필터를 보면 5x5 convolution 필터가 있는데 만약 5x5 convolution 필터를 한번 거친다면 그 영역에 해당하는 output은 크기가 1x1인 feature가 됩니다.
그런데 위 그림 처럼 5x5 영역에 3x3 convolution 필터를 stride = 1로 이동하면서 9군데 부분(width, height 방향으로 3칸씩 이동)에 convolution 연산을 하고 그 연산의 output인 3x3 영역의 feature를 다시 3x3 convolution 하게 되면 그 결과 또한 1x1 feature가 됩니다.
여기서 살펴볼 것은 5x5 convolution을 바로 적용하면 필터에 25개의 파라미터가 존재하게 되지만 3x3 convolution을 2번 사용하게 되면 18개의 파라미터만을 사용하게 됩니다. 물론 연산량은 더 증가하게 되지만 말이죠.
이런 트릭을 이용하면 같은 크기의 output feature를 만드는 데 파라미터의 숫자를 줄일 수 있습니다.

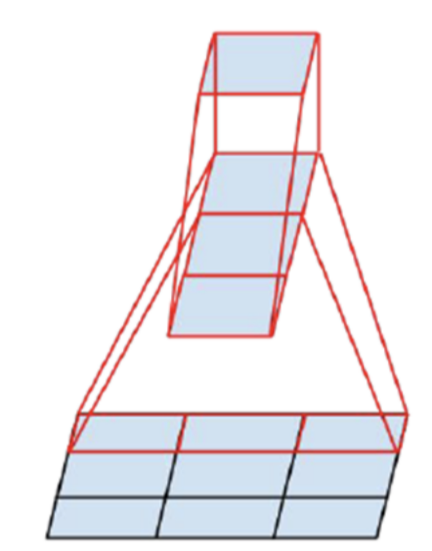
위 케이스도 동일하게 적용할 수 있습니다.
3x3 convolution 필터를 적용해서 1x1 output feature를 만드는 데에 9개의 파라미터를 사용할 수도 있지만 3x1 convolution 필터와 1x3 convolution 필터를 이용하면 6개의 파라미터를 사용하여 동일한 출력을 만들어 낼 수도 있습니다.

Inception v2, v3

처음에 살펴본 Inception module은 Inception v1(GoogLeNet)에 해당하는 딥러닝 네트워크이고 직전에 다른 Tensor Factorization등의 최적화 기법들을 적용한 것이 개선된 버전인 v2, v3 버전입니다.

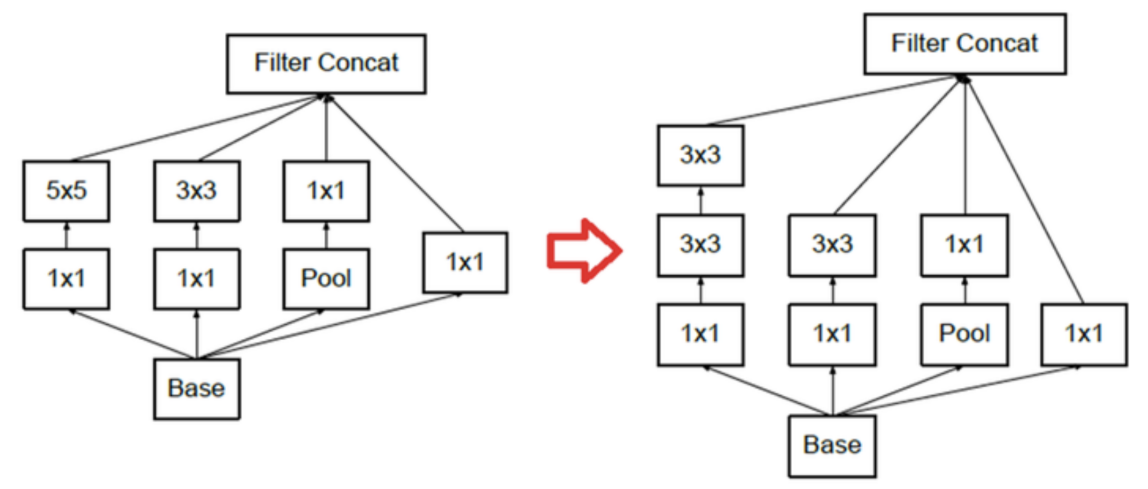
먼저 위 처럼 inception module을 개선한 것이 Inception Module A 라고 하고 inception v2에 사용됩니다.
물론 inception v3의 레이어에서도 사용이 됩니다.

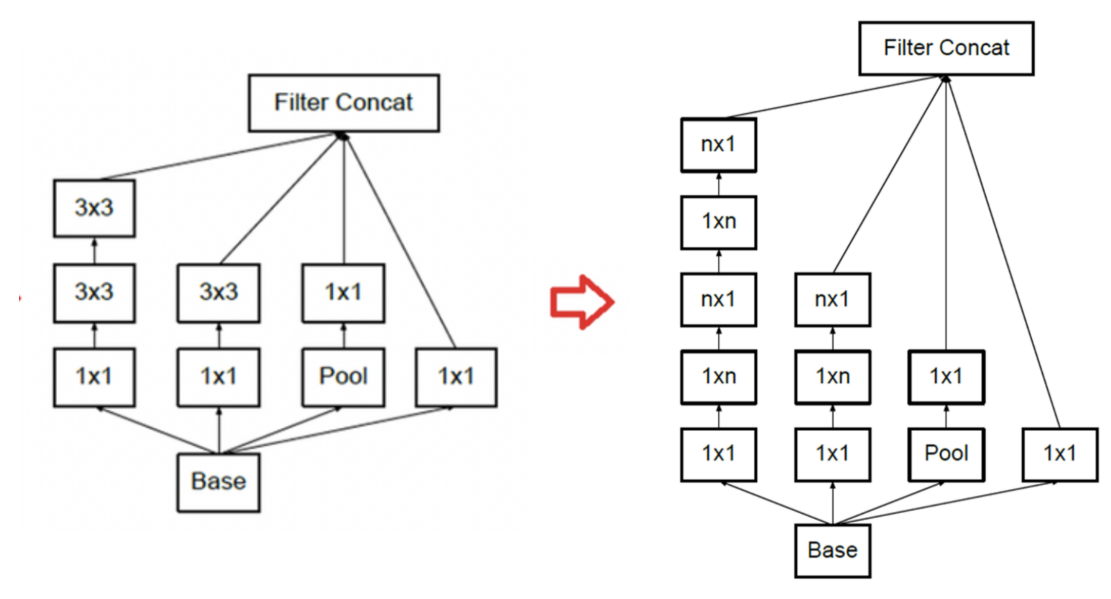
앞에서 설명한 것과 같이 1xn, nx1 convolution을 적용하여 최적화 한것을 Inception Module B 라고 합니다. 이 모듈에서는 모듈 A에 비해 연산량을 33% 절감하였다고 논문에서 설명합니다.
위에서 n에 3을 대입하면 개선 전/후가 대응이 됩니다.
위 방식은 Inception v3에서 부터 적용됩니다.

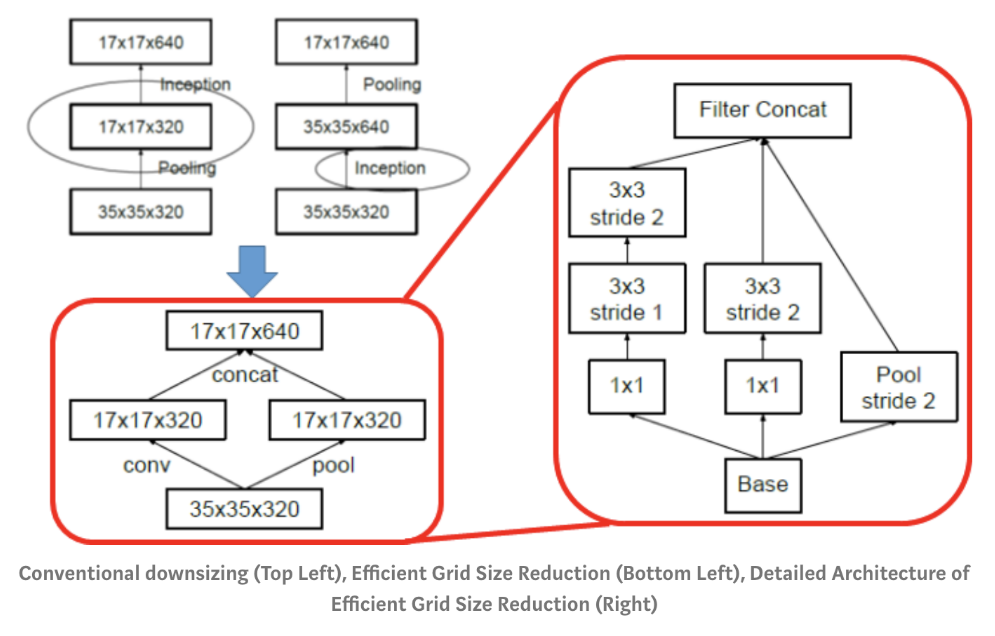
resolution을 줄이기 위한 방법으로는 크게 2가지가 있습니다. Convolution 연산 시 stride를 2 이상으로 가져가거나, Pooling을 하는 것입니다.
이 때, Convolution 연산의 stride를 적용하여 resolution을 줄이게 되면 연산량이 다소 많아지게 되고 반면 Pooling을 이용하여 resolution을 줄이면 Representational Bottleneck 이라는 문제가 발생하는 데 말 그대로 resolution이 갑자기 확 줄어들어서 정보를 잃게 되는 것을 말합니다.
그래서 Convolution 연산의 stride 적용과 MaxPooling을 병렬적으로 하는 방법을 적용하는 Grid Size Reduction 방법이 Inception Module v1부터 전체적으로 반영이 되어있습니다.

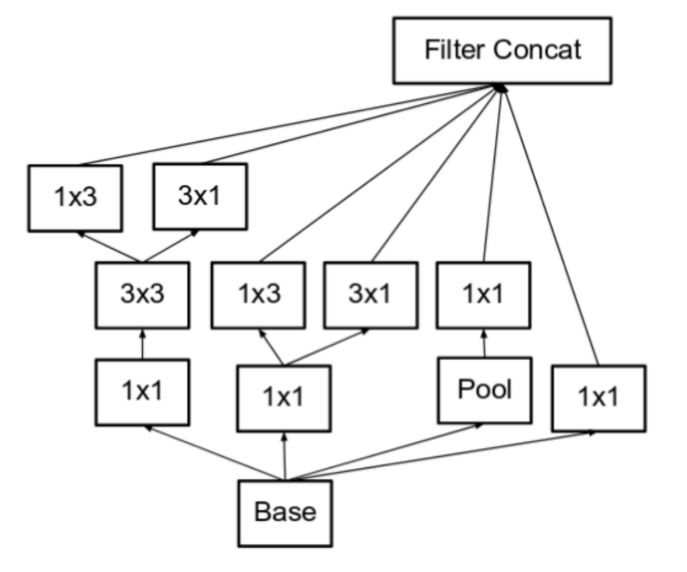
마지막으로 소개할 Inception Module C는 직전에 언급한 Representational Bottleneck 문제를 완화하기 위해서 좀 더 깊게가 아닌 좀더 넓게 concatenation 하는 방법으로 만들어본 모듈입니다.
모듈 내부에서 Convolution + stride나 Pooling이 깊게 적용되면 Representational Bottleneck문제가 더 악화되니 옆으로 쌓아보려는 시도라고 보시면 됩니다.
이 모듈은 Inception v3에서 output 단에 사용되었습니다.

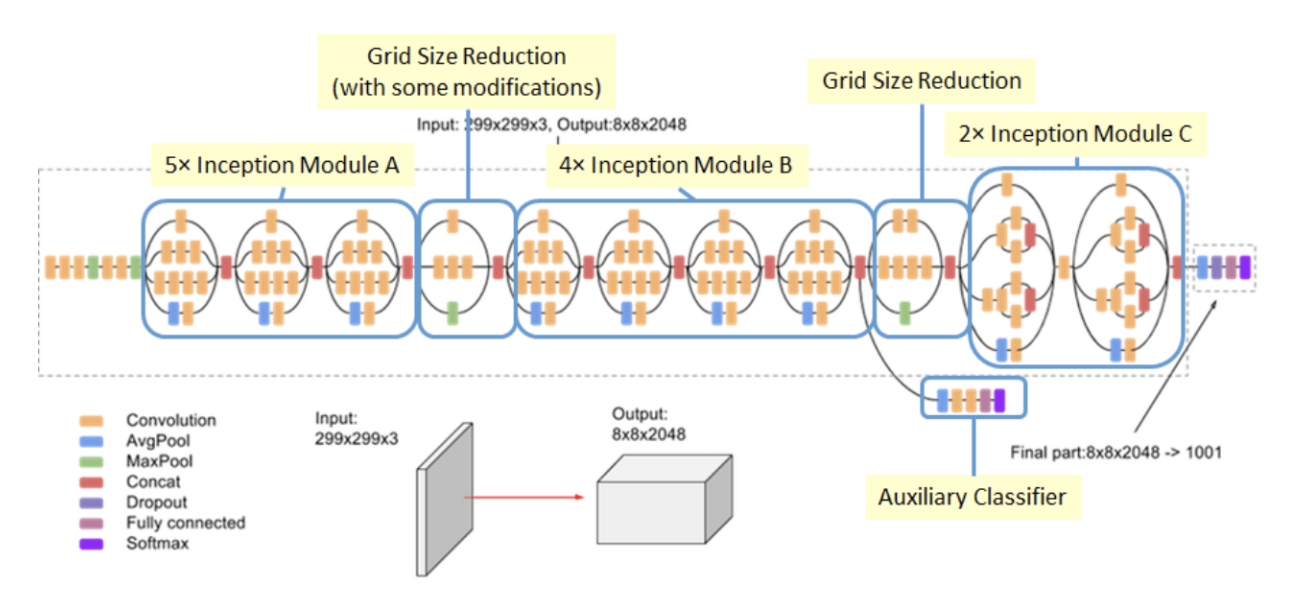
위 네트워크 아키텍쳐가 Inception v3가 되겠습니다.
앞에서 설명한 Inception Module A, B, C 그리고 Grid Size Reduction이 적용된 형태입니다.
처음에 살펴본 Inception v1 GoogLeNet에서 적용된 Auxiliary Loss는 2개였는데 1개로 축소되었는데 사실상 효과가 크게 좋지 않았기 때문이라고 유추할 수 있습니다. 현재 이런 Loss를 쓰는 네트워크는 거의 없으니 말이지요.

Pytorch 코드

이번 글에서 살펴 볼 Pytorch 코드는 Inception v1, GoogLeNet 입니다. 가장 기본이 되는 코드이니 이 코드를 이해하시면 다른 버전을 작성하는 데에도 큰 무리는 없을 것입니다.
앞에서 살펴본 Inception Module에 대한 내용을 다시 한번 정리하면서 Pytorch 코드에 대하여 살펴보도록 하겠습니다.
살펴본 것 처럼 네트워크 전체의 구조가 다소 복잡한 감이 있지만 자세히 살펴보면 반복적인 형태를 띄기 때문에 하나씩 모듈별로 하나씩 살펴보면 코드를 이해하힐 수 있을 것입니다.

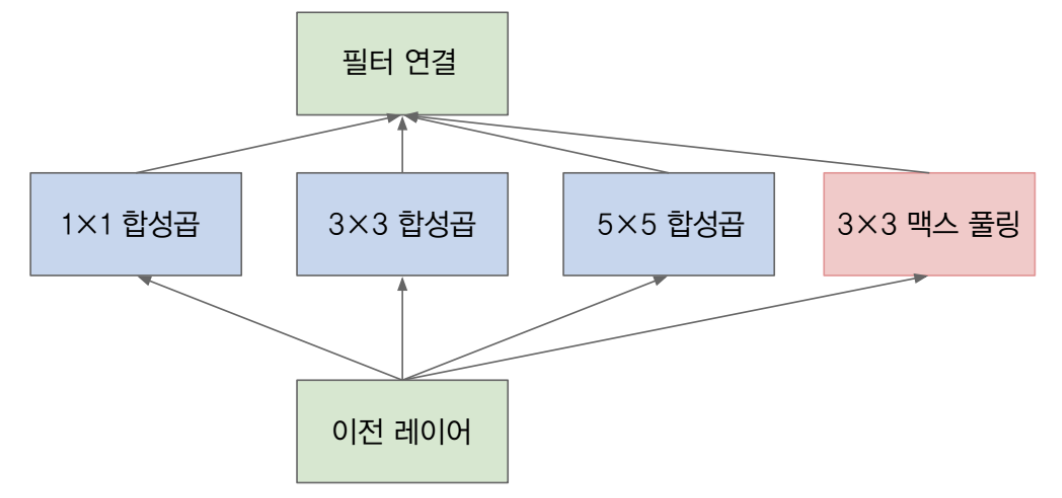
위 그림은 기본적인 Inception 모듈에 해당합니다. 이전 레이어의 출력에 다양한 필터 크기로 합성곱 연산을 한 것을 확인 할 수 있습니다.
여기서 사용한 convolution 필터는 1x1, 3x3, 5x5 이고 추가적으로 3x3 맥스 풀링을 사용하였습니다.

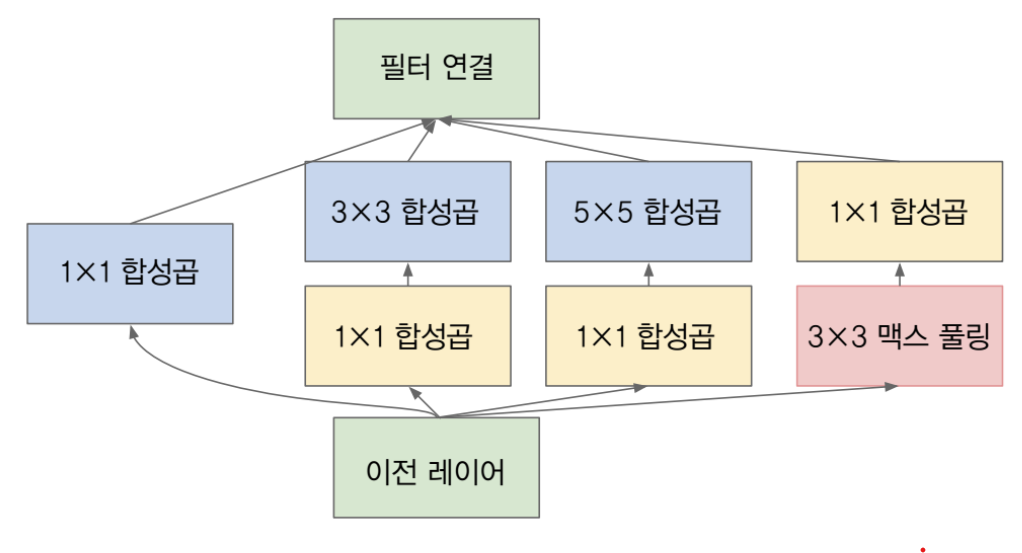
이번에 다루어 볼 코드는 기본적인 Inception 모듈에서 각각의 연산에 1x1 convolution이 추가된 형태를 알아보려고 합니다.
이 코드 형태를 이해하면 다른 버전의 Inception을 이해하는 것에도 어려움이 없을 것으로 판단됩니다.
먼저 1x1 convolution을 사용한 이유를 살펴보면 앞에서도 설명한 것과 같이 메모리 사용 절약의 측면이 큰 이유가 됩니다.

1x1 convolution 연산을 이용하면 위 그림과 같이 width와 height의 크기는 유지한 상태에서 channel의 크기만 변경 가능합니다.
channel의 크기를 줄이게 되면 메모리를 절약할 수 있습니다.
또한 위 그림을 기준으로 보면 1x1 convolution은 이미지의 width height 기준으로 하나의 픽셀만을 입력으로 받지만 채널 관점에서 봤을 때에는 채널의 갯수만큼의 입력을 받아서 하나의 결과를 생성하고 이를 목표 채널 수 만큼 반복합니다.
위 그림에서 왼쪽을 1 x 1 x 3 크기의 feature라고 하고 오른쪽을 1 x 1 x 5 크기의 feature라고 한다면 1 x 1 x 3 feature의 width와 height가 같은 위치의 (e.g. (1, 1)) feature들을 이용하여 같은 위치의 1 x 1 x 5 feature를 만들어 냅니다.
또한 각 width, height 위치의 채널들이 서로 대응되므로 Fully Connected Layer의 성격도 띄게 됩니다. 물론 FC layer처럼 filter의 위치 속성을 없애지 않고 계속 유지한다는 장점도 있습니다.
즉 정리하면, 1 x 1 convolution을 이용하여 메모리를 절약할 수도 있고 FC layer와 같이 filter 간의 연결도 하면서 feature에서의 공간을 무너뜨리지 않기에 성능 향상에 도움이 됩니다.

실제 Inception 모듈에 적용해 보면 기본적인 Inception 모듈에서는 128개 채널에서 256개 채널로 늘어나는 연산이었다면 1x1 convolution이 적용된 Inception 모듈에서는 1x1 convoltuion을 통해 채널의 수를 128개에서 32개로 줄인 다음에 다시 convolution 연산을 통하여 256개 채널로 늘립니다.
이렇게 적용하면 기존 연산보다 메모리 사용을 줄일 수 있습니다.

인셉션 모듈에는 1x1 연산, 1x1 연산 + 3x3 연산, 1x1 연산 + 5x5 연산, 3x3 맥스 풀링 + 1x1 연산 이렇게 4가지 연산이 있고 각각의 연산들을 채널 차원으로 붙여줍니다.
참고로 nn.Conv2d 함수의 파라미터는 각각 #input_channels, #output_channels, kernel_size, stride, padding, dilation, groups, bias, padding_mode 순서이고 아래 코드에서 사용하는 것은 #input_channels, #output_channels, kernel_size, stride, padding 까지 입니다.

def conv_1(in_dim, out_dim):
    # 1x1 연산
    model = nn.Sequential(
        nn.Conv2d(in_dim, out_dim, 1, 1)
        nn.ReLU(),
    )
    return model

def conv_1_3(in_dim, mid_dim, out_dim):
    # 1x1 연산 + 3x3 연산
    model = nn.Sequential(
        nn.Conv2d(in_dim, mid_dim, 1, 1),
        nn.ReLU()
        nn.Conv2d(mid_dim, out_dim, 3, 1, 1),
        nn.ReLU()
    )
    return model

def conv_1_5(in_dim, mid_dim, out_dim):
    # 1x1 연산 + 5x5 연산
    model = nn.Sequential(
        nn.Conv2d(in_dim, mid_dim, 1, 1),
        nn.ReLU(),
        nn.Conv2d(mid_dim, out_dim, 5, 1, 2),
        nn.ReLU(),
    )
    return model

def max_3_1(in_dim, out_dim):
    # 3x3 맥스 풀링 + 1x1 연산
    model = nn.Sequential(
        nn.MaxPool2d(3, 1, 1),
        nn.Conv2d(in_dim, out_dim, 1, 1),
        nn.ReLU(),
    )
    return model

위 코드들을 조합하면 인셉션 모듈을 만들 수 있습니다.
위 코드의 함수명을 잘 살펴보면 앞에서 언급한 인셉션 모듈의 4개 부분에 해당하는 것을 확인하실 수 있습니다.

위 코드를 이용하여 Inception module을 만들어 보도록 하겠습니다.
아래 코드는 입력이 들어오면 4가지 연산을 따로 진행하고 마지막에 채널 방향으로 이를 붙여주는 모듈입니다.

class inception_module(nn.Module):
    def __init__(self, in_dim, out_dim_1, mid_dim_3, out_dim_3, mid_dim_5, out_dim_5, pool):
        super(inception_module, self).__init__()

        self.conv_1 = conv_1(in_dim, out_dim_1)
        self.conv_1_3 = conv_1_3(in_dim, mid_dim_3, out_dim_3),
        self.conv_1_5 = conv_1_5(in_dim, mid_dim_5, out_dim_5),
        self.max_3_1 = max_3_1(in_dim, pool)

    def forward(self, x):
        out_1 = self.conv_1(x)
        out_2 = self.conv_1_3(x)
        out_3 = self.conv_1_5(x)
        out_4 = self.max_3_1(x)
        output = torch.cat([out_1, out_2, out_3, out_4], 1)
        return output

마지막으로 위 Inception 모듈을 이용하여 GoogLeNet을 작성하면 다음과 같습니다.
처음 입력은 컬러 이미지 라는 가정 하에 3채널을 입력받습니다.
각 inception module의 input의 크기는 이전 inception module의 out_dim_1 + out_dim_3 + out_dim_5 + pool과 같습니다.

class GoogLeNet(nn.Module):
    def __init__(self, base_dim, num_classes = 2):
        super(GoogLeNet, self).__init__()
        self.layer_1 = nn.Sequential(
            nn.Conv2d(3, base_dim, 7, 2, 3),
            nn.MaxPool2d(3, 2, 1),
            nn.Conv2d(base_dim, base_dim * 3, 3, 1, 1),
            nn.MaxPool2d(3, 2, 1),
        )

        self.layer_2 = nn.Sequential(
            # inception_module(in_dim, out_dim_1, mid_dim_3, out_dim_3, mid_dim_5, out_dim_5, pool)
            inception_module(base_dim * 3, 64, 96, 128, 16, 32, 32),
            inception_module(base_dim * 4, 128, 128, 192, 32, 96, 64),
            nn.MaxPool2d(3, 2, 1),
        )

        self.layer_3 = nn.Sequential(
            # inception_module(in_dim, out_dim_1, mid_dim_3, out_dim_3, mid_dim_5, out_dim_5, pool)
            inception_module(480, 192, 96, 208, 16, 48, 64),
            inception_module(512, 160, 112, 224, 24, 64, 64),
            inception_module(512, 128, 128, 256, 24, 64, 64),
            inception_module(512, 112, 144, 288, 32, 64, 64),
            inception_module(528, 256, 160, 320, 32, 128, 128),
            nn.MaxPool2d(3, 2, 1),
        )

        self.layer_4 = nn.Sequential(
            # inception_module(in_dim, out_dim_1, mid_dim_3, out_dim_3, mid_dim_5, out_dim_5, pool)
            inception_module(832, 256, 160, 320, 32, 128, 128),
            inception_module(832, 384, 192, 384, 48, 128, 128),
            nn.AvgPool2d(7, 1),
        )

        self.layer_5 = nn.Dropout2d(0.4)
        self.fc_layer = nn.Linear(1024, num_classes)

    def forward(self, x):
        out = self.layer_1(x)
        out = self.layer_2(out)
        out = self.layer_3(out)
        out = self.layer_4(out)
        out = self.layer_5(out)
        out = out.view(out.size(0), -1)
        out = self.fc_layer(out)

        return out

목차

Inception motivation

Inception Module (v1)

Auxiliary Loss

BN(Batch Normalization) Inception

Tensor Factorization

Inception v2, v3

Pytorch 코드

Inception motivation

Inception Module (v1)

Auxiliary Loss

BN(Batch Normalization) Inception

Tensor Factorization

Inception v2, v3

Pytorch 코드