Basic Probability and Information Theory

참고자료

https://ratsgo.github.io/convex%20optimization/2017/12/26/convexfunction/

이번 글에서는 GAN을 다루기 전에 필요한 기본적인 확률과 정보이론을 다루어 보려고 합니다.

1) Probability Model
2) Discriminative Model
3) Bayesian Theory
4) Basic Information Theory

4) Basic Information Theory

이번에 다루어 볼 주제는 Entropy, KL divergence, Mutual Information입니다.
먼저 정보이론을 확률이론 및 결정이론과 비교하여 간단하게 식으로 알아보겠습니다.
Probability Theory
- 불확실성(Event, 변수등)에 대한 일어날 가능성을 모델링 하는 것입니다.
- 　$P(Y \vert X) = \frac{ P(X \vert Y)P(Y) }{ P(X) }$
Decision Theory
- 불확실한 상황에서 추론에 근거해 결정을 내리는 것입니다.
- 　$Y = 1$, if $\frac{ P(x \vert y = 1)P(y=1) }{ P(x \vert y = 0)P(y=0) } > 1$
Information Theory
- 확률 분포 $P(x)$의 불확실성 정도를 평가하는 방법
- 　$H(X) = -\sum_{x}P(x)log_{2}P(x)$

그러면 먼저 간단하게 정보량(Information)이 무엇인지 알아보도록 하겠습니다.
예를 들어 1 ~ 16까지 16개 숫자 중에서 1개의 숫자를 하나 생각한 다음 다른 사람이 내가 생각한 숫자를 맞추도록 하려고 합니다. 이 때 최소 몇 번 물어야 할까요?
- 질문을 들으면 아시겠지만 이진 탐색으로 풀 수 있는 쉬운 문제입니다.
이 문제의 정답은 4번 입니다. 이진탐색으로 정답을 찾게 되면 $n = log_{2}16 = 4$(단위: bit)가 됩니다.
여기서 정보량을 정의할 수 있는데, 불확실함을 해소하기 위해 필요한 질문(정보)의 수(불확실한 정도)라고 할 수 있습니다.
특히, 정보량의 단위는 bit로 표현하게 됩니다. (Yes / No 대답에 해당합니다.)

여기서 정보량과 확률의 관계를 살펴보겠습니다.
카드 한장을 선택할 확률 $p = 1/16$으로 모두 동일합니다.
선택한 카드를 맞추기 위한 정보량을 확률 $p$를 이용해 표현해 보면
- 　$n = -log_{2}(p) = log_{2}(1/p) = log_{2}(16) = 4$ 가 됩니다.
일반적으로 어떤 사상의 확률이 $p$라고 하였을 때, 그 사상에 대한 정보량 $I$는 다음과 같습니다.
- 　$I = log_{2}(\frac{1}{p}) = -log_{2}(p)$
정보량을 계산하는 방법을 다음 예로 살펴보겠습니다.
- 주사위를 던져서 짝수의 눈이 나타날 사상 $E_{1}$의 정보량
  - 　$P(E_{1}) = \frac{1}{2} \to I = -log_{2}\frac{1}{2} = 1 (bit)$
- 주사위를 던져서 2의 눈이 나타날 사상 $E_{2}$의 정보량
  - 　$P(E_{2}) = \frac{1}{6} \to I = -log_{2}\frac{1}{6} = 2.584962...(bit)$
- 주사위를 던져서 1 ~ 6이 나타날 사상 $E_{3}$의 정보량
  - 　$P(E_{3}) = \frac{6}{6} = 1 \to I = -log_{2}1 = 0 (bit)$

이번에는 정보이론에서 중요한 개념인 Entropy에 대하여 알아보도록 하겠습니다.
카드 16장 중 임의의 카드 선택에 대한 평균적 정보량은 다음과 같이 계산할 수 있습니다.
　$H(X) = -\sum_{i=1}^{16} P(X=i)log_{2}P(X=i) \to \sum_{i=1}^{16}\frac{1}{16} * log_{2}(\frac{1}{16}) = 4(bit)$
이는 불확실성을 해소하기 위해서 평균적으로 4번의 질문이 필요하다는 의미입니다.
Entropy란 확률분포 $P(X)$에 대한 정보량의 기댓값입니다.
예를 들어 동전던지기를 하여 앞면, 뒷면의 발생 확률이 각각 1/2 일 때, 앞몇 뒷면을 맞추기 위해 필요한 평균적 정보량은 얼마일까요?
- 　$H(X) = -\sum_{X}P(X)log_{2}P(X) = H(P) = ( P(X=H) * (-logP(X=H)) ) \ + \ ( P(X=T) * (-logP(X=T)))$
- 　$= \frac{1}{2} * ( -log_{2}(\frac{1}{2})) + \frac{1}{2} * (-log_{2}(\frac{1}{2})) = 1(bit)$
- 따라서 동전을 던졌을 때, 앞면 또는 뒷면을 맞추기 위해 필요한 질문의 횟수(정보량)은 1번입니다.
또다른 예로 초록공과 붉은공을 선택할 확률이 각각 2/8, 6/8이라고 할 때, 초록공과 붉은공을 맞추기 위한 평균적 정보량은 얼마일까요?
- 　$H(X) = -\sum_{X}P(X)log_{2}P(X) = \frac{2}{8} * (-log_{2}(\frac{2}{8})) + \frac{6}{8} * (-log_{2}(\frac{6}{8})) = 0.812277...(bit)$

위에서 다룬 동전 던지기의 예를 통해 엔트로피의 크기 변화에 대하여 알아보도록 하겠습니다.
동전의 앞면이 나올 확률 $P(X=Head) = p$라고 하고 뒷면이 나올 확률은 $P(X=Tail) = 1-p$라고 하겠습니다.
그러면 동전 던지기의 Entropy는 $H_{P} = -plog_{2}p - (1-p)log_{2}(1-p)$가 됩니다.
- 여기서 P는 동전의 앞면이 나올 확률이라고 가정하겠습니다.
가로축을 $P$, 세로축을 $H(P)$ 라고 하면 다음과 같은 Entropy 크기 변화 분포를 가지게 됩니다.

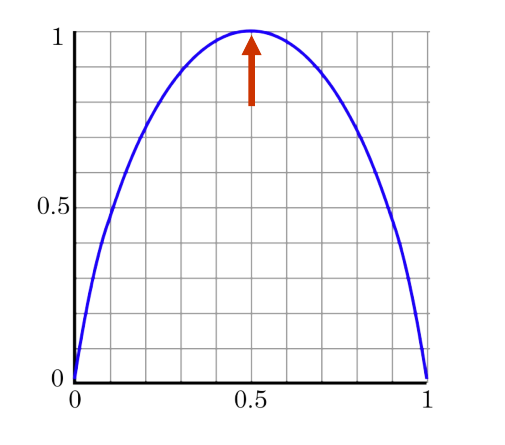
만약 동전의 앞면이 나올 확률이 0.5라면 $$ H(x) = -\sum_{x}P(x)logP(x) = -(0.5 * log_{2}0.5 + 0.5*log_{2}0.5) = 1
확률분포 $p(x)$에 따른 Entropy H(x)에 대한 성질을 보면 다음과 같습니다.

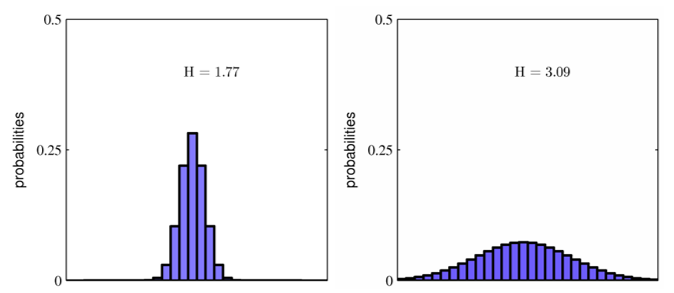
왼쪽 그림과 같이 불균형한 분포에서는 불확실성이 낮습니다. 특정 사건이 발생할 확률이 높기 때문에 예측이 가능하지요.
- 이런 경우 불확실성이 적으므로 Entropy 가 낮습니다.
오른쪽 그림과 같이 균등한 분포에서는 불확실성이 높습니다. 마치 주사위를 던졌을 때, 어느 눈이 나오기 예측하기 어려운것 처럼 예측하기가 어렵습니다.
- 이런 경우 불확실성이 크므로 Entropy가 높습니다.

Entropy에 관한 내용을 예시를 통하여 알아보았습니다. 그러면 Entropy 개념을 정확하게 한번 확인해보겠습니다.
Entropy는 확률 분포 $P(X)$에서 일어날 수 있는 모든 사건들의 정보량의 기댓값으로 $P(X)$의 불확실 정도를 평가합니다.
즉, $H_{P} = E_{X}[-log_{2}P(X)]$가 됩니다. 이 때, 상세 식은 이산형 변수와 연속형 변수에 따라서 나눌 수 있습니다.
- 이산형 확률 변수 : $H_{P} = -\sum_{X}P(X)log_{2}P(X)$
- 연속형 확률 변수 : $H_{P} = \int P(X)log_{2}P(X) dX$
Entropy의 성질에 대하여 정리해 보겠습니다.
- Entropy에서 정보량을 나타내는 $log_{2}$는 $ln$으로 바꿔서 사용할 수 있습니다.
- Entropy $H(X)$는 확률 분포 $P(X)$의 불확실 정도를 측정합니다.
- Entropy는 확률 분포 $P(X)$가 constant(혹은 uniform)할 때 최대화 된다.
- Entropy는 확률 분포 $P(X)$가 delta function일 때 최소화가 됩니다.
- Entropy는 항상 양수입니다.

Entropy는 Entropy encoding이란 내용과 연관이 있습니다. 엔트로피 인코딩은 심볼이 나올 확률에 따라 심볼을 나타내는 코드의 길이를 달리하는 부호화 방법입니다.
좋은 인코딩 방식은 실제 데이터 분포 $P(X)$를 알고 있을 때, 이에 반비례하게 코딩의 길이를 정하는 것입니다.
- Shannon’s source coding theorem에 따르면 최적의 코딩 길이는 $log\frac{1}{P(X)}$ 입니다.

이번에는 Entropy에 반대되는 개념인 Cross Entropy에 대하여 알아보도록 하겠습니다.
만약 실제 데이터 분포는 $P(X)$이지만, 우리가 실제 분포에 대해서 몰라서 분포 $Q(X)$를 대신 활용하면 어떨까요?
그러면 이 때의 정보량은 $$ H(P, Q) = \sum_{x}P(x)log\frac{1}{Q(x)}
Cross Entropy란 실제 데이터 $P$의 분포로부터 생성되지만, 분포 $Q$를 사용하여 정보량을 측정해서 계산한 평균적 정보량을 의미합니다.
- 여기서 $P$의 분포를 정확하게 모르기 때문에 $Q$의 분포를 사용한 것입니다.
일반적으로 $H(P, Q) \ge H(P)$와 같습니다. 즉, 데이터의 분포를 $Q$로 가정하고 심볼을 코딩하면, 실제의 분포 $P$를 가정한 최적의 코딩방식보다 평균적인 정보량이 커지게 됩니다.

앞에서 배운 Entropy와 Cross Entropy를 이용하여 유명한 개념 중 하나인 KL divergence를 이해할 수 있습니다.
Cross Entropy $H(P, Q)$는 Entropy $H(P)$보다 항상 크고 $P = Q$일 때에만 같기 때문에, 두 항의 차이를 분포 사이의 거리처럼 사용할 수 있습니다.
　$D_{KL}(P \Vert Q) = H(P, Q) - H(P)$
　$= \sum_{x} P(x)log\frac{1}{Q(x)} - P(x)log\frac{1}{P(x)} = \sum_{x}P(x)log\frac{P(x)}{Q(x)}$
데이터 인코딩 관점에서 보면 KL divergence는 데이터 소스의 분포인 $P$대신 다른 분포 $Q$를 사용해서 심볼을 인코딩하면 추가로 몇 bit가 낭비가 생기는 지 나타낸다고 해석 할 수 있습니다.
다시 말하면 KL divergence는 두 확률 분포 $P$와 $Q$의 차이를 측정합니다.

그러면 KL divergence의 성질에 대해서 알아보려고 합니다.
위에서 설명한 바와 같이 KL divergence는 데이터 소스의 분포인 $P$ 대신 다른 분포 $Q$를 사용해서 인코딩하면 추가로 몇 bit의 낭비가 생기는지 나타냅니다.
- 이 말은 즉, 확률 분포 P와 Q 사이의 차이와 같습니다.
따라서  D_{KL}(P \Vert Q) = H(P, Q) - H(P) = \sum_{x} P(x)log\frac{P(x)}{Q(x)} $$ 가 되고
이 식은 다음과 같은 성질을 가집니다.
- 1) $D_{KL}(P \Vert Q) \gt 0$
- 2) $D_{KL}(P \Vert Q) = 0 \ iff \ P = Q$
- 3) $D_{KL}(P \Vert Q) \ne D_{KL}(Q \Vert P)$ (Reverse KL)
- 4) $P$를 고정하고 $Q_{\theta}$를 움직일 때, $D_{KL}(P \Vert Q_{\theta})$ 변화는 $H(P, Q_{\theta})$의 변화와 같습니다.

KL divergence의 성질을 알아보기 위하여 Jensen's inequality에 대하여 알아보겠습니다.
Jensen's inequality는 아래로 볼록한 함수 $f$와 그 때의 정의역 $x$에서 정의됩니다.

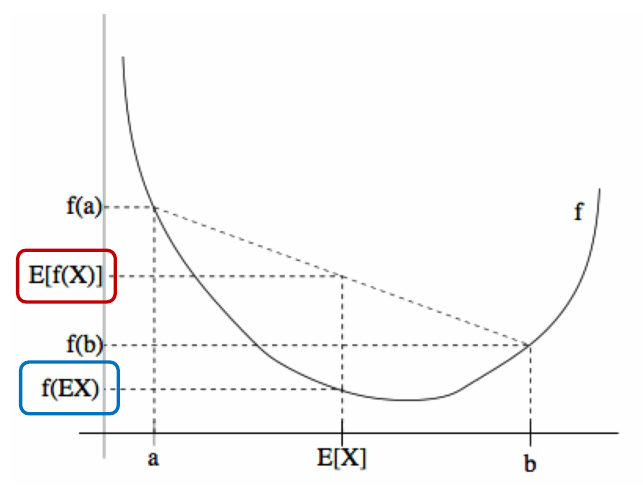
위 그래프와 같이 $f$함수가 convex형태(아래로 볼록)를 가질 때, $E[f(x)] \gt f(E[x])$가 됩니다.
이것을 기댓값 $E(X) = \sum_{i=1}^{N}x_{k}Pr(x=x_{k})$ 관점에서 아래로 볼록함수에 적용시켜 보도록 하겠습니다.
대표적인 아래로 볼록 함수 중에 $-log(x)$ 가 있습니다. 이 함수에 Jensen's inequality를 적용하면 다음과 같습니다.
- 　$E[-log(x)] \gt -log(E(x))$가 됩니다.
이것을 기댓값 관점에 적용시키면 $-\sum_{x} P(x)log(x) \gt -log(\sum_{x}P(x)*x)$ 가 됩니다.
이 식이 뜻하는 바는 …

그 다음은 위에서 설명한 성질 중 하나인 KL divergence는 양수이다 라는 명제를 증명해 보겠습니다. 이 때, Jensen's inequality를 사용하겠습니다.
　$D_{KL}(P \Vert Q) = H(P, Q) - H(P) = \sum P(X)log\frac{P(X)}{Q(X)} = -\sum P(X)log\frac{Q(X)}{P(X)} \gt -log(\sum P(X)\frac{Q(X)}{P(X)})$ (… Jensen's inequality)
　$= -log(\sum Q(X)) = -log(1) = 0$이 됩니다. 따라서 $H(P, Q) \gt H(P)$ 가 됩니다. (이를 Gibbs inequality)라고 합니다.

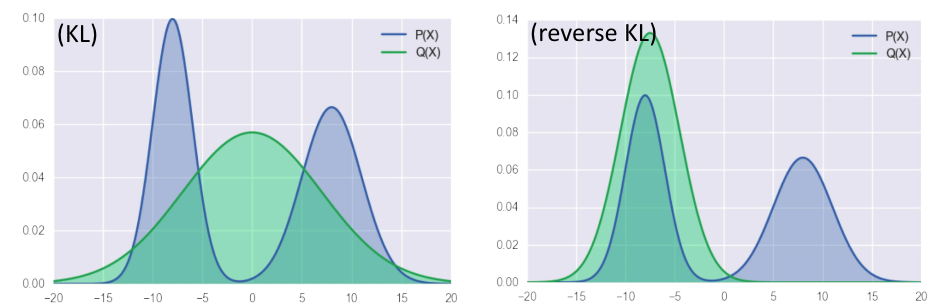
그 다음으로 KL divergence와 Reverse KL divergence에 대하여 알아보겠습니다.
유명한 성질 중 하나인 KL divergence는 거리함수가 아니다라는 명제입니다. 왜냐하면 교환법칙이 성립하지 않기 때문입니다.
여기서 KL divergence와 Reverse KL divergence는 다음과 같습니다.
- KL divergence : $D_{KL}(P \Vert Q_{\theta})$
- Reverse KL divergence : $D_{KL}(Q_{\theta} \Vert P)$
결과적으로 값을 계산해보면 두 분포의 값은 서로 다르므로 $P$와 $Q$의 교환법칙이 성립하지 않으므로 거리함수라고 정의할 수는 없습니다.
하지만, 두 분포가 다를수록 큰 값을 가지며 둘이 일치할 때에만 0이 되기 때문에 거리와 비슷한 용도로 사용할 수 있습니다.

다음으로 KL divergence와 log-likelihood의 관계에 대하여 알아보겠습니다.
만약 $P$가 실제 데이터 분포(empirical distribution)이고 $Q_{\theta}$가 우리가 설계하는 확률 모델이라면 $D_{KL}(P \Vert Q_{\theta})$를 최소화 하는 것은, 우리 모형의 log-likelihood를 최대화 하는 것과 같습니다.
　$D_{KL}[P(x \vert \theta^{*})]$ : Data distribution with true parameter $\theta^{*}$
　$D_{KL}[P(x \vert \theta)]$ : Our model with tunable parameter $\theta$
위 두가지 정의를 이용하여 KL divergence를 구해보면 다음과 같습니다.
- 　$D_{KL}[P(x \vert \theta^{*}) \Vert P(x \vert \theta)]$
- 　$= \mathbb E_{x ~ P(x \vert \theta^(*))}[log\frac{ P(x \vert \theta^{*}) }{ P(x \vert \theta) }]$
- 　$= \mathbb E_{x ~ P(x \vert \theta^(*))}[logP(x \vert \theta^{*}) - logP(x \vert \theta)]$
- 　$= \mathbb E_{x ~ P(x \vert \theta^(*))}[logP(x \vert \theta^{*})] - \mathbb E_{x ~ P(x \vert \theta^(*))}[logP(x \vert \theta)$
이 식은 KL divergence이므로 항상 0보다 크거나 같습니다. 이 식이 최소가 되기 위해서는 따라서 2번째 항인 $\mathbb E_{x ~ P(x \vert \theta^(*))}[logP(x \vert \theta)$이 최대가 되어야 합니다.
- 이 식이 최소화 된다는 것은 확률 모델 $P$와 $Q_{\theta}$ 가 같다는 뜻입니다.
식 $-\mathbb E_{x ~ P(x \vert \theta^(*))}[logP(x \vert \theta) = -\frac{1}{N} \sum_{i}^{N}logP(x_{i} \vert \theta)$ 가 됩니다.
- 이 값은 NLL(Negative Log Likelihood)로 이 값을 최소화 하는 것과 Log Likelihood를 최대화 하는 것은 같은 의미를 가집니다.(부호 차이)
- 즉, $D_{KL}(P \Vert Q_{\theta})$ 를 최소화하는 Maximum Likelihood를 찾아야합니다.

마지막으로 정보 이론에 대하여 정리해 보도록 하겠습니다.
Entropy는 확률 분포 $p(x)$에서 일어날 수 있는 모든 사건들의 정보량의 기댓값으로 $p(x)$의 불확실성 정도를 나타냅니다.
Cross Entropy는 실제 데이터 $P$의 분포로부터 생성되지만, 분포 Q를 사용하여 정보량을 측정해서 나타낸 평균적 bit수를 의미합니다.
KL divergence는 두 확률 분포 $P$와 $Q$의 차이를 측정합니다.
Mutual Information은 두 확률 변수들이 얼마나 서로 dependent한 지 측정합니다.