MobileNets - Efficient Convolutional Neural Networks for Mobile Vision Applications
2017, Apr 17
- 이번 글에서는 경량화 네트워크로 유명한
MobileNet에 대하여 알아보도록 하겠습니다.- 이번글은
MobileNet초기 버전(v1) 입니다.
- 이번글은
- MobileNet의 핵심 내용인
Depthwise Separable Convolution의 내용을 퀵 하게 알고 싶으면 저의 다른 글도 추천 드립니다. - 아래 글의 내용은 PR12 모바일넷 설명 내용을 글로 읽을 수 있게 옮겼습니다.
목차
-
1. 논문 리뷰 (PR12 영상으로 대체)
-
1.1. 경량화 네트워크의 필요성
-
1.2. Small Deep Neural Network 기법
-
-
2. Pytorch 코드 리뷰
1. 논문 리뷰 (PR12 영상으로 대체)
1.1. 경량화 네트워크의 필요성
- 먼저 딥러닝의 상용화를 위하여 필요한 여러가지 제약 사항을 개선시키기 위하여 경량화 네트워크에 대한 연구가 시작되었습니다.
- 딥러닝을 이용한 상품들이 다양한 환경에서 사용되는데 특히, 고성능 컴퓨터가 아닌 상황에서 가벼운 네트워크가 필요하게 됩니다.
- 예를 들어 데이터 센터의 서버나 스마트폰, 자율주행자동차 또는 드론과 같이 가격을 무작정 높일 수 없어서 제한된 하드웨어에 딥러닝 어플리케이션이 들어가는 경우입니다.
- 이러한 경우에 실시간 처리가 될 정도 성능의 뉴럴넷이 필요하고 또한 얼마나 전력을 사용할 지도 고려를 해야합니다.
- 이러한 제약 사항을 충분히 만족하면서 또한 아래와 같은 성능이 꽤 괜찮아야 어플리케이션에 적용을 할 수 있습니다.
- 충분히 납득할만한 정확도
- 낮은 계산 복잡도
- 저전력 사용
- 작은 모델 크기
- 그러면 왜
Small Deep Neural Network가 중요하게 되었을까요?- 네트워크를 작게 만들면 학습이 빠르게 될것이고 임베디드 환경에서 딥러닝을 구성하기에 더 적합해집니다.
- 그리고 무선 업데이트로 딥 뉴럴 네트워크를 업데이트 해야한다면 적은 용량으로 빠르게 업데이트 해주어야 업데이트의 신뢰도와 통신 비용등에 도움이 됩니다.
1.2. Small Deep Neural Network 기법
Channel Reduction: MobileNet 적용- Channel 숫자룰 줄여서 경량화
Depthwise Seperable Convolution: MobileNet 적용- 이 컨셉은
Xception에서 가져온 컨셉이고 이 방법으로 경량화를 할 수 있습니다.
- 이 컨셉은
Distillation & Compression: MobileNet 적용- Remove Fully-Connected Layers
- 파라미터의 90% 정도가 FC layer에 분포되어 있는 만큼 FC layer를 제거하면 경량화가 됩니다.
- CNN기준으로 필터(커널)들은 파라미터 쉐어링을 해서 다소 파라미터의 갯수가 작지만 FC layer에서는 파라미터 쉐어링을 하지 않기 때문에 엄청나게 많은 수의 파라미터가 존재하게 됩니다.
- Kernel Reduction (3 x 3 → 1 x 1)
- (3 x 3) 필터를 (1 x 1) 필터로 줄여서 연산량 또는 파라미터 수를 줄여보는 테크닉 입니다.
- 이 기법은 대표적으로
SqueezeNet에서 사용되었습니다.
- Evenly Spaced Downsampling
- Downsampling 하는 시점과 관련되어 있는 기법입니다.
- Downsampling을 초반에 많이 할 것인지 아니면 후반에 많이할 것인지 선택하게 되는데 그것을 극단적으로 하지 않고 균등하게 하자는 컨셉입니다.
- 왜냐하면 초반에 Downsampling을 많이하게 되면 네트워크 크기는 줄게 되지만 feature를 많이 잃게 되어 accuracy가 줄어들게 되고
- 후반에 Downsampling을 많이하게 되면 accuracy 면에서는 전자에 비하여 낫지만 네트워크의 크기가 많이 줄지는 않게 됩니다.
- 따라서 이것의 절충안으로 적절히 튜닝하면서 Downsampling을 하여 Accuracy와 경량화 두 가지를 모두 획득하자는 것입니다.
- Shuffle Operation
- 특히
MobileNet에서 사용하는 핵심 아이디어는Depthwise Seperable Convolution입니다.
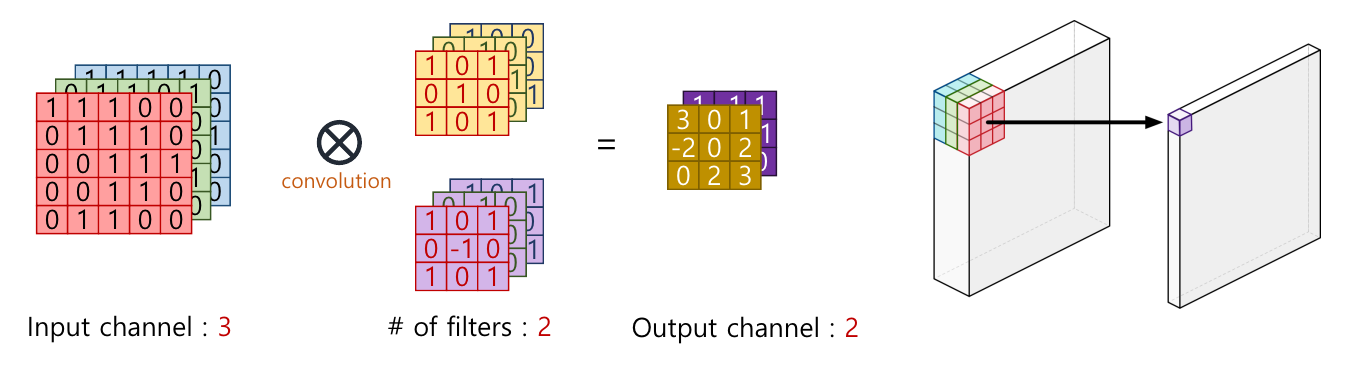
- 먼저
MobilNet을 다루기 전에 간단하게 Convolution Operation에 대하여 다루어 보겠습니다. - 위와 같이 인풋의 채널이 3개이면 convolution 연산을 하는 필터의 채널 또한 3개이어야 합니다.
- 이 때 필터의 갯수가 몇 개 인지에 따라서 아웃풋의 채널의 숫자가 결정되게 됩니다.
- 정리하면
인풋의 채널 수 = 필터의 채널 수이고필터의 갯수 = 아웃풀의 채널 수가 됩니다. - 이 때, 인풋 채널과 필터의 연산 과정은 위의 오른쪽 그림과 같이 입력 채널에서는 필터의 크기 만큼 모든 채널의 값들이 element-wise 곱으로 연산하여 최종적으로 한 개의 값으로 모두 더해지게 됩니다.
- 먼저 모바일넷 이전의 네트워크인
VGG의 네트워크 구조를 살펴보면 어떤 크기의 필터를 사용하는 것이 좋은가에 대한 솔루션을 제공하였습니다. - 3 x 3 크기의 필터를 여러번 사용하면 5 x 5 나 7 x 7 크기의 필터와 같은
receptive field를 가지기 때문에 3 x 3 필터만 쓰면 된다는 것을 제시하였습니다. - 그리고 3 x 3 필터를 여러번 사용하는 것이 더 큰 필터를 조금 사용하는 것 보다 더 non-linearity가 많아지게 되는 장점이 있고 파라미터 수는 오히려 더 작아지게 되므로(ex. 2 x (3 x 3 x C) Vs. (5 x 5 x C)) regularization에서도 우수한 성능이 보입니다.
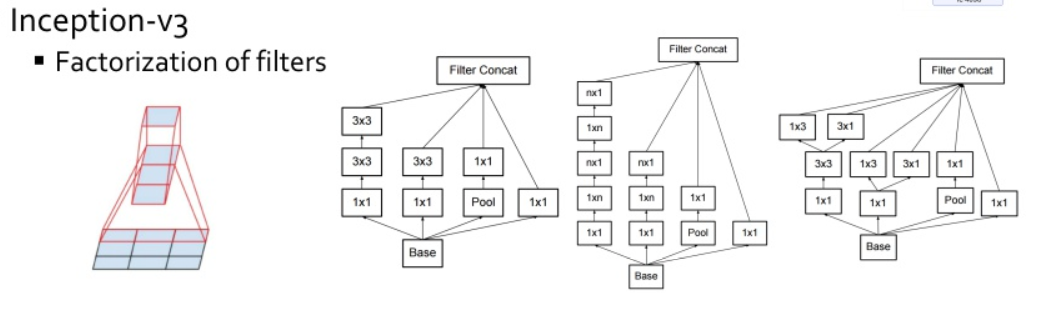
VGG의3 x 3 필터컨셉을 이용하여Inception v2, v3에서는 5 x 5나 7 x 7 필터를 지우고 3 x 3 필터만 사용하게 됩니다.- 더 나아가서 항상 (h, w) 크기의 필터를 사용해야 하는 점에 대하여
Inception에서 아이디어를 제공합니다. - 행의 방향과 열의 방향으로 필터를 분리하여 필터를 적용하는 방법인데 예를 들어 (3 x 3 x C) 필터를 적용하는 대신 (3 x 1 x C)필터와 (1 X 3 X C) 필터를 적용하는 방법입니다.
- 이렇게 행과 열의 방향으로 필터를 분리하면 파라미터의 갯수를 줄일 수 있습니다. 위의 예에서 정사각형 필터의 파라미터의 수는 9C이지만 분리한 필터의 파라미터 수는 6C가 됩니다.
VGG에서는필터의 크기에 대한 고찰이 있었고Inception에서는정사각형 형태의 필터에 대한 고찰이 있었습니다.MobileNet에서는 입력 데이터에 필터를 적용할 때, 모든 채널을 한번에 계산해서 아웃풋을 만들어야 하는 것에 대한 고찰을 합니다.- 예를 들어, (100(h) x 100(w) x 3(c)) 이미지가 있고 여기에 (3(h) x 3(w) x 3(c)) 필터를 적용하면 3채널 모두에 필터 연산이 적용 되고 그 값들의 합으로 하나의 스칼라 값이 출력되게 됩니다.
MobileNet은 왜 3채널 모두에 연산을 다 해야하지? 라는 의문점에서 시작합니다.
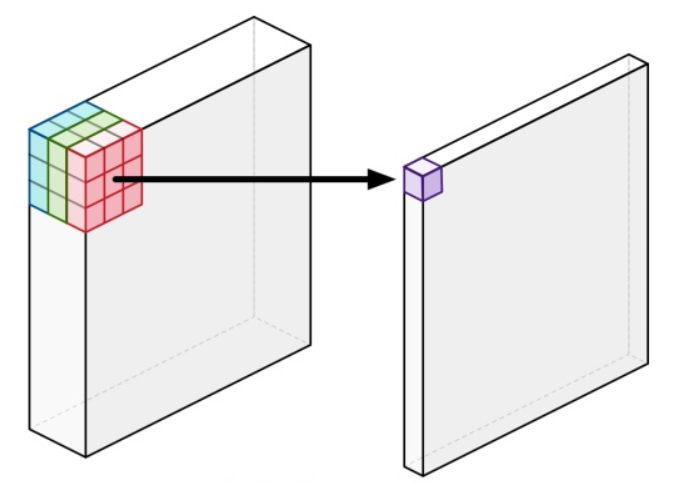
- 위 그림과 같이 연산을 하는 것이 기존의 Convolution 연산입니다.

- 반면 위와 같이 연산을 하는 것이
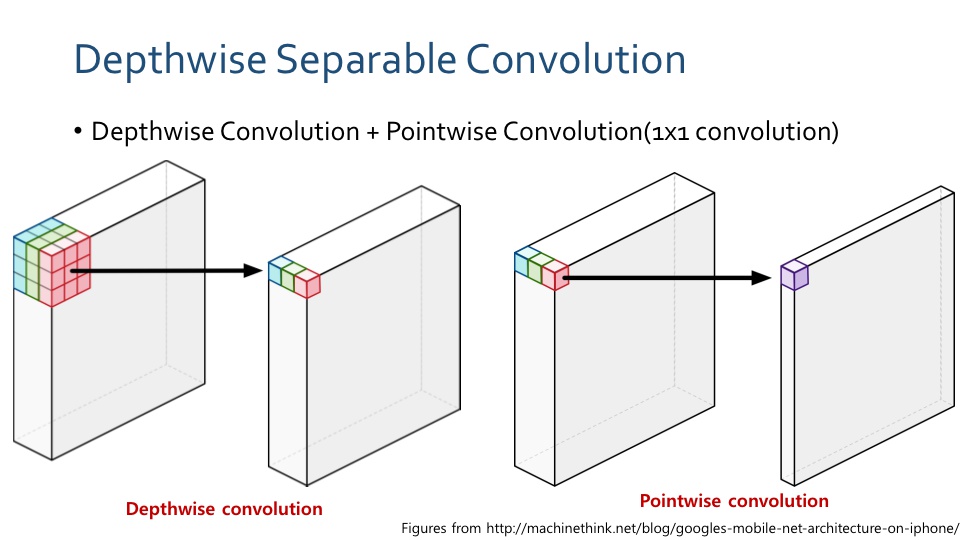
Depthwise Seperable Convolution입니다.- 이 연산은
Depthwise Convolution과Pointwise Convolution으로 나뉩니다.
- 이 연산은
- 결과적으로 이 방법을 사용하는 이유를 먼저 알아보면
연산 속도 증가입니다. - 왼쪽의
Depthwise Convolution을 보면 입력값의 가장 앞쪽 채널인 빨간색 3 x 3 영역만 필터와 연산이 되어 동일한 위치에 스칼라 값으로 출력이 됩니다.- 녹색과 파란색 채널도 각각 필터와 연산이 되어 동일한 위치의 채널에 출력값으로 대응됩니다.
- 이 계산 과정을 기존의 convolution과 비교하면 기존의 연산에서는 한번 필터를 적용하면 출력값을 모두 더하여 한 개의 출력값으로 만든 반면
Depthwise Convolution에서는 채널의 갯수 만큼의 출력값을 가진다는 것입니다. 즉, 채널 방향으로 합치지 않습니다. - 그리고 채널 방향의 연산을 하는 것은
Pointwise Convolution에서 합니다. 즉, 1 x 1 convolution을 적용하는 것입니다.
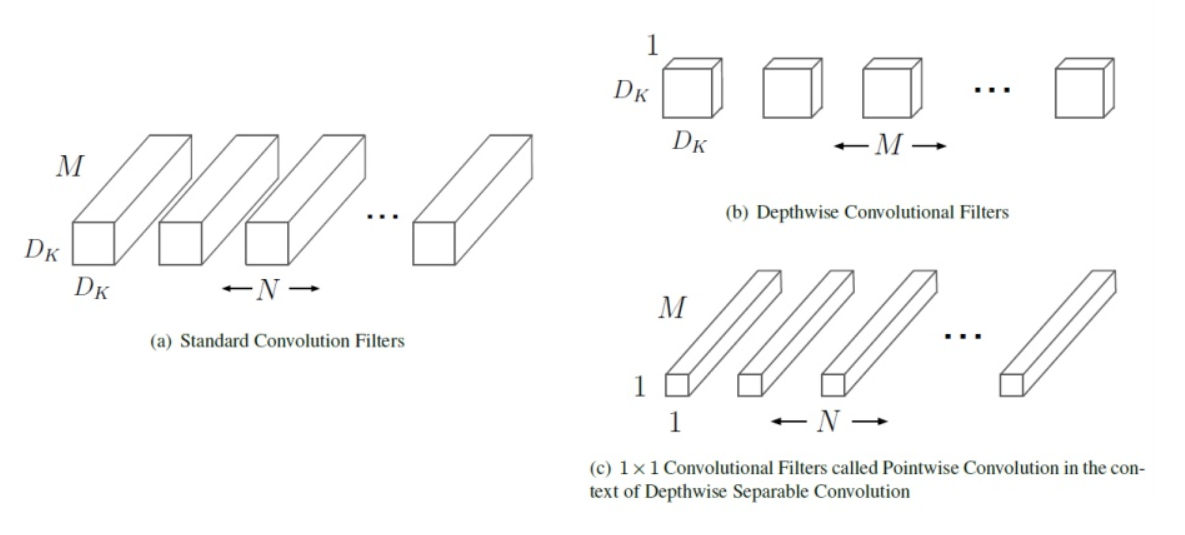
- 위 이미지는 논문에서 사용된 Standard Convolution Filter와 Depthwise Convolution Filter를 비교하기 위해 사용된 이미지입니다.
- 먼저 Standard Convolution Filter에서 \(D_{k}\)는 필터의 height와 width의 크기이고 \(M\)은 필터의 채널 수 그리고 \(N\)은 필터의 갯수가 됩니다. 즉 \(N\)은 아웃풋의 채널수를 이미하기도 합니다.
- 반면 Depthwise Convolution을 보면 (height, width)의 크기가 \(D_{k}\)이고 채널이 1인 \(M\)개의 필터를 이용하여 Depthwise Convolution을 합니다.
- 그리고 그 결과물을 이용하여 1 x 1 필터 N개를 이용하여 Pointwise Convolution을 합니다.
- 결과적으로 이렇게 하면
연산 속도 증가의 장점이 있습니다.
- 얼마나 연산 속도가 증가하는 지 한번 살펴보겠습니다.
- \(D_{K}\) = 필터의 height/width 크기
- \(D_{F}\) = Feature map의 height/width 크기
- \(M\) = 인풋 채널의 크기
- \(N\) = 아웃풋 채널의 크기(필터의 갯수)
- Standard Convolution의 대략적 계산 비용
- \(D_{K} \times D_{K} \times M \times N \times D_{F} \times D_{F}\)
- Depthwise Separable Convolution의 대략적 계산 비용
- \(D_{K} \times D_{K} \times M \times D_{F} \times D_{F} + D_{F} \times D_{F} \times M \times N\)
- 두 Convolution의 계산 비용 차이 (Depthwise Separable Version / Standard Version) - \((D_{K} \times D_{K} \times M \times D_{F} \times D_{F} + D_{F} \times D_{F} \times M \times N) / (D_{K} \times D_{K} \times M \times N \times D_{F} \times D_{F}) = 1/N + 1/D_{K}^{2}\)
- 여기서 \(N\)은 아웃풋 채널의 크기이고 \(D_{K}\)는 필터의 크기인데 \(N\)이 \(D_{K}\) 보다 일반적으로 훨씬 큰 값이므로 반대로 \(1 / D_{K}^{2}\) 값이 되어 \(1 / D_{K}^{2}\) 배 만큼 계산이 줄었다고 보면 됩니다.
- 이 때, \(D_{K}\)는 보통 3이므로 1/9 배 정도 계산량이 감소하였습니다.
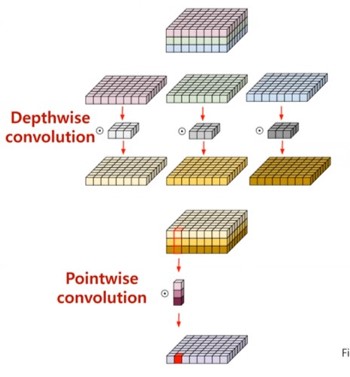
- 마지막으로 정리하면 인풋을 받으면 그 인풋을 depth(채널) 별로 나눈 다음
- 각 채널과 그 채널에 해당하는 3 x 3 필터를 convolution 연산을 해줍니다. 따라서 인풋의 채널수 만큼 3 x 3 필터가 존재합니다.
- convolution 연산을 마친 feature map들을 다시 stack 합니다.
- 이 결과물을 다시 1 x 1 convolution을 해줍니다. 그러면 1채널의 매트릭스가 결과물로 나오게 됩니다.
- 그러면 1 x 1 convolution이 N개이면 N번 연산을 통해 N개의 매트릭스가 결과물로 나오게 되고 그것을 stack하면 volume 형태의 output이 됩니다.
- 이것이
depthwise separable convolution입니다.

- 왼쪽 그림이 일반적인 convolution에서 사용하는 방법이고 오른쪽이 mobilenet에서 사용하는 방법입니다.
- 모바일넷에서는 3 x 3 depthwise convolution → BN → ReLu → 1 x 1 convolution → BN → ReLU 의 순서로 네트워크를 쌓습니다.
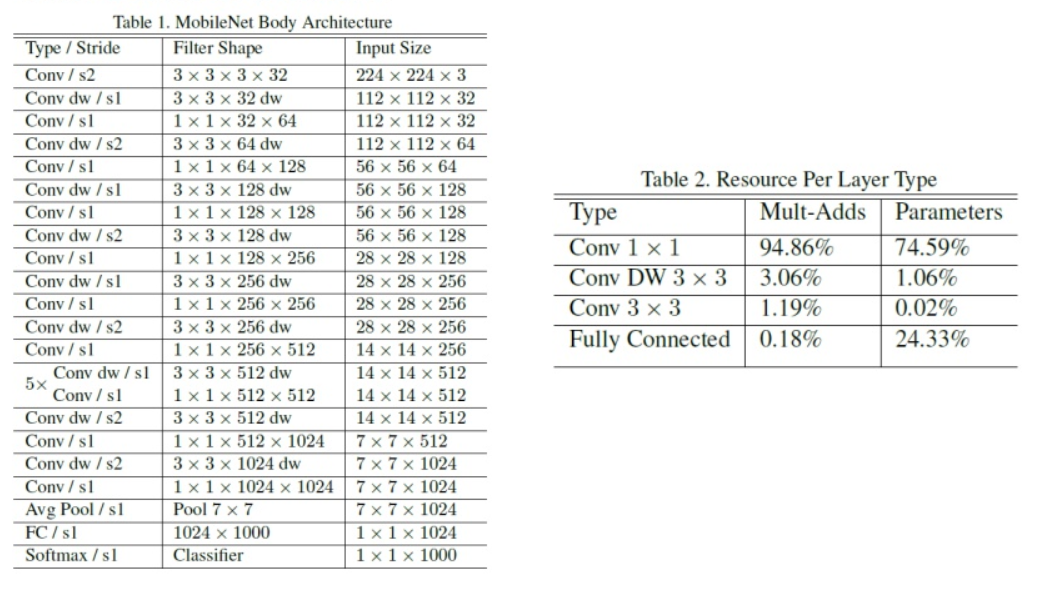
- 위의
Table 1이 전체 네트워크 구조입니다. 여기서dw는 depthwise convolution을 뜻하고s는 stride를 뜻합니다. - 처음에는 인풋 (224, 224, 3) 이미지를 받아서 일반적인 convolution을 거칩니다. 그 다음부터
depthwise convolution과pointwise convolution을 거치게 됩니다. - 마지막에
global average pooling을 하고 그 뒤에FC layer를 추가하여 classification 하는 것으로 구성이 되어있습니다.
- 오른쪽 테이블을 보면 어떤 레이어가 얼만큼의 비중을 차지하는 지 나타냅니다.
- 연산과 파라미터의 대부분이
1 x 1 convolution에 치중이 되어있는 것을 알 수 있습니다. 일반적인 CNN에서는 FC Layer에 연산과 파라미터가 치중되어 있지만depthwise separable구조로 인하여 주요 연산 부분이 변경되었습니다.
- 그 다음으로 논문에서 소개한 개념은
width multiplier와resolution multiplier입니다. - 두 값 모두 기존의 컨셉에서 조금 더 작은 네트워크를 만들기 위해 사용되는
scale값이고 값의 범위는 0 ~ 1입니다. width multiplier는 논문에서 \(\alpha\)로 표현하였고 인풋과 아웃풋의채널에 곱해지는 값입니다.- 논문에서
thinner model을 위한 상수로 사용되었으며채널의 크기를 일정 비율 줄여가면서 실험해 보았습니다.
- 논문에서
- 즉, 채널의 크기를 조정하기 위해 사용되는 값으로 채널의 크기가 \(M\) 이면 \(\alpha M\)으로 표현되어 집니다.
- 논문에서 사용된 \(\alpha\) 값은 1, 0.75, 0.5, 0.25 값입니다.
- 반면
resolution multiplier는 인풋의 height와 width에 곱해지는 상수값입니다. 즉 height와 width가 \(D_{F}\)이면 \(\rho D_{F}\)가 됩니다. - 기본적으로 (224, 224, 3) 이미지를 인풋으로 넣고 실험해본 상수 \(\rho\)는 1, 0.857, 0.714, 0.571로 사이즈 기준으로는 224, 192, 160, 128이 됩니다.
- 이렇게
width, resolution multiplier가 적용되면 계산 비용은 다음과 같이 정의됩니다. 채널에는 \(\alpha\)가 곱해지고 feature map에는 \(\rho\)가 곱해집니다.
[D_{K} \times D_{K} \times \alpha M \times \rho D_{F} \times \rho D_{F} + \alpha M \times \alpha N \times \rho D_{F} \times \rho D_{F}]
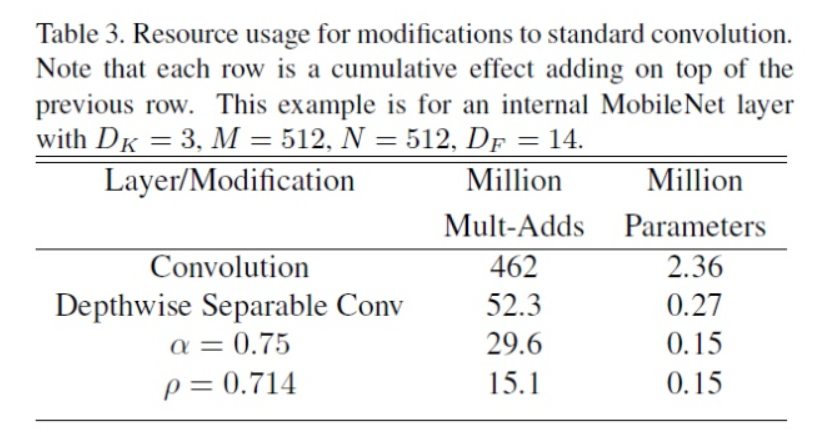
- 여기서 부터는 앞에서 배운 개념의 실험을 통하여
depthwise separable convolution과width, resolution multiplier를 사용하면 효율적으로 설계할 수 있음을 나타냅니다. - 물론 무조건 작게 만든다는게 좋은 것은 아닙니다. 당연히 작게 만든다는 것은 성능과의 어느 정도 트레이드 오프가 일어나기 때문입니다.
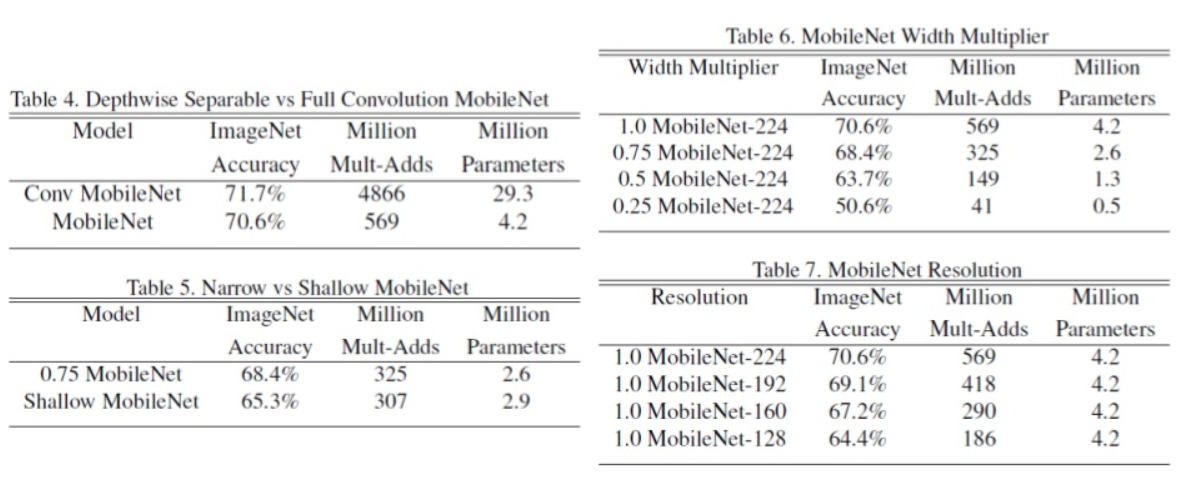
- 먼저 테이블의 열을 보면
Accuracy는 정확도이고Million Multi-Adds는 백만 단위의 곱과 합 연산 수를 뜻합니다. 마지막으로Million Parameters는 파라미터 수를 나타냅니다. Table 4는depthwise separable conv가 기본conv연산보다 정확도는 살짝 떨어지지만 네트워크 경량화에는 상당히 효율적인 것을 보여줍니다.Table 5는narrow한 네트워크 즉, 네트워크의 height, width가 작은 것과shallow한 네트워크 즉, 네트워크의 깊이가 얕은 것 중에 전략을 취한다면 어떤게 나을까? 라는 실험입니다.- 실험의 결과를 보면 shallow한 것 보다
narrow한 것이 더 낫다는 결론을 얻습니다. - 즉, 네트워크 경량화를 해야 한다면 깊이를 줄이기 보다는 네트워크의 height, width를 줄이는 게 더 낫다는 것입니다. 즉, 깊이 있게 쌓는 것이 더 낫다라는 실험입니다.
- 실험의 결과를 보면 shallow한 것 보다
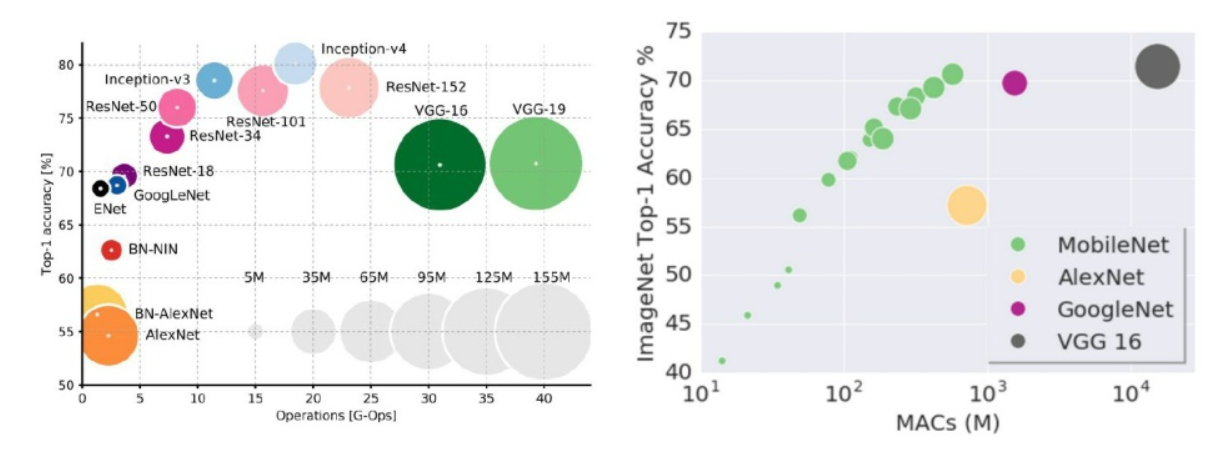
- 위 그림을 보면 가로축은 연산량이라고 보면 되고 (MAC는 Multiply–accumulate operation으로 a = a + (b x c)와 같은 곱과 합의 연산을 말합니다.) 세로축은 정확도이고 원의 크기가 파라미터의 수입니다.
- 모바일넷을 보면 정확도가 GoogLeNet이나 VGG16과 비슷한 수준까지 도달할 수 있고 다만, 이 경우에는 모바일넷의 파라미터 수는 GoogLeNet과 유사할 정도로 많아졌으나 연산량 측면에서는 여전히 앞서는 것을 볼 수 있습니다.
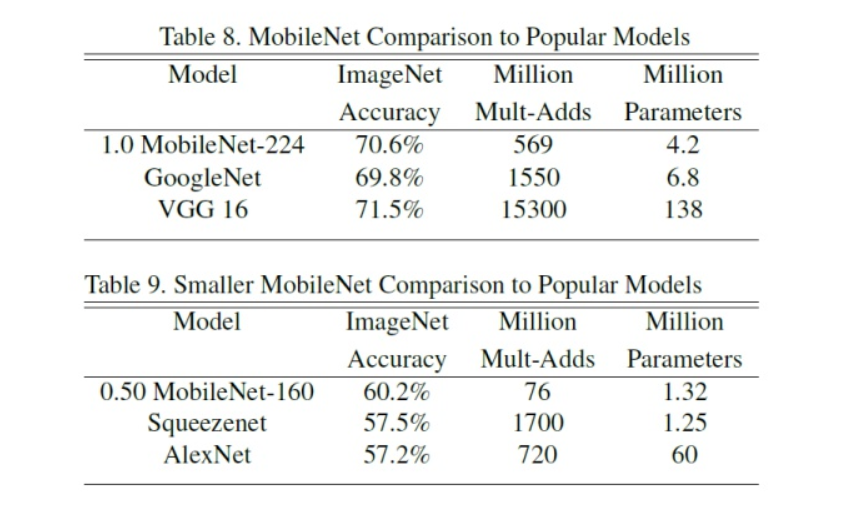
- 다른 유명 모델과 비교하여 표로 정리해 놓은 것을 보면 논문에서는 모바일넷의 성능이 좋다는 것을 피력하고 있습니다.
- 특히 유사한 성격의 경량화 모델인 스퀴즈넷과도 비교를 하였는데, 스퀴즈넷보다 파라미터 수는 약간 많지만 훨씬 적은 연산량으로 더 높은 정확도를 얻을 수 있음을 보여주고 있습니다.
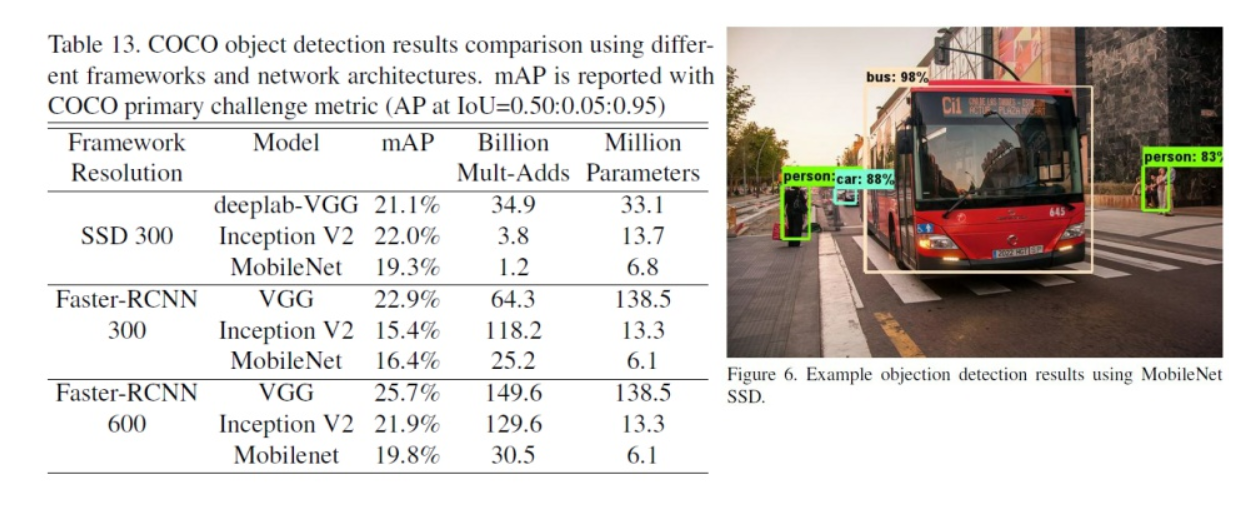
- Object Detection에서의 평가 결과를 찾아보면 (SSD와 Faster R-CNN에서의 숫자 300, 600은 인풋의 크기에 해당) mAP는 다소 떨어지지만 확실히 연산량과 파라미터 수에서 효율적인점이 강점입니다.
- 이런 강점이 모바일 환경에서 Object Detection을 할 수 있는 강점으로 꼽히고 있습니다.
- 여기에 따로 표시하지 않은 다른 실험들도 있으나 그 맥락은 모바일넷이 정확성도 어느정도 보장하면서 연산수와 파라미터수가 작다는 것을 강조하는 논점은 같습니다.
2. Pytorch 코드 리뷰
class MobileNet(nn.Module):
def __init__(self):
super(MobileNet, self).__init__()
def conv_bn(inp, oup, stride):
return nn.Sequential(
nn.Conv2d(inp, oup, 3, stride, 1, bias=False),
nn.BatchNorm2d(oup),
nn.ReLU(inplace=True)
)
def conv_dw(inp, oup, stride):
return nn.Sequential(
nn.Conv2d(inp, inp, 3, stride, 1, groups=inp, bias=False),
nn.BatchNorm2d(inp),
nn.ReLU(inplace=True),
nn.Conv2d(inp, oup, 1, 1, 0, bias=False),
nn.BatchNorm2d(oup),
nn.ReLU(inplace=True),
)
self.model = nn.Sequential(
conv_bn( 3, 32, 2),
conv_dw( 32, 64, 1),
conv_dw( 64, 128, 2),
conv_dw(128, 128, 1),
conv_dw(128, 256, 2),
conv_dw(256, 256, 1),
conv_dw(256, 512, 2),
conv_dw(512, 512, 1),
conv_dw(512, 512, 1),
conv_dw(512, 512, 1),
conv_dw(512, 512, 1),
conv_dw(512, 512, 1),
conv_dw(512, 1024, 2),
conv_dw(1024, 1024, 1),
nn.AvgPool2d(7),
)
self.fc = nn.Linear(1024, 1000)
def forward(self, x):
x = self.model(x)
x = x.view(-1, 1024)
x = self.fc(x)
return x