
Softmax와 Negative Log Likelihood Loss 및 Binary Cross Entropy
2020, Jan 07
목차
-
Softmax
-
Negative Log-Likelihood (NLL)
-
Negative Log Likelihood에 대한 Softmax 함수의 미분
-
Pytorch에서 사용 방법
-
Softmax의 overflow 방지
-
2차원 Softmax 함수
-
확률 분포를 학습하기 위한 binary_cross_entropy 함수
- 이번 글에서는
softmax와Negative Log-Likelihood를 사용하는NLL Loss에 대하여 설명해 보겠습니다.
Softmax
softmax는 보통 뉴럴 네트워크의 출력 부분 layer에 위치하고 있으며 사용 목적은 multi-class classification과 같은 문제에서 최총 출력을 할 때에 출력값을 0과 1사이의 확률값과 같이 나타내기 위해 사용됩니다.
- \[S(f_{y_{i}}) = \frac{e^{f_{ y_{i} } }}{\sum_{j}e^{f_{j}}}\]
- 위 식과 같이 모든 출력되는 모든 아웃풋을
exp()를 이용하여 양수화 하고 normalization 작업을 거치면 모든 값이 0과 1 사이의 값이 될 뿐 아니라 총 합이 1이 되어 확률 처럼 다룰 수 있게 됩니다. - 아래와 같이 3개의 이미지 고양이, 말, 개를 이용하여 한번 살펴보도록 하겠습니다.
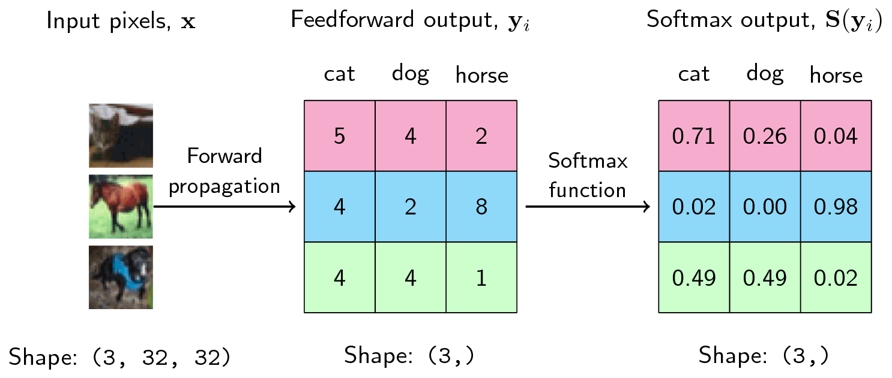
- 먼저 고양이 이미지 입력을 넣었을 때, 출력은 분홍색, 말은 파란색, 개는 초록색에 해당합니다. 가운데 행렬이 출력값에 해당하며 행렬의 첫번째 열은 고양이, 두번째 열은 개, 세번째 열은 말에 해당하며 가장 큰 값을 가지는 클래스가 선택됩니다.
- 첫번째 분홍색을 살펴보면 고양이가 열의 값이 5로 가장 크므로 고양이가 선택됩니다. 파란색을 살펴보면 세번째 열인 말이 가장 큰 값인 8을 가지므로 말이 선택됩니다.
- 초록색을 살펴보면 첫번째 열과 두번째 열의 값이 모두 4로 같으므로 어떤 것을 선택해야 할 지 애매한 상황에 놓이게 됩니다.
- 위와 같은 방법으로 가장 값이 큰 값을 선택해도 되지만 확률적으로 표현하면 좀 더 직관적으로 살펴볼 수 있습니다. 이 때,
softmax계산을 적용하여 가장 오른쪽 행렬과 같이 나타낼 수 있습니다. softmax 연산은 대소 크기를 바꾸지 않으므로 앞에서 선택된 것과 동일한 열이 선택되며 초록색을 살펴 보더라도 첫번째 열과 두번째 열의 값이 0.49로 같음을 확인할 수 있습니다. - 이와 같은 방법을 통하여
softmax의 출력은 뉴럴 네트워크의confidence와 같은 역할을 할 수 있습니다.
Negative Log-Likelihood (NLL)
- 앞에서 다룬
softmax와 더불어서NLL을 이용하여 딥러닝의Loss를 만들 수 있습니다. 적용하는 방법은 간단하며 구현 방법에 따라 다음 두가지 방법으로 나뉩니다. 방법은 ①argmax를 취하는 방법과 ②모든 logit에 적용하는 방법이 있습니다. - ①
argmax를 취하는 방법 : 어떤 입력에 대한sofrmax출력 중 가장 큰 값을 다음 식에 적용하면 됩니다. \(y\)는 softamx 출력값 중 가장 큰 값입니다.
- \[L(\mathbf{y}) = -\log(\mathbf{y})\]
- 위 식에서 log 함수와 음의 부호를 사용함으로써 softmax의 출력이 낮은 값은 \(-log(y)\) 값이 크도록 만들 수 있고 softmax의 출력이 높은 값은 \(-log(y)\)의 값이 0에 가깝도록 만듭니다.
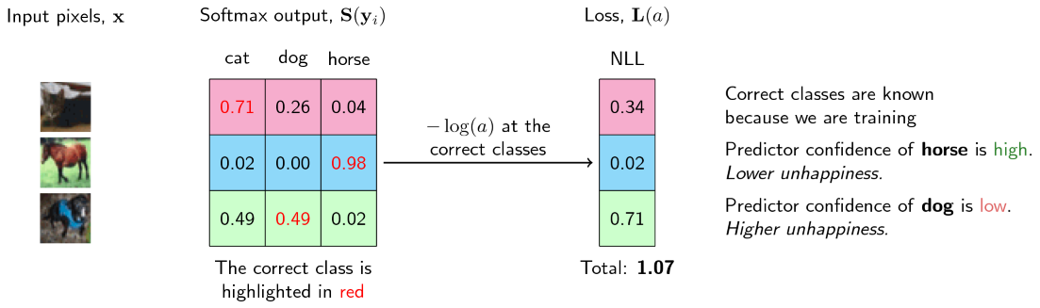
- 정답 클래스의 softmax 출력이 높은 값을 가진다면 출력이 정확한 것이므로 \(-\log(\mathbf{y})\)가 매우 작아지게 됩니다. 마치 Loss가 작아지는 것과 같습니다.
- 정답 클래스의 softmax 출력이 낮다면 \(-\log(\mathbf{y})\)는 큰 값을 가집니다. 즉, 출력이 정확하지 못한 부분에 대해서는 높은 Loss를 가지는 것 처럼 나타낼 수 있습니다.
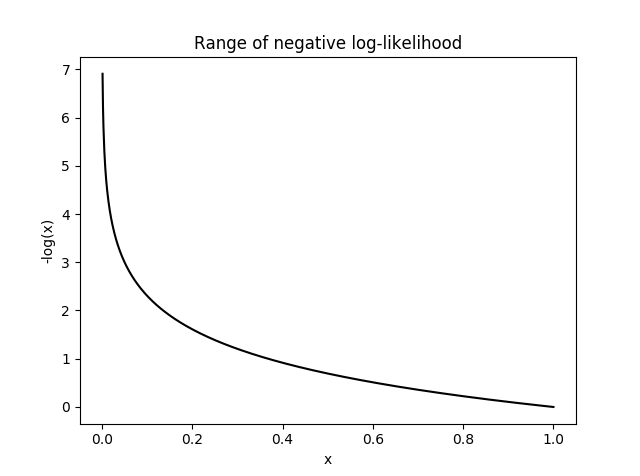
- 따라서 위 그래프와 같이 softmax 출력에 대한 \(-\log(\mathbf{y})\)는 Loss 처럼 나타낼 수 있습니다.
- ②
모든 logit에 적용하는 방법 : 이 방법은 ①에서 다룬argmax부분을 없애고 softmax를 취하고 나온 모든logit에 대하여loss를 구하는 방법입니다.

- 위 그림과 같이 정답에 해당하는 클래스에는
-log(a)를 취하고 정답이 아닌 클래스에는-log(1-a)를 취합니다. - 정답 클래스의 경우 softmax의 결과가 1에 가까워야 하고 1에 가까울수록
-log(a)는 0에 가까워지므로 loss가 줄어들게 됩니다. - 반면 정답이 아닌 클래스의 경우 softmax의 결과가 0에 가까워야 하고 0에 가까울수록
-log(1-a)는 0에 가까워지므로 loss가 줄어들게 됩니다. - 최종적으로 계산된 모든
NLL Loss에 대하여sum또는mean연산을 취하면 Loss가 하나의 스칼라 값으로 도출되게 됩니다. eps를 적용하는 이유는 극단적으로 Loss값이 무한대에 가까워져서NaN이 생기는 것을 방지하기 위함입니다.
- 참고로
Pytorch에서 사용되는 Loss 방법은 ②모든 logit에 적용하는 방법이므로 이를 참조하여 Custom한 Loss를 설계하는데 참조하시면 됩니다.
Negative Log Likelihood에 대한 Softmax 함수의 미분
- Loss function을 적용하기 위해서는 미분이 가능해야 하므로 Negative Log Likelihood에 대한 Softmax 함수의 미분을 해보도록 하겠습니다. 먼저 \(f\)를 딥 러닝 네트워크의 출력인 클래스 별 최종 score를 저장한 벡터로 정의합니다.
- 이 때, \(f_{k}\)는 전체 클래스의 갯수가 \(j\)인 벡터에서 \(k\)번째 클래스의 score로 정의 됩니다.
- 먼저 softmax 함수는 다음과 같이 정의 할 수 있습니다.
- \[p_k = \dfrac{e^{f_k}}{\sum_{j} e^{f_j}}\]
- 다음으로 softmax 함수의 출력을 받는 NLL을 다음과 같이 정의 할 수 있습니다.
- \[L_i = -log(p_{y_{i}})\]
- 위 식에 대하여 \(\dfrac{\partial L_i}{\partial f_k}\) 와 같이 미분한 결과를 통하여 backpropagation을 할 때, Loss가 어떻게 반영되는 지 알 수 있습니다.
- \[\dfrac{\partial L_i}{\partial f_k} = \dfrac{\partial L_i}{\partial p_k} \dfrac{\partial p_k}{\partial f_k}\]
- 따라서 위 식과 같이 Loss의 \(f_{k}\)에 대한 미분값을 알아보기 위하여 \(\dfrac{\partial L_i}{\partial p_k}\)를 먼저 풀고 그 다음 \(\dfrac{\partial p_{y_i}}{\partial f_k}\) 결과를 연달아서 계산해 보도록 하겠습니다.
- 먼저 \(\dfrac{\partial L_i}{\partial p_k}\) 의 계산 결과는 간단하게 구할 수 있습니다.
- \[\dfrac{\partial L_i}{\partial p_k} = -\dfrac{1}{p_k}\]
- 그 다음으로 두번째 term을 미분하기 위하여 다음과 같이 분수 미분을 적용하려고 합니다.
- \[\dfrac{f(x)}{g(x)} = \dfrac{g(x) \mathbf{D} f(x) - f(x) \mathbf{D} g(x)}{g(x)^2}\]
- 식을 단순하 하기 위하여 \(\sum_{j} e^{f_j} = \Sigma\)로 치환하고 다음과 같이 식을 전개합니다.
- \[\begin{eqnarray} \dfrac{\partial p_k}{\partial f_k} &=& \dfrac{\partial}{\partial f_k} \left(\dfrac{e^{f_k}}{\sum_{j} e^{f_j}}\right) \\ &=& \dfrac{\Sigma \mathbf{D} e^{f_k} - e^{f_k} \mathbf{D} \Sigma}{\Sigma^2} \\ &=& \dfrac{e^{f_k}(\Sigma - e^{f_k})}{\Sigma^2} \end{eqnarray}\]
- 다음 스텝으로 위 식에서 \(\mathbf{D}\Sigma= \mathbf{D} \sum_{j} e^{f_j} = e^{f_k}\) 를 적용합니다. 왜냐하면 \(k\)번째 항에 대하여 미분을 할 때에는 \(k\) 번째 항이 아닌 항은 모두 0이 되고 \(k\)번째 항은 \(e^{f_k}\)가 되기 때문입니다.
- \[\begin{eqnarray} \dfrac{\partial p_k}{\partial f_k} &=& \dfrac{e^{f_k}(\Sigma - e^{f_k})}{\Sigma^2} \\ &=& \dfrac{e^{f_k}}{\Sigma} \dfrac{\Sigma - e^{f_k}}{\Sigma} \\ &=& p_k * (1-p_k) \end{eqnarray}\]
- 따라서 backpropagation 결과를 모두 합치면 다음과 같이 미분할 수 있습니다.
- \[\begin{eqnarray} \dfrac{\partial L_i}{\partial f_k} &=& \dfrac{\partial L_i}{\partial p_k} \dfrac{\partial p_k}{\partial f_k} \\ &=& -\dfrac{1}{p_k} (p_k * (1-p_k)) \\ &=& (p_k - 1) \end{eqnarray}\]
NLL Loss미분의 결과가 \(p_{k} - 1\)이 됨을 통하여 softmax와 negative log likelihood를 조합하여 Loss로 사용할 수 있음을 확인하였습니다.
Pytorch에서 사용 방법
- 위에서 설명한
NLLLoss는 Pytorch에 기본적으로 적용이 되어 있으므로 다음 링크의 함수를 사용하면 됩니다. NLLLoss에서 사용하는 파라미터 중 가장 중요한 파라미터는weight입니다.NLLLoss의 장점 중 하나인weight는 클래스 불균형 문제를 개선하기 위하여 수동으로 weight 별 학습 비중의 스케일을 조정하기 위해 사용됩니다.- 예를 들어 클래스의 갯수가 3개이고 클래스 별 데이터의 갯수가 (10, 50, 100) 이라면 weight는 데이터 갯수와 역의 관계로 대입을 해주어야 합니다. 예를 들면 (1, 0.2, 0.1)와 같이 weight를 설정할 수도 있고 (1/10, 1/50, 1/100)과 같이 사용할 수도 있습니다. 핵심은 적은 갯수의 데이터에 해당하는 클래스에 높은 weight를 주어 학습 양을 늘리는 데 있습니다.
import torch.nn as nn
import nn.functional as F
loss = nn.NLLLoss(weight)
# output shape : (Batch Size, C, d1, d2, ...)
loss(F.log_softmax(output, 1), targets)
Softmax의 overflow 방지
- 앞에서 다룬
softmax를 실제 구현해서 사용한다면exp함수를 사용할 때, 너무 큰 수가 지수 승으로 입력이 되면 overflow가 발생하게 됩니다. 따라서 아래와 같이 개선된 버전의 수식을 사용하는 것이 일반적입니다.
- \[y_{k} = \frac{\text{exp}(a_{k})}{\sum_{i=1}^{n} \text{exp}(a_{i})} = \frac{C \text{exp}(a_{k})}{C \sum_{i=1}^{n} \text{exp}(a_{i})}\]
- \[= \frac{\text{exp}(a_{k} + \log{(C)})}{\sum_{i=1}^{n} \text{exp}(a_{i} + \log{(C)})}\]
- \[= \frac{\text{exp}(a_{k} + C')}{\sum_{i=1}^{n} \text{exp}(a_{i} + C')}\]
- 즉, 위 식을 정리하면 \(C\) 라는 값을 기존 softmax 식의 분모 분자에 곱한 후 \(C\) 를
exp안으로 옮겨log(C)로 변경 후 최종적으로C'로 치환하였습니다. - 즉, 어떤 정수를
exp에 더하더라도 결과를 유지한다는 뜻이 됩니다. 이 성질을 이용하여 overflow를 방지해보겠습니다. - 아래 코드에서 구현하는 방법은 값 중의 최댓값을 전체 값에 빼준 다음에 softmax를 취해주게 되면 overflow를 방지할 수 있는 내용입니다.
a = np.array([1010, 1000, 990])
print(np.exp(a) / np.sum( np.exp(a) ))
# array([nan, nan, nan])
- 위 코드 결과와 같이 overflow 방지를 위해 아래와 같이 사용합니다.
c = np.max(a)
print(a - c)
# array([ 0, -10, -20])
print(np.exp(a - c) / np.sum( np.exp(a - c) ))
# array([9.99954600e-01, 4.53978686e-05, 2.06106005e-09])
- 기존 코드에서는 overflow가 발생하였지만, 최댓값을 뺀 다음에 사용하면 overflow가 발생하지 않습니다.
- 위 트릭을 적용하여 softmax 함수를 다시 정의하면 아래와 같습니다.
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
2차원 이상의 Softmax 함수
- 앞에서 선언한
softmax함수는 1차원 배열을 대상으로 적용할 수 있는 함수입니다. 2차원 이상의 배열에 대하여 softmax를 적용하려면 어떻게 해야 하는 지 살펴보겠습니다.
# 최종 softmax
def softmax(a):
if a.ndim >= 2:
# axis 1에 대하여 최댓값을 구함
c = np.max(a, axis=1, keepdims=True )
# 각 값에 axis 1 기준으로 최댓값을 뺌
exp_a = np.exp(a - c)
# exp 적용
sum_exp_a = np.sum( exp_a, axis=1, keepdims=True )
else:
c = np.max(a)
exp_a = np.exp(a - c)
sum_exp_a = np.sum(exp_a)
return exp_a / sum_exp_a
a = np.array([ [0.3, 2.9, 4.0],
[0.5, 1.1, 8.0],
[0.9, 12.9, 34.0] ])
b = np.array([0.3, 2.9, 4.0])
print( 'softmax(a)\n', softmax(a))
# softmax(a)
# [[1.82112733e-02 2.45191813e-01 7.36596914e-01]
# [5.52222423e-04 1.00621486e-03 9.98441563e-01]
# [4.21553451e-15 6.86098439e-10 9.99999999e-01]]
print('softmax(b)\n', softmax(b))
# softmax(b)
# [0.01821127 0.24519181 0.73659691]
print('sum( softmax(a) )\n', np.sum( softmax(a), axis=1, keepdims=True))
# sum( softmax(a) )
# [[1.]
# [1.]
# [1.]]
print('sum( softmax(b) )\n', np.sum(softmax(b)))
# sum( softmax(b) )
# 1.0
확률 분포를 학습하기 위한 binary_cross_entropy 함수
- 아래는
F.binary_cross_entorpy함수의 구현 방식의 메커니즘입니다. 파이썬 코드 형태로 메커니즘이 잘 설명되어 있고 실제 출력은F.binary_cross_entorpy와 같습니다.
def binary_cross_entropy(pred, y):
log_pred = torch.clamp(torch.log(pred), -100, 100)
log_pred_rev = torch.clamp(torch.log(1-pred), -100, 100)
return -(log_pred*y + (1-y)*log_pred_rev).sum()
a = torch.linspace(0, 1, 10)
w = np.array([F.binary_cross_entropy(x,torch.tensor(0.2)).item() for x in a])
q = np.array([binary_cross_entropy(x,torch.tensor(0.2)).item() for x in a])
print(w)
print(q)