딥러닝 학습 시 사용되는 optimizer

출처 : 밑바닥부터 배우는 딥러닝
이번 글에서는 딥러닝 시 사용되는 optimizer들에 대하여 살펴보도록 하겠습니다.

확률적 경사 하강법(SGD)

가장 간단한 방법 중의 하나인 SGD(Stochastic Gradient Descent) 방법부터 살펴보도록 하겠습니다.
먼저 수식은 \(W = W - \eta \frac{\partial L}{\partial W}\) 입니다.
- 여기에서 \(W\)는 갱신할 가중치 매개변수이고 \(\frac{\partial L}{\partial W}\) 는 \(W\)에 대한 손실 함수의 기울기 입니다.
- 그리고 \(\eta\)는 학습률을 의미하는 데 0.01 또는 0.001과 같은 값을 미리 정하여 사용합니다.
먼저 SGD를 Numpy를 이용하여 구현해 보도록 하겠습니다.

class SGD:
    
    def __init__(self, lr = 0.01):
        self.lr = lr
        
    def update(selfself, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]

초기화 때 받은 변수 lr은 learning rate를 뜻합니다.
update(params, grads)는 SGD에서 반복해서 호출됩니다. params와 grads는 dictionary로 params[‘W1’], grads[‘W1’]\ 과 같이 가중치 매개변수와 기울기를 저장하고 있습니다.

SGD의 개념은 아주 간단하지만 비효율적이라는 단점일 발생 할 수 있습니다.
만약 \(f(x, y) = \frac{1}{20}x^{2} + y^{2}\) 과 같은 식이 있고 최솟값을 구해야 한다면 어떻게 구할 수 있을까요?
SGD 방법을 사용한다면 경사를 따라 내려올 것입니다.

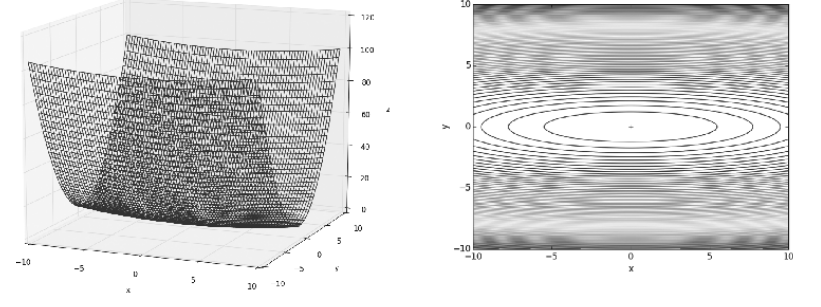
하지만 위 그림과 같이 y축으로는 경사가 있어서 쉽게 내려올 수 있지만 x축으로는 너무 완만하여 경사를 따라 내려오기가 어렵습니다.

즉, 위 식이 최솟값을 가지려면 x=0, y=0 을 가져야 하지만 위 경사도와 기울기를 보면 y축은 0으로 도달할 수 있더라고 x축은 0으로 도달하기가 어려울 수 있습니다.

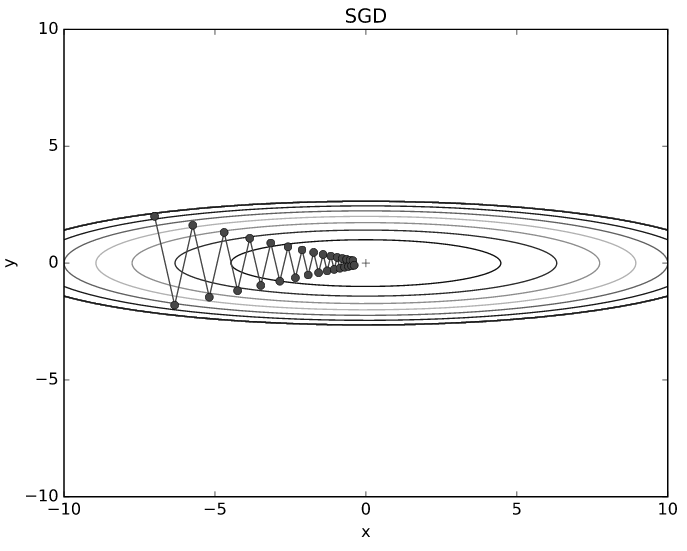
만약 식을 (x=-7, y=2)에서 시작한다면 위와 같이 지그재그로 이동하면서 최솟값에 다가갈 것입니다.
즉, 무작정 경사가 진 곳으로만 따라간다면 솔루션을 효율적인 방법으로 찾는다고 보장할 수 없고 비효율적일 것입니다.

모멘텀

모멘텀은 운동량을 나타내는 뜻으로 물리에서 가져온 개념입니다.
모멘텀의 수식은 다음과 같습니다.
- 　\(v = \alpha v - \eta \frac{\partial L }{\partial W}\)
- 　\(W = W + v\)
위 식을 살펴보면 모멘텀은 SGD와 달라진 점은 \(\alpha v\) 입니다.
여기서 \(v\) 라는 변수는 물리에서 말하는 속도 입니다.

위 식의 \(\alpha v\)는 위 그림과 같이 기울기 방향으로 힘을 받아 물체가 가속된다는 것을 뜻합니다.
이 때 사용되는 \(\alpha\)의 값은 1보다 작은 값으로 시간이 지나면 서서히 \(v\)의 값이 줄어들게 설계됩니다.
- 이것은 물리에서의 지면 마찰이나 공기저항에 해당합니다.
모멘텀을 코드로 나타내면 다음과 같습니다.

class Momentum:
    def __init__(self, lr = 0.01, momentum = 0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
                
        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]

인스턴스 변수 v는 물체의 속도입니다. v는 초기화 때는 아무 값도 담지 않고, 대신 update()가 처음 호출될 때, 매개변수와 같은 구조의 데이터를 딕셔너리 변수로 저장합니다.

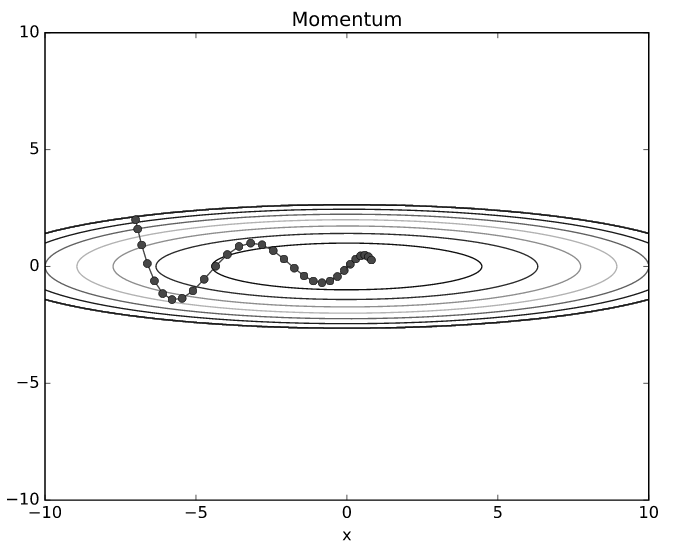
모멘텀의 업데이트 경로를 보면 SGD보다 지그재그 량이 덜 한것을 알 수 있습니다.
x축의 힘은 작긴 하지만 방향은 변하지 않아서 한 방향으로 일정하게 가속하기 때문입니다.
반대로 y축의 힘은 크지만 위아래로 번갈아 받아서 y축 방향의 속도는 안정적이지 않습니다.
전체적으로는 SGD보다 x축 방향으로 빠르게 다가가 지그재그로 움직입니다.

확률적 경사 하강법(SGD)

모멘텀

AdaGrad