Transformer와 Nerf에서의 Positional Encoding의 의미와 사용 목적

딥러닝 Concept 관련 글 목차

참조 : https://towardsdatascience.com/master-positional-encoding-part-i-63c05d90a0c3
참조 : https://www.blossominkyung.com/deeplearning/transfomer-positional-encoding
참조 : https://velog.io/@gibonki77/DLmathPE
참조 : https://machinelearningmastery.com/a-gentle-introduction-to-positional-encoding-in-transformer-models-part-1/
이번 글에서는 Transformer에서 Input에 같이 사용되는 Positional Encoding의 의미와 사용 목적을 간략히 정리하고자 합니다.

Positional Encoding의 필요성

Transformer 이전에는 RNN 구조의 LSTM과 같은 모델을 사용하여 순차적으로 입력되는 데이터 (ex. 문장)를 처리하였습니다. 이 구조에서는 Input에 입력되는 순서대로 RNN 모델 내에서 처리가 되었습니다. 즉, 앞의 데이터 연산이 끝나야 뒤의 연산을 진행할 수 있었습니다.
데이터가 한번에 1개씩 처리되기 때문에 연산 속도가 매우 느리다는 문제점이 있었습니다. 하지만 Transformer의 경우 입력되는 데이터를 순차적으로 처리하지 않고 한번에 병렬로 처리한다는 특징이 있습니다.
이와 같은 병렬 처리로 인한 장점이 있는 반면 데이터를 병렬 처리하면서 데이터가 입력된 순서에 대한 정보가 사라지는 문제가 발생하게 됩니다.
이 문제를 개선하기 위하여 Positional Encoding이라는 개념을 도입하여 말 그대로 위치 정보를 Encoding 하는 역할을 하게 됩니다.
입력값에 위치 정보를 추가하는 방법에는 다양한 방법이 있으나 Transformer에 사용된 Positional Encoding 방법이 범용적으로 많이 사용됩니다. 왜냐하면 연속적으로 입력되는 데이터에 대하여 효과적으로 위치정보를 줄 수 있는 방법이기 때문입니다.
반대로 말하면 Naive한 방법으로 데이터의 위치 정보를 추가하게 되면 몇가지 문제가 발생할 수 있습니다.

Positional Encoding의 필요 조건

효과적인 Positional Encoding을 생성하기 위하여 어떤 필요 조건들이 있는 지 살펴보도록 하곘습니다.
먼저 Positional Encoding은 입력값에 위치 정보를 더하는 방식으로 계산됩니다.

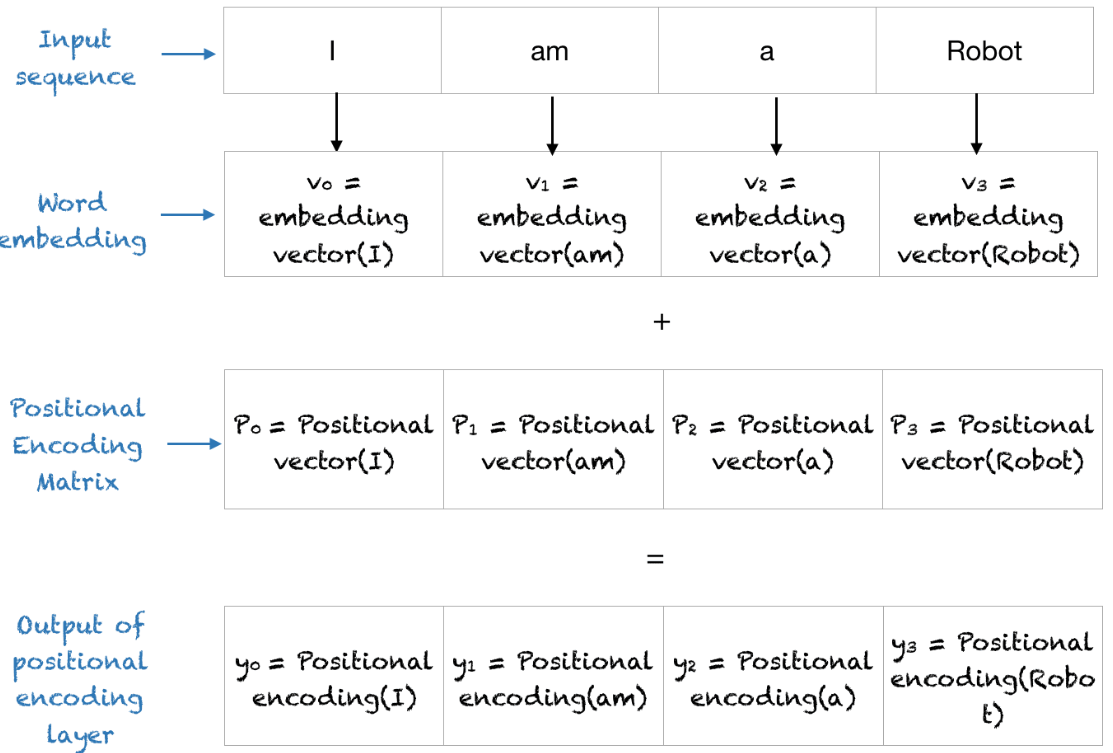
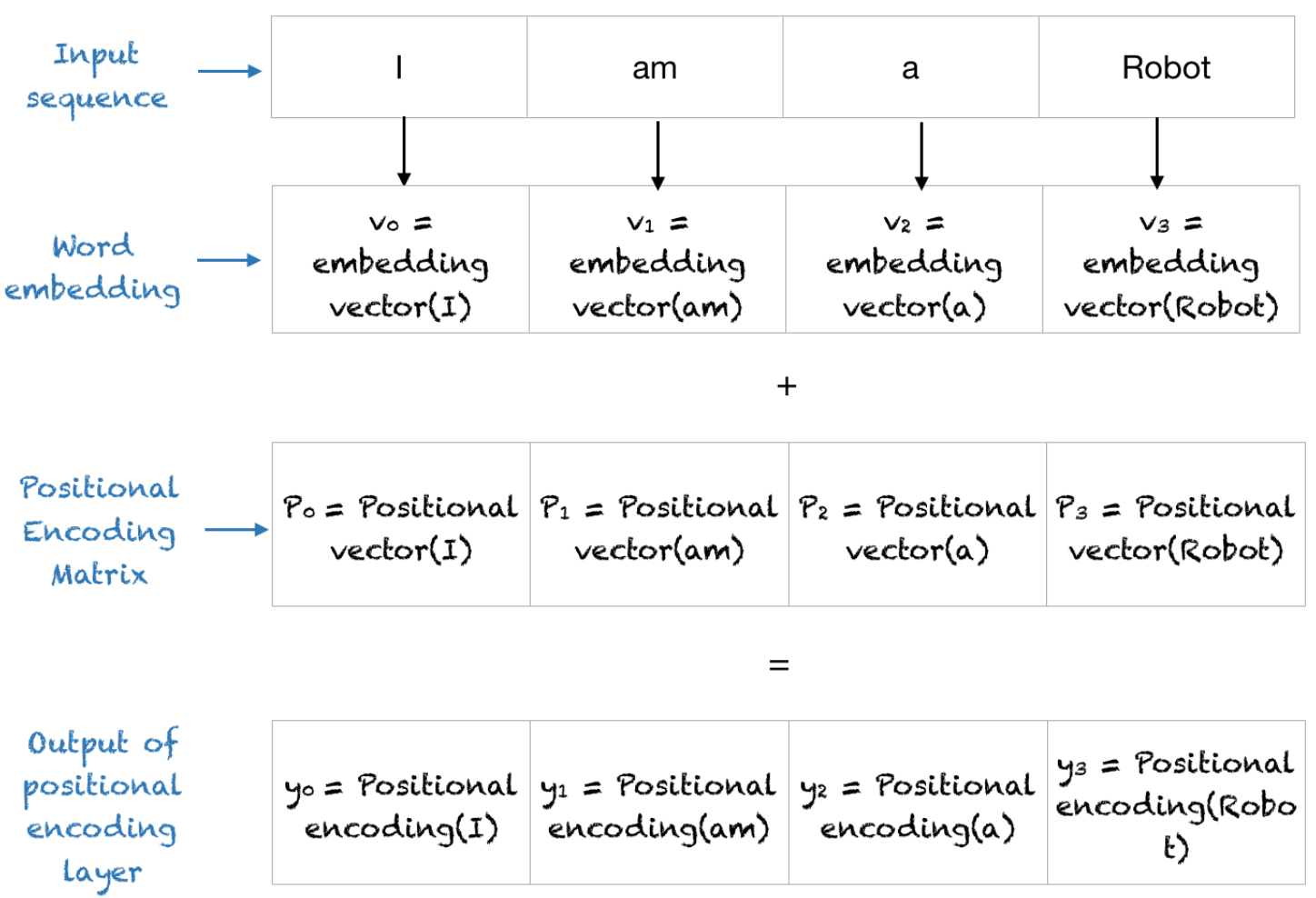
위 그림처럼 4개의 단어 데이터가 입력될 때, 4개의 Positional Encoding이 입력 데이터를 임베딩한 결과에 더해집니다.
즉, 입력 데이터와 같은 사이즈의 Positional Encoding이 생성되어야 하며 이 값이 각 데이터의 순서를 의미해야 합니다. Positional Encoding 값이 concat이 되지 않고 더해지는 이유는 concat에 의한 과다한 메모리 낭비, 런타임 증가 등이 있을 수 있으며 차원이 증가한다는 문제점도 발생할 수 있기 때문입니다. 특히, Transformer 구조가 GPU를 많이 필요로 하는 만큼 concat을 하지 않고 덧셈을 하게 됩니다.
concat을 하였을 때에는 입력 데이터의 값을 변경시키지 않기 때문에 데이터의 의미와 위치의 의미가 전혀 다른 공간에 생성되어 서로 악영향을 주지 않을 수 있는 장점이 있습니다. 하지만 앞에서 언급한 문제가 있으므로 결론적으로 더하는 방식을 사용하고 Positional Encoding을 할 때, 위치 정보가 입력 정보를 왜곡시키지 않도록 만들어야 합니다.

이와 같은 배경에서 Positional Encoding이 만족해야 하는 필요 조건들을 나열하면 아래와 같습니다.
① 각 위치값은 시퀀스의 길이나 입력값에 관계없이 동일한 위치값을 가져야 합니다. 즉, 시퀀스 데이터가 변경되더라도 위치 임베딩은 동일하게 유지되어 입력값에 대한 순서 정보를 유지할 수 있어야 합니다.
② 모든 위치값이 입력값에 비해 너무 크면 안됩니다. 위치값이 너무 커져버리면 데이터가 가지는 의미값이 상대적으로 작아지게 되므로 입력값이 왜곡되게 됩니다.
③ Positional Encoding의 값이 빠르게 증가되면 안됩니다. Positional Encoding의 값이 너무 빨리 커지게 되면 증가된 위치에 weight가 커지게 되고 gradient vanishing 또는 gradient explosiong 등 학습이 불안정하게 진행될 수 있습니다.
④ 위치 차이에 의한 Positional Encoding값의 차이를 거리로 이용할 수 있어야 합니다. 예를 들어 0번째, 1번째 Positional Encoding 값의 차이가 1번째, 2번째 Positional Encoding값의 차이와 유사해야 합니다. 그렇게 되어야 위치 차이 1만큼 났을 때, Positional Encoding 또한 같은 거리 만큼 차이 나는 것을 인식할 수 있기 때문입니다. 따라서 등간격으로 배열된 부드러운 곡선 형태를 사용합니다.
⑤ Positional Encoding 값은 위치에 따라 서로 다른 값을 가져야 합니다. 위치 정보를 나타내는 만큼 서로 다른 값을 나타내어야 학습할 때 의미 있게 사용할 수 있습니다.

가장 간단한 방법으로 아래와 같이 위치가 증가할 수록 Positional Encoding의 값 또한 증가하도록 만들 수 있습니다.

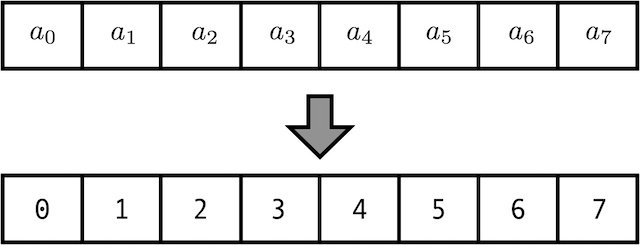
하지만 위 예시처럼 구현한다면 앞의 ② 모든 위치값이 입력값에 비해 너무 크면 안된다는 것과 ③ Positional Encoding의 값이 빠르게 증가되면 안된다는 것에 위배됩니다.
만약 값이 크게 증가하는 것을 방지하기 위하여 아래와 같이 정규화를 하면 어떻게 될까요?

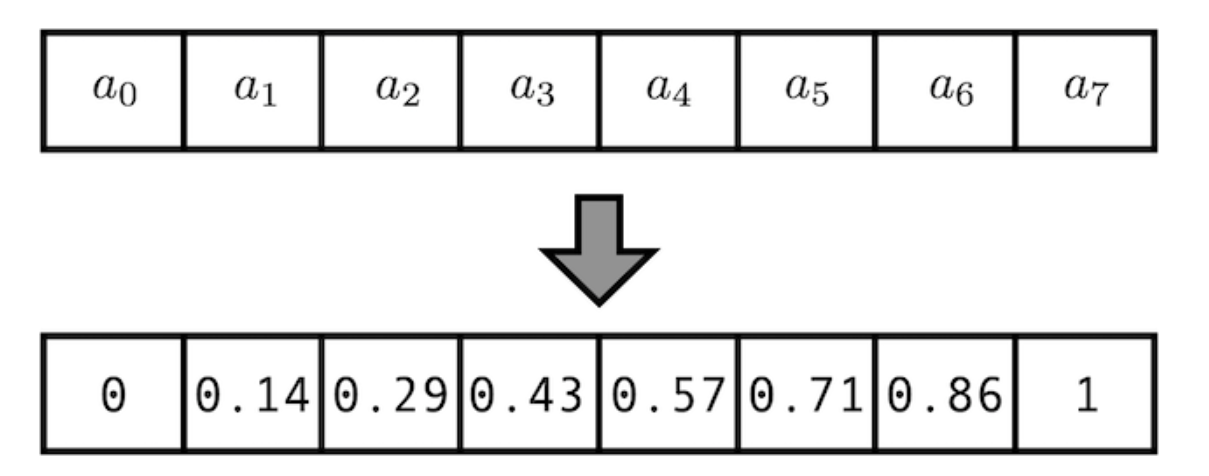
이 경우에는 ① 각 위치값은 시퀀스의 길이나 입력값에 관계없이 동일한 위치값을 가져야한다는 조건을 위배합니다. 위 예시의 경우 입력 데이터의 길이에 따라 정규화 해주는 값이 (max_len -1)로 정해지기 때문에 고정된 위치값을 가질 수 없습니다.
앞의 2가지 케이스의 문제를 개선하기 위하여 Positional Encoding 값을 스칼라가 아닉 벡터 형태로 나타내 보도록 하겠습니다.
벡터 형태 중 가장 쉽게 사용할 수 있는 것이 2진수 형태로 나타내는 방법이 있습니다.

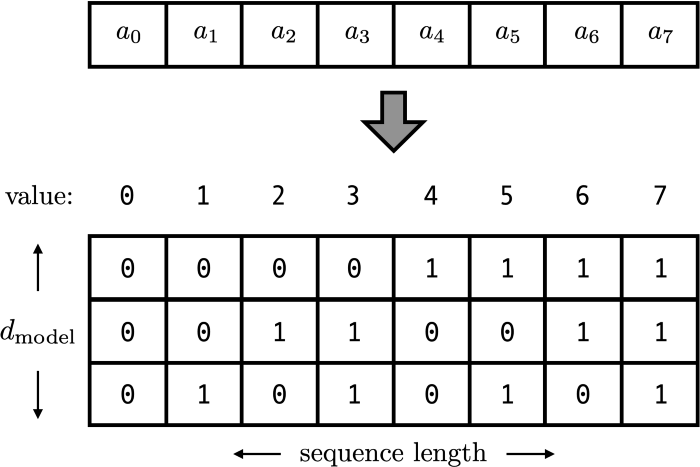
위 그림처럼 사용하면 \(2^{d}\) (\(d\) 는 벡터의 길이) 보다 작은 모든 길이에 대하여 동일한 Positional Encoding 값을 가질 수 있고 가변적인 길이에도 같은 위치라도 동일한 값을 가질 수 있습니다.
값의 범위 또한 크지 않고 0과 1 사이라서 학습에도 안정적으로 보입니다.

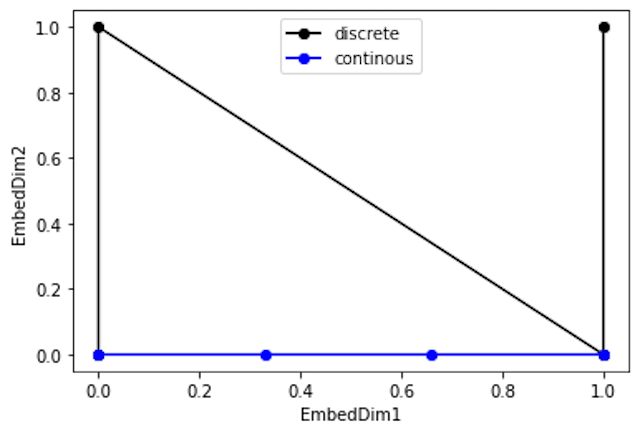
파란선과 검은선의 차이는 파란선은 점들 사이의 간격이 일정하지만 검은 점들 간 간격은 일정하지 않습니다.
앞의 ④ 위치 차이에 의한 Positional Encoding값의 차이를 거리로 이용 조건에 의해 검은색과 같은 Positional Encoding 값은 위배됩니다. 고차원을 증가할수록 이 차이는 점점 더 커져서 Positional Encoding으로 사용하기 부적합해집니다.

따라서 먼저 앞의 ①, ②, ③ 조건을 만족시키는 부드러운 곡선 형태를 찾고 ④, ⑤ 조건 또한 만족하도록 구성해 보겠습니다.
이러한 조건을 만족하는 대표적인 함수가 삼각함수 입니다. 삼각함수는 -1 ~ 1 사이의 값을 부드럽게 움직이므로 (②, ③) 조건을 만족하여 진동, 주기성과 관계가 있으므로 ①의 조건을 만족하므로 앞의 ① ~ ③ 조건에 부합합니다.

\[A\sin{(Nx)} \tag{1}\]

위 sin 함수에서 \(A\) 는 진폭과 관련되어 있고 \(N\) 은 진동수와 관련되어 있습니다. -1 ~ 1 사이의 진폭을 그대로 사용할 것이므로 \(A\) 는 Positional Encoding과 무관하며 \(N\) 을 통하여 진동수를 조절할 수 있습니다. \(N\) 의 값이 커지면 진동수가 커집니다. (주기는 짧아집니다.)
하지만 sin 함수를 사용하였을 때, 데이터의 길이가 커지게 되면 반복이 발생하여 ⑤ Positional Encoding 값은 위치에 따라 서로 다른 값을 가져야 한다는 조건을 만족할 수 없습니다.
따라서 위치에 따른 고유값을 가지게 하기 위하여 현실적인 데이터의 최대 길이를 고려하여 \(N\) 의 크기를 줄여 진동수를 작게 (주기는 길어집니다.) 만들면 됩니다. 그러면 단조 증가/감소 형식으로 나타내어지면서 고유값을 가지게 할 수 있습니다.
이러한 목적으로 Transformer의 저자는 \(N\) 값을 1/10000 과 같이 작은 값을 사용하였습니다.

마지막으로 ④ 조건만 만족하도록 구성하면 적합한 Positional Encoding이 됩니다. ④에서는 Position의 거리에 따른 Positional Encoding (PE)의 거리를 구할 수 있어야 합니다.
즉, Position의 변경량을 선형 변환으로 나타낼 수 있다면 Position의 변화에 따른 Positional Encoding의 차이를 등간격으로 구할 수 있어서 거리 값으로 나타낼 수 있습니다. 선형 변환 행렬을 \(T\) 라고 하였을 때, 아래와 같이 나타내는 것이 목적입니다.

\[\text{PE}(x + \Delta x) = \text{PE}(x) \cdot \text{T}(\Delta x) \tag{2}\]

위 식에서 PE는 Positional Encoding Matrix를 의미하고 Matrix의 크기는 (데이터의 길이, n) 을 가집니다. \(n\) 은 Positional Encoding의 Dimension을 의미하며 \(n\) 차원을 가짐을 나타냅니다.

\[\text{PE} = \begin{bmatrix} v^{(0)} \\ v^{(1)} \\ \vdots \\ v^{(\text{seq len -1})}\end{bmatrix} \tag{3}\]
\[v^{(i)} = \begin{bmatrix} \sin{(\omega_{0}x_{i})}, \cdots , \sin{(\omega_{n-1}x_{i})} \end{bmatrix} \tag{4}\]

식 (4)에서 정의된 \(v^{(i)}\) 을 식 (3)에 대입 시 PE의 크기를 확인할 수 있습니다.

\[\text{PE}(x + \Delta x) = \text{PE}(x) \cdot \text{T}(\Delta x) \tag{5}\]

식 (5)에서는 \(\text{T}(\Delta x)\) 에 해당하는 선형변환식에 의하여 Positional Encoding에서 차이가 발생하는 만큼을 계산할 수 있습니다.
삼각 함수를 사용할 때, \(x\) 가 각도라면 \(\Delta x\) 는 추가적으로 반영된 각도를 의미하는데 각의 회전 변환은 다음과 같은 식을 통하여 계산할 수 있습니다.

\[\begin{bmatrix} \cos{(\theta + \phi)} \\ \sin{(\theta + \phi)} \end{bmatrix} = \begin{bmatrix} \cos{(\phi)} & -\sin{(\phi)}\\ \sin{(\phi)} & \cos{(\phi)} \end{bmatrix} \begin{bmatrix} \cos{(\theta)} \\ \sin{(\theta)} \end{bmatrix} \tag{6}\]

식 (6)과 같은 translation 연산을 반영하기 위하여 sin 함수만을 사용하는 것 대신에 sin과 cos을 한 쌍으로 사용하는 것으로 \(v^{(i)}\) 를 변경합니다. 따라서 다음과 같이 \(v^{(i)}\) 를 구성합니다.

\[v^{(i)} = \begin{bmatrix} \sin{\omega_{0}x_{i}} & \cos{\omega_{0}x_{i}} & \cdots & \sin{\omega_{n-1}x_{i}} & \cos{\omega_{n-1}x_{i}} \end{bmatrix} \tag{7}\]

식 (7)과 같이 \(v^{(i)}\) 를 구성하면 \(2n\) 의 길이 만큼 값을 가지게 되고 행렬 Positional Encoding Matrix는 (데이터의 길이, 2n) 의 크기를 가지게 됩니다. 따라서 \(\Delta x\) 만큼 변화량을 block-diagonal 형태의 행렬 \(T(\Delta x)\) 를 이용하여 선형 변환을 통해 나타내면 다음과 같습니다.
block-diagonal은 대각 성분만 존재하고 나머지는 모두 0이되 대각 성분이 스칼라 값이 아니라 대각 성분 자체가 행렬이 되는 형태를 말합니다.

\[\text{PE}(x + \Delta x) = \text{PE}(x) \cdot \text{T}(\Delta x)\]
\[= \begin{bmatrix} \sin{\omega_{0}x_{0}} & \cos{\omega_{0}x_{0}} & \cdots & \sin{\omega_{n-1}x_{0}} & \cos{\omega_{n-1}x_{0}} \\ \sin{\omega_{0}x_{1}} & \cos{\omega_{0}x_{1}} & \cdots & \sin{\omega_{n-1}x_{1}} & \cos{\omega_{n-1}x_{1}} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \sin{\omega_{0}x_{\text{(seq_len-1)}}} & \cos{\omega_{0}x_{\text{(seq_len-1)}}} & \cdots & \sin{\omega_{n-1}x_{\text{(seq_len-1)}}} & \cos{\omega_{n-1}x_{\text{(seq_len-1)}}} \end{bmatrix} \begin{bmatrix} \begin{bmatrix} \cos{(\omega_{0}\Delta x)} & -\sin{(\omega_{0}\Delta x)}\\ \sin{(\omega_{0}\Delta x)} & \cos{(\omega_{0}\Delta x)} \end{bmatrix} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \begin{bmatrix} \cos{(\omega_{n-1}\Delta x)} & -\sin{(\omega_{n-1}\Delta x)}\\ \sin{(\omega_{n-1}\Delta x)} & \cos{(\omega_{n-1}\Delta x)} \end{bmatrix} \end{bmatrix} \tag{8}\]

식 (8)과 같이 회전 변환에 대한 행렬 연산이 전체 Positional Encoding Matrix에 적용되므로 \(\Delta x\) 만큼의 차이를 선형적으로 나타낼 수 있음을 확인하였습니다.

따라서 앞서 제시한 조건 ① ~ ⑤ 를 모두 만족하므로 다음과 같이 Positional Encoding Matrix 구성을 하는 것은 적합합니다.

Positional Encoding의 기본 형태

아래 식 (9), (10)은 Transformer 에서 사용한 Positional Encoding Matrix를 구성하는 방법입니다. pos는 데이터의 위치를 의미하고 \(i\) 는 Position을 표현하기 위한 차원의 인덱스를 나타냅니다. 즉, 짝수번째 차원은 sin을 사용하고 홀수번째 차원은 cos을 사용합니다. \(d_{\text{model}}\) 은 차원의 수를 나타냅니다. 10000은 Transformer에서 사용된 값이며 전제 조건 ①을 만족하는 범위에서 다른 값으로 변경 가능합니다.

\[\text{PE}_{(\text{pos}, 2i)} = \sin{(\frac{\text{pos}}{10000^{2i / d_{\text{model}}}})} \tag{9}\]
\[\text{PE}_{(\text{pos}, 2i + 1)} = \cos{(\frac{\text{pos}}{10000^{2i / d_{\text{model}}}})} \tag{10}\]
\[0 \le i \le d_{\text{model}} / 2\]

연속적인 데이터 하나 (ex. 문장)에 대하여 2차원 행렬이 하나 생기게 되고 그 행렬의 (y, x) 인덱스가 \((\text{pos}, 2i)\) , \((\text{pos}, 2i+1)\) 와 같이 표시됩니다.
따라서 연속적인 데이터의 갯수가 \(n\) (ex. 문장의 단어가 n개)이고 Position을 표현하기 위한 차원이 \(d_{\text{model}}\) 인 경우, 이 데이터에 대한 Positional Encoding Matrix는 식 (11)과 같이 정의됩니다.

\[\text{PE} = \begin{bmatrix} \text{PE}_{(0, 0)} & \text{PE}_{(0, 1)} & \cdots \text{PE}_{(0, d_{\text{model}} - 1)} \\ \vdots & \ddots & \vdots \\ \text{PE}_{(n-1, 0)} & \text{PE}_{(n-1, 1)} & \cdots \text{PE}_{(n-1, d_{\text{model}} - 1)} \end{bmatrix} \tag{11}\]

예를 들어 I am a Robot이란 데이터에 대하여 Poisitional Encoding Matrix를 만든다면 다음과 같습니다.

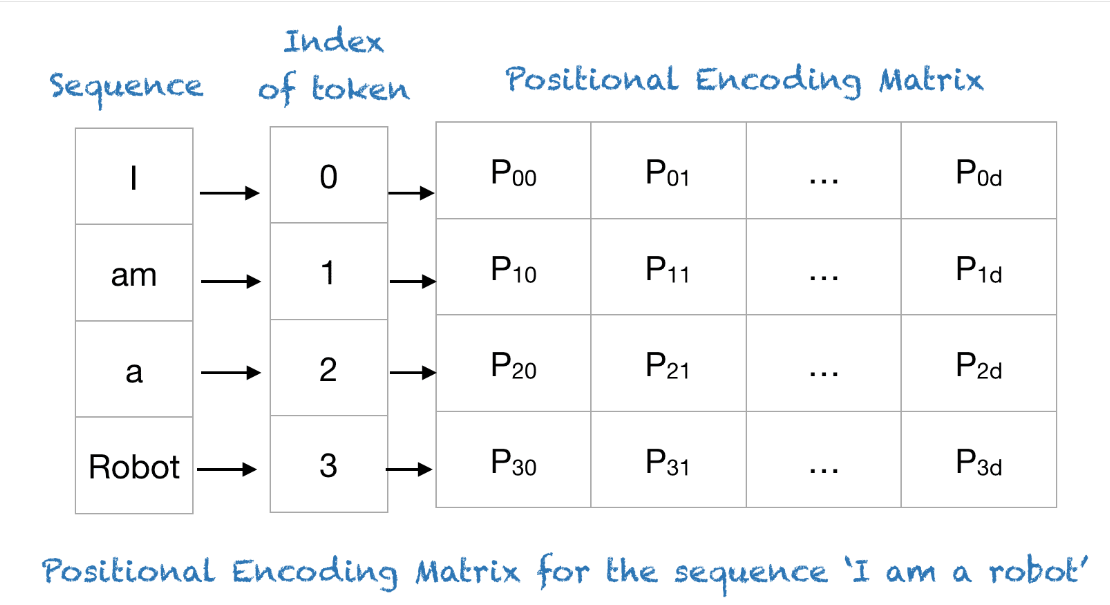
위 그림에서는 계산 편의상 Position을 나타내기 위한 차원은 4가 사용되었고 기존에 사용되었던 10000은 100으로 줄여서 행렬을 나타내었습니다.

행렬의 행은 데이터의 길이에 대응되면 행렬의 열은 Position을 나타내기 위한 차원에 해당하는데 이 차원은 어떻게 결정될까요?
앞에서 Positional Encoding Matrix은 입력 데이터와 덧셈 연산으로 합해진다고 하였습니다. 따라서 입력 데이터의 차원에 따라서 \(d_{\text{model}}\) 이 결정됩니다.
시퀀스 입력 데이터는 특성 연산을 통해 embedding vector로 변환됩니다. 위 예시에서 I, am, a, Robot 각각은 (4, ) 크기의 벡터로 표현하여 연산할 수 있도록 만듭니다. 이 벡터를 embedding vector라고 합니다.
따라서 I am a Robot은 (4, 4) 크기의 행렬이 되며 이 크기에 맞춰서 Positional Encoding Matrix 또한 생성됩니다.

이 행렬과 차원이 맞는 positional encoding matrix를 생성하여 덧셈 연산을 도식화 하면 아래 그림과 같습니다.

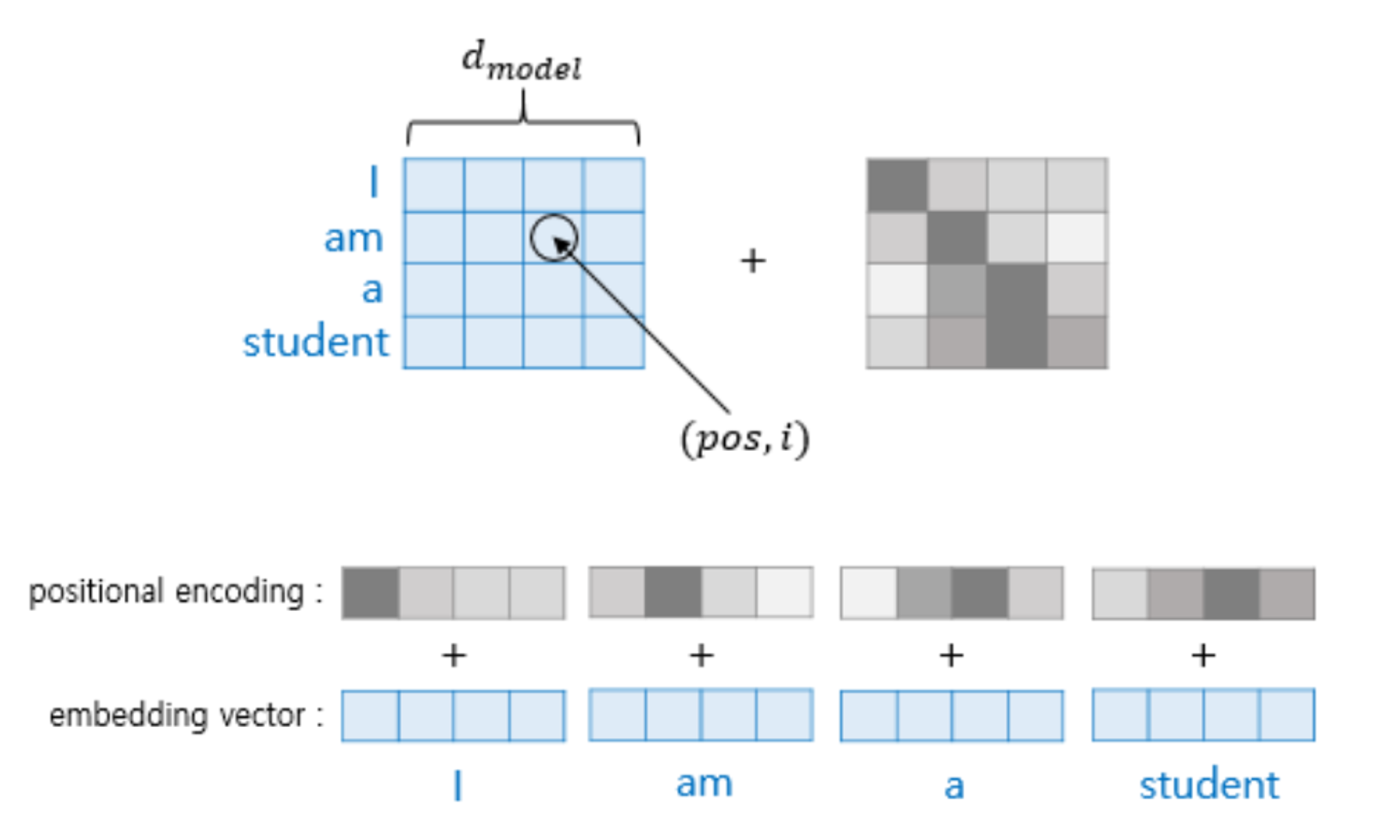
Positional Encoding Matrix를 시각화하여 나타내면 다음과 같습니다.

import numpy as np
import matplotlib.pyplot as plt
 
def getPositionEncoding(seq_len, d, n=10000):
    P = np.zeros((seq_len, d))
    for k in range(seq_len):
        for i in np.arange(int(d/2)):
            denominator = np.power(n, 2*i/d)
            P[k, 2*i] = np.sin(k/denominator)
            P[k, 2*i+1] = np.cos(k/denominator)
    return P
 
P = getPositionEncoding(seq_len=4, d=4, n=100)
print(P)

# [[ 0.          1.          0.          1.        ]
#  [ 0.84147098  0.54030231  0.09983342  0.99500417]
#  [ 0.90929743 -0.41614684  0.19866933  0.98006658]
#  [ 0.14112001 -0.9899925   0.29552021  0.95533649]]

P = getPositionEncoding(seq_len=100, d=512, n=10000)
cax = plt.matshow(P)
plt.gcf().colorbar(cax)

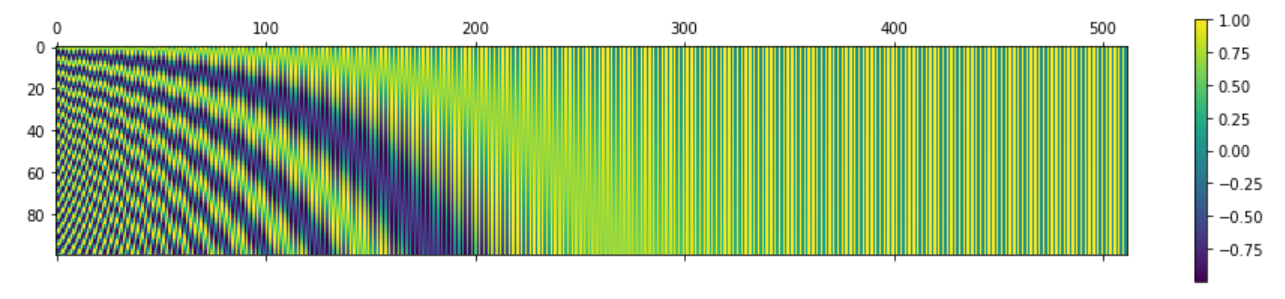
위 그림을 살펴보면 각 행들이 서로 다른 값의 형태를 가짐을 확인할 수 있고 연속적으로 증감하는 형태를 보여 Positional Encoding Matrix의 전제 조건을 만족해 보입니다.

Positional Encoding의 위치 유사성 계산

Transformer 모델에서는 대부분의 연산이 내적 (inner product)에 의하여 연산됩니다. Positional Encoding Matrix가 Embedding 행렬에 더해져서 연산이 되나 그 사용 목적은 각 데이터의 위치 정보를 보존하기 위함입니다.
따라서 Positional Encoding Matrix 내부에서 가까운 행 끼리는 유사도가 높고 멀리 있는 행 끼리는 유사도가 낮아야 위치 정보가 유지됨을 확인할 수 있습니다.

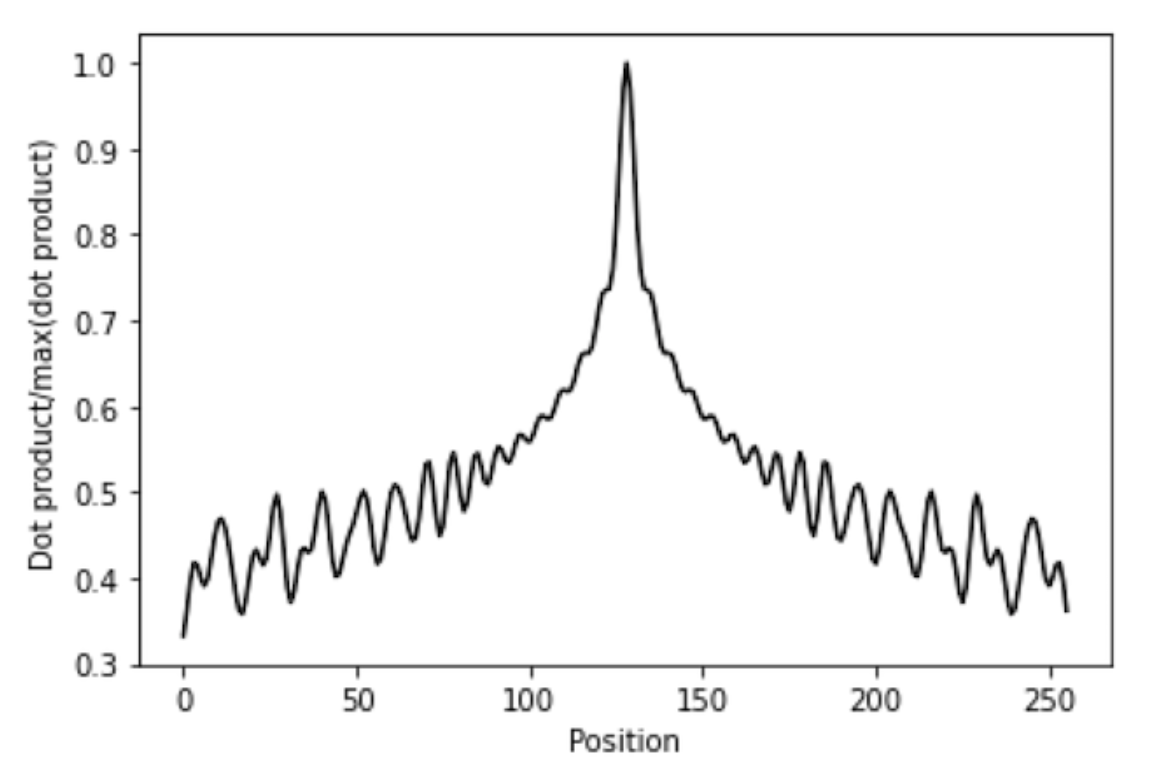
위 그래프는 (256, 128) 크기의 Positional Encoding Matrix에서 128번째 행을 기준으로 나머지 1 ~ 256 번째 행과의 내적을 통해 유사도를 나타낸 것입니다. 1에 가까울수록 유사도가 높고 0에 가까울수록 유사도가 낮습니다.
위 그래프와 같이 128번째 행에서 멀어질수록 유사도가 낮아지는 경향을 살펴볼 수 있습니다.

Positional Encoding의 Pytorch 코드

아래 코드는 Pytorch를 이용하여 Positional Encoding Matrix를 구하는 방법 입니다.

import torch
import matplotlib.pyplot as plt
import numpy as np
from torch import nn

class PositionalEncoding(nn.Module):
    
    def __init__(self, seq_len, d_model, n, device):
        
        super(PositionalEncoding, self).__init__() # nn.Module 초기화
        
        # encoding : (seq_len, d_model)
        self.encoding = torch.zeros(seq_len, d_model, device=device)
        self.encoding.requires_grad = False
        
        # (seq_len, )
        pos = torch.arange(0, seq_len, device=device)
        # (seq_len, 1)         
        pos = pos.float().unsqueeze(dim=1) # int64 -> float32 (없어도 되긴 함)
        
        _2i = torch.arange(0, d_model, step=2, device=device).float()
        
        self.encoding[:, ::2] = torch.sin(pos / (n ** (_2i / d_model)))
        self.encoding[:, 1::2] = torch.cos(pos / (n ** (_2i / d_model)))
        
        
    def forward(self, x):
        # x.shape : (batch, seq_len) or (batch, seq_len, d_model)
        seq_len = x.size()[1] 
        # return : (seq_len, d_model)
        # return matrix will be added to x by broadcasting
        return self.encoding[:seq_len, :]

seq_len = 100
d_model = 512
sample_pos_encoding = PositionalEncoding(seq_len=seq_len, d_model=d_model, n=10000, device='cuda')
positional_encoding_matrix = sample_pos_encoding.encoding.detach().cpu().numpy()
cax = plt.matshow(P)
plt.gcf().colorbar(cax)

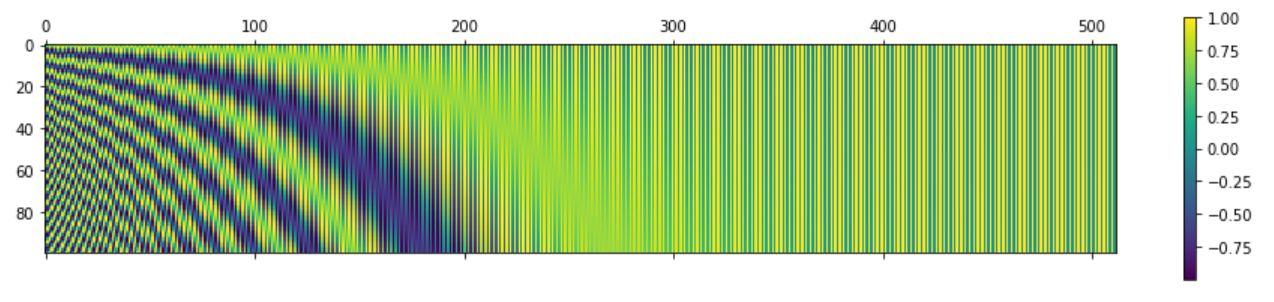
앞에서 numpy를 통해 구한 결과와 동일한 것을 확인할 수 있습니다.

x = torch.rand(10, seq_len, d_model).cuda()
print(x.shape)
# torch.Size([10, 100, 512])

x_added_PE = x + sample_pos_encoding(x)
print(x_added_PE.shape)
# torch.Size([10, 100, 512])

Embedding Matrix와 덧셈 연산을 할 때에는 broadcasting을 통하여 batch 단위로 연산이 될 수 있도록 적용하였습니다.

Nerf에서의 Positional Encoding의 필요성

최근 화두로 떠오르는 NERF(Neural Radiance Field) 논문에서 또한 Positional Encoding이 사용됩니다. 사용 방식은 Transformer에서 사용한 방식과 같으나 사용 목적이 다릅니다.
본 글에서 살펴본 바와 같이 Transformer에서는 연속적으로 입력되는 데이터를 병렬처리 할 때, 순서를 기억하기 위하 Positional Encoding을 사용하며 입력 데이터의 갯수나 크기에 영향 없이 사용하기 위하여 sin, cos 형태를 사용하였습니다.
반면 NERF에서는 sin과 cos을 이용하여 Fourier Feature를 추가하기 위한 용도로 사용합니다. Frequency 도메인에서의 Feature를 low frequency 부터 high frequency 까지 추가하면 이미지 생성 시 그 특성을 반영하여 고화질의 이미지가 정교하게 생성됩니다.

딥러닝 Concept 관련 글 목차