딥러닝의 Quantization (양자화)와 Quantization Aware Training

deep learning 관련 글 목차

참조 : https://arxiv.org/pdf/2103.13630.pdf (A Survey of Quantization Methods for Efficient Neural Network Inference)
참조 : https://arxiv.org/pdf/1806.08342.pdf (Quantizing deep convolutional networks for efficient inference: A whitepaper)
참조 : https://arxiv.org/pdf/2004.09602.pdf (INTEGER QUANTIZATION FOR DEEP LEARNING INFERENCE: PRINCIPLES AND EMPIRICAL EVALUATION)
참조 : https://youtu.be/Oh1pLlir39Q
참조 : https://leimao.github.io/article/Neural-Networks-Quantization/
참조 : https://leimao.github.io/blog/PyTorch-Quantization-Aware-Training/
참조 : https://spell.ml/blog/pytorch-quantization-X8e7wBAAACIAHPhT
참조 : https://www.youtube.com/playlist?list=PLC89UNusI0eSBZhwHlGauwNqVQWTquWqp
참조 : https://wannabeaprogrammer.tistory.com/42
참조 : https://youtu.be/DDelqfkYCuo
참조 : https://www.tensorflow.org/model_optimization/guide/quantization/training_example

Quantization 이란

Quantization은 실수형 변수(floating-point type)를 정수형 변수(integer or fixed point)로 변환하는 과정을 뜻합니다.

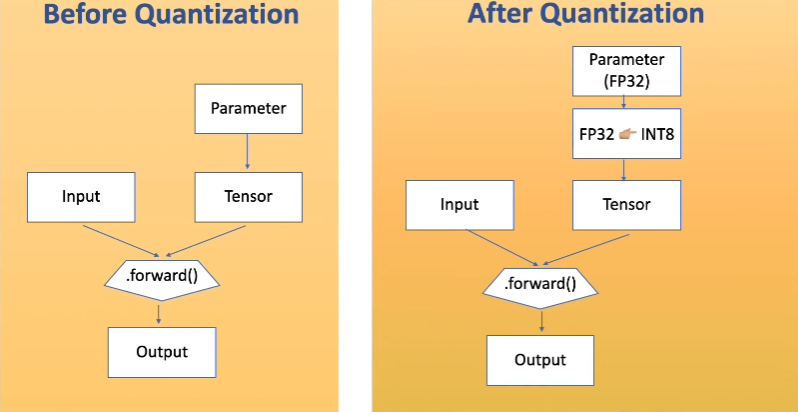
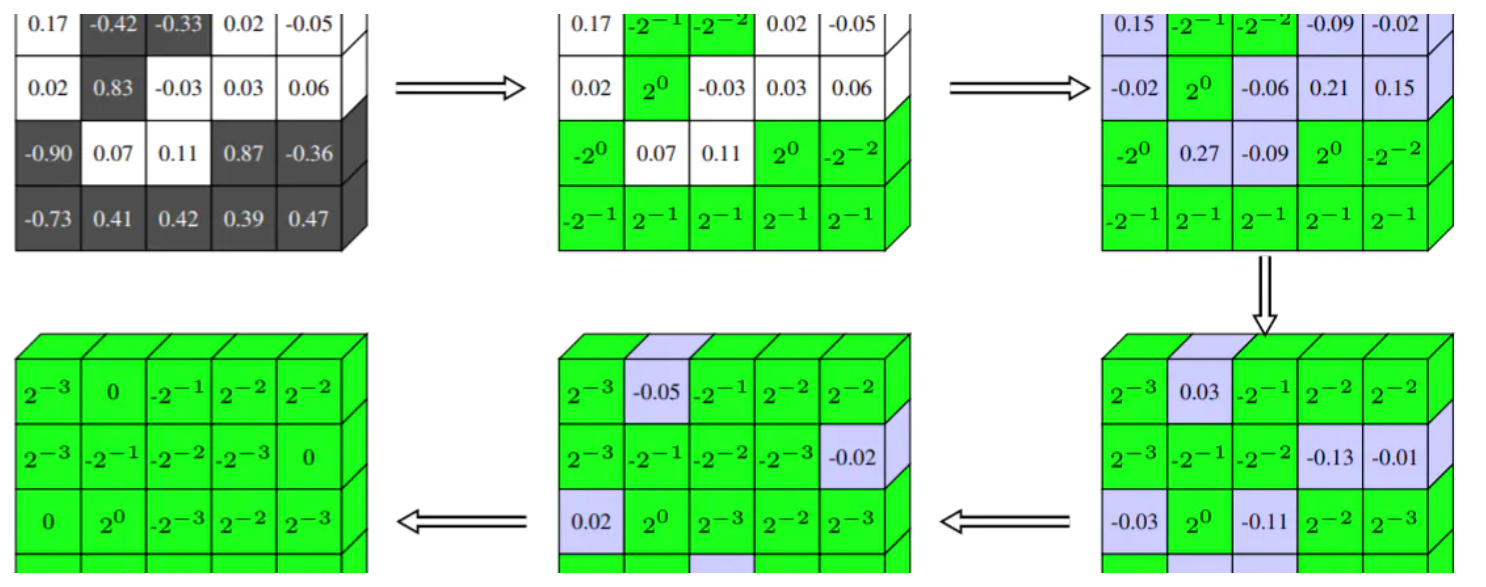
예를 들어 위 그림과 같이 Quantization을 적용하면 일반적으로 많이 사용하는 FP32 타입의 파라미터를 INT8 형태로 변환한 다음에 실제 inference를 하게됩니다.

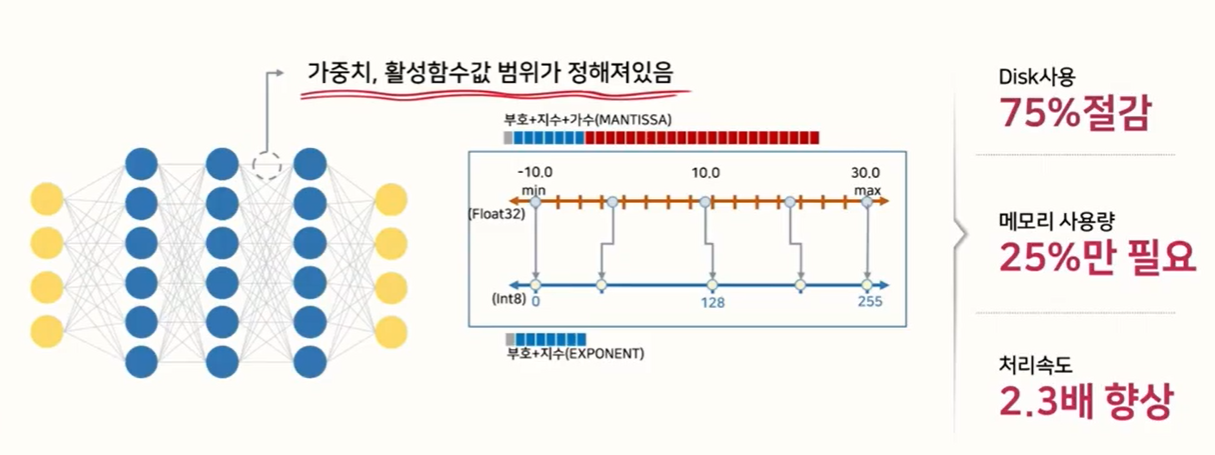
이 작업은 weight나 activation function의 값이 어느 정도의 범위 안에 있다는 것을 가정하여 이루어 지는 모델 경량화 방법입니다.
위 그림과 같이 floating point로 학습한 모델의 weight 값이 -10 ~ 30 의 범위에 있다고 가정하겠습니다. 이 때, 최소값인 -10을 uint8의 0에 대응시키고 30을 uint8의 최대값인 255에 대응시켜서 사용한다면 32bit 자료형이 8bit 자료형으로 줄어들기 때문에 전체 메모리 사용량 및 수행 속도가 감소하는 효과를 얻을 수 있습니다.

이와 같이 Quantization을 통하여 효과적인 모델 최적화를 할 수 있는데, float 타입을 int형으로 줄이면서 용량을 줄일 수 있고 bit 수를 줄임으로써 계산 복잡도도 줄일 수 있기 때문입니다. (일반적으로 정수형 변수의 bit 수를 N배 줄이면 곱셈 복잡도는 N*N배로 줄어듭니다.)
또한 정수형이 하드웨어에 좀 더 친화적인 이유도 있기 때문에 Quantization을 통한 최적화가 필요합니다.
정리하면 ① 모델의 사이즈 축소, ② 모델의 연산량 감소, ③ 효율적인 하드웨어 사용이 Quantization의 주요 목적이라고 말할 수 있습니다.

간단하게 floating point 대신 int형을 사용해야 하는 지 살펴보면 다음과 같습니다.

import time
t1 = time.time()
print(3.123456789 - 2.345678912)
t2 = time.time()
print(3 - 2)
t3 = time.time()

print((t2 - t1))
# 0.025929689407348633
print((t3 - t2))
# 0.023936748504638672
print((t2 - t1) / (t3 - t2))
# 1.083258630650013

위 코드 결과와 같이 단순히 1개의 연산만을 할 경우에도 소수 연산이 정수 연산보다 8% 만큼의 시간이 더 걸리는 것을 확인할 수 있습니다.

딥러닝에서의 Quantization의 역할에 대해서 다음과 같이 살펴보도록 하곘습니다.

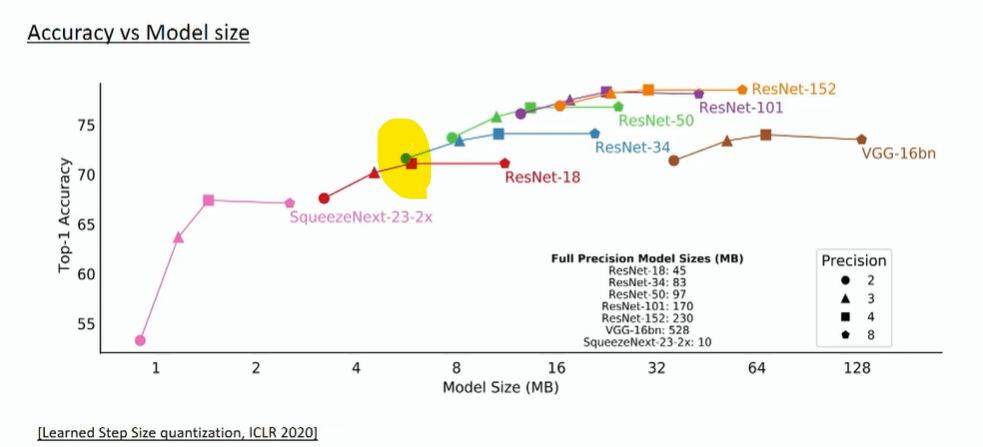
예를 들어 위 그림의 형광펜을 칠한 위치를 살펴보겠습니다. Precision에 해당하는 2, 3, 4, 8은 Quantization 하였을 때, 사용한 bit가 됩니다. ResNet-34를 2 bit로 표현하였을 때의 Top-1 Accuracy가 ResNet-18을 4-bit로 표현하였을 때 보다 성능이 더 좋은 것을 알 수 있습니다. 이 때 모델 사이즈는 오히려 ResNet-34가 조금 더 가벼운 것도 확인할 수 있습니다.
즉, 여기서 얻을 수 있는 교훈은 작은 네트워크로 quantization을 대충하는 것 보다 큰 네트워크로 quantization을 더 잘하는게 성능 및 모델 사이즈 측면에서 더 좋을 수 있다는 점입니다.
FP32 대신 INT8을 사용한다면 보통 model size는 1/4이 되고 inference speed가 2 ~ 4배 빨라지며 memory bandwidth도 2 ~ 4배 가벼워집니다.

Weight Quantization 요약

먼저 딥러닝 시 사용할 Quantization에 관한 용어 및 내용을 간략하게 정리해 보도록 하겠습니다. 좀 더 상세한 내용은 아래 Quantization Mapping 이란 부분부터 글 끝까지 설펴보시면 되고 간략하게 전체 내용을 훑고 싶으시면 Weight Quantization 요약 부분만 빠르게 읽으시면 됩니다.

내용을 살펴보기에 앞서서 딥러닝에서의 Quantization을 할 때 아래 5가지 전제조건을 숙지하도록 하겠습니다.

① Inference Only : Quantization은 inference에서만 사용합니다. 즉, 학습 시간을 줄이기 위한 것과는 관련이 없습니다.
② Not every layer can be quantized : 구현한 딥러닝 모델의 모든 layer가 quantization이 될 수 없는 경우가 있습니다. 이것은 각 layer 자체의 특수성으로 어려운 부분도 있지만 Pytorch와 같은 Framework가 지원하지 않는 경우도 있습니다.
③ Not every layer shoud be quantized : 모든 layer가 반드시 quantization이 되어야 하는 것이 가장 효율적인 것은 아닙니다. 경우에 따라서는 layer를 fusion 하여 한번에 quantization을 하기도 합니다.
④ Not every model reacts the same way to quantization : 같은 quantization을 적용하더라도 모든 딥러닝 모델이 동일한 효과가 나타나는 것은 아닙니다. 앞의 layer에서도 말했듯이 layer의 특성이 있기 때문에 layer의 집합인 model에서는 그 현상이 더 크게 나타납니다.
⑤ Most available implementations are CPU only : quantization이 적용된 많은 연산이 아직 CPU에서 사용해야 하는 경우도 있습니다.

딥러닝에서의 Quantization은 아래와 같이 6가지 단계를 가지게 됩니다.
① Module Fusion : layer들을 하나로 묶어주는 Fusion 단계를 의미합니다. 이 단계는 반드시 필요한 것은 아니지만 좋은 성능을 위해서 많이 사용하고 있습니다. 대표적으로 Conv-BatchNorm-ReLU를 Fusion 하는 방법을 많이 사용하고 있습니다. 이 작업은 필요시에만 사용합니다.
② Formula Definition : Qunaitization 시 사용하는 식을 정의합니다. 일반적으로 FP32 → INT8의 방식을 사용하며 반대로 다시 Floting Point로 변경 시 INT8 → FP32로 변경하는 Dequantization 방법도 정의합니다.
③ Hardware Deployment :하드웨어에 따라서 어떻게 calibration하는 지 달라집니다. 대표적으로 인텔계열과 ARM계열이 있습니다.
④ Dataset Calibration : weight를 변환하기 위한 식의 파라미터를 Dataset을 이용하여 계산합니다.
⑤ Weight Conversion : 실제 weight를 FP 타입에서 INT 타입으로 변환합니다.
⑥ Dequantization : 마지막으로 inference를 통해 얻은 출력을 dequantization을 통하여 다시 Floating 타입으로 변경합니다. 이 작업은 필요시에만 사용합니다.

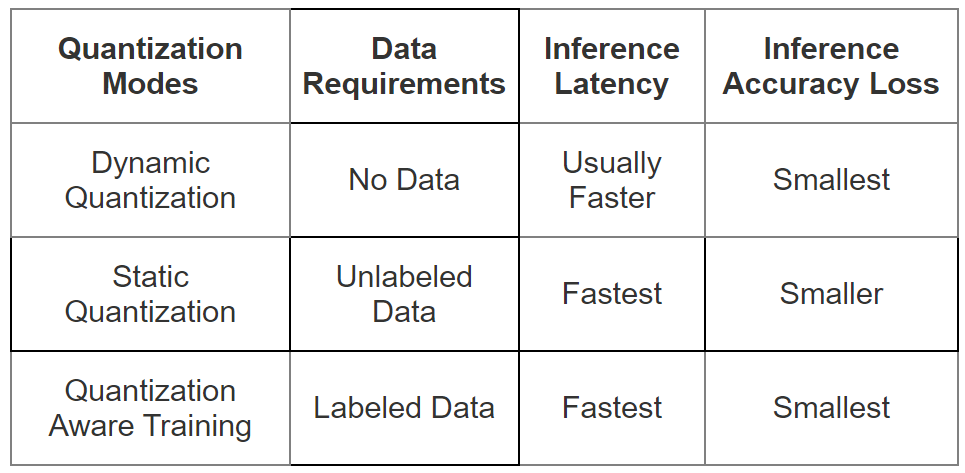
이 글에서 다룰 Quantization 테크닉은 크게 3가지 입니다. ① Dynamic Quantization, ② Static Quantization, ③ Quantization Aware Training 이며 위 6단계 설 명과 더불어서 설명하도록 하겠습니다.

① Module Fusion

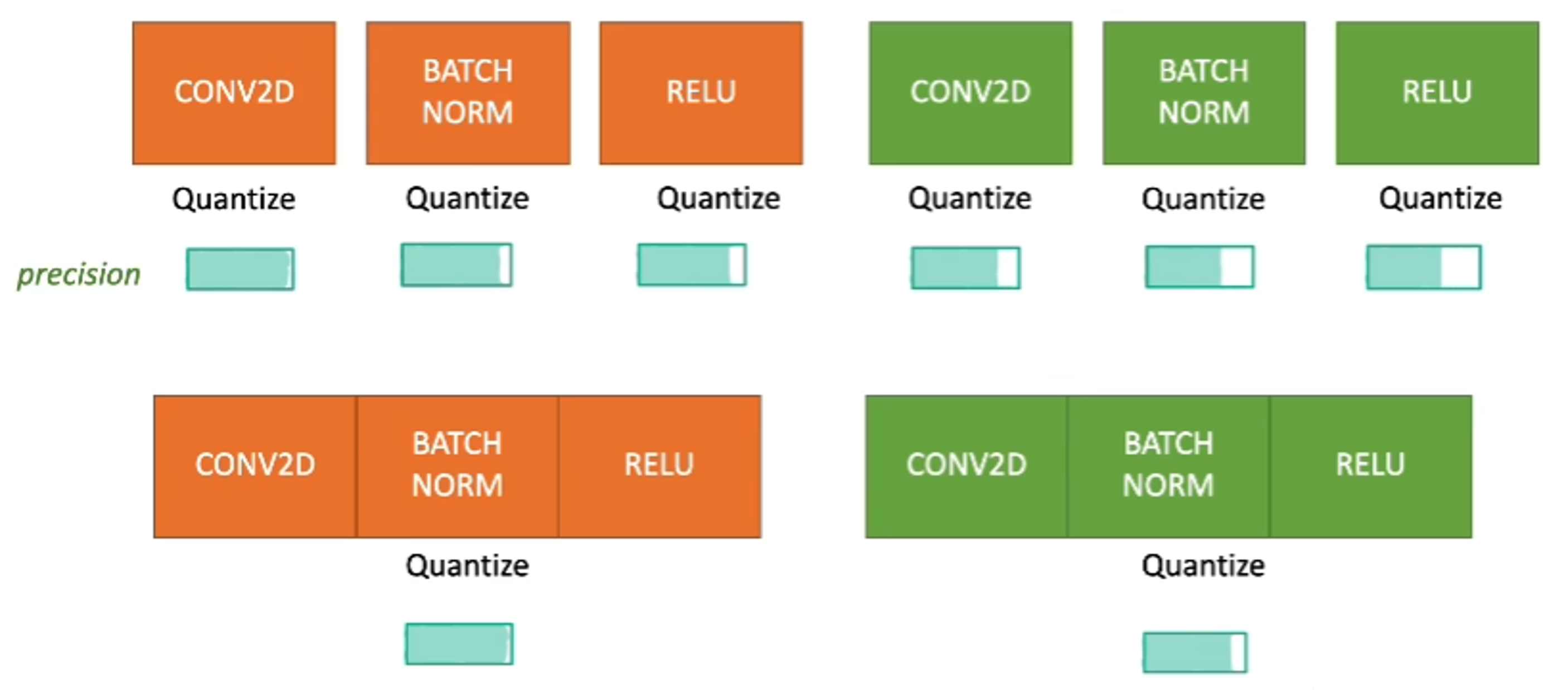
위 그림을 살펴보면 CONV2D - BATCHNORM - RELU가 한 쌍으로 되어 있습니다. 실제 이 순서대로 layer를 많이 쌓기 때문에 실제 사용 케이스와 유사합니다. 주황색은 첫번째 모듈이고 초록색은 두번째 모듈을 뜻합니다.
위 그림에서 첫번째 행에 소개된 내용은 CONV2D, BATCHNORM, RELU 각각을 quantization을 적용한다는 뜻이고 두번째 행에 소개된 내용은 CONV2D - BATCHNORM - RELU을 하나로 묶어서 한번만 quantization을 한다는 뜻입니다.
첫번째 행의 precision을 살펴보면 quantization이 적용된 layer를 걸칠때마다 precision이 감소하는 것을 알 수 있습니다.
따라서 같은 모듈에서 quantization 하는 횟수를 3번에서 1번으로 줄여서 정확도를 얻고자 하는 방법으로 Moudel Fusion이 사용됩니다. 이와 같이 모든 layer에 quantization을 적용하지 않는 이유는 크게 2가지가 있습니다.
quantization 횟수를 줄이면 inference time (less quantization eperations)과 precision (less approximation)을 개선할 수 있기 때문입니다. 하지만 과도하게 quantization 횟수를 줄여버리면 quantization 자체의 목적이 사라질 수 있기 때문에 어느 부분에 Module Fusion을 하는 것이 좋은지 또한 연구 분야입니다. 따라서 사용하는 입장에서는 이미 성능 효과가 나타난 CONV2D - BATCHNORM - RELU에 대한 Module Fusion을 하기를 권장합니다.

② Formula Definition

Quantization의 가장 큰 핵심인 어떻게 Quantization을 하는 지 formula를 정하는 방법에 대하여 살펴보도록 하겠습니다.

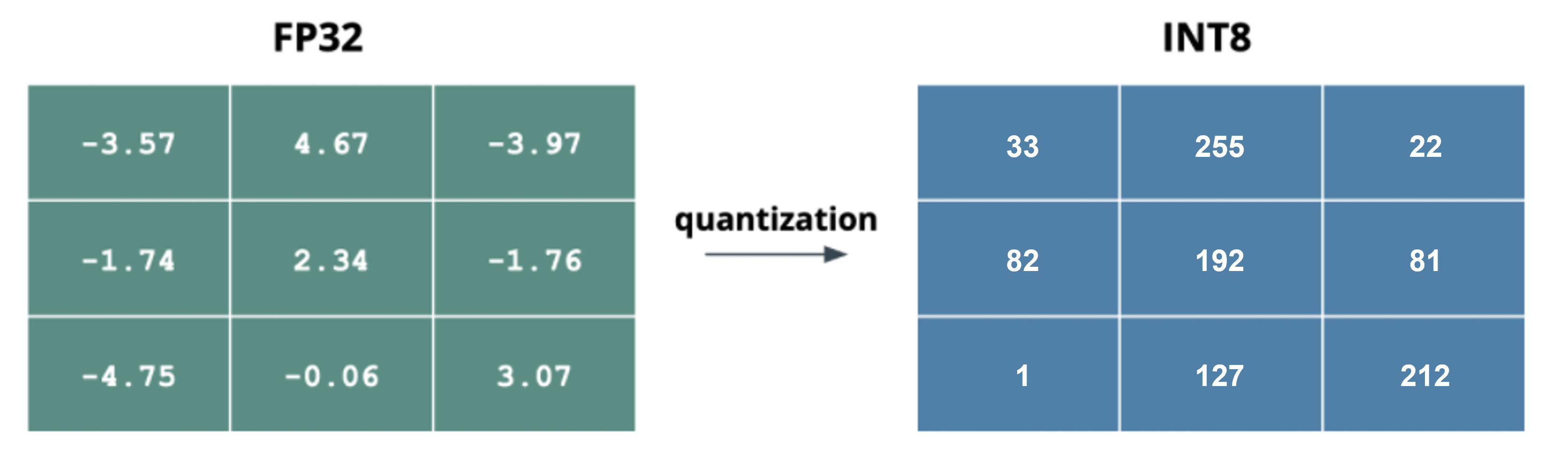
위 그림의 왼쪽이 FP32일 때의 숫자이고 오른쪽은 formula를 통해 변환한 INT8에 해당하는 값입니다. 실제로는 FP32과 INT8의 숫자는 딥러닝 모델의 weight에 해당한다고 보시면 됩니다. 위 도표를 통해서 아래 식 (1), (2), (4)을 통해 정의한 Formula를 연산해 보도록 하겠습니다. 식의 상세 내용은 Quantization Mapping 이란 부터 읽어보시면 됩니다.

\[f_{q}(x, s, z) = \text{Clip}(\text{round}(\frac{x}{s}) + z) \tag{1}\]
\[f_{q}(x, s, z) : \text{quantized value}\]
\[\text{clip}() : \text{clip the values in a range (ex. 0 ~ 255)}\]
\[x : \text{real value (float32)}\]
\[s : \text{scale}\]
\[z : \text{zero-point integer}\]

위 식에서 input은 $r$ 이고 이 값을 $Q$ 로 변환하기 위해서는 $s, z$ 의 값이 정해져야 합니다. 그러면 $s, z$ 값을 정의해 보도록 하겠습니다.

\[s = \frac{\beta - \alpha}{\beta_q - \alpha_q} \tag{2}\]
\[\alpha, \beta : \text{min/max values of filter/layer}\]
\[\alpha_q, \beta_q : \text{min/max values of quantized value}\]

이 부분의 식을 정의하기 위해서는 칩이 ARM인지 INTEL 계열인 지 먼저 알아야 합니다. ARM은 MinMax를 이용하여 $s$ 를 구하는 반면 INTEL 계열은 히스토그램 알고리즘을 이용합니다. 식 (2)는 ARM의 MinMax를 이용하는 예시입니다.
이 글의 예제는 식 (2)를 이용하여 $s$ 를 구하며 filter 또는 layer의 최소값은 $\alpha$, 최댓값은 $\beta$ 를 이용하여 식 (1)의 clip 함수를 구현하기도 합니다. (다른 방법들도 있습니다.) 이 때, clip의 range는 $[\alpha, \beta]$ 가 됩니다.
위 식에서 $\alpha_q, \beta_q$ 는 quantization을 하였을 때, 최솟값과 최댓값이 되며 정수를 가집니다. 보통 INT8로 quantization을 할때, unsigned 형태를 사용하면 0 ~ 255 까지의 값을 가지고 signed 형태를 사용하면 -128 ~ 127의 값을 가지게 됩니다.

위 표에서 최댓값은 4.67이고 최솟값은 -4.75입니다. 따라서 $\alpha = -4.75$, $\beta = 4.67$ 가 됩니다. 그리고 FP32 → INT8 (UNSIGNED)로 변경한다고 가정하면 $\alpha_q = 0, \beta_q = 255$ 가 됩니다.

\[s = \frac{\beta - \alpha}{\beta_q - \alpha_q} = \frac{4.67 - (-4.75)}{255 - 0} = \frac{9.42}{255} = 0.037 \tag{3}\]

마지막으로 $z$ 식을 정의해 보도록 하겠습니다.

\[z = \text{round}\big(\frac{\beta \alpha_q - \alpha \beta_q}{\beta - \alpha}\big) \tag{4}\]

위 식을 이용하여 $z$ 를 구하면 다음과 같습니다.

\[z = \text{round}\big(\frac{4.67*0 - (-4.75)*255}{4.67 - (-4.75)} \big) = 129 \tag{5}\]

지금까지 $s, z$ 를 구하였으므로 $x = -3.57$ 이라고 가정하고 식 (1)을 이용하여 quantization을 진행해 보도록 하겠습니다. 이 때, clip은 잠시 생략하겠습니다.

\[q = \text{round}(\frac{x}{s}) + z = \text{round}(\frac{-3.57}{0.037}) + 129 = 33 \tag{6}\]

마지막으로 clipping 개념만 적용하면서 마무리 하겠습니다. clipping 방법은 다양한 방법이 있지만 여기서 다룰 clipping 방법은 간단하게 lower_bound와 upper_bound를 이용하여 값을 $\alpha_q, \beta_q$ 범위안의 값을 가지도록 하는 것입니다.

\[\begin{align} \text{clip}(x, \alpha_q, \beta_q) &= \begin{cases} \alpha_q & \text{if $x < \alpha_q $} \\ x & \text{if $\alpha_q \leq x \leq \beta_q$}\\ \beta_q & \text{if $x > \beta_q$}\\ \end{cases} \end{align} \tag{7}\]

식 (7) 까지 적용하면 식 (1) 전체를 이해하실 수 있습니다. 식의 자세한 전개는 글 뒷부분에서 확인하시면 도움이 됩니다.

위 과정 전체를 실습해 보려면 아래 colab 링크를 참조하시기 바랍니다.
링크 : How to Quantize

③ Hardware Deployment

앞에서 설명한 바와 같이 하드웨어에 따라서 어떻게 calibration하는 지 달라집니다. 대표적으로 인텔계열과 ARM계열이 있고 인텔 칩을 사용하는 경우 히스토그램 방식을 이용하고 ARM 칩을 사용하는 경우 위 글에서 다룬 MinMax 방식을 이용합니다.

④ Dataset Calibration

MinMax 방법 또는 히스토그램 방법이든 식 (2)의 스케일 값인 $S$ 를 정할 때 $\alpha, \beta$ 와 같은 범위값을 정하여 formula에 필요한 파라미터를 모두 정의합니다.

⑤ Weight Conversion

④ 과정을 통하여 formula가 정의되면 FP32에 대하여 INT8로 변환합니다.

마지막인 ⑥ Dequantization은 INT8의 결과를 다시 FP32로 변환하는 것이며 상세 식은 Quantization Mapping에서 다루겠습니다. 다만 기억하실 점은 FP32 → INT8로 변환 시 정보 손실이 발생하기때문에 역으로 INT8 → FP32로 변환 시 잃어버린 정보로 인하여 그대로 변환되지 않습니다. 이 때 발생하는 Error를 Quantization Error라고 하며 이 Error를 줄이는 것이 좋은 Quantization 알고리즘이라고 말할 수 있습니다.

Symmetric vs Asymmetric Quantization

range를 결정하는 $\alpha, \beta$ 가 절대값이 같은 값으나 부호가 다르게 사용된다면 Symmetric이라고 하고 서로 다른 절대값을 가지는 경우라면 Asymmetric 이라고 합니다.

앞에서 다룬 위 예시에서 최솟값은 -4.75이고 최댓값은 4.67입니다. 최솟값과 최댓값이 다르므로 이 값을 그대로 사용한다면 Asymmetric 하게 됩니다. Symmetric 하게 하려면 최솟값과 최댓값 중 절대값이 큰 값을 선택한 다음에 $\alpha, \beta$ 로 사용하면 됩니다. 다음과 같습니다.

Symmetric quantization : $[-4.75, 4.75]$
Asymmetric quantization : $[-4.75, 4.67]$

즉, Symmetric quantization을 사용할 때에는 $\alpha = -\beta$ 가 되기 때문에 식 (4)에 대입하면 다음과 같이 식이 간단해 집니다.

\[z = \text{round}\big(\frac{\beta \alpha_q - \alpha \beta_q}{\beta - \alpha}\big) = \text{round}\big(\frac{\beta \alpha_q - (-\beta) \beta_q}{\beta - (-\beta)}\big) = \text{round}\big(\frac{\beta(\alpha_q + \beta_q)}{2\beta}\big) = \text{round}\big(\frac{\alpha_q + \beta_q}{2}\big) \tag{8}\]

만약 식 (8) 에서 INT8의 범위가 -128 ~ 127 이라고 가정하면 식 (8)을 통해 $z = 0$ 임을 알 수 있습니다.
여기 까지 진행된 내용을 통하여 FP32 → INT8로 mapping을 한 다음에 outlier가 발생 시 INT8의 최솟값 또는 최댓값으로 clipping 되도록 적용하면 quantization이 마무리 됩니다.

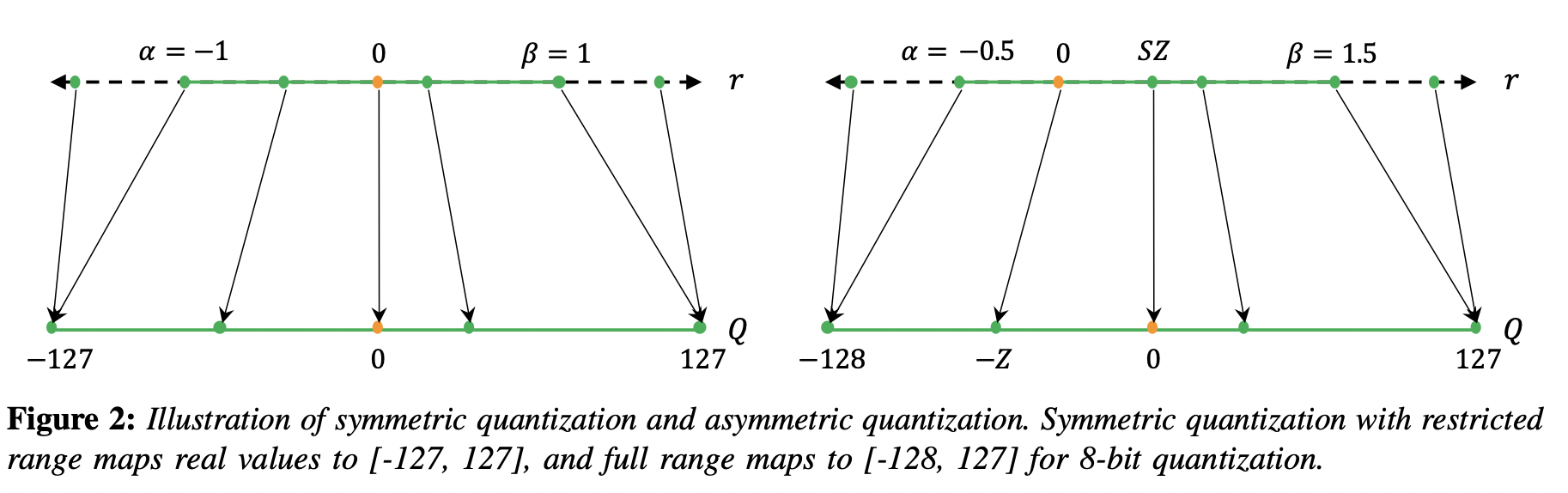
위 그림의 왼쪽은 Symmetric quantization이고 오른쪽은 Asymmetric quantization 입니다. Floating point에서의 시작점이 왼쪽 그림에서는 $[-1, 1]$ 사이인 반면에 오른쪽 그림은 $[-0.5, 1.5]$ 인 것을 알 수 있습니다.

Static vs Dynamic Quantization

Static과 Dynamic의 의미는 앞에서 설명한 clipping range를 어떻게 정하는 지에 따라 달라집니다.
static quantization : clipping range는 사전에 미리 계산이 되어서 inference 시에는 고정된 값으로 사용되는 방법을 의미합니다. 고정된 clipping range를 사용하기 때문에 이 방법은 추가적인 계산 비용이 발생하지 않지만 dynamic quantization 방법에 비해 낮은 성능을 보이곤 합니다. static quantization의 clipping range를 사전에 정하는 대표적인 방법은 샘플 입력 데이터를 준비하여 range를 정해보는 것입니다. 이 방법을 calibration이라고 부릅니다.
dynamic quantization : 동작 중 (runtime)에 각 activation map에 해당하는 clipping에서 clipping range가 동적으로 계산됩니다. 동작 중에 동적으로 계산되어야 하기 때문에 실시간성이 보장되는 계산 방법이 이용되며 대표적으로 min, max, percentile 등이 있습니다. 추가 계산 비용이 들지만 매번 input에 맞춰서 clipping range가 결정되기 때문에 dynamic quantization 방법은 static quantization 방법보다 더 좋은 성능을 가집니다.

Quantization Mapping 이란

지금부터 앞에서 다룬 내용을 좀 더 자세하게 다루어 보도록 하겠습니다.
먼저 Quantization의 의미를 수식으로 알아보도록 하겠습니다. floating point 값인 $x \in [\alpha, \beta]$ 를 quantized가 적용된 값인 $x_q \in [\alpha_q, \beta_q]$ 라고 한다면 de-quantization의 과정은 다음과 같습니다.

\[x = c (x_q + d)\]

즉, floating point 값인 $x$ 는 quantized된 정수값 $x_{q}$ 를 통해 $x = c (x_q + d)$ 로 나타나짐을 알 수 있습니다.
반대로 quantization의 과정은 다음과 같이 나타낼 수 있습니다.

\[x_q = \text{round}\big(\frac{1}{c} x - d\big)\]

위 식에서 $c, d$ 는 Quantization 시 필요한 변수입니다. 위 식에서 $x_{q}$ 는 integer형태이지만 floating point $x$ 를 $c$ 로 나누게 되면서 생기게 되는 오차가 발생합니다. (round 처리를 하면서 버림/올림을 하게 되면 발생하게 되는 오차입니다.) 이 때, 발생하는 오차가 주요한 quantization error가 된다고 말할 수 있습니다.

구해야 하는 변수가 $c, d$ 2개이므로 2개의 식을 통해 연립방정식 형태로 $c, d$를 구할 수 있습니다.

\[\begin{align} \beta &= c (\beta_q + d) \\ \alpha &= c (\alpha_q + d) \\ \end{align}\]

위 식과 같이 2개의 $\alpha, \beta$식이 있다고 가정하면 다음과 같이 식을 전개할 수 있습니다.

\[\begin{align} c &= \frac{\beta - \alpha}{\beta_q - \alpha_q} \\ d &= \frac{\alpha \beta_q - \beta \alpha_q}{\beta - \alpha} \\ \end{align}\]

이러한 Quantization 과정 거칠 때, floating point $0$ 은 quantization error가 없다고 가정합니다. 이 때, $x = 0$ 을 $x_{q}$ 로 나타내면 다음과 같습니다.

\[\begin{align} x_q &= \text{round}\big(\frac{1}{c} 0 - d\big) \\ &= \text{round}(- d) \\ &= - \text{round}(d) \\ &= - d \\ \end{align}\]

floating point 0을 quantization하였을 때, error가 없다고 가정하기 때문에 (no quantization error) 위 식에서 $-\text{round}d = -d$ 를 만족합니다. 즉, round 연산을 통해서 발생하는 error가 없다고 해석하면 됩니다.
즉, 정리하면 quantization은 floating point 0을 기준으로 floating point를 int형으로 변환하는 방법을 의미하고 이 때, floating point 0을 에러가 없다고 가정하여 변환할 때 사용하기 때문에, 임의의 $x$ 를 $x_{q}$ 로 변환할 때에도 기준이 되는 $-d$ 를 사용합니다.
위 식의 $d$ 를 풀어 쓰면 다음과 같은 의미를 가집니다.

\[\begin{align} d &= \text{round}(d) \\ &= \text{round}\big(\frac{\alpha \beta_q - \beta \alpha_q}{\beta - \alpha}\big) \\ \end{align}\]

Quantization을 나타낼 때, 관습적으로 위 식에서 $c$ 는 scale $s$ 로 나타내고 $-d$ 는 zero point $z$ 로 나타냅니다.
정리하면 de-quantization과 quantizaton과 $s, z$는 다음과 같이 나타낼 수 있습니다.

\[\text{de-quantization : } x = s (x_q - z)\]
\[\text{quantization : } x_q = \text{round}\big(\frac{1}{s} x + z\big)\]
\[\begin{align} s &= \frac{\beta - \alpha}{\beta_q - \alpha_q} \\ z &= \text{round}\big(\frac{\beta \alpha_q - \alpha \beta_q}{\beta - \alpha}\big) \\ \end{align}\]

위 식에서 $z, x$ 각각의 의미를 살펴보면 $z$ 는 integer 이고 $s$는 positive floating point입니다.

만약 quantization을 하였을 때, 범위를 $[\alpha, \beta] \to [\alpha_q, \beta_q]$ 로 한정하려고 한다면, Quantization할 때, 범위를 벗어난 $x$ 의 값을 잘라버리는 (clipping) 방식을 취할 수 있습니다.
quantization 하는 범위가 음의 정수를 포함하는 경우와 그렇지 않은 경우를 나누어서 생각하면 다음과 같습니다.

\[\text{int-b : } (\alpha_q, \beta_q) = (-2^{b-1}, 2^{b-1}-1)\]
\[\text{unsigned int-b : } (\alpha_q, \beta_q) = (0, 2^{b}-1)\]

위 제한된 범위에만 $x$ 가 $x_{q}$ 로 변환될 수 있도록 값을 자르는 방식을 value clipping이라고 하면 과정은 다음과 같습니다.
먼저 함수 clip을 정의하면 다음과 같습니다.

\[\begin{align} \text{clip}(x, l, u) &= \begin{cases} l & \text{if $x < l$}\\ x & \text{if $l \leq x \leq u$}\\ u & \text{if $x > u$}\\ \end{cases} \end{align}\]

\[x_q = \text{clip}\Big( \text{round}\big(\frac{1}{s} x + z\big), \alpha_q, \beta_q \Big)\]

이와 같은 방식으로 Quantization하는 방식을 Affine Quantization Mapping 이라고 합니다.

다른 Quantization 방식으로 Scale Quantization Mapping이 있습니다. 앞에서 살펴본 방식과 유사합니다. 다만, 2가지 조건이 추가됩니다.
① 만약 Quantization 시 floating point를 integer로 다음과 같은 범위로 변환한다고 가정해 보겠습니다.

\[(\alpha_q, \beta_q) = (-2^{b-1} + 1, 2^{b-1}-1)\]

② 앞에서 사용한 zero-point를 0으로 가정하겠습니다.

\[z = 0\]

①, ②번 조건에 의하여 다음을 만족해야 합니다.

\[\begin{gather} \alpha_q = -\beta_q \\ \text{round}\big(\frac{\beta \alpha_q - \alpha \beta_q}{\beta - \alpha} \big) = 0 \\ \end{gather}\]

위 식의 조건을 상시 만족하려면 $\alpha = -\beta$ 를 만족해야 함을 알 수 있습니다. 즉, Scale Quantization Mapping의 목적이 제약조건 하에서 $[\alpha, \beta] = [\alpha, -\alpha] \to [\alpha_{q}, \beta_{q}] = [\alpha_q, -\alpha_q]$ 로 변환하는 것입니다.
이와 같은 방식으로 표현하였을 때, Quantization 결과는 0을 기준으로 대칭되도록 나타내어집니다. 이러한 특성으로 인하여 symmetric quantization mapping이라고도 부릅니다.

앞에서 설명하였듯이 scale quantization mapping은 affine quantization mapping의 특수한 한가지 방법에 해당합니다.

지금까지 Quantization mapping의 주요 방법인 Affine Quantization Mapping과 이 방법 중의 하나인 Scale Quantization Mapping에 대하여 살펴보았습니다. 가장 핵심이 되는 Affine Quantization Mapping의 방법의 식을 다시 한번 살펴보면서 다음 내용으로 넘어가겠습니다.

\[\text{quantization : } f_q(x, s, z) = \text{clip}\Big( \text{round}\big(\frac{1}{s} x + z\big), \alpha_q, \beta_q \Big)\]
\[\text{de-quantization : } f_d(x_q, s, z) = s (x_q - z)\]

Quantized Matrix Multiplication 이란

지금까지 임의의 값(스칼라 값)에 대하여 Affine Quantization Mapping이란 방법을 이용하여 Quantization을 하는 방법에 대하여 알아보았습니다.
머신러닝 / 딥러닝에서 다루는 데이터는 최소 Matrix이며 Tensor 범위까지 늘어나기 때문에 가장 기본이 되는 Matrix에서의 Quantization이 어떻게 적용되는 지 살펴보도록 하겠습니다.

먼저 다루어 볼 식은 $Y = XW + b, \text{where, } X \in \mathbb{R}^{m \times p}, W \in \mathbb{R}^{p \times n}, b \in \mathbb{R}^{n}, Y \in \mathbb{R}^{m \times n}$ 의 조건을 가지며 정리하면 다음과 같습니다.

\[\begin{align} Y_{i, j} = b_j + \sum_{k=1}^{p} X_{i,k} W_{k,j} \end{align}\]

위 식에서 $Y_{i, j}$ 를 계산하기 위하여 연산되는 행렬 $X, W$ 의 사이즈는 각각 (i, p)와 (p, j)를 가지고 최종적으로 (i, j) 크기의 행렬 $Y_{i, j}$ 을 만들어 냅니다.
즉, $Y_{i, j}$ 행렬에서 원소 하나의 값을 구하기 위하여 $p$ 번의 floating point 곱 연산과 합 연산이 필요 합니다. 따라서 전체 행렬 $Y_{i, j}$ 을 계산하기 위해서는 $m \times p \times n$ 번의 floating point 곱 연산과 합 연산이 필요합니다.

앞에서 계속 다루어 온 것 처럼 floating point를 이용하여 많은 양의 곱과 합 연산이 발생하면 계산 속도가 느려집니다. 물론 어떤 precision 만큼 사용하느냐에 따라 달라질 수 있지만, integer에 비해서는 계산 속도가 느리기 때문에 위에서 사용한 $Y_{i, j}$ 을 어떻게 Quantization하는 지 살펴보고 이 방법을 통하여 행렬에서의 Quantization 방법을 이해해 보도록 하겠습니다.

먼저 전개되는 수식은 다음과 같습니다.

\[\begin{align} Y_{i, j} &= b_j + \sum_{k=1}^{p} X_{i,k} W_{k,j} \\ &= s_b (b_{q, j} - z_b) + \sum_{k=1}^{p} s_X(X_{q,i,k} - z_X) s_W(W_{q, k,j} - z_W)\\ &= s_b (b_{q, j} - z_b) + s_X s_W \sum_{k=1}^{p} (X_{q,i,k} - z_X) (W_{q, k,j} - z_W)\\ &= s_b (b_{q, j} - z_b) + s_X s_W \Bigg[ \bigg( \sum_{k=1}^{p} X_{q,i,k} W_{q, k,j} \bigg) - \bigg( z_W \sum_{k=1}^{p} X_{q,i,k} \bigg) - \bigg( z_X \sum_{k=1}^{p} W_{q, k,j} \bigg) + p z_X z_W\Bigg]\\ &= s_Y(Y_{q,i,j} - z_Y)\\ \end{align}\]

위 식에서 $X_q, W_q, b_q, Y_q$ 는 $X, W, b, Y$ 각각의 Quantization이 적용된 Matrix입니다. $s_X, s_W, s_b, s_Y$ 는 $X, W, b, Y$ 의 각각의 scale이고 $z_X, z_W, z_b, z_Y$ 는 $X, W, b, Y$ 의 각각의 zero point 입니다.

\[Y_{q,i,j} = z_Y + \frac{s_b}{s_Y} (b_{q, j} - z_b) + \frac{s_X s_W}{s_Y} \Bigg[ \bigg( \sum_{k=1}^{p} X_{q,i,k} W_{q, k,j} \bigg) - \bigg( z_W \sum_{k=1}^{p} X_{q,i,k} \bigg) - \bigg( z_X \sum_{k=1}^{p} W_{q, k,j} \bigg) + p z_X z_W\Bigg]\]

위 식에서 다음 4가지 성분은 inference 시 상수값이므로 inference 하기 전에 미리 구해놓으면 효율적으로 계산할 수 있습니다.

\[z_Y\]
\[\frac{s_b}{s_Y} (b_{q, j} - z_b)\]
\[z_X \sum_{k=1}^{p} W_{q, k,j}\]
\[p z_X z_W\]

위 식과 같이 $Y_{q, i, j}$ 를 정리하였을 때, $\sum_{k=1}^{p} X_{q,i,k} W_{q, k,j}$ 는 integer의 곱과 합으로 나타나지며 이러한 integer matrix multiplication은 다양한 하드웨어에서 자체적으로 연산 최적화 방법을 제시합니다.

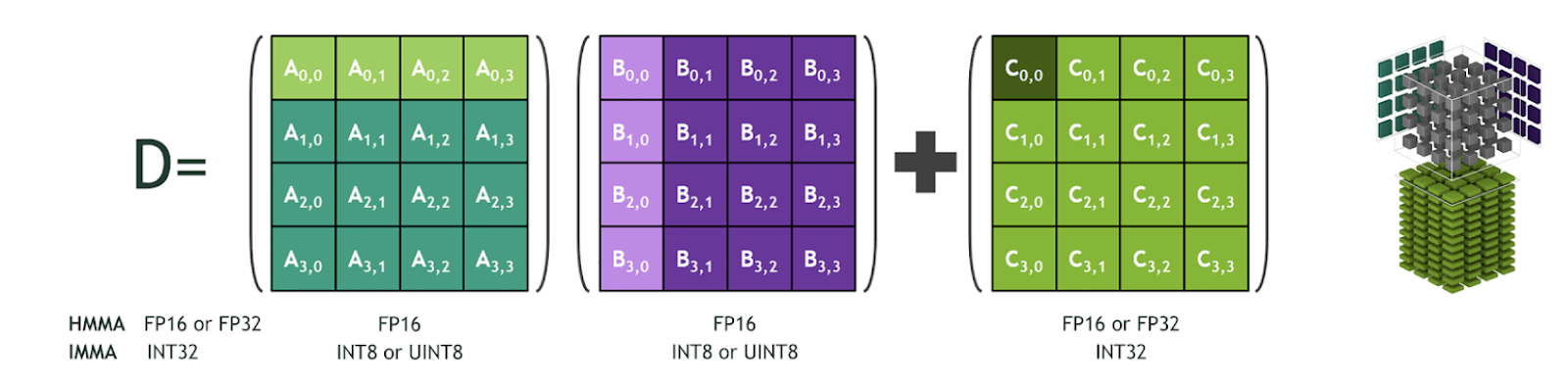
NVIDIA에서는 NVIDIA Tensor Core 또는 Tensor Core IMMA Operation을 지원하며 이 방법을 이용하면 기본적인 matrix multiplication 보다 더 빠르게 계산을 할 수 있습니다. (위 그림은 NVIDIA Tensor Core Operations과 관련된 그림입니다.)

Quantized Deep Learning Layers

Pytorch를 이용한 Static Quantization 실습

(작성중)

Pytorch를 이용한 Sementic Segmentation의 Static Quantization 실습

코드 링크 : static quantization for sementic segmentation
앞의 예제를 통하여 Static Quantization의 간단한 예제를 살펴보았습니다. 이번에는 static quantization을 semantic segmentation에 적용하는 예제를 통하여 실제 사용하는 예제에는 어떻게 적용하는 지 살펴보도록 하겠습니다.

Post Training Quantization과 Quantization Aware Training 비교

이번에는 QAT(Quantization Aware Training)에 대하여 알아보려고 합니다. 그전에 Post Training Quantization과 Quantization Aware Traing에 대한 비교를 통하여 어떤 차이점이 있는 지 차이점을 먼저 비교하여 QAT의 필요성에 대하여 먼저 느껴보도록 하겠습니다.

PTQ(Post Training Quantization) : floating point 모델로 학습을 한 뒤 결과 weight값들에 대하여 quantization하는 방식으로 학습을 완전히 끝내 놓고 quantization error를 최소화 하도록 합니다.
- 장점 : 파라미터 size 큰 대형 모델에 대해서는 정확도 하락의 폭이 작음
- 단점 : 파라미터 size가 작은 소형 모델에 대해서는 정확도 하락의 폭이 큼
QAT(Quantization Aware Training) : 학습 진행 시점에 inference 시 quantization 적용에 의한 영향을 미리 시뮬레이션을 하는 방식으로 최적의 weight를 구하는 것과 동시에 quantization을 하는 방식을 뜻합니다.
- 장점 : Quantization 이후 모델의 정확도 감소 폭을 최소화 할 수 있음
- 단점 : 모델 학습 이후 추가 학습이 필요함

위 도표는 mobilenet v2와 inception v3에 대하여 기존 성능, QAT, PTQ의 Accuracy 성능에 대하여 나타냅니다.
QAT의 경우 두 모델 모두 성능 하락의 폭이 거의 없다고 말할 수 있습니다.
반면 PTQ의 경우 mobilenet v2에서 큰 성능 하락이 발생하였습니다. 이것이 앞에서 언급한 소형 모델에 대해서는 정확도 하락의 폭이 큰 것에 해당합니다. 하지만 모델의 크기가 큰 inception v3에서는 PTQ에서도 성능 하락이 크지 않는 것도 관측할 수 있습니다.
이와 같이 소형 모델에 대한 성능 하락이 크게 감소하는 이유는 소형 모델에서는 weight 및 layer의 갯수가 작으므로 weight가 가지는 정보의 양이 상대적으로 작다는 것에 원인이 있습니다. 따라서 소형 모델의 경우 여러가지 에러 및 outlier의 상황에 민감해 지는데, Quantization으로 인하여 학습을 통해 얻은 실제 weight와 달라지는 경우 그 영향이 더욱 커져서 PTQ에 의한 성능 감소가 더 크게 발생할 수 있습니다.
특히 Quantization을 해야 하는 상황은 Edge device와 같은 환경에서 사용해야하는 경우가 많은데 이 경우 소형 모델을 사용해야 하므로 PTQ를 이용하면 좋은 Quantization 성능을 기대하기 어렵습니다.
따라서 학습을 하면서 Quantization을 시뮬레이션하는 QAT를 이용하여 Quantization으로 인하여 학습을 통해 얻은 실제 weight와 달라지는 상황을 최소화 하는 작업이 필요합니다. 이러한 이유로 소형 모델에서는 특히 QAT가 필수적이라고 말할 수 있습니다.

다음으로 간략하게 구조적으로 PTQ와 QAT의 구조적인 차이점을 살펴보겠습니다.

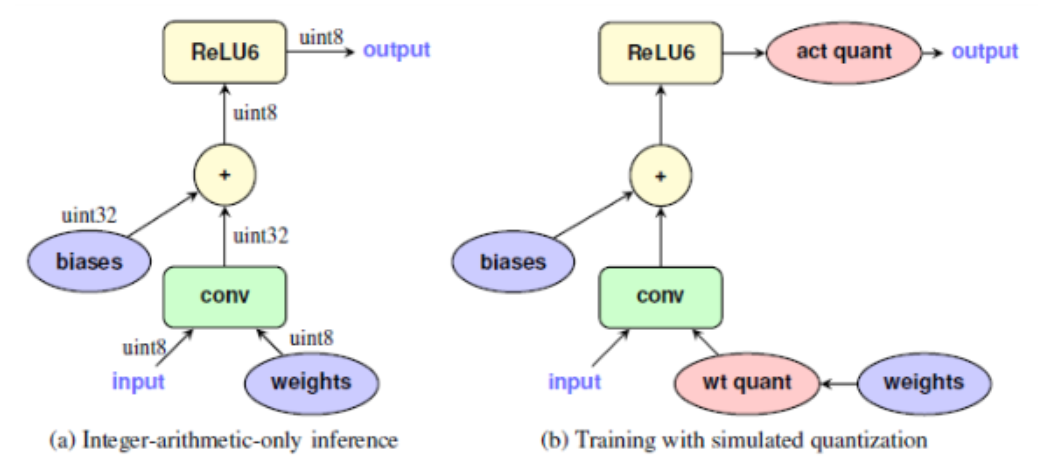
위 그림에서 왼쪽 (a)는 단순히 int형으로 quantization하여 사용하는 방식이고 오른쪽 (b)는 QAT를 사용한 방식입니다.
(b)를 보면 빨간색에 해당하는 act quant (activation quantization)과 wt quant (weight quantization)이 추가된 것을 확인할 수 있습니다.
앞에서 설명하였듯이 QAT는 forward / backward 에서 weight와 activation function 출력에 대한 quantization을 학습 중에 시뮬레이션 합니다.
위의 빨간색 노드를 fake quantization node라고 하며 forward / backward pass에서 quantization 적용 시의 영향을 시뮬레이션하게 됩니다.
추가적으로 batch normalization은 inference에 사용되는 모드를 적용하여 시뮬레이션을 하게 됩니다.

QAT (Quantization Aware Training) 방법

static quantization 을 통하여 inference 중에 매우 효율적인 quantized된 int형 모델을 만들 수 있습니다.
하지만 post-training calibration을 하더라도 모델의 정확도가 감소할 수 있고 때때로 감소의 폭이 커서 큰 성능 하락이 발생할 수도 있습니다.
이러한 경우 post-training calibration 만으로는 quantized int형 모델을 만드는 데 충분하지 않을 수 있으므로 QAT(Quantization Aware Training)를 사용해 보고자 합니다. QAT는 학습 중에 quantization 효과를 모델링 할 수 있습니다.

QAT의 메커니즘은 간단합니다. floating point 모델에서 quantized된 정수 모델로 변환하는 동안 quantized가 발생하는 위치에 fake quantization module, 즉 quantization 및 dequantization 모듈을 배치하여 integer quantization에 의해 가져오는 클램핑 및 반올림의 효과를 시뮬레이션합니다.
fake quantization 모듈은 scale과 weight 및 activation의 zero-point를 모니터링합니다.
QAT가 일단 끝나면 floating point 모델은 fake quantization 모듈에 저장된 정보를 사용하여 quantized integer model로 변환될 수 있습니다.

이와 같은 방법은 마치 fine-tuning을 하는 것과 같습니다. quantization은 Floating Point 형태로 학습된 파라미터를 그대로 사용하지 못하고 Floating Point가 Int 형으로 바뀜으로써 파라미터 값에 변화가 생기기 때문에 이와 같은 문제를 fine-tuning 방법으로 개선하고자 하는 것입니다.

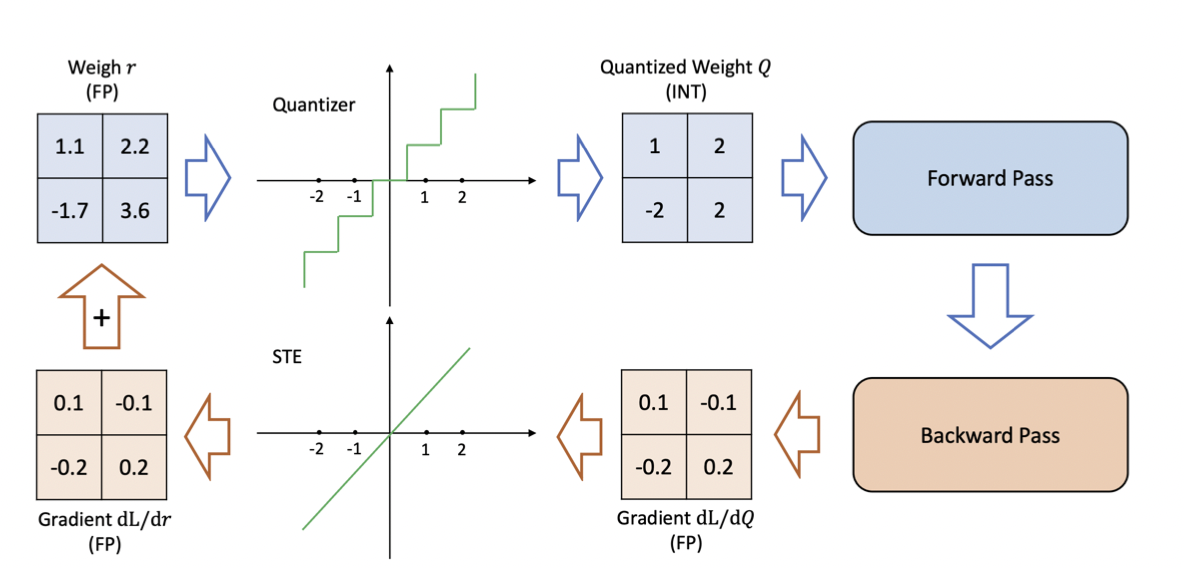
Quantization Aware Training을 할 때에는 위 그림과 같은 절차를 통하여 weight 학습이 됩니다.
먼저 위 그림에서 파란색 부분은 지금까지 살펴보았던 내용입니다. 학습된 Floating Point형의 Weight를 Quantization 합니다. 핵심은 학습 중에 시도해 본다는 것입니다. 그 다음에 Forward Pass를 진행합니다.
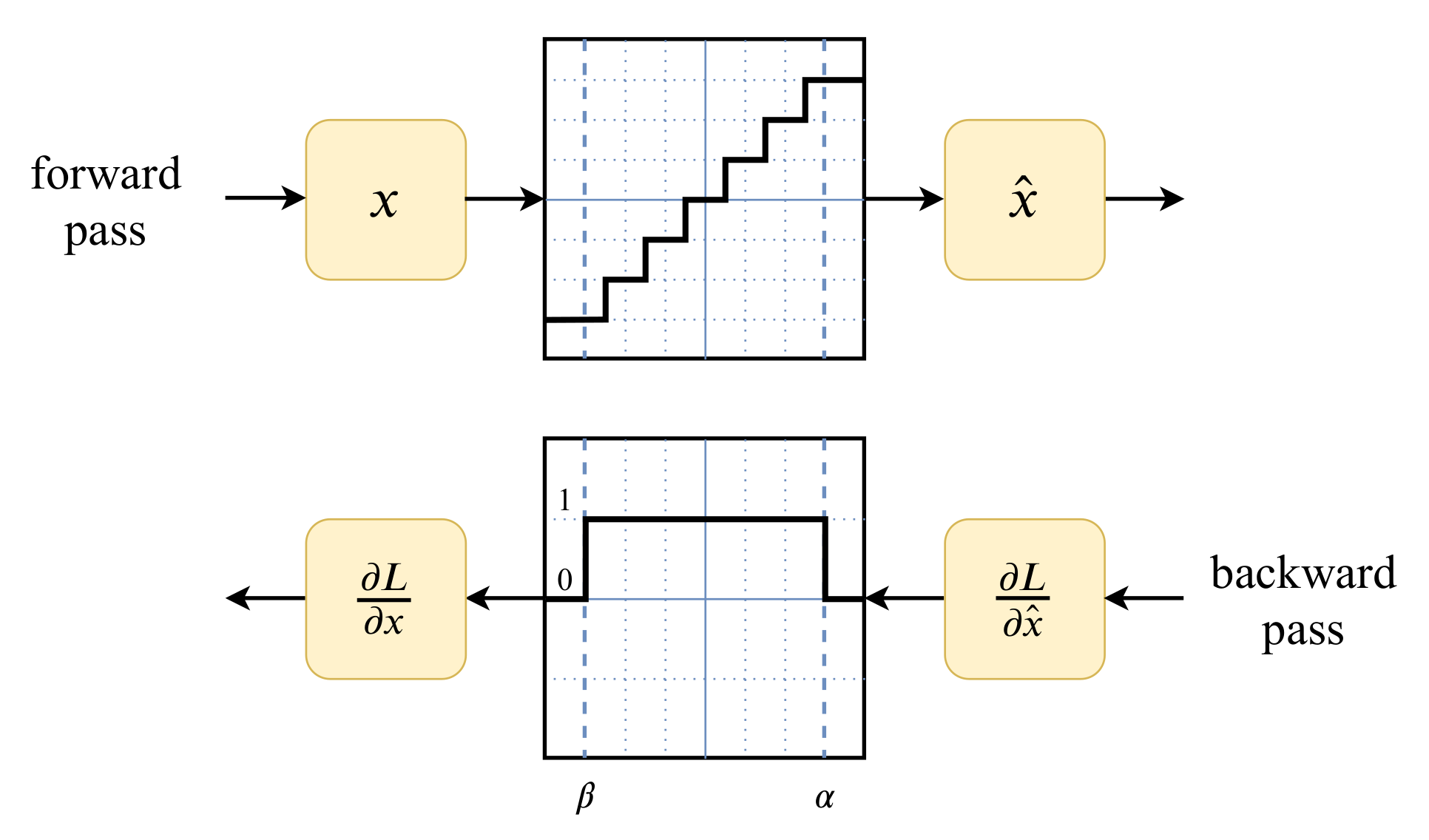
그 다음 Backpropagation이 진행될 때, Quantized 된 Weight Q 에 대하여 gradient를 구합니다. gradient 값은 Floating Point 형태로 나오게 됩니다. STE(Straight Through Estimator) (논문 참조 : Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation) 를 통하여 Quantized 된 영역을 다시 straight 하게 만들어 주고 실제 weight 반영은 Weight r에 대하여 진행합니다.
즉, 최초 Gradient는 dL/dQ (FP)를 이용하여 구하지만 실제 back propagation 할 때에는 dL/dr (FP)가 될 수 있도록 환경을 재구성하는 것입니다.

QAT를 진행하기 위해서 Pytorch에서 어떻게 사용하면 될 지 알아보도록 하겠습니다. 아래 코드에서 살펴볼 예제는 FP32 → INT8 형태로 quantization 하는 예제입니다. 절차는 다음과 같습니다.
①

deep learning 관련 글 목차