Transposed Convolution을 이용한 Upsampling
2019, Feb 12
- 참조 : https://medium.com/activating-robotic-minds/up-sampling-with-transposed-convolution-9ae4f2df52d0
목차
-
Upsampling의 필요성
-
Transposed Convolution의 사용 이유
-
Convolution Operation
-
Going Backward
-
Convolution Matrix
-
Transposed Convolution Matrix
-
Transposed Convolution의 문제점
Upsampling의 필요성
- 딥러닝 학습을 할 때, 낮은 해상도의 feature를 높은 해상도의 feature로 만들어 줄 때 Upsampling 연산이 필요합니다.
- upsampling 할 때, 많이 사용하는 방법이
interpolation이고 그 중Nearest neighbor interpolation,bilinear interpolation,bicubic interpolation등이 대표적인 interpolation 방법입니다. - 이 중 어떤 interpolation 방법을 사용할 지 정하는 것은 사용자의 몫입니다. 위 interpolation 방법들은 기존 픽셀값들 만으로 해상도를 늘리는 방법들이므로 새로운 파라미터를 학습할 것이 없습니다. 즉, 학습과 무관한 연산입니다.
Transposed Convolution의 사용 이유
- 만약 딥러닝 네트워크가 네트워크 목적에 맞도록 최적화하여 Upsampling을 하도록 하려면
Transposed Convolution을 사용할 수 있습니다. 이 방법은 앞에서 설명한 interpolation과 다르게 학습할 수 있는 파라미터가 있는 방법입니다. - Transposed Convolution을 사용하는 대표적인 문제는 semantic segmentation 입니다.
- Semantic segmentation은 convolution layer를 사용하여 인코더에서 기능을 추출한 다음 디코더에서 원래 이미지 크기를 복원하여 원본 영상의 모든 픽셀을 분류할 수 있도록 합니다. 이 떄, 디코더에서 원래 이미지 크기를 복원할 때, 대표적으로 interpolation이 사용되고 같은 이유로 Transposed Convolution이 사용될 수 있습니다.
- 논문에 따라서 Transposed Convolution은 Fractionally-strided convolution 또는 Deconvolution으로도 불립니다. 이 글에서는 Transposed Convolution으로 적겠습니다.
Convolution Operation
- 먼저 Convolution 연산에 대하여 살펴보도록 하겠습니다.
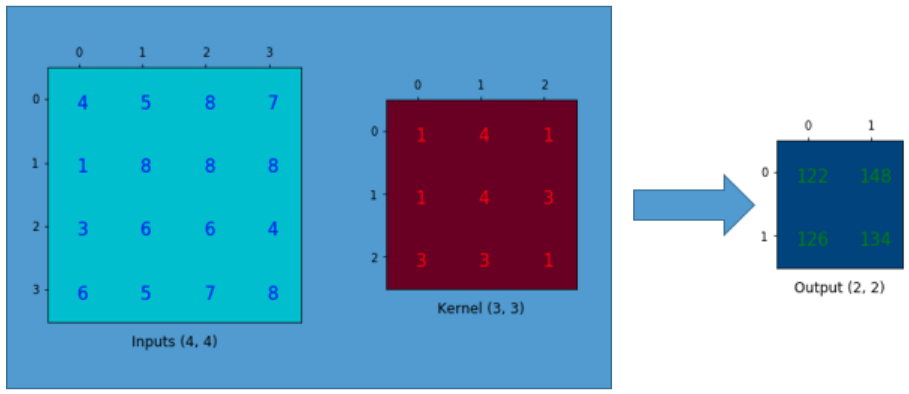
- 위 그림과 같이 4 x 4 크기의 행렬에 3 x 3 크기의 커널을 이용하여 convolution 연산 (padding = 0, stride = 1)을 한다고 가정해 보겠습니다. 그러면 위 그림의 오른쪽과 같이 2 x 2 크기의 행렬이 결과값으로 도출됩니다.
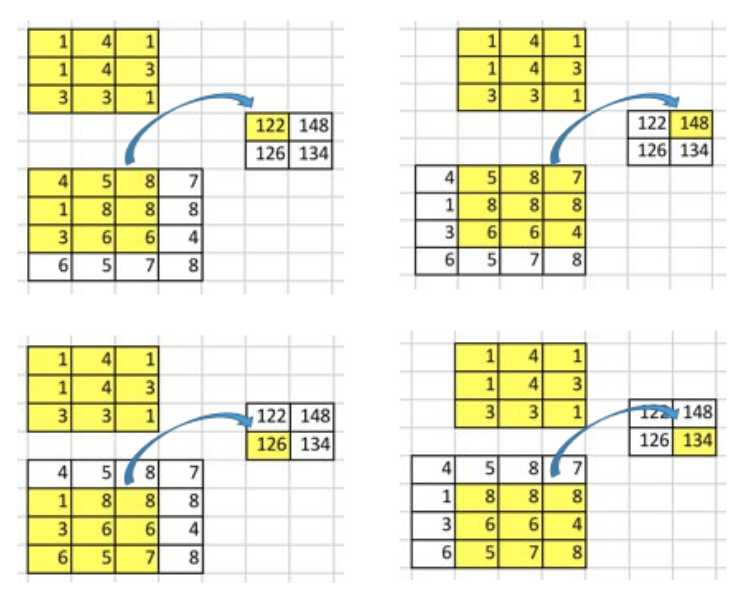
- 연산 과정을 살펴 보면 위 표와 같이 2 x 2 즉, 4번의 convolution 연산을 거치게 됩니다. 각 연산은 element-wise multiplication을 거칩니다.
- convolution 연산에서 중요한 점은 입력값과 출력간의 위치의 연관성이 있다는 것입니다. 예를 들어 위 예제에서 입력값 중 왼쪽 상단의 영역에서 convolution 연산을 한 결과는 출력값 또한 왼쪽 상단의 영역에 대응됩니다.
- 또한 convolution 연산은 다대일(many-to-one) 관계를 가집니다. 위 예제와 같은 3 x 3 커널의 convolution 연산은 9개의 입력값이 1개의 출력값에 대응됩니다.
Going Backward
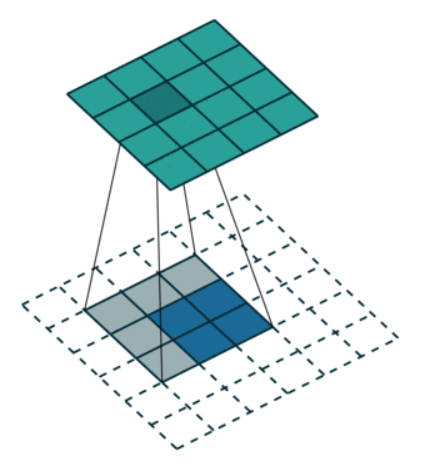
- 반면 Transposed Convolution은 입력값의 크기가 더 작고 출력값의 크기가 더 커져야 하는 구조입니다.
- 즉, 일대다(one-to-many) 관계를 가져야 하므로 convolution 연산과 완전히 반대 형태가 됩니다.
- 앞의 예제에서는 4x4 행렬이 convolution 연산을 통해 2x2 행렬이 되었습니다. 그러면 반대로 2x2 행렬을 4x4행렬로 만들어 보겠습니다.
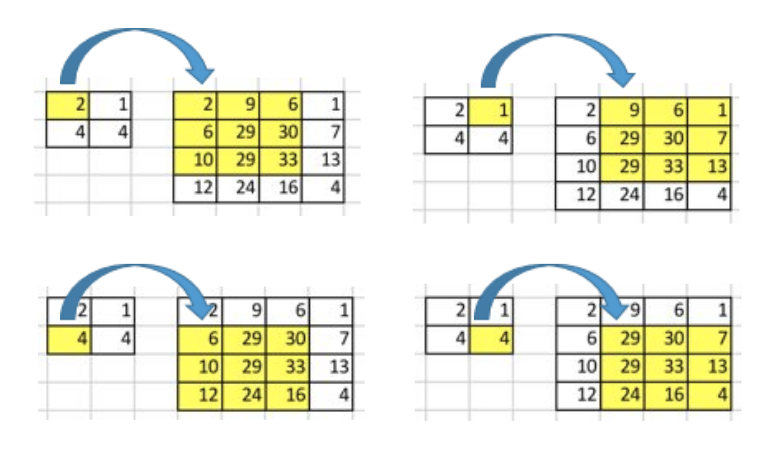
- 위 그림 처럼, 2x2 행렬을 4x4 행렬로 upsampling 할 수 있습니다. 이 경우 1 대 9 즉, 일대다 관계를 가지게됩니다.
- 그러면 위 연산은 어떻게 이루어 지는 것일까요?
Convolution Matrix
- 먼저 convolution 행렬에 대하여 살펴보도록 하겠습니다.

- 앞에서 다룬 3x3 커널의 convolution 연산을 하나의 행렬로 나타낸다면 다음과 같이 4 x 16 행렬로 나타낼 수 있습니다.

- 위 행렬은 3x3 커널의 convolution 연산을 행렬 하나로 표현하기 위해 재정렬한 것입니다. (뒤에서 예제를 보면 이해하는 데 도움이 되니 참조하시기 바랍니다.)
- 위 행렬의 각 행은 convolution 연산을 나타내며 실제 convolution 연산이 되지 않는 위치는 0으로 채웁니다.
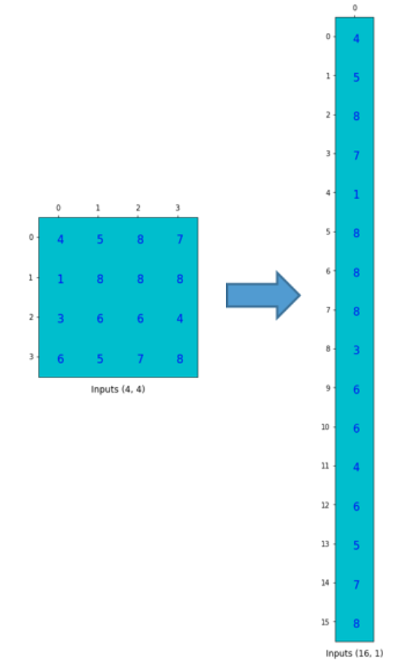
- 그리고 위 그림과 같이 convolution 연산을 할 입력값을 벡터로 만들어 줍니다.
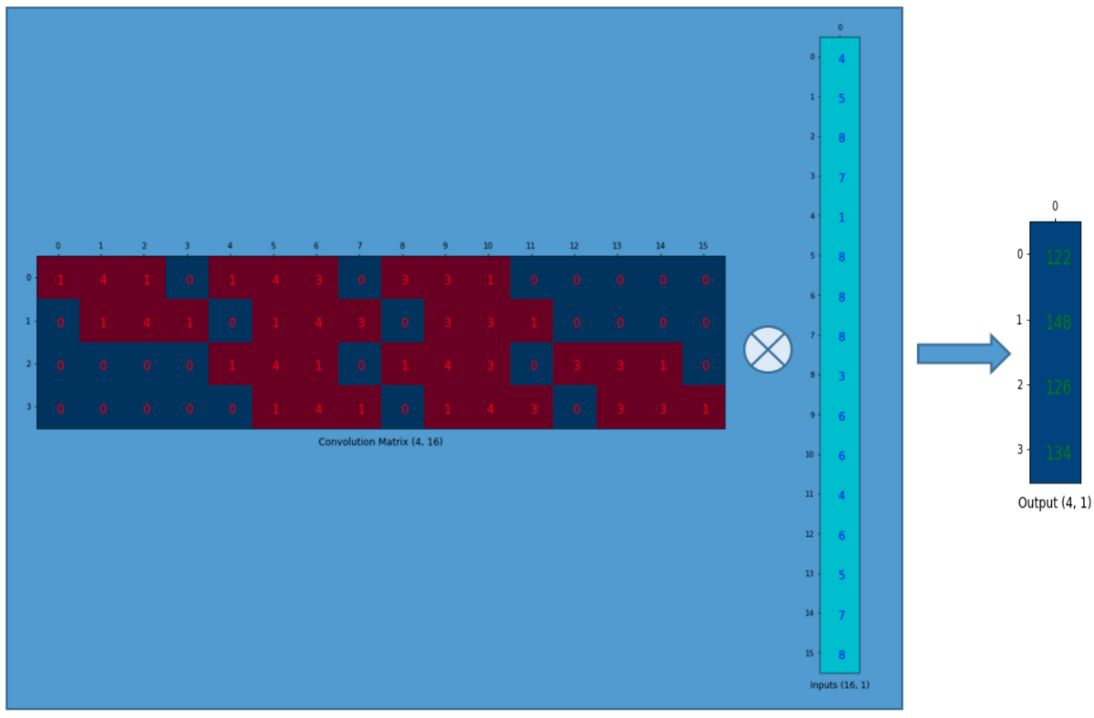
- 그러면 위 그림과 같이 4 x 16 형태의 커널과 벡터 형태의 입력을 행렬 곱을 통하여 계산할 수 있습니다.
- 위 연산은 convolution 연산을 단순 행렬 곱으로 함축하여 표현한 것입니다.

- 행렬 곱 연산 결과 4개의 원소 값을 가지는 벡터가 도출되었고 이는 2 x 2 행렬로 나타낼 수 있습니다.
- 이런 방식으로 설명을 드린 이유는 convolution 연산은 단순히 커널의 weight 값들을 재배열한 후 행렬 곱을 한 것임을 설명하기 위함이었습니다.
- 구체적인 수치로 설명하면 위 예제에서 convolution 연산은 4 x 16 크기의 convolution matrix를 통하여 16 (4 x 4) 크기의 벡터가 4 (2 x 2) 크기의 벡터로 변환된 것입니다.
- 그러면 반대로 convolution matrix의 크기가 16 x 4 라면 크기가 4인 벡터가 크기가 16인 벡터로 변환될 것입니다. 이것이 핵심입니다.
Transposed Convolution Matrix
- Transposed Convolution Matrix는 앞에서 든 예와 같이 16 x 4 크기를 가져야 합니다. 추가적으로 더 확인해 볼 것은 Transposed Convolution에서 가지는 일대다 관계를 가지는 지 확인 해보겠습니다. 위 예제에서는 1 대 9 관계를 가져야합니다.
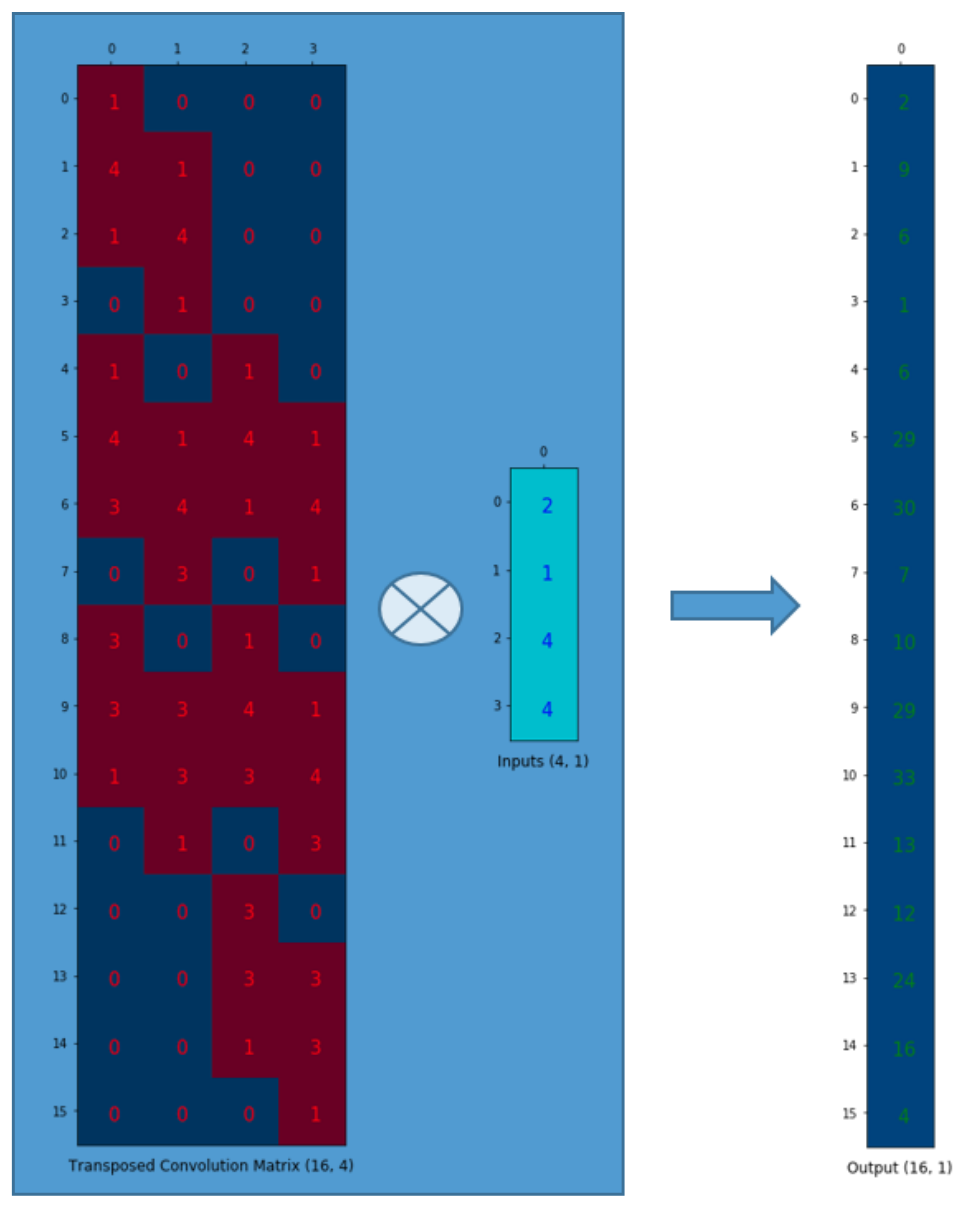
- 위 그림을 보면 크기 4인 벡터를 Transposed Convolution Matrix와 행렬 곱을 통하여 크기 16인 벡터를 생성한 것을 볼 수 있습니다.
- 특히 각 열 기준으로 각 열 당 9개의 빨간색 사각형을 통해 1 대 9 관계 즉, 일대다 관계가 성립하는 것 을 알 수 있습니다. 앞의 convolution matrix와 마찬가지로 연산이 되지 않는 영역은 0으로 채웠습니다.
- 위 예제의 convolution matrix와 transposed convolution matrix의 값은 각각 학습을 통해 만들어 지는 값들이므로 임의로 정할 필요가 없습니다.
- 따라서 위와 같은 방법으로 transposed convolution은 convolution 연산과 유사하게 학습할 수 있는 파라미터를 통하여 연산을 합니다. 그리고 그 연산의 목적이 Upsampling으로 Upsampling이 잘 되는 방향으로 파라미터는 학습을 하게 됩니다.
Transposed Convolution의 문제점
- 분석적으로(Analytically) 접근하는 interpolation 방법 대신 학습할 수 있는 (learnable) 방법으로 접근하는 transposed convolution에도 발생하는 문제가 있습니다.
- 소위 말하는 checkboard artifact가 그 문제입니다.

- 위 그림을 보면 출력의 형태가 체크보드와 같은 인공물 처럼 나오는 것을 확인할 수 있습니다.
- 위 checkboard artifact 링크를 참조하면 interpolation을 이용한 Upsampling + Convolution 조합으로 문제를 개선할 수 있음을 알 수 있습니다. 자세한 내용은 링크를 참조하시기 바랍니다.
- 따라서 Upsampling을 많이 사용하는 Generative 모델이나 세그멘테이션 모델에서 Transposed Convolution 대신에
interpolation + convolution조합을 대신 사용하여 해상도 증가는 interpolation으로 하면서 동시에 학습할 수 있는 구조를 만들어 냅니다.