Deep Learning에서의 Uncertainty 관련 내용 정리

deep learning 관련 글 목차

참조 : https://www.edwith.org/bayesiandeeplearning/
참조 : https://www.youtube.com/watch?v=d7y42HfE6uI
참조 : https://www.youtube.com/watch?v=bWfjoOsHT_Y&list=WL&index=103&t=1s
참조 : https://www.youtube.com/watch?v=YaEP_k3JZ8Q&list=WL&index=105&t=1065s

이번 글에서 다룰 내용은 Deep Learning의 Uncertainty와 관련된 내용에 대하여 살펴보겠습니다.
먼저 Uncertainty를 다루기 위해서는 Bayesian Neural Network에 관한 개념이 필요합니다. (상세 내용은 링크를 통하여 참조하시기 바랍니다.) 간단하게 개념을 소개하면 variational distribution을 찾는 것이 목적인 뉴럴 네트워크 이고 variational distribution은 뉴럴 네트워크의 파라미터를 샘플링 하는 것이라고 말할 수 있습니다.
즉, 뉴럴 네트워크의 정해진 파라미터를 통해 같은 입력 값에 대하여 같은 출력을 내는 것이 아니라 샘플링을 통하여 파라미터 값을 조금씩 변경하여 확률처럼 보일 수 있도록 하는 것입니다. 이 점을 기억하면서 Uncertainty에 관한 내용들을 살펴보도록 하겠습니다.

Uncertainty in Deep Learning

논문 링크 : Uncertainty in Deep Learning, Yarin Gal

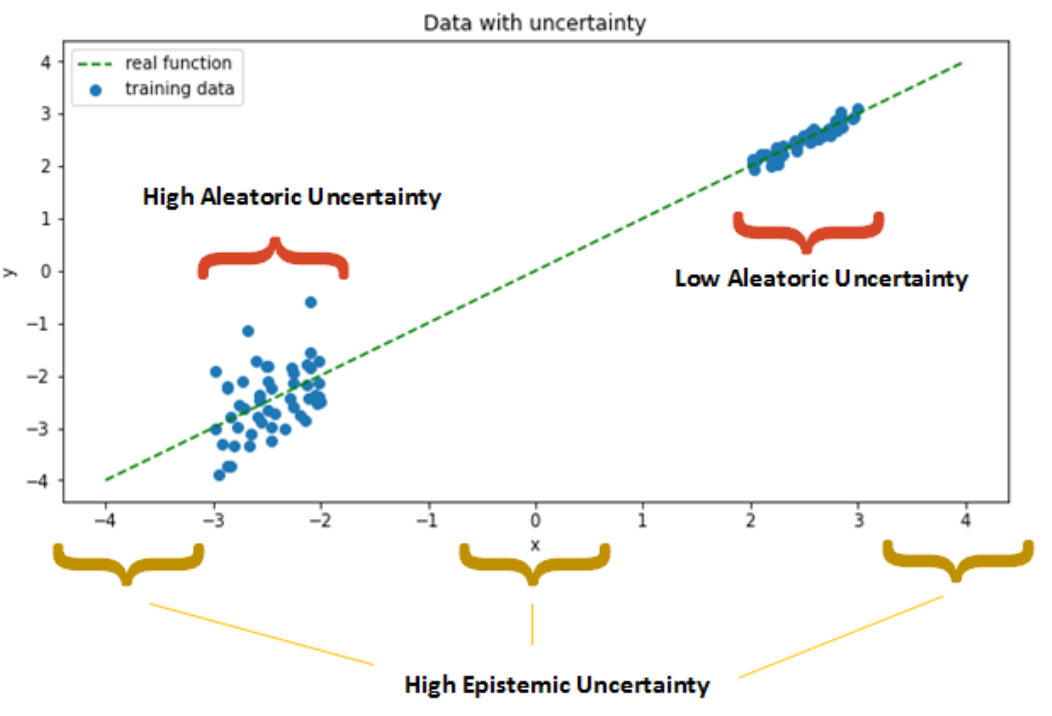
Uncertainty in Deep Learning 논문을 다루기 전에 uncertainty의 유형에 대하여 먼저 알아보도록 하겠습니다. uncertainty는 크게 3가지로 나뉠 수 있습니다.

out of distribution test data : 한번도 학습할 때 사용하지 못한 유형의 데이터가 테스트 시 사용되는 경우를 말합니다. 예를 들어 여러 개의 개 품종 사진으로 훈련된 모델이 주어졌을 때, 모델에게 고양이 사진을 사용하여 개 품종을 결정하도록 요청하는 예시입니다.

uncertainty

aleatoric : 학습 데이터 자체에 노이즈가 많아져서 불확실성이 생기는 경우를 뜻합니다. 예를들어 학습할 때 분류할 세 가지 유형인 고양이, 개, 소가 있다고 가정하겠습니다. 이 때, 고양이 이미지만 노이즈가 있고 개와 소의 이미지는 정상적인 이미지인 경우라면 이 때 발생하는 불확실성을 뜻합니다.

epistemic uncertainty : 주어진 데이터 세트를 가장 잘 설명하는 최상의 모델 매개변수 및 모델 구조의 불확실성을 뜻합니다. 예를들어 어떤 데이터셋에 대하여 아래 3가지 모델 중 어떤 모델이 가장 적합한 모델이 되는 지에 대한 불확실성이라고 말할 수 있습니다.

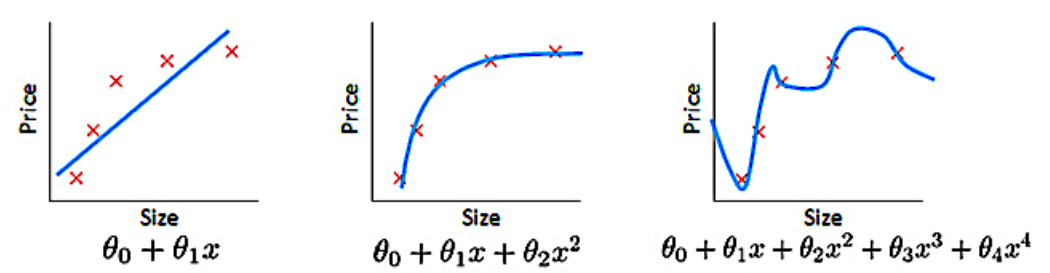
이 논문이 다루는 핵심 내용은 Dropout as a Bayesian approximation 이란 개념입니다. 즉, 모든 레이어에 드랍아웃을 적용하는 것은 베이지안 모델과 동치라는 것입니다.
그 과정을 위해서 variational inference에 사용되는 likelihood를 정의할 때, 가우시안 프로세스를 이용하여 likelihood를 전개합니다.

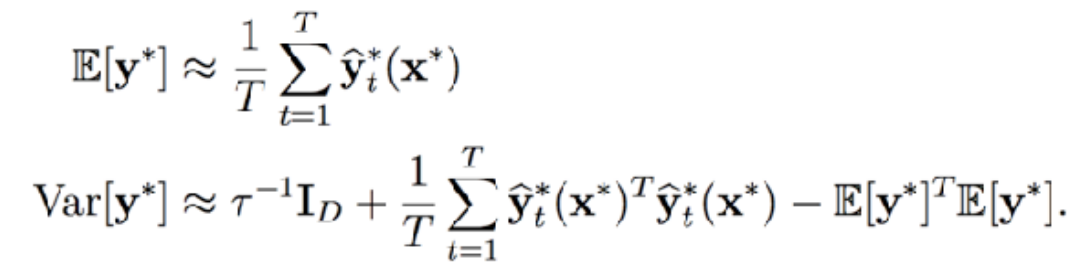
결과적으로는 입력이 고정된 상태에서 뉴럴넷에서 드랍아웃을 적용하여 나오는 서로 다른 결과의 평균과 분산이 \(y^{*}\)로 표현되는 출력값 예측에 대한 평균과 분산과 근사화 된다는 것을 보여줍니다.
이 결과를 살펴보기 위해 단계별로 확인해 보겠습니다.

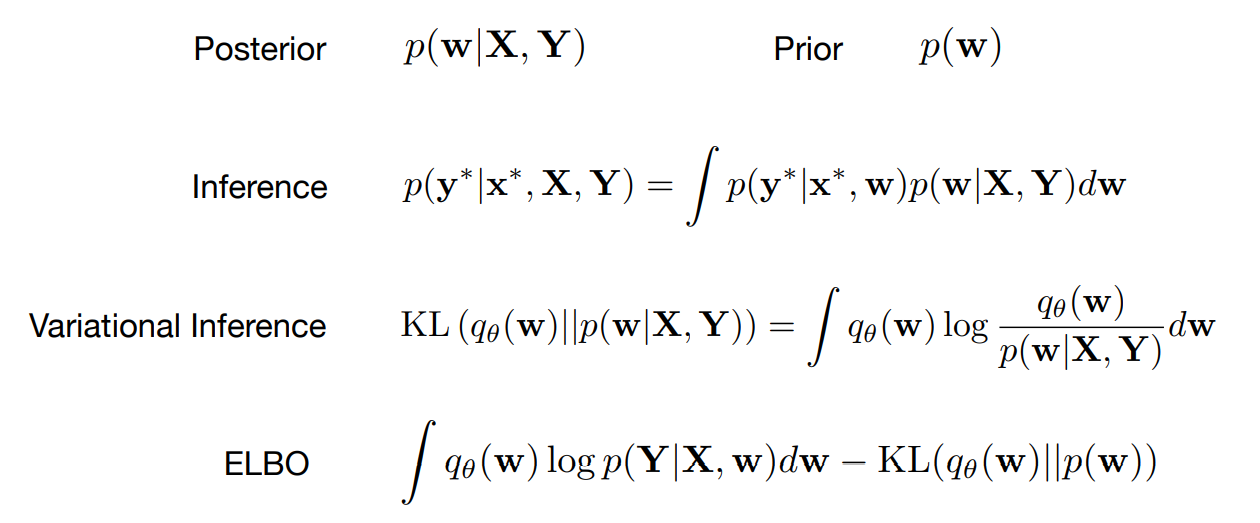
위 식의 의미를 하나씩 살펴보겠습니다.
Prior : \(p(w)\) 즉 파라미터에 대한 확률 분포를 뜻합니다.
Posterior : bayesian inference에서 다루기 힘든 prior distribution에 관한 random variable을 이용하여 posterior distribution을 찾는 것을 목표로 합니다. \(p(w \vert X, Y)\) 는 주어진 데이터 \(X, Y\) 가 있을 때, 파라미터 \(w\) 에 대한 확률 분포를 뜻하며 beysian neural network에서 구하고자 하는 값입니다.
Inference : posterior distribution가 주어져 있고, 파라미터 \(w\) 가 있을 때, 새로운 인풋 \(X, Y\) 에 대한 분포를 찾는 것이 목적이 됩니다. 하지만 Inference 값을 바로 구하기는 어렵습니다. 왜냐하면 posterior distribution이 주어졌을 때에도 정확한 inference는 latent variable에 대한 distribution과 관련하여 적분을 포함하기 때문에 계산을 다루기 어려울 가능성이 매우 높습니다.
Variational inference : \(q_{\theta}\) 라는 variational distribution이 \(p(w \vert X, Y)\) 와 분포가 가깝게 만드는 것을 뜻합니다. 이 때, KL divergence를 최소화하여 두 분포가 가깝다고 판단해야 합니다. 하지만 \(q_{\theta}\) 라는 것을 직접적으로 구할 수는 없습니다.
ELBO (Evidence Lower Bound) : KL divergence를 최소화하는 것은 ELBO를 최대화 하는 것과 같습니다. ELBO는 latent vaiable에 대한 distribution 각각에 대하여 적분하는 의미를 포함하고 있습니다.

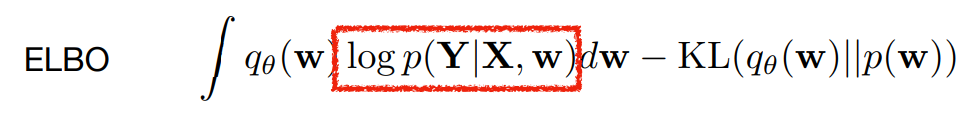
ELBO를 풀 때, 필요한 것은 먼저 likelihood에 해당하는 \(log p(Y \vert X, w)\) 와 prior \(p(w)\) 입니다.
그리고 ELBO를 풀 때, variational distribution에 대한 파라미터를 정의해야 합니다. 많은 경우 \(q_{theta}(w)\) 와 같은 추정해야 하는 분포를 가우시안 분포로 많이 둡니다. 차원이 낮을 때에는 가우시안이 성능도 좋고 간단하기 때문에 좋은 방법일 수 있으나 딥러닝에서의 파라미터는 백만 단위가 넘어갈 수 있기 때문에 백만 차원의 가우시안은 너무 복잡해집니다.
따라서 베르누이 분포 즉, 0과 1에 대한 두 확률 \(p , (1 - p)\) 을 사용하여 뉴럴넷의 수백만개의 파라미터 각각을 사용할 지 유무를 결정할 수 있도록 variational distribution을 근사화 합니다. 즉, variation distribution이 베르누이 분포를 따르도록 합니다. 이러한 형태는 드랍아웃과 동치가 됩니다.
드랍아웃을 적용하는 것이 매번 랜덤하게 행렬에 0 값을 넣고 이 행렬을 네트워크 연산에 적용하여 랜덤하게 특정 레이어 값을 없애는 것을 말합니다. 드랍아웃을 위해 랜덤하게 0을 가지는 행렬을 만드는 것이 \(q_{theta}(w)\) 라고 말할 수 있습니다.
정리하면 베르누이 분포로 부터 랜덤하게 마스킹 행렬을 구하고 이 마스킹과 뉴럴넷의 파라미터 \(w\)를 곱해서 만들어지는 드랍아웃이 적용되는 것이 \(q_{\theta}\) 라는 variational distribution인데 이 값이 ELBO를 통해 근사화되는 posterior이므로 드랍아웃을 적용하는 것은 posterior를 구하는 베이지안 확률 분포가 됩니다.

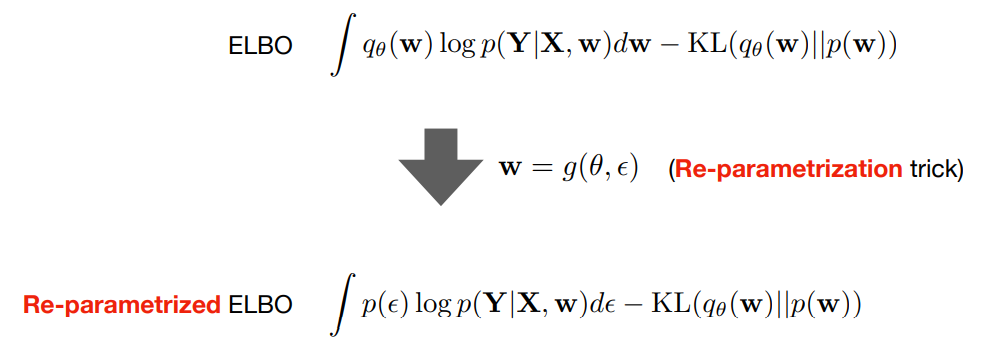
위 식에서 reparametrization trick 부분을 통하여 \(q_{\theta}(w)\) 를 \(p(\epsilon)\) 으로 바꿔서 표현한 것이 드랍아웃을 적용한 것에 해당합니다. 위 식과 같이 reparametrization trick을 통해 드랍아웃을 적용하면 더이상 \(w\)에 대하여 신경쓸 필요없이 \(\epsilon\) 에 해당하는 값인 각각의 뉴럴넷의 파라미터를 사용할 지 사용하지 않을 지(0/1) 그 값만 신경을 쓰면 됩니다.

Uncertainties in Bayesian Deep Learning for Computer Vision

deep learning 관련 글 목차