VAE(Variational AutoEncoder)
2019, Feb 25
- 이번 글에서는 Variational AutoEncoder의 기본적인 내용에 대하여 다루어 보도록 하겠습니다.
목차
-
AutoEncoder의 의미
-
Variational AutoEncoder의 의미
-
Variational AutoEncoder의 상세 내용
-
Variational AutoEncoder의 구현
AutoEncoder의 의미
- AutoEncoder(이하 AE)는 저차원의 representation \(z\)를 원본 \(x\)로부터 구하여 스스로 네트워크를 학습하는 방법을 뜻합니다. 이것은 Unsupervised Learning 방법으로 레이블이 필요 없이 원본 데이터를 레이블로 활용합니다.
- AE의 주 목적은 Encoder를 학습하여 유용한
Feature Extractor로 사용하는 것입니다. 현재는 잘 쓰지는 않지만 기본 구조를 응용하여 다양한 딥러닝 네트워크에 적용 중에 있습니다. (ex. VAE, U-Net, Stacked Hourglass 등등)
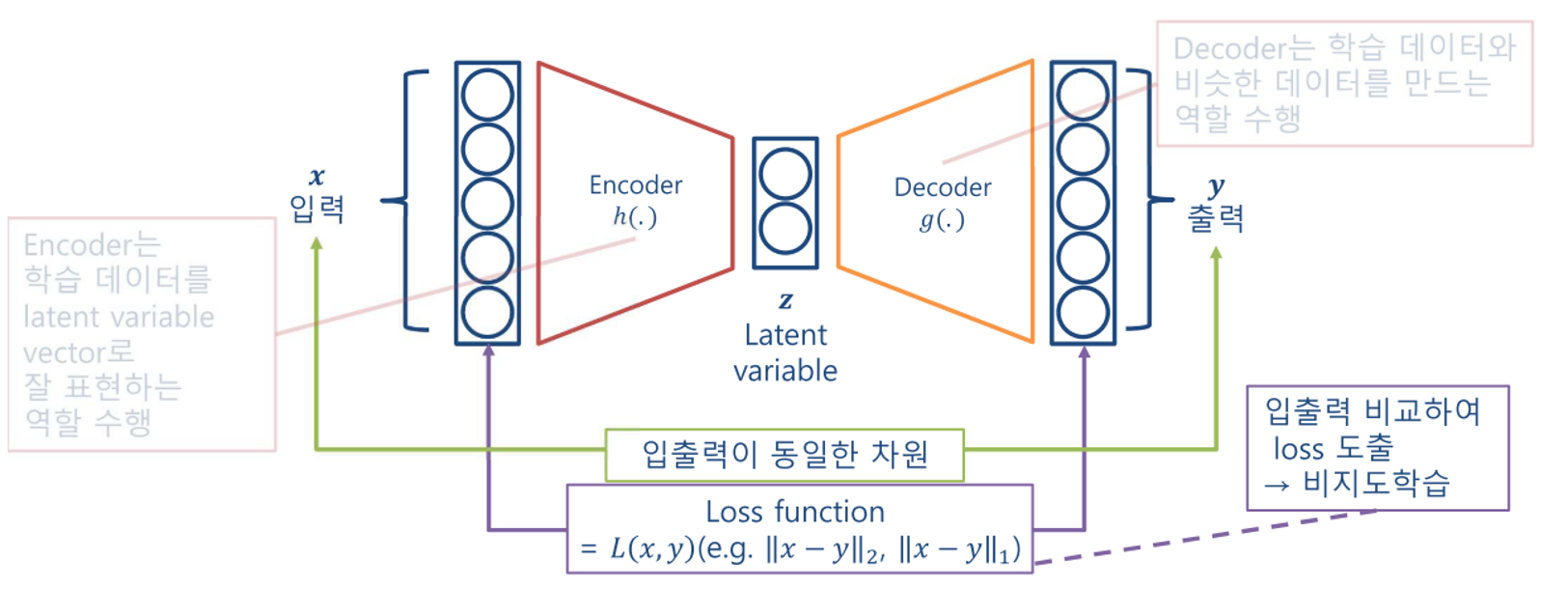
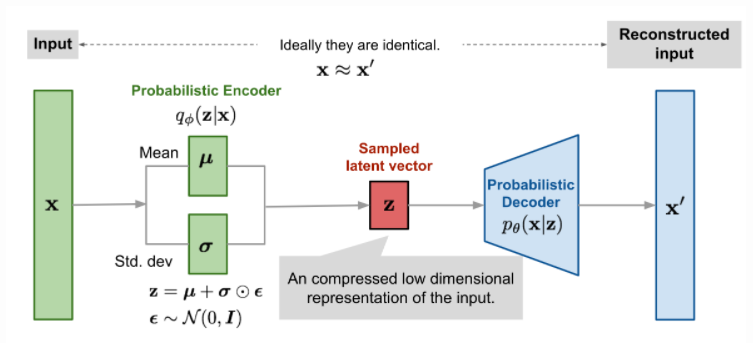
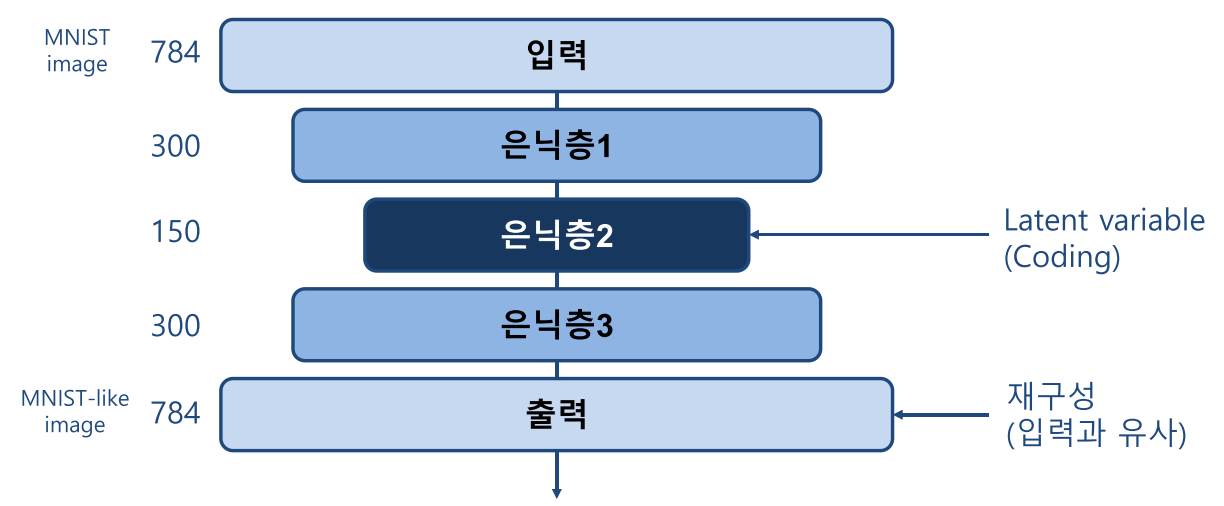
- 먼저 AE의 전체적인 구조는 위 아키텍쳐와 같습니다.
- 입력 \(x\)와 출력 \(y\)가 최대한 동일한 값을 가지도록 하는 것이 AE의 목적이며 입력의 정보를 압축하는 구조를
Encoder라 하고 압축된 정보를 복원하는 구조를Decoder그리고 그 사이에 있는 Variable을Latent Variable\(Z\) 라고 합니다.

- AE에서 저차원 표현 \(z\)는 위 그림과 같이 원본 데이터의 함축적인 의미를 가지도록 학습이 됩니다. 물론 위 예시처럼 물체의 형상, 카메라 좌표, 광원의 정보와 같이 명시적으로 Latent Variable이 저장되지는 않지만 어떤 특징 정보가 저장된다는 점은 일치합니다.
- 이는 다른 머신 러닝 모델에서 feature라 불리는 것과 같은 의미이며 학습 과정에서 겉으로 드러나지 않는 숨겨진 변수이므로
Latent Variable이라고 불리게 됩니다.
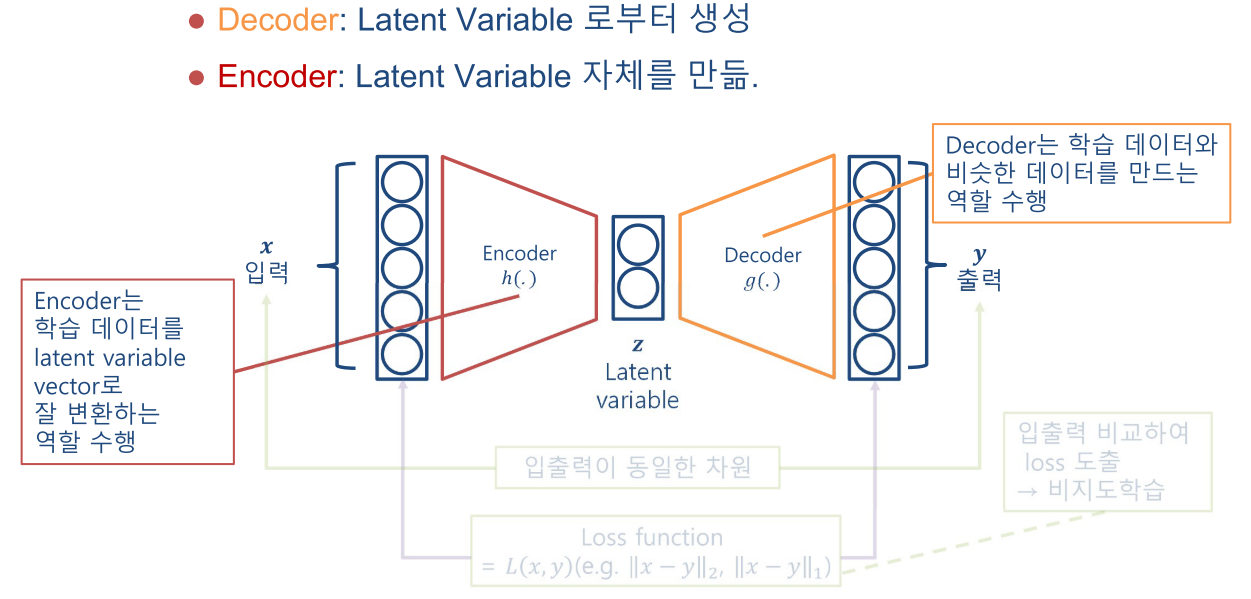
- 따라서 Encoder는 Latent Variable 자체를 만드는 역할을 하고 Decoder는 Latent Variable로 부터 데이터를 생성하는 데 사용됩니다.
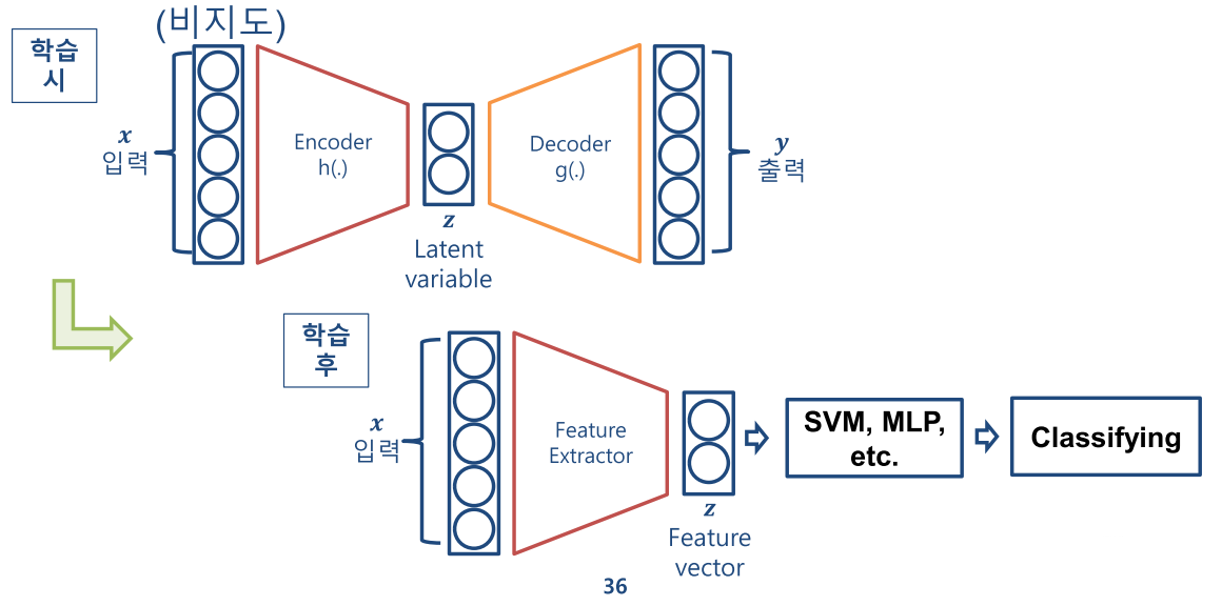
- AE의 Latent Variable은 입력을 압축하여 Feature를 만들기 때문에,
Feature Extractor의 역할을 할 수 있습니다. - 따라서 위 그림과 같이 학습이 완료된 AE에서
Encoder와Latent Variable까지만 가져와 Feature \(Z\)를 추출하고 그 값을 이용하여 다른 머신 러닝 Classifier와 섞어서 사용하곤 하였습니다.
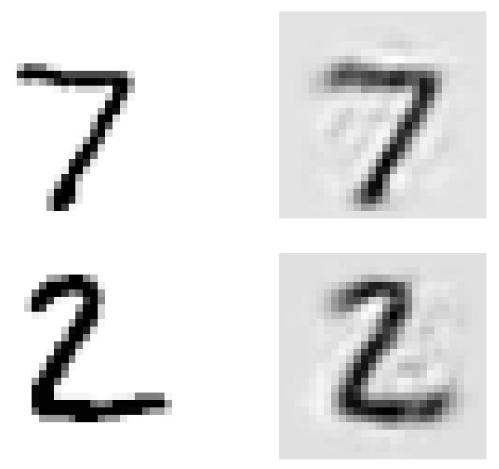
- MNIST 데이터를 이용하여 AE를 사용한 결과 예시는 위와 같습니다. MNIST 데이터로 학습이 완료된 네트워크를 숫자 7, 2 입력을 넣으로 오른쪽의 약간 흐릿하지만 원본과 유사한 데이터가 생성된 것을 확인할 수 있습니다.
Variational AutoEncoder의 의미
- Variational AutoEncoder(이하 VAE)와 AE는 많이 다르면서도 유사한 구조를 가집니다. VAE는 다소 복잡하므로 먼저 의미 관점에서 살펴보고 자세한 수식적인 내용은 VAE의 의미를 살펴본 뒤 자세하게 다루도록 하겠습니다.
VAE는 랜덤 노이즈로 부터 원하는 영상을 얻을 수 없는 지에 대한 의문에서 시작됩니다.

- 예를 들어 위 그림과 같은 2D 랜덤 노이즈를 입력으로 받았을 때, 어떤 영상(ex. 사람)을 만들어 낼 수 있는 지에 대한 문제입니다.
- 위와 같은 영상에서 랜덤 노이즈를 이용하여 만들 수 있는
영상의 갯수는 \(256^{height X width X 3(\text{RGB})}\) 정도로 생각할 수 있습니다.

- 예를 들면 랜덤 노이즈를 통하여 위 그림과 같은 이미지를 얻을 확률은 \(1 / 256^{height X width X 3(\text{RGB})}\) 라고 생각할 수 있습니다.
- VAE의 처음 질문이 랜덤 노이즈로 부터 원하는 영상을 얻을 수 없을까? 였는데 이와 같은 천문학적인 경우의 수에서 임의로 생성한 데이터로 원하는 영상을 얻을 수는 없습니다.
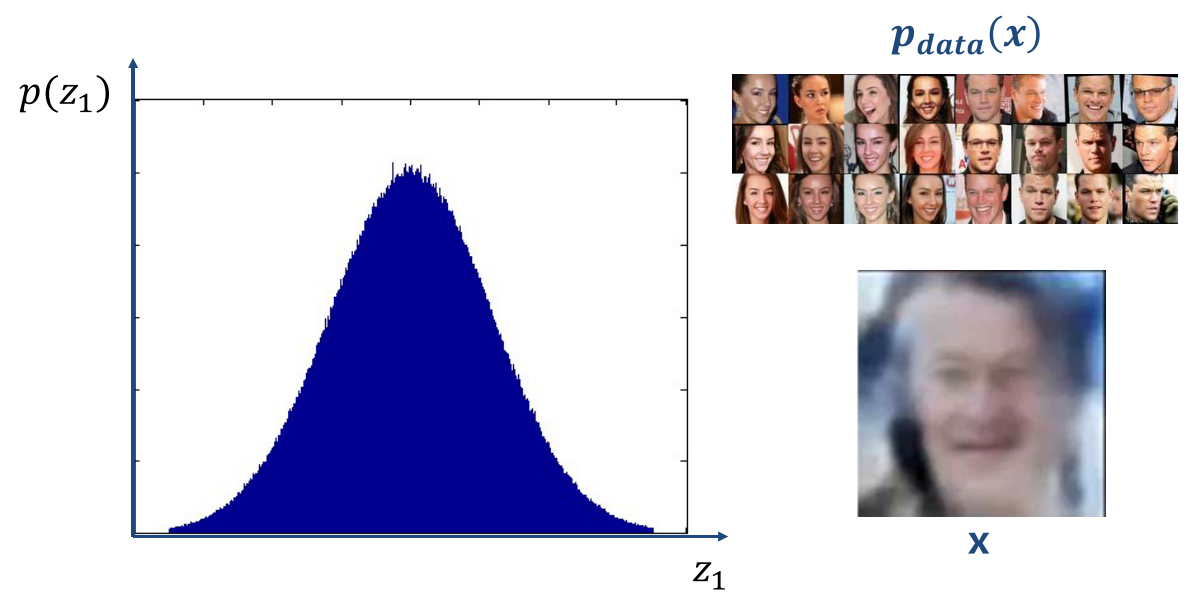
- 만약 \(P_{\text{data}}(x)\) 라는 데이터셋이 있고 이 데이터셋을 이용하여 데이터셋을 잘 나타내는 분포를 만들고 랜덤 노이즈가 그 분포 중 하나에 해당되도록 한다면 데이터셋을 나타내는 분포 내에서 랜덤값이 생성되기 때문에 데이터셋과 유사한 값을 뽑아낼 수 있습니다. 예를 들면 위 그림의 희미한 사진과 같습니다. 참고로 위 분포는 VAE의
latent variable의 분포에 해당합니다. - 이러한 방법은 앞서 예시를 든 Unifrom한 랜덤 노이즈를 만드는 것과 다르게 데이터셋이 가지는 확률 분포 내에서 랜덤 노이즈를 만드는 것으로 차이가 있습니다.
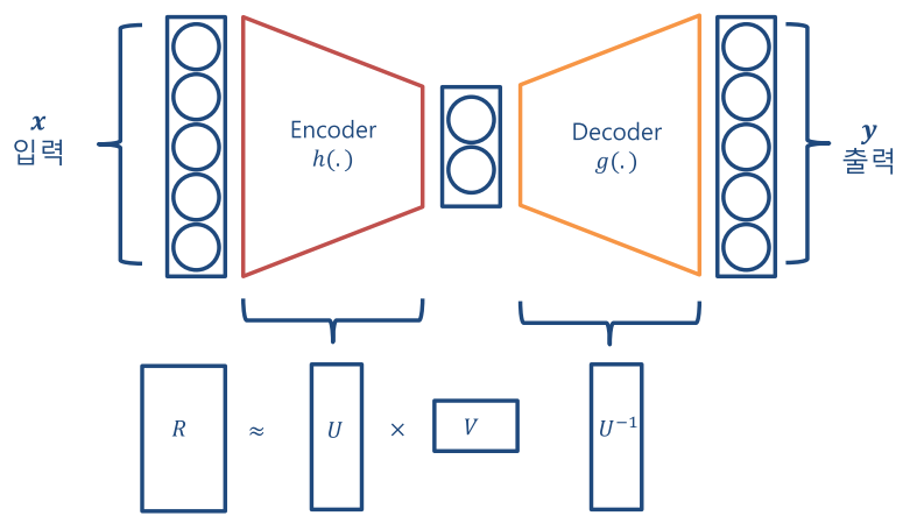
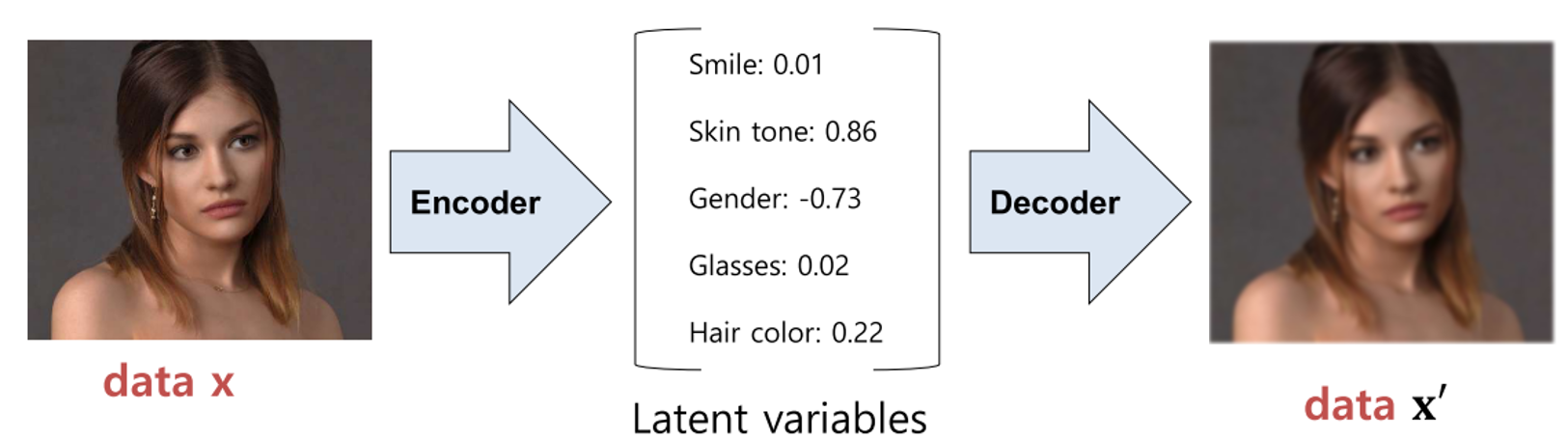
- 이 문제를 다루기 위해서
AE내용에서 부터 시작해 보겠습니다. AE의 주 목적은 차원 축소를 통하여latent variable을 얻는 것에 있습니다. 예를 들면 위 그림에서 latent variable의 값이 특징들을 나타내는 것 처럼 feature extractor의 기능을 가지고 있습니다. (물론 latent variable이 실제 위와 같이 의미 단위로 뽑지는 않고 이해를 돕기 위한 예시 입니다.)- 즉,
AE는 sample을 통해 위 그림과 같은 Encoding, Decoding을 학습을 하고 이는 선형대수학에서 다루는 Nonlinear Matrix Factorization 또는 Nonlinear dimension reduction 컨셉과 일치합니다. - Sample의 차원을 줄였다 늘리는 과정을 통하여 sample을 잘 설명하는
latent variable을 도출하는 네트워크를 학습합니다.
- 반면
VAE의 주 목적은 데이터를 생성하기 위함입니다. 따라서 데이터의 분포 자체를 학습합니다. latent variable 분포로부터 sampling 된latent variable을 decoder의 input으로 활용합니다.
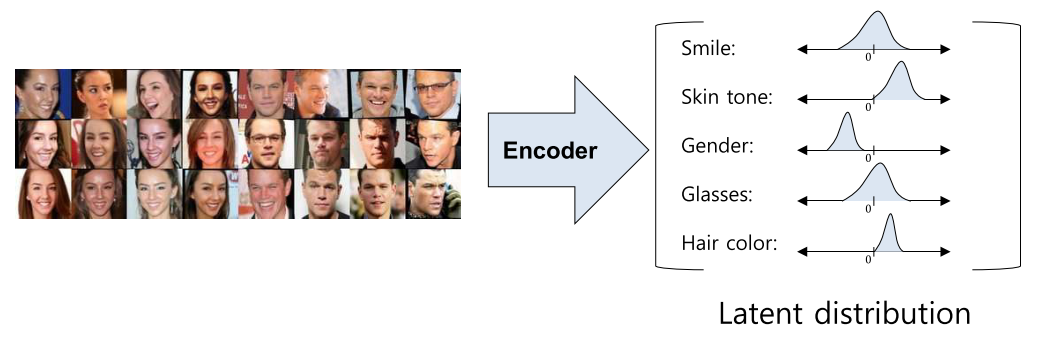
- 데이터셋이 VAE의 Encoder 쪽으로 들어가면 latnet variable의 분포인 latent distribution으로 나타내어 집니다.
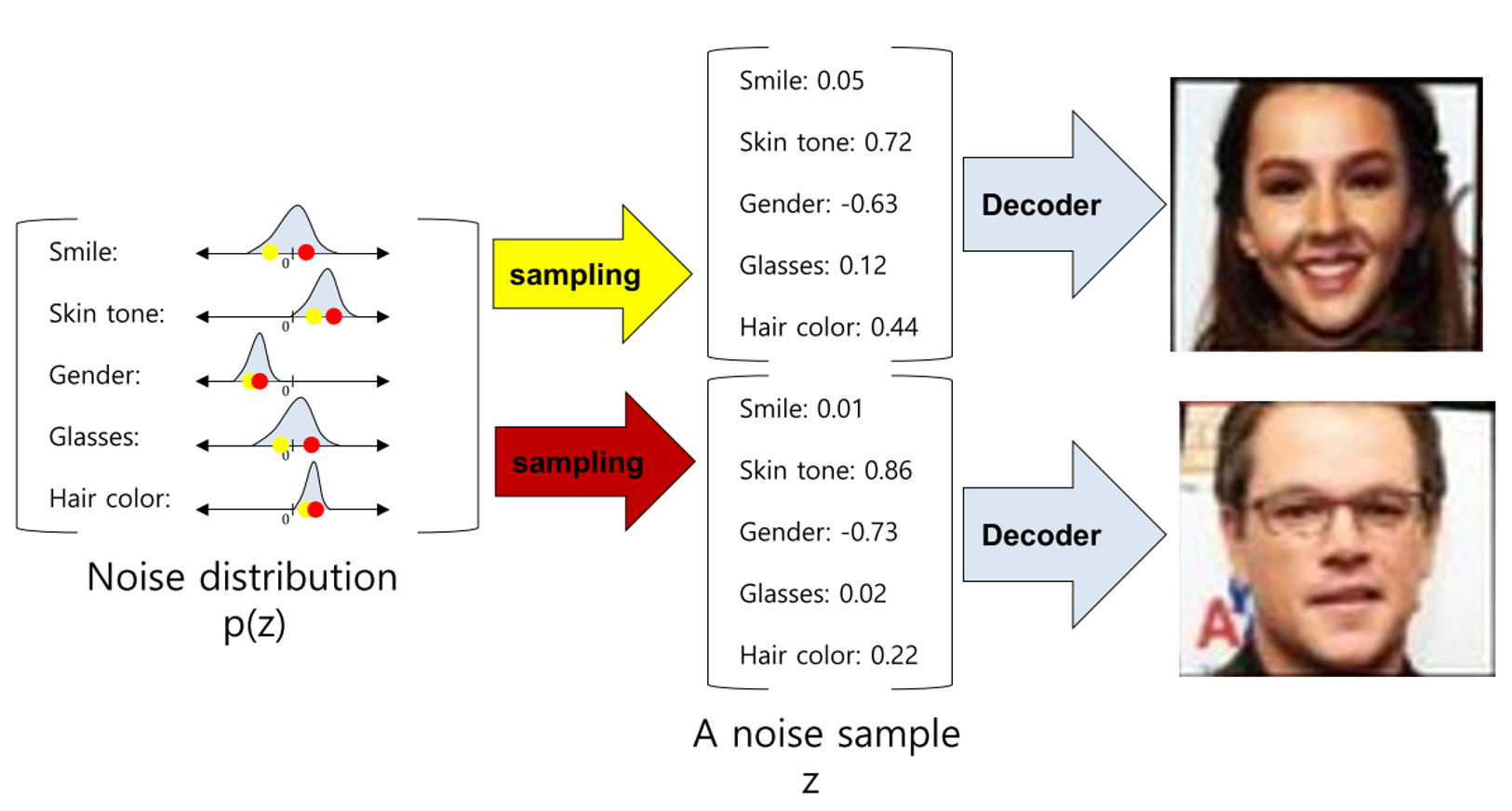
- latent distribution에서 랜덤값으로 샘플링을 하면 latent distribution에 대응 되는 의미에 따라 다른 출력의 이미지를 생성하도록 할 수 있습니다.
- 위 예시에서는 노란색 / 빨간색 샘플링 방식에 따라 전혀 다른 모습의 이미지가 생성된 것을 볼 수 있습니다.
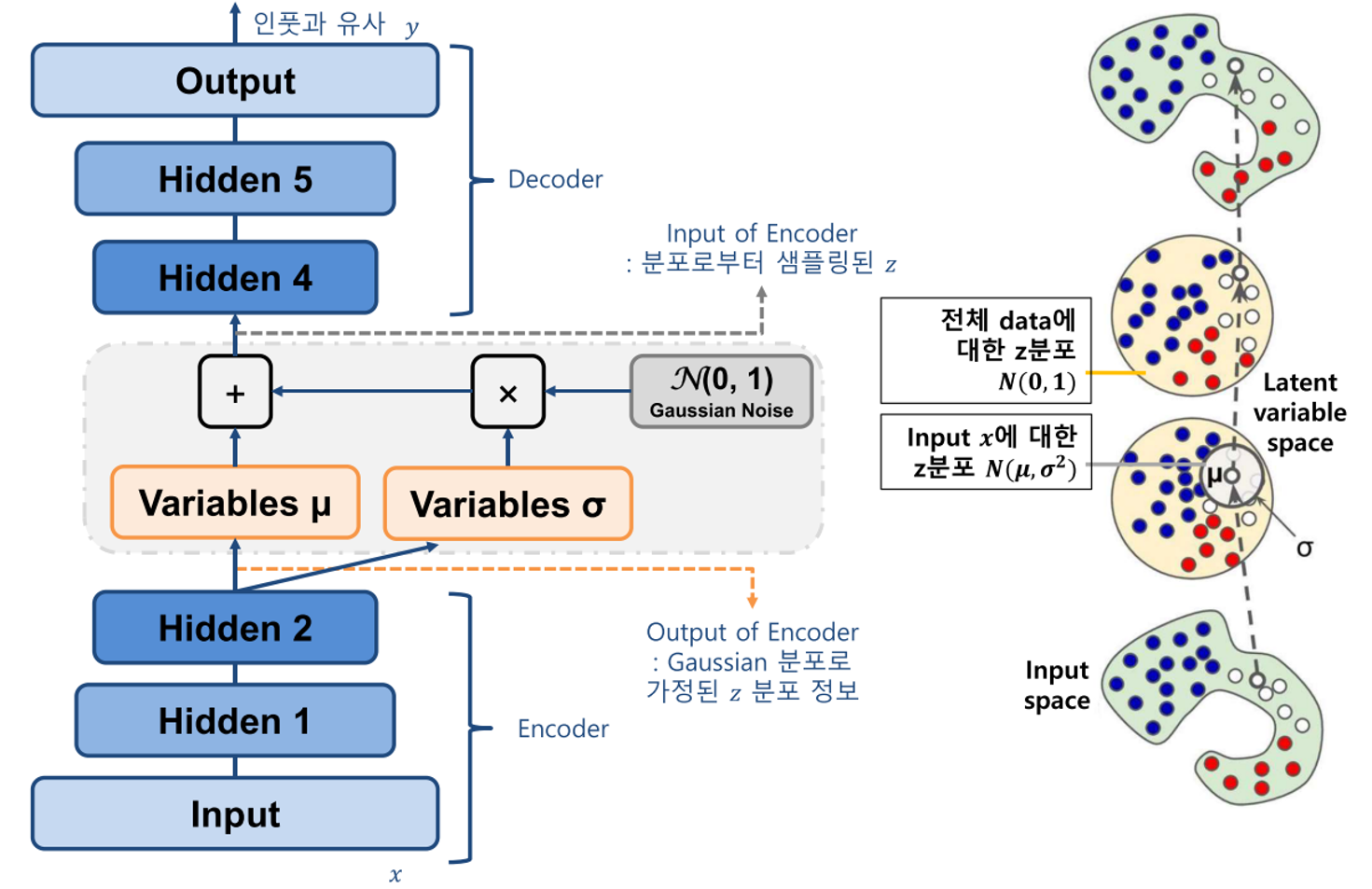
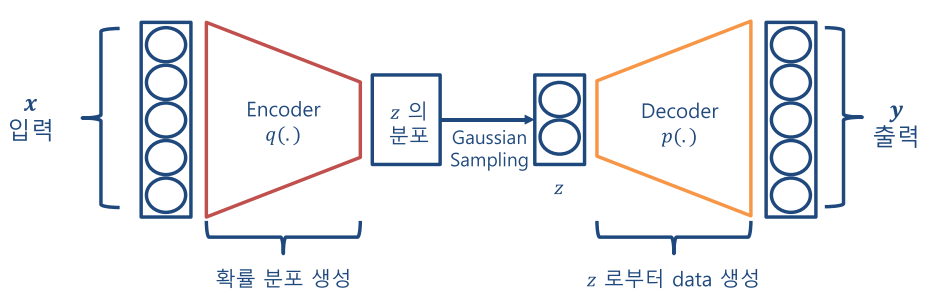
- VAE의 전체 아키텍쳐를 보면 인풋으로 데이터를 받은 뒤 Encoder 부분에서는 latent variable을 생성하도록 학습합니다.
- 이 때, AE와는 다르게 latent variable로 \(\mu, \sigma\)를 생성합니다.
- 가우시안 노이즈 \(N(0, 1)\)과 ① latent variable \(\sigma\)와 곱해지고 ② \(\mu\)와 더해져서 Decoder의 Input으로 전달되어 집니다.
- Decoder에서는 이 값을 원본 데이터 해상도 만큼 복원시켜서 원본 인풋과 유사해지도록 학습합니다.
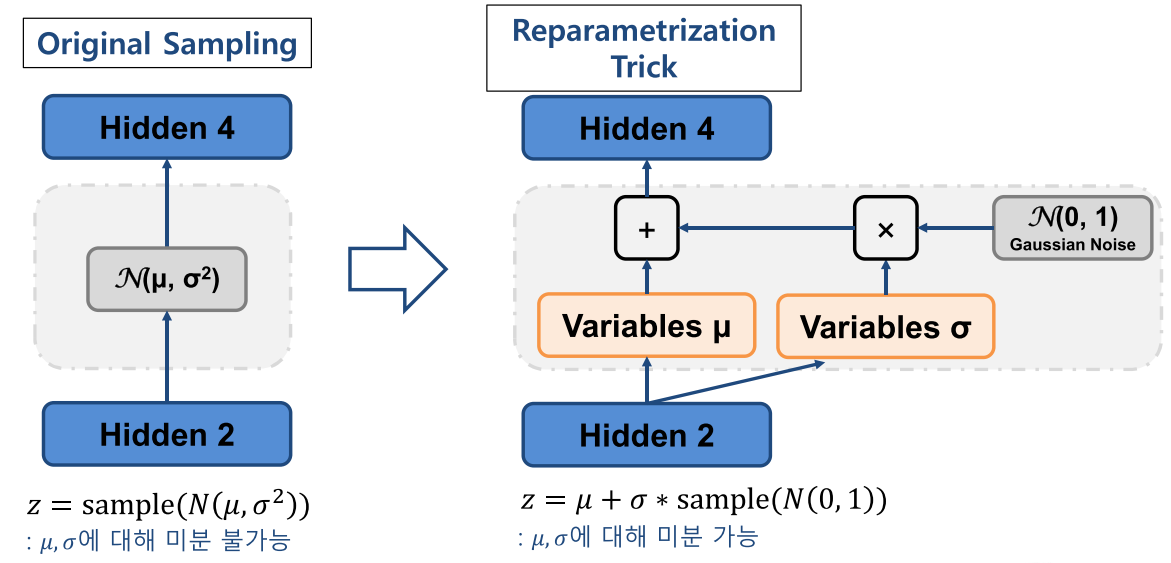
- AE와 VAE의 핵심적인 차이점은 latent variable에 대한 표현 방식입니다. VAE에서는 latent variable의 distribution을 정규 분포 형태로 나타내고 그 분포에서 샘플링을 하도록 합니다.
- 여기서 중요한 점 중의 하나는 VAE 또한 딥러닝 네트워크이기 때문에 backpropagation을 통한 학습이 가능하도록 아키텍쳐를 구성해야 한다는 것입니다.
- 위 그림의 왼쪽을 보면 단순히 정규 분포에서 샘플링 하도록 하면 Encoder와 Decoder 사이의 latent variable에서 미분이 불가능해집니다.
- 반면 오른쪽과 같이 Encoder의 출력부에서 \(\mu, \sigma\)를 출력하도록 하고 이 값의 선형 결합을 통해 가우시안 분포의 샘플링을 하도록 하면 \(\mu, \sigma\)에 대하여 미분이 가능해 집니다. 이러한 방법을
Reparametrization Trick이라고 합니다.
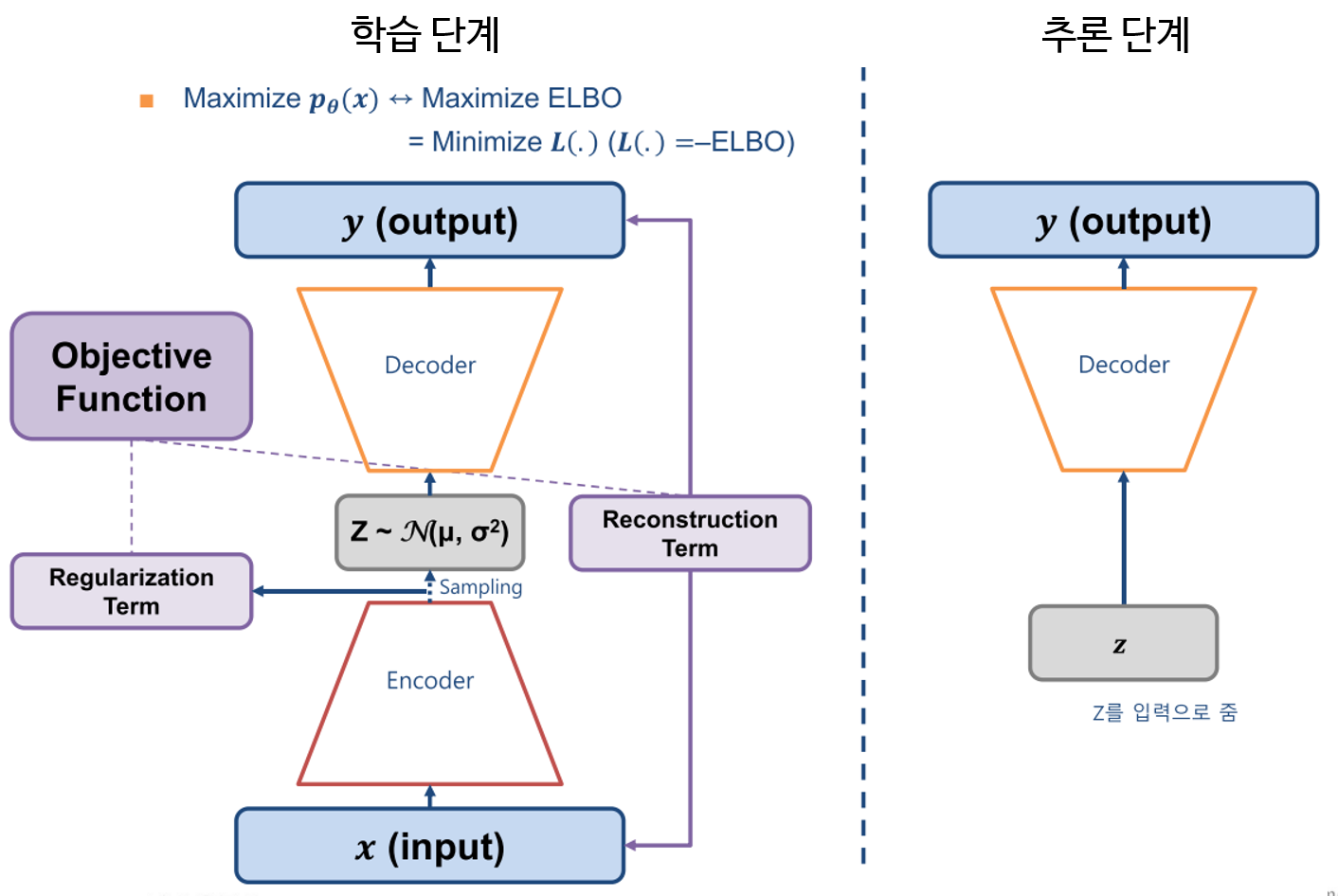
- 앞에서 설명한 것을 종합하면
학습 단계에서의 VAE에서는 위 그림과 같이 Encoder, Decoder 그리고 Latent Variable Distribution을 이용하여 네트워크를 구성하고 네트워크의 입력과 출력이 Reconstruction이 잘 되도록 학습을 합니다. 추론 단계에서는 Encoder 부분을 떼어내고 latent variable에서 샘플링을 한 후 Decoder를 통해 출력을 하면 새로운 이미지를 출력하도록 할 수 있습니다.

- 사람 얼국 데이터셋을 학습하여
VAE를 통해 샘플링 한 결과를 위 그림과 같이 확인할 수 있습니다. 기본적인 VAE를 통해 데이터를 생성하면 위 그림과 같이 약간 blur한 특징을 가집니다. - 이 점은 VAE의 특징이자 단점이며 이 이유에 대해서는 아래 상세 내용을 살펴보면서 다루겠습니다.