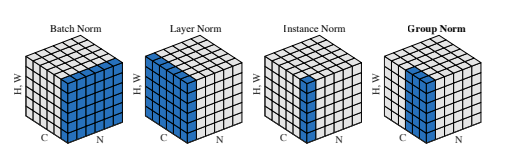
딥러닝에서의 다양한 Normalization 방법
2020, Nov 23
- 참조 : https://mlexplained.com/2018/11/30/an-overview-of-normalization-methods-in-deep-learning/
- 참조 : https://ocw.mit.edu/resources/res-6-007-signals-and-systems-spring-2011/
- 참조 : https://youtu.be/rVBfM0A3oWY
목차
-
Normalization과 Regularization
-
Batch Normalization의 한계
-
Weight Normalization
-
Layer Normalization
-
Instance Normalization
-
Group Normalization
Normalization과 Regularization
- 이 글에서 설명할 Regularization은 정규화 라고 불립니다. 반면 Normalization의 경우에도 정규화라고 불립니다. 따라서 같은 정규화 라는 단어로 사용되기 때문에 종종 헷갈릴 수 있습니다. 따라서 차이점을 정확하게 확인하고 넘어가시길 바랍니다.
Normalization: 데이터에 scale을 조정하는 작업Regularization: predict function에 복잡도를 조정하는 작업
- 예를 들어 데이터가 매우 다른 scale(하한값과 상한값의 범위가 매우 큰 경우)에있는 경우 데이터를
Normalization할 수 있습니다. 이 때, 대표적으로 평균 및 표준 편차와 같은(또는 호환 가능한) 기본 통계를 이용하여 데이터를 변경합니다. 이는 학습된 모델의 정확도를 손상시키지 않으면서 데이터의 Scale을 조정하여 데이터의 분포 범위를 조절할 수 있습니다.
- 모델 학습의 한 가지 목표는 중요한 feature를 식별하고 noise(모델의 최종 목적과 실제로 관련이 없는 random variation)를 무시하는 것입니다. 주어진 데이터에 대한 오류를 최소화하기 위해 모델을 자유롭게 조정하는 경우 과적합이 될 수 있습니다. 모델은 이러한 임의의 변형을 포함하여 데이터 세트를 정확하게 예측해야합니다.
Regularization은 복잡한 함수보다 더 간단한 피팅 함수에 보상(reward)을 합니다. 예를 들어, RMS 에러가 x 인 단순 로그 함수가 오류가 x / 2 인 15 차 다항식보다 낫다고 말할 수 있습니다. 이러한 모델 단순화의 정도와 에러에 대한 트레이드 오프 조정은 모델 개발자에게 달려 있습니다.
Batch Normalization의 한계
- 딥러닝에서 가장 많이 사용되는 Normalization의 방법은
Batch Normalization이며 Batch Normalization을 통해 좋은 성능을 얻어왔기 때문에 현재도 많이 사용중입니다. - 하지만 Batch Normalization에도 한계점이 존재하기 때문에 다른 Normalization 방법들이 제시되고 있습니다.
- 먼저
Batch Normalization의 의미는 다음 링크에서 참조하시기 바랍니다. - 그러면
Batch Normalization의 한계에 대하여 살펴보도록 하겠습니다.
- \[\mu_{\text{batch}} = \frac{1}{B} \sum_{i} x_{i} \tag{1}\]
- \[\sigma^{2}_{\text{batch}} = \frac{1}{B} \sum_{i} (x_{i} - \mu_{\text{batch}})^{2} \tag{2}\]
- 먼저
Batch Normalization은 batch의 크기에 의해 영향을 받는 다는 것이 주요한 단점 입니다. - 예를 들어 극단적으로 Batch가 1이면 식 (1), (2)에 따라 \(\mu = x_{1}, \sigma = 0\) 이 되어버리게 되어 Normalization 시 0으로 나누어 주는 문제가 발생을 하게 되고 이렇게 \(\mu, \sigma\) 를 구하는 것은 통계적으로 의미가 없기 때문에 문제가 발생합니다.
- batch의 크기가 어느 정도 커지면 큰 수의 법칙에 의하여 샘플들이 가우시안 분포를 이루게 될것을 기대하나 batch가 너무 작아버리면 가우시안 분포를 가지지 못하게 됩니다.
RNN학습 시 Backpropagation Through Time을 하면 시간축으려 펼쳐야 하기 때문에 batch의 크기가 커지면 메모리 문제가 발생하기도 합니다. 따라서RNN에서는 batch의 크기를 작게해야 하는데 이 경우 앞에서 언급한 batch normalization 문제가 발생합니다. (큰 CNN도 동일한 이유로 한계가 발생합니다.)- 반대로
batch의 크기를 크게 해도 문제가 발생합니다. batch의 크기가 너무 커지게 되면 다양한 데이터가 많아질 수 있고 multi modal 형태의 분포가 발생할 수도 있습니다. 즉, 가우시안 분포라는 가정에서 벗어날 수 있습니다. - 뿐만 아니라 batch가 너무 커지면 병렬화 연산 효율이 떨어질 수 있고, 학습 시 gradient를 계산해서 반영하는 데 시간이 오래 걸리기도 합니다.