RMSProp

이전 글 : Gradient Descent with Momentum

이전 글에서는 모멘텀이 그래디언트 디센트를 빠르게 할 수 있다는 것에 대하여 배웠습니다.
이번 글에서 배워볼 알고리즘은 RMSProp(Root Mean Square Prop) 입니다.

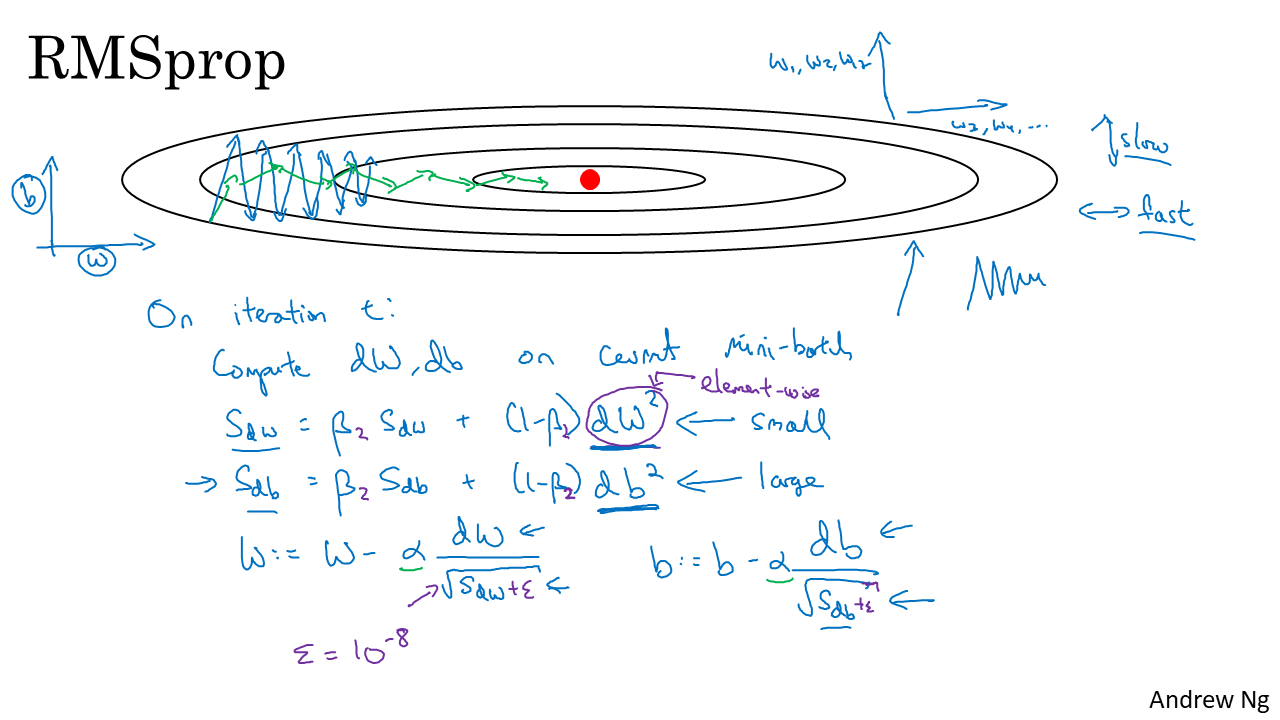
이번 글에서 배울 RMSProp 또한 그래디언트 디센트에서 발생할 수 있는 진동하는 문제를 해결할 수 있는 방법을 배우려고 합니다.
편의상 수직축을 \(b\) 라고 두고 수평축을 \(w\) 라고 두겠습니다.
그렇다면 현재 파란색 선으로 이루어진 그래디언트 디센트에서는 수직축으로의 이동 속도를 늦추고 수평축으로의 이동 속도를 빠르게 한다면 그래디언트 디센트 문제를 개선할 수 있습니다.
RMSProp에서도 먼저 배 iteration 마다 각 배치에 대한 \(dw, db\)를 계산합니다.
그 다음으로 모멘텀과 유사하지만 식이 조금 변형됩니다. \(s_{dw} = \beta * s_{dw} + (1-\beta)*dw^{2}\) 으로 도함수 값을 변형해 줍니다. 이 때 \(dw^{2}\)은 element-wise 연산으로 계산해주면 됩니다.
- 간단히 말하면 도함수의 제곱을 지수 가중 평균 해주는 연산이라고 할 수 있습니다.
위와 동일하게 bias에 대해서도 \(s_{db} = \beta * s_{db} + (1-\beta)db^{2}\) 으로 정의할 수 있습니다.
그 다음으로 \(s_{dw}, s_{db}\)를 weight와 bias를 업데이트 하는 방법이 그래디언트 디센트 또는 모멘텀과 조금 달라집니다.
식을 보면 \(w = w - \alpha * \frac{dw}{\sqrt{s_{dw}}}\) 와 \(b = b - \alpha * \frac{db}{\sqrt{s_{db}}}\)가 됩니다.
- 여기서 집중적으로 살펴볼 항목은 \(\frac{dw}{\sqrt{s_{dw}}}\) 입니다.
- 도함수 값을 \(s_{dw}\)로 나누게 됩니다. 즉 \(s_{dw}\) 값이 크면 w의 변화량이 작고 \(s_{dw}\)가 작으면 w의 변화량이 커집니다.
따라서 위 슬라이드와 같은 상황에서는 수직축(b축)의 변화는 줄이기 위하여 \(s_{db}\)는 커져야 하고 수평축(w축)의 변화는 크게 만들기 위하여 \(s_{dw}\)는 작아져야 합니다.
실제로 그래디언트 디센트 학습 변화를 보면 수직축에서의 변화량이 크기 때문에(기울기가 더 가파른 것을 볼 수 있습니다.) \(s_{db}\)는 상대적으로 큽니다. 반대로 \(s_{dw}\)는 상대적으로 작습니다.
또한 \(s_{dw}, s_{db}\) 식을 보면 도함수 값에 제곱을 함으로 써 상대적으로 큰 값을 가지는 도함수는 도함수 값은 크지만 나눠지는 값도 커지게 되버리고 도함수 값이 작으면 오히려 나누는 값이 작아지게 되는 효과를 가집니다.
다시 그래디언트 디센트에서의 문제를 보면 파란색 선과 같이 진동하는 형태의 학습에서 RMSProp은 초록색 선과 같이 수직 방향의 진동을 억제하여 학습을 빠르게 할 수 있도록 효과를 줍니다.

또한 러닝 레이트 \(\alpha\)와 곱해지는 항이 무한정 커지지 않고 \(\sqrt{s_{dw}}\)에 의해 나눠지기 때문에 러닝 레이트를 조금 크게 잡아도 되는 장점이 있습니다.
즉, 학습 속도를 빠르게 가져갈 수 있습니다.

지금 까지 다룬 식을 보면 이 알고리즘이 왜 Root Mean Square Prop 인 지 알수 있습니다.
도함수를 제곱해서 결국 제곱근을 얻기 때문이지요.
다음 글에서 배워볼 알고리즘은 모멘텀 + RMSProp입니다. 따라서 모멘텀에서 사용한 \(\beta\)는 \(\beta_{1}\)으로 사용할 예정이고 RMSProp에서 사용한 \(\beta\)는 \(\beta_{2}\)로 사용하려고 합니다.
따라서 위 슬라이드에서 \(\beta_{2}\)로 고쳐보겠습니다.
그리고 중요한 점은 \(W, b\)를 업데이트 할 때, 도함수가 0으로 나누어 지지 않도록 구현해야 오류가 발생하지 않습니다.
- 따라서 분모에 아주 작은 값 \(\epsilon\)을 더해주는 것이 중요합니다. 즉, \(\frac{dw}{\sqrt{s_{dw}} + \epsilon}\) 로 만들어 줍니다. 예를 들어 \(\epsilon = 10^{-8}\) 정도 값이면 충분합니다.

정리하면 RMSProp은 모멘텀과 같이 진동을 줄이는 효과도 있고 더 큰 러닝 레이트를 사용하여 학습 속도를 증가시킬 수 있다는 장점이 있습니다.

다음 글 : Adam Optimization Algorithm