Bias Correction of Exponentially Weighted Averages

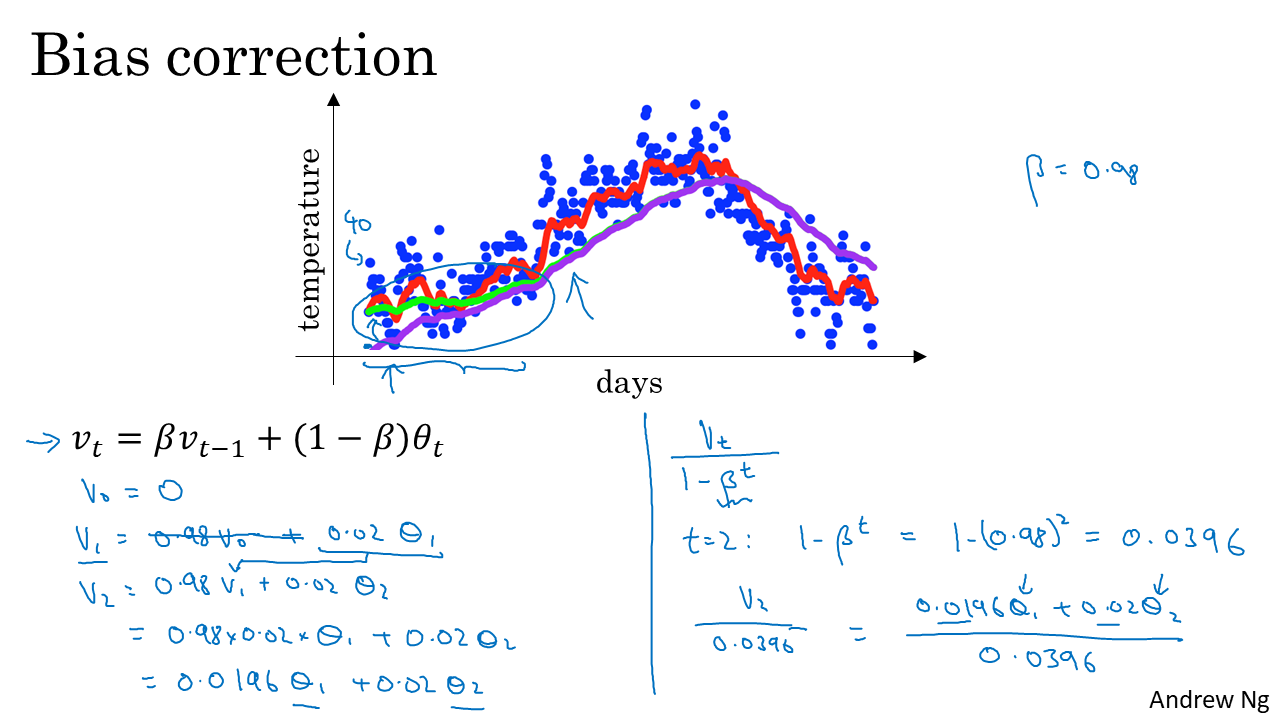
이전 글에서 다룬바와 같이 \(\beta\)가 0.9일 때는 그래프 상에 빨간색 선과 같은 값을 가지고 \(\beta\)가 0.98일 때에는 그래프 상에 초록샌 선과 같은 값을 가지게 됨을 알 수 있었습니다.
하지만 초기값을 어떻게 두느냐에 따라서 보라색 곡선을 가지게 될 수도 있는데, 보라색 곡선의 경우는 처음 값이 실제 데이터의 값을 따라가지 못하고 있는 문제가 있음을 알 수 있습니다.
예를 들어 보라색 곡선의 경우 초기값 \(v_{0}\)을 0으로 두었다고 볼 수 있습니다.
따라서 \(\beta = 0.98\)일 때, 초기값은 \(v_{0} = 0\)이 되고 \(v_{1} = 0.98 * v_{0} + 0.02 * \theta_{1} = 0.02 * \theta_{1}\)이 됩니다.
그리고 \(v_{2} = 0.98 * v_{1} + 0.02 * \theta_{2} = 0.0196 * theta_{1} + 0.02 * \theta_{2}\)가 되는데 이 값 또한 거의 0에 수렴합니다.
이런 초기값을 원래 데이터와 유사하도록 보정해 주는 작업이 필요한데 그 방법이 편향 보정 방법입니다.

위 슬라이드의 오른쪽을 보면 \(v_{t}\) 값에 \(1 - \beta^{t}\) 값을 나누어 줍니다.
예를 들어 t = 2인 경우 \(1 - \beta^{2} = 1 - (0.98)^{2} = 0.0396\)이 되므로 \(\frac{v_{2}}{0.0396} = \frac{0.0196*\theta_{1} + 0.02*\theta_{2}}{0.0396}\)이 됩니다.
- 즉 기존의 값인 \(v_{2}\) 보다 좀 더 값이 커진 상태가 됩니다.
그리고 \(t\)의 값이 점점 커질수록 \(\beta^{t}\)의 값은 0에 수렴하게 되므로 편향 보정을 적용하여도 \(v_{t}\) 와 거의 동일한 값을 가지게 됩니다.
즉, 초기값 부근에서만 값을 보정받을 수 있게 됩니다.
다음 글 : Gradient descent with momentum