
Exponentially Weighted Averages
2019, Jul 17
- 이번 글에서는 그래디언트 디센트 방법보다 빠른 최적화 방법에 대하여 알아 보기 위해서 필요한
지수 가중 평균에 대하여 먼저 학습을 하려고 합니다. - 이후에 학습할 최적화 알고리즘에는 지수 가중 평균 개념을 이용하게 됩니다. 그러면 지수 가중 평균의 개념에 대하여 알아보도록 하겠습니다.
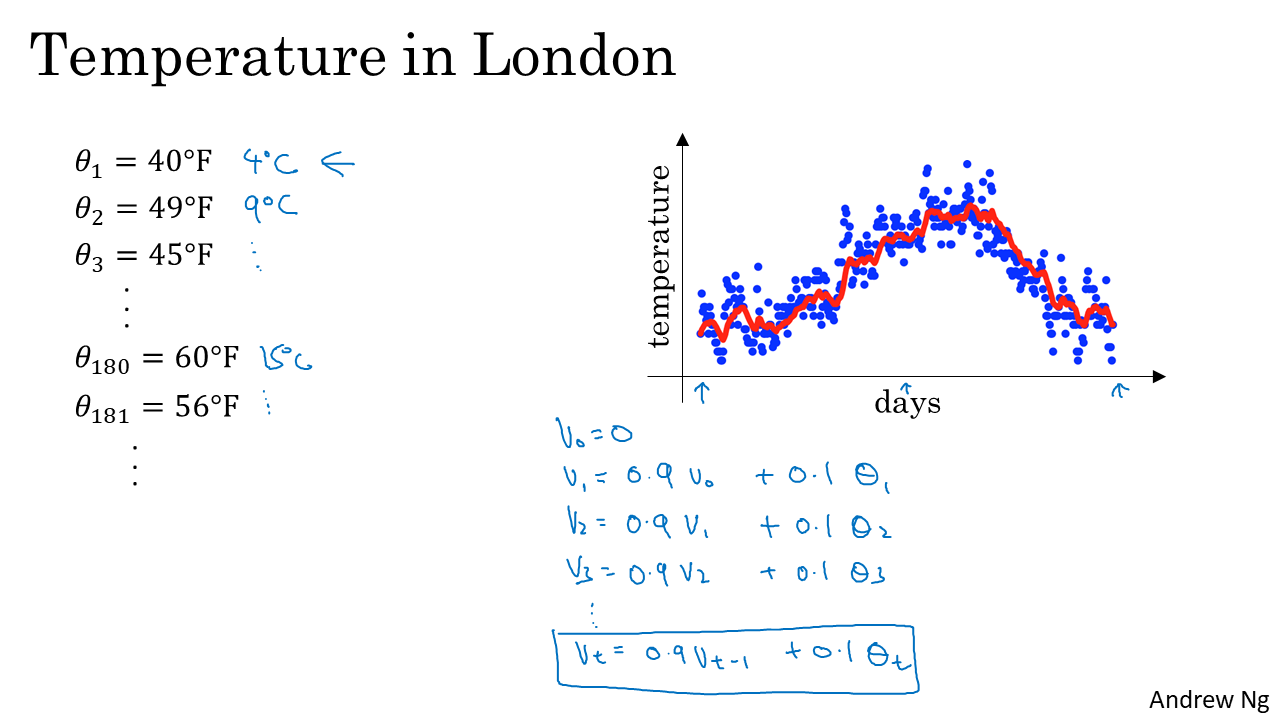
- 위 슬라이드의 데이터는 런던의 기온에 관련된 시간대 별 자료입니다.
- 데이터의 전체 흐름을 보면 경향이 보이긴 하지만 노이즈 같은 데이터 들도 종종 보입니다.
- 저희는 이런 노이즈 데이터 들을 없애면서 전체 경향을 확인할 수 있는 평균 값을 구하고 싶은데 이 때 사용할 수 있는 방법이
지수 가중 평균입니다. - 예를 들어 초기값을 \(v_{0} = 0\) 으로 설정하고 그 다음 날짜의 값은 이전 날짜의 온도 값에 0.9를 곱한 값과 오늘 날짜 온도에 0.1을 곱한 값을 더해줍니다.
- 즉, \(v_{1} = 0.9 * v_{0} + 0.1 * \theta_{1}\) 이 됩니다. (\(\theta_{1}\) 은 1일의 온도 입니다.)
- 그러면 둘째 날의 온도는 \(v_{2} = 0.9 * v_{1} + 0.1 * \theta_{2}\) 가됩니다. 이와 같은 방법을 이용하면 \(t\) 일에는 \(v_{t} = 0.9 * v_{t-1} + 0.1 * \theta_{t}\)로 일반화 할 수 있습니다.
- 이 때, \(v_{i}\)의 값들을 그래프로 나타내면 위 슬라이드의 빨간색 곡선처럼 나타낼 수 있습니다. 이 값이
지수 가중 평균에 해당합니다.
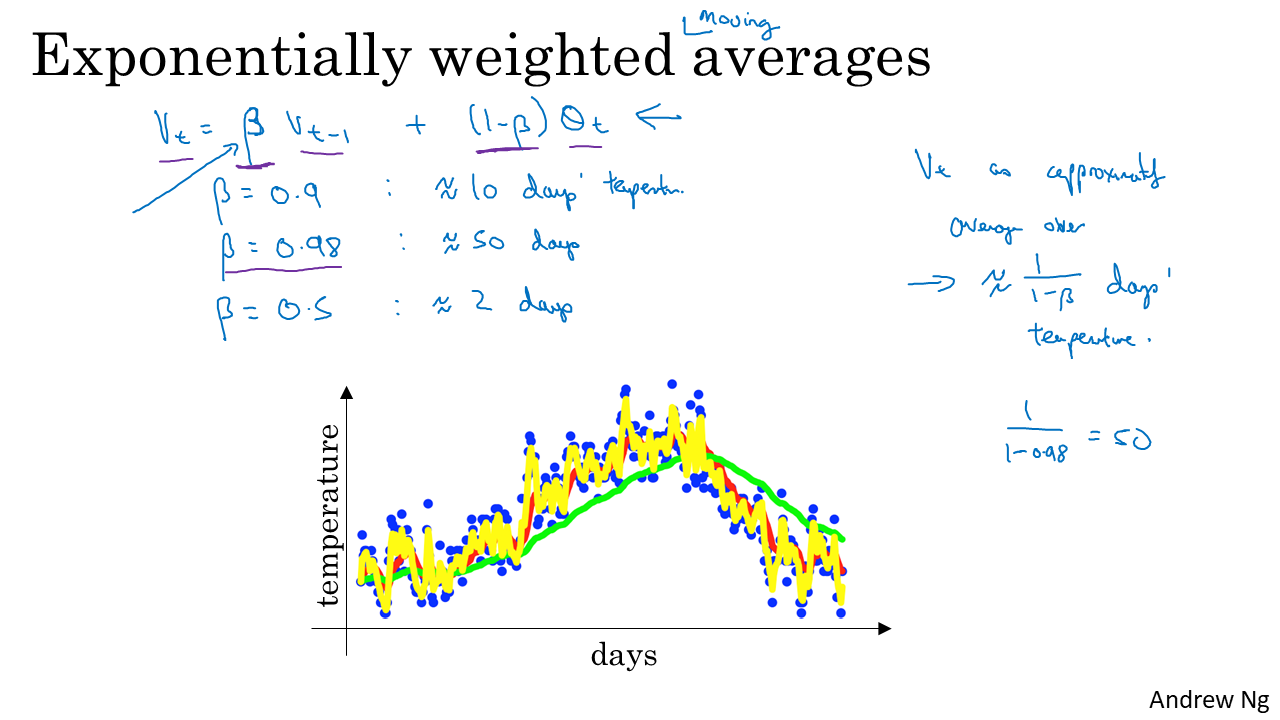
- 그러면 앞에서 구한 식의 의미를 좀 더 자세하게 알아보도록 하겠습니다.
- 앞에서 사용한 상수를 \(\beta\) 라고 사용하면 \(v_{t} = \beta * v_{t-1} + (1-\beta)*\theta_{t}\) 가 됩니다.
- 나중에 살펴보겠지만, \(v_{t}\) 값은 대략적으로 \(\frac{1}{(1-\beta)} * \theta_{t}\)와 같습니다.
- 예를 들면 \(\beta\)가 0.9 이면 이는 10일 동안 기온의 평균과 유사합니다. (위 슬라이드의 빨간색 선입니다.)
- 만약 \(\beta = 0.98\) 이면 50일 동안 기온의 평균과 유사해 집니다. 여기서 눈여겨 볼 것은 \(\beta\)가 1에 가까워지면 더 오랜 시간 동안의 평균값을 참조한다는 것입니다.
- 위 슬라이드의 초록색 선에 해당합니다.
- 그래프를 보면 알 수 있듯이 \(\beta\) 값이 1에 점점더 가까워 질수록(커질수록) 선이 더 부드러워 집니다. 왜냐하면 더 많은 날짜의 기온의 평균을 이용하기 때문입니다.
- 반면 \(\beta\) 값이 더 커질수록 곡선이 올바른 값에서 점점 더 멀어집니다. 왜냐하면 더 오래된 범위 까지 보기 때문에 더 큰 범위에서 기온을 평균하기 때문입니다.
- 따라서 \(\beta\) 값이 클수록 기온이 바뀔 경우에 지수 가중 평균은 더 느리게 반응합니다. 따라서 값이 지연되는 시간(latency)이 큽니다.
- 만약 \(\beta = 0.5\) 라면 2일 동안의 평균값과 유사합니다. 즉, 앞에서 살펴본 케이스에 비하여 평균값에 가중치를 덜 주게 됩니다.
- 이 경우 슬라이드의 노란색과 같이 값을 구할 수 있습니다. \(\beta\) 값을 줄인 만큼 현재 입력되는 \(\theta\) 값에 더 민감해 지게 되었고 값의 변화에 좀 더 민감하게 반응할 수 있습니다.
- 입력되는 값 \(\theta\)에 좀 더 민감해진 만큼 노이즈에 좀 더 민감하게 반응하게 되는 단점도 발생합니다.
- 이후에 다를 좀 더 효율적인 그래디언트 디센트에서 변경해야 할 파라미터 중 하나가 \(\beta\) 값입니다.
- 위 슬라이드의 그래프를 보면 빨간색 곡선이 데이터를 가장 잘 표현한 것 처럼 보입니다. 물론 처음부터 빨간색 곡선을 찾기는 어렵습니다.
- 그래디언트 디센트에 지수 가중평균을 접목할 때에도 하이퍼파라미터인 \(\beta\)를 잘 변경하여 가장 좋아 보이는 값을 찾는게 저희가 해야할 일입니다.
- 다음 글에서는 \(\beta\) 값에 대한 좀 더 직관적인 해석을 해보도록 하겠습니다.