Learning Rate Decay

먼저 왜 러닝 레이트를 감소해야 하는 지에 대한 이해를 돕기 위해 위 슬라이드 예제를 한번 보도록 하겠습니다.
먼저 미니 배치를 이용한 학습에서 미니 배치의 크기가 작다면 미니 배치간 데이터의 분포가 상당히 다를 수 있어서 학습 시 일정하게 비용이 줄어들지 않을 수 있습니다.
따라서 파란색 선과 같이 이터레이션을 거듭할수록 최솟값으로 향하긴 하지만 약간의 노이즈가 있는 것처럼 움직이고 정확하게 수렴하지도 않고 주변을 돌아다니게 됩니다.
왜냐하면 어떤 고정된 러닝 레이트 \(\alpha\) 값을 사용했고 서로 다른 미니배치에 노이즈가 있기 때문입니다.
반면에 점점 더 크기가 작아지는 러닝 레이트를 사용하는 경우 초록샌 선과 같이 학습이 될 수 있습니다.
학습 초기에는 빠른 속도로 최솟값으로 줄어들게 되고 이터레이션이 지속되면 러닝 레이트가 줄어들어 값 업데이트 양이 줄어들게 되어 최솟값 주변에 수렴하게 됩니다.

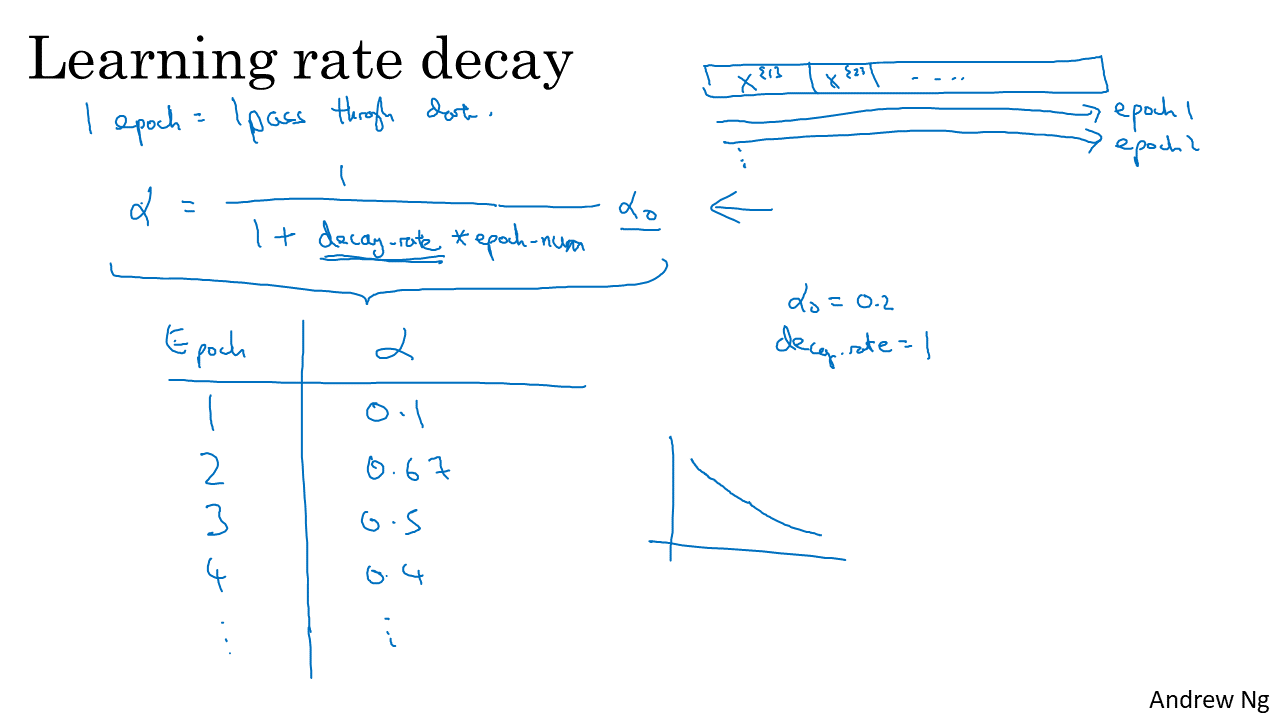
그러면 어떻게 러닝 레이트를 감소하면 좋을까요?
일반적인 방법으로는 1 epoch 마다 모든 데이터를 한번씩 다 학습하게 되므로 epoch 단위로 점점 줄여주는 방법을 사용합니다.
이 때, epoch이 진행될수록 러닝 레이트가 점점 줄어들도록 하면 되는데 예를 들면 위 슬라이드와 같이 줄일 수 있습니다.
위 슬라이드를 보면, \(\alpha = \alpha_{0} / (1 + decay \ rate \ * \ epoch \ num)\) 식으로 업데이트를 합니다.
- 여기서 하이퍼파라미터는 초깃값 \(\alpha_{0}\)와 decay rate입니다.

러닝 레이트를 줄이는 방법에는 다양한 방법이 시도되고 있고 실질적으로도 많은 방법들을 사용하고 있습니다.
예를 들어 지수적으로 감소하는 방법을 사용하면 \(\alpha = 0.95^{epoch} * \alpha_{0}\)와 같이 사용할 수 있습니다.
또는 \(k / (\sqrt{epoch}) , k / (\sqrt{t})\) 등을 곱해줘서 러닝 레이트를 줄여줄 수도 있습니다. (\(k\)는 상수, \(t\)는 배치 크기)
또는 구간을 정해서 이산적으로 러닝 레이트가 줄어들게 할 수도 있습니다.
다음 글 : The problem of local optima