The problem of local optima

이번 글에서는 머신 러닝, 딥 러닝에서 유명한 문제 중 하나인 local optima 문제에 대하여 간략하게 알아보도록 하겠습니다.
학습할 때, 최적화 알고리즘이 좋지 않은 로컬 옵티마 값에 걸리는 것에 대한 걱정이 많았습니다. 최근에는 이론적으로 로컬 옵티마에 대한 극복 방안들이 개선되가는 상태입니다.

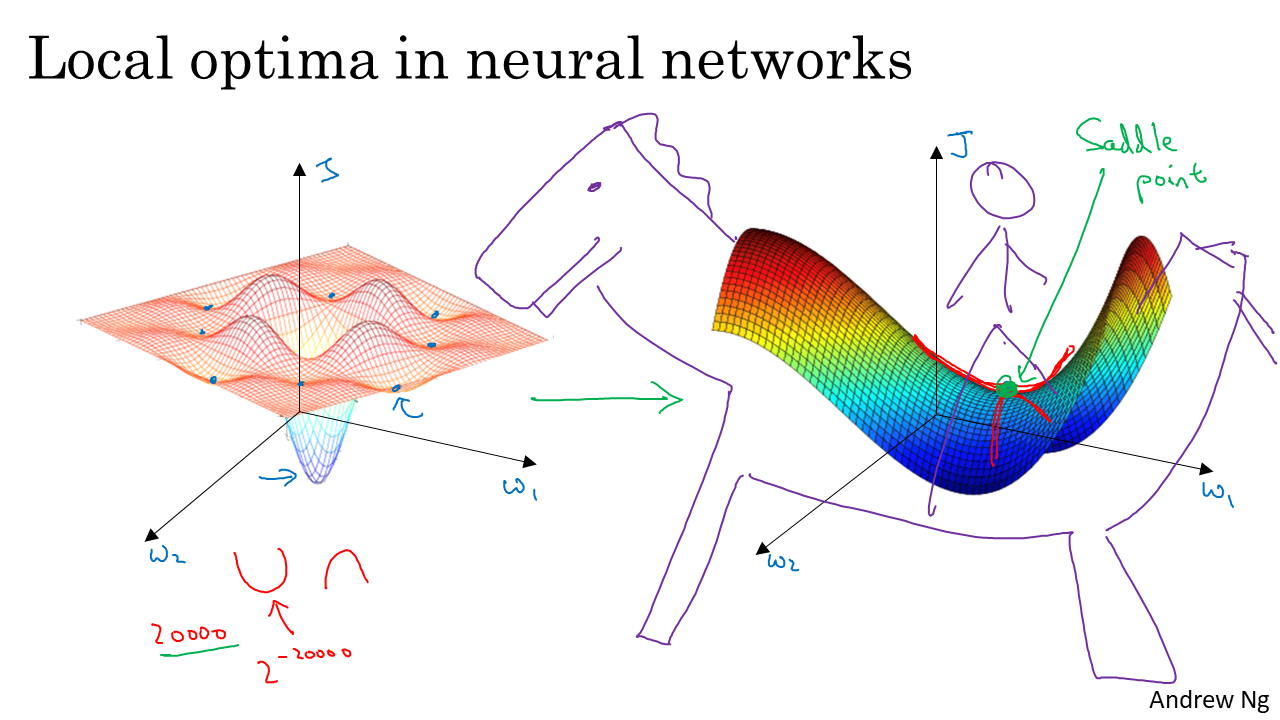
위 슬라이드의 왼쪽 그림이 일반적으로 생각하는 로컬 옵티마의 사례입니다. \(w_{1}, w_{2}\) 평면 축을 가지고 cost라는 세로 축을 가지는 그래프를 보면 중간 중간에 움푹 파인 부분이 로컬 옵티마가 됩니다.
그리고 파란색의 밑으로 푹 파져 있는 부분이 글로벌 옵티마가 되는데 이 지점이 학습의 최종 목적지가 됩니다.
2차원에서는 로컬 옵티마란 것이 다소 간단해 보이지만 신경망과 같은 고차원에서는 로컬 옵티마가 단순한 문제는 아닙니다.
슬라이드 오른쪽을 보면 3차원에서의 로컬 옵티마를 볼 수 있습니다. Saddle Point 라고 표현이 되어 있는 곳은 관점에 따라서 최솟값이 되어 기울기가 0이 되어 버리는 지점이 될 수 있습니다.
Saddle Point가 대표적인 로컬 옵티마의 예가 될 수 있습니다. 말 안장처럼 생겨서 Saddle Point 라고 하며 차원의 기준에 따라서 최솟값이 되기도 하고 최댓값이 되기도 합니다.

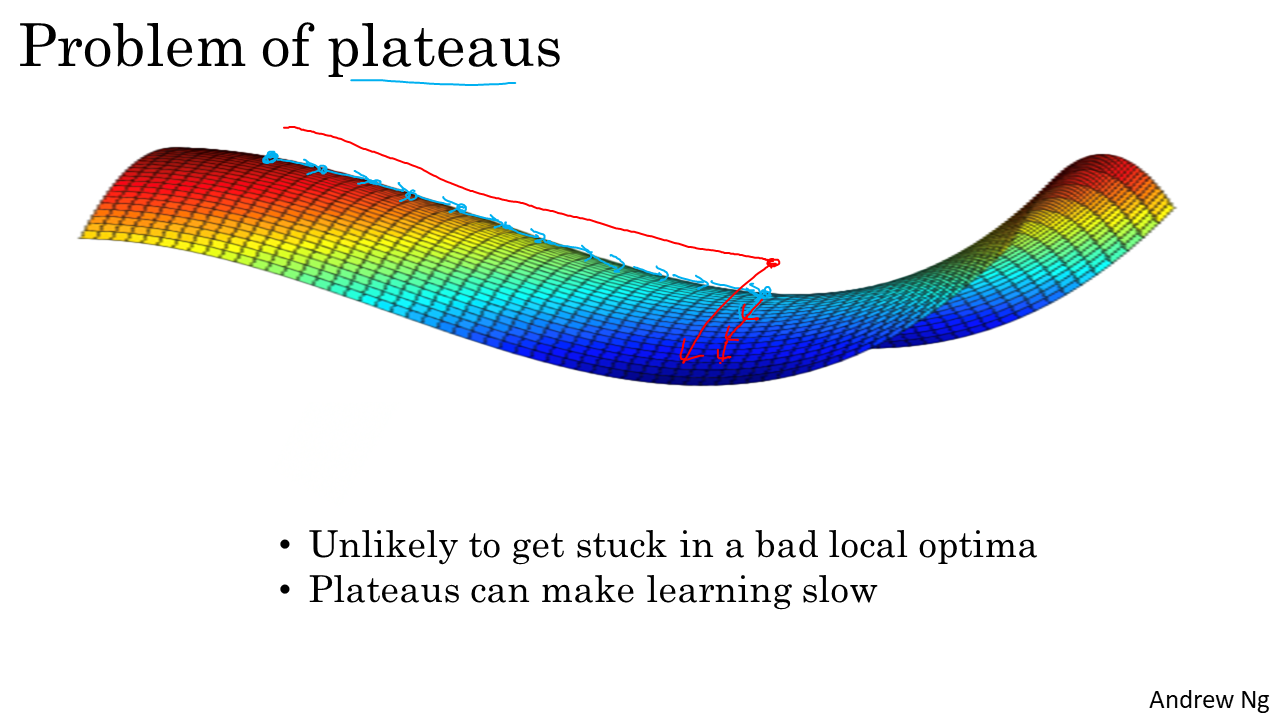
또 다른 대표적인 문제점의 하나는 plateaus 문제입니다. plateaus는 러닝 속도를 저하하는 문제를 일으키는데요.
plateau는 함수 기울기의 값이 0에 근접한 긴 범위를 말합니다. 이 경우에는 도함수 값이 작아서 새로운 차원으로 학습을 하지 않으면 weight의 변화량이 거의 없게 됩니다.

정리를 하면 local optima와 plateau 문제가 대표적인 딥러닝 학습에서의 마주할 수 있는 문제입니다.
하지만 요즘과 같이 고차원의 신경망 학습에서는 local optima에 빠질 가능성이 줄어듭니다. 다양한 차원의 방향으로 최솟값을 찾아나가기 때문입니다.
그리고 plateau문제는 모멘텀 또는 RMSProp, Adam과 같은 최적화 알고리즘이 학습 속도에 가속도를 붙여서 문제 해결에 도움을 줍니다.