Understanding Exponentially Weighted Averages

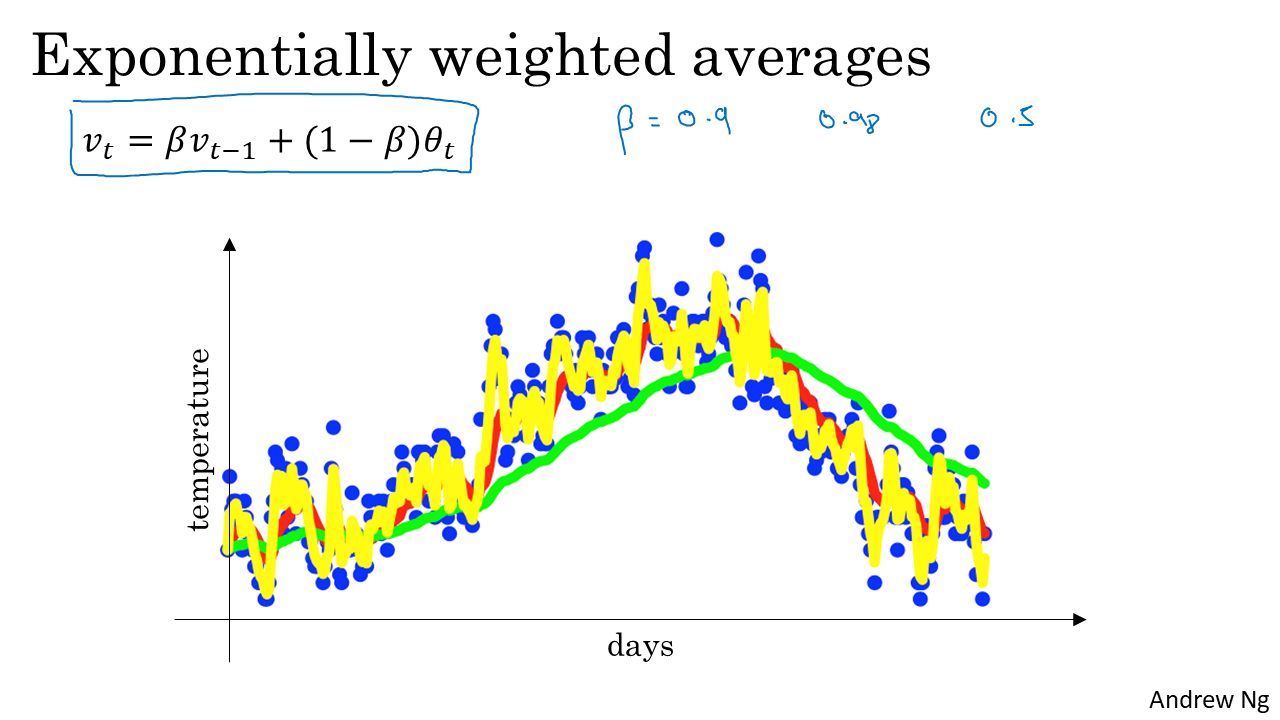
이전 글에서 다룬 바와 같이 \(\beta\) 값에 따라서 지수 가중 평균값이 달라지게 되는데, 0.9일 때에는 빨간색, 0.98일 때에는 초록색, 0.5일 때에는 노란색으로 값을 가지게 됨을 보았습니다.
이 때 가장 적합하게(노이즈를 제거하면서 변화에 잘 적응하는 값) 값을 추적한 것은 \(\beta\) 값이 0.9일 때 였음을 알 수 있었습니다.

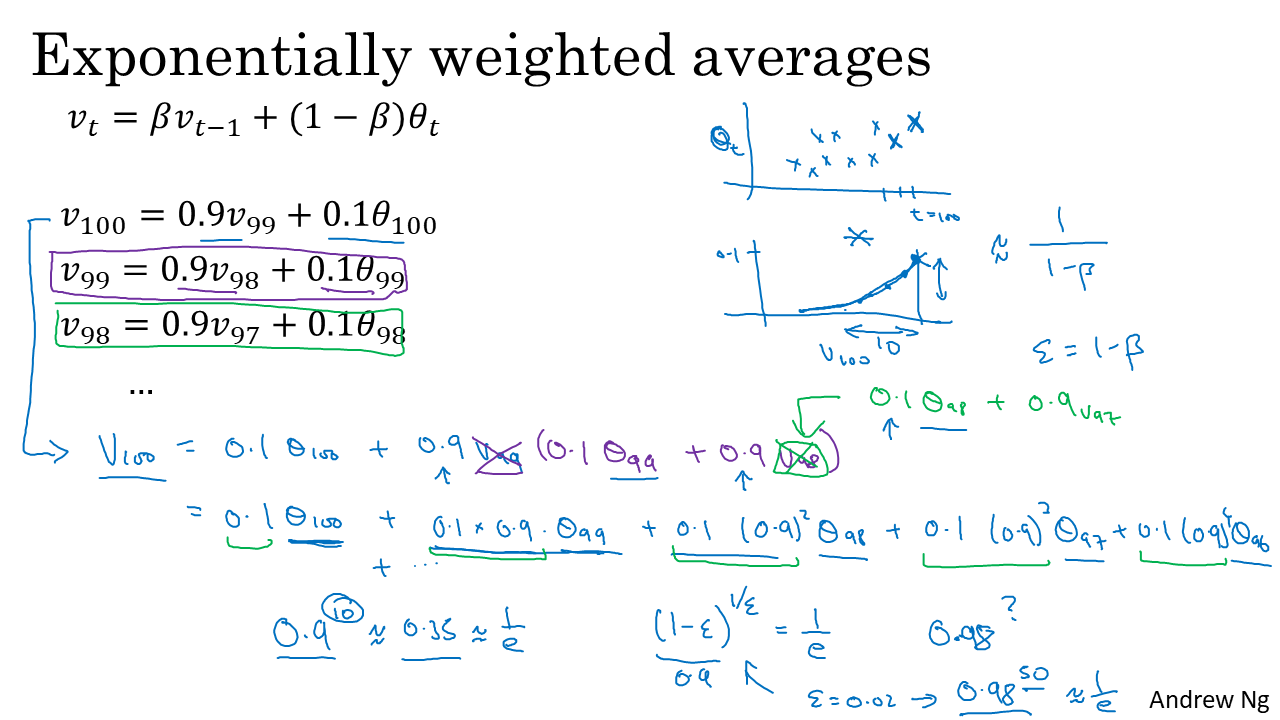
지수 가중 평균은 현재 상태와 이전 상태의 관계로 이루어져 있습니다. 따라서 점화식 형태로 현재 상태와 이전 상태의 관계를 나타낼 수 있었습니다.
점화식 형태로 되어 있으므로 현재(\(t\))상태와 \(t-1\) 상태와의 관계, \(t-2\) 상태와의 관계, 심지어 초깃값과의 관계 또한 정립해 나아갈 수 있습니다.
예를 들어 \(v_{100} = 0.1 * \theta_{100} + 0.9 * v_{99}\) 로 t = 100일 때의 관계를 정할 수 있습니다.
이 때, \(v_{99} = 0.1 * \theta_{99} + 0.9 * v_{98}\) 이므로 식을 정리하면 \(v_{100} = 0.1 * \theta_{100} + 0.9 * (0.1 * \theta_{99} + 0.9 * v_{98})\) 이 됩니다.
- 현재 정리된 식의 \(v_{98}\) 또한 더 이전 상태의 형태로 표현이 됩니다.
따라서 위의 슬라이드와 같이 최종 정리된 형태를 보면 \(v_{100} = 0.1 * \theta_{100} + 0.1 * 0.9 * \theta_{99} + 0.1 * 0.9 ^{2} * \theta_{98} + \cdots\) 이 됩니다.
정리한 식에서 \(\theta\) 앞에 곱해진 계수들을 모두 더하면(등비 급수의 합)1 또는 1과 유사한 값이 됩니다.(\(0.1 + 0.1*0.9 + 0.1 * 0.9^{2} + ...\))
- 이 내용은 다음 글의 편향 보정이라는 내용으로 다루어 보려고 합니다. 결과적으로는 이것에 의해 지수 가중 평균이 됩니다.

이전 글에서 설명한 \(\beta\) 값에 따라 얼마나 많은 이전 상태들이 지수 가중 평균에 영향을 끼치는지 알아보겠습니다.
예를 들어 \(0.9^{10} \approx 0.35 \approx \frac{1}{e}\) 의 관계가 성립합니다.
만약 0.9를 \((1 - 0.1)\)로 표시하고 일반화를 위해 \((1 - \epsilon)\) 로 표현한다면 \(\epsilon\)은 0.1이 됩니다.
이 때, \((1 - \epsilon)^{1/\epsilon} \approx \frac{1}{e}\) 이고 \(\epsilon\) 값이 0에 가까워 질수록 값은 가까워지는 관계를 가집니다.
- 왜냐하면 \(lim_{x \to \inf} (1 + \frac{1}{x})^{x} = e\) 식을 이용하여 변형해 보면 값이 근사해짐을 알 수 있습니다.
아무튼 여기서 중요한 식은 \((1 - \epsilon)^{1/\epsilon} \approx \frac{1}{e} \approx 0.36\) 이고 좌변의 승수에 해당하는 \(1/\epsilon\)의 만큼 곱해져야 약 0.36 정도로 감소되는 것을 알 수 있습니다.
- 즉 \(1/\epsilon\) 일 만큼 걸려야 전체 값의 약 1/3 로 줄어드는 것을 알 수 있습니다. 너무 값이 많이 줄어든 것은 지수 가중 평균에 영향이 적습니다.
따라서 1/3 정도로 값이 줄어든 일수만 대략적으로 살펴보면 \(\frac{1}{\epsilon}\)일 임을 알 수 있습니다.

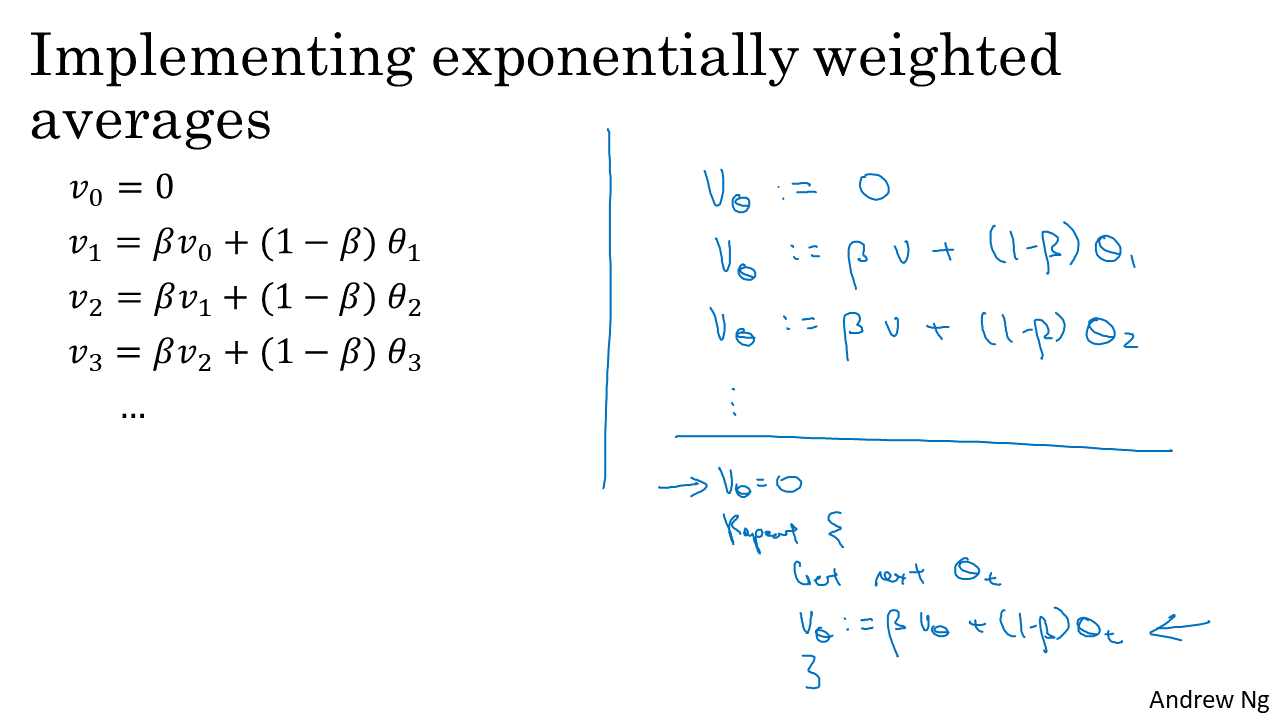
마지막으로 지수 가중 평균을 어떻게 구현하는지에 대하여 알아보도록 하겠습니다.
실질적으로 구현할 때에는 가장 마지막의 \(v_{t}\) 값만 저장하면 됩니다. 매번 케이스 마다 \(\theta\) 값이 들어오면 가장 최근의 갱신된 \(v_{t}\)와 \(\theta\) 를 이용하여 지수 가중평균을 계산하면됩니다.
즉, 실질적으로 저장해야 하는 값은 \(v_{t}\) 값 1개 입니다. 따라서 메모리에 전혀 부담이 없습니다.
다음 글에서는 편향 보정이라는 내용에 대하여 다루어볼 예정입니다. 이 내용 까지 다루면 지수 가중 평균 개념과 그래디언트 디센트 개념을 결합하는 데 문제가 없을것 같습니다.