Understanding mini-batch gradient descent

이전 글 : Mini-batch gradient descent

이번 글에서는 미니 배치 그레디언트 디센트에 관하여 좀 더 자세하게 알아보도록 하겠습니다.
다루어볼 내용으로 그레디언트 디센트를 도입하는 방법과 미니 배치의 역할 그리고 미니 배치가 왜 잘 잘동하는지에 대한 원리에 대하여 알아보도록 하겠습니다.

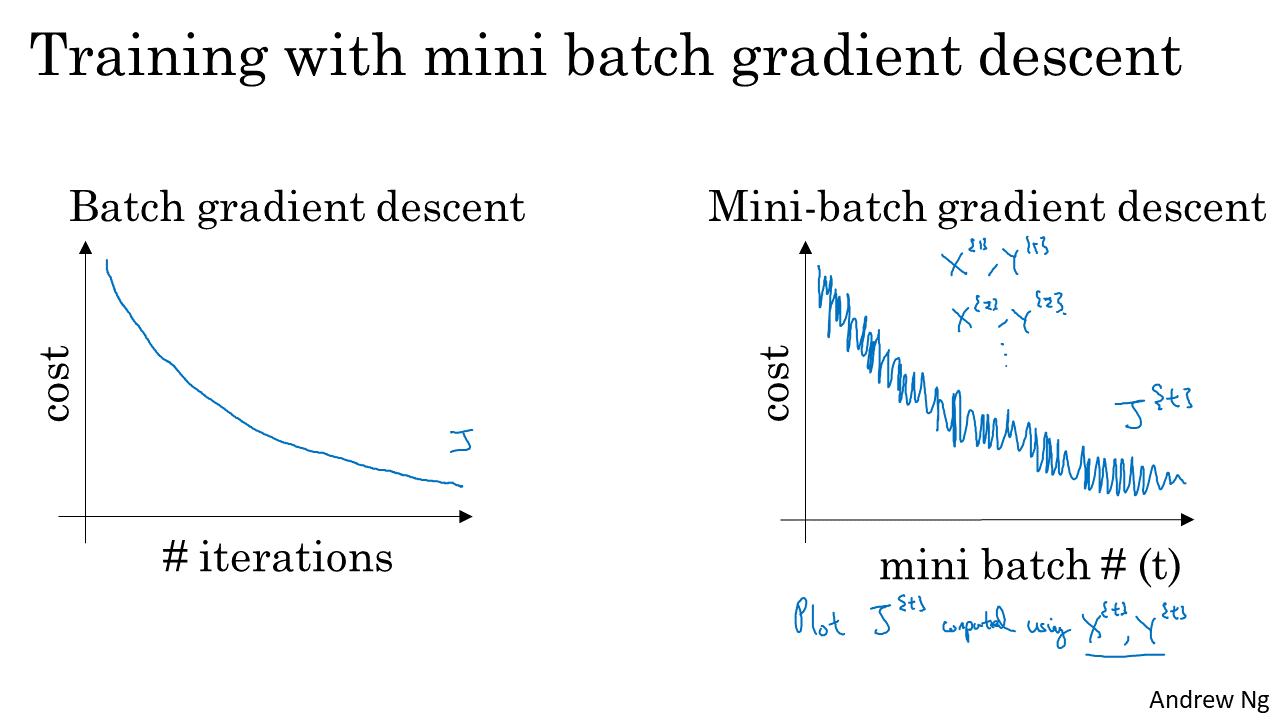
전체 데이터를 다루는 배치 그레디언트 디센트 에서는 왼쪽 그래프와 같이 iteration이 반복될 수록 cost가 감소하는 것을 볼 수 있습니다.
특히 cost가 지속적으로 낮아지는 것을 볼 수 있습니다. 즉, cost 측면에서는 점진적으로 계속 개선되는 것을 알 수 있습니다.
- 일반적인 상황의 배치 그래디언트 디센트에서는 cost가 지속 감소하게 되고, cost가 상승하게 된다면 learning rate가 너무 큰 경우가 아닌 지 생각해볼 수 있습니다.
반면 오른쪽의 미니 배치 그레디언트 디센트 그래프를 보면 cost의 등락이 계속 보이는 형태를 띄면서 전체적으로는 cost가 감소하는 것을 볼 수 있습니다.
미니 배치 그레디언트 디센트에서 이렇게 노이즈가 낀 형태 처럼 cost가 감소하는 이유는 학습 대상이 \(X, Y\) 전체가 아니라 \(X^{(t)}, Y^{(t)}\) 이기 때문입니다.
- 배치 그레디언트 디센트에서는 매번 같은 데이터를 사용하므로 계속 cost가 감소하지만 미니 배치에서는 이터레이션 마다 다른 데이터를 사용하므로 항상 cost가 감소할 수는 없습니다.
- 그리고 미니 배치 단위 별로 데이터의 난이도가 종종 다를 수가 있어서 cost가 증가하곤 합니다. 분류하기 어려운 데이터나 잘못 레이블된 데이터가 들어오면 cost가 증가하곤 합니다.

미니 배치 그레디언트를 할 때 선택해야 할 파라미터는 미니 배치의 크기입니다. 그러면 배치 사이즈는 일반적으로 어떻게 선택되어야 하는지 알아보도록 하겠습니다.
만약 전체 데이터의 크기가 \(m\) 이라고 생각해 보겠습니다. 그러면 한번에 처리할 수 있는 데이터의 크기는 최소 1개에서 최대 m개 까지 처리할 수 있습니다.
위 슬라이드를 보면 극단적으로 처리해야 할 데이터의 크기를 m개 또는 1개인 경우로 나누어서 설명을 해놓았습니다. 이 때, 데이터의 크기가 m이면 batch gradient descent이고 1개이면 stochastic gradient descent라고 합니다.
따라서 배치 그레디언트 디센트의 경우 1개의 배치가 모든 데이터를 포함하게 되고 스토캐스틱 그래디언트 디센트의 경우 m개의 배치가 존재하게 됩니다.
결과적으로 배치/스토캐스틱 그래디언트 디센트 모두 지양하게 되고 미니 배치 그래디언트 디센트를 지향해야 하는 데 그 이유에는 배치/스토캐스틱 그래디언트 디센트의 단점에 큰 이유가 있습니다.
- 먼저 스토캐스틱 그래디언트 디센트의 경우 슬라이드 왼쪽 아래의 학습 형태를 보면 진동이 너무 심하게 됩니다. 당연하게도 데이터 별로 성향이 천차만별이기 때문입니다.
- 또한 데이터를 1개씩 처리하다 보니 벡터라이제이션을 사용하지 못한다는 단점이 크게 작용하여 수행 속도에 영향을 미치게 됩니다. 한번에 처리할 수 있는 데이터의 양이 1개이니 m번 연산을 해야 하는 단점이 전체 수행 속도를 느리게 만들어 버립니다.
- 반면 배치 그래디언트 디센트의 경우 모든 데이터를 한번에 반영하여 학습을 하는 것이기 때문에 1개의 이터레이션이 너무 시간이 오래걸립니다. 그리고 1 epoch 마다 1번의 학습 밖에 되지 않아 학습 속도도 느린 단점이 있습니다.
극단적인 배치/스토캐스틱 그래디언트 디센트가 아닌 배치의 크기 기준으로 두 방법의 사이에 있는 미니 배치 그래디언트 방법을 사용하면 오히려 양쪽의 장점을 가져올 수 있습니다.
- 먼저 데이터 전체는 아니지만 다수의 데이터를 대상으로 그래디언트 디센트를 하게 되므로 벡터라이제이션연산을 할 수 있어서 수행 속도가 빨라지는 장점을 가질 수 있습니다.
- 또한 데이터 전체가 학습 하기 이전에 일부 만으로 학습을 할 수 있어 학습 속도가 빨라지게 됩니다.
그러면 1과 m 사이의 값 중 어떤 값을 선택하는 것이 좋을 까요?

먼저 데이터 셋의 크기를 살펴본 뒤 데이터 셋의 크기가 작다면 그냥 배치 그래디언트 디센트 방법을 사용하는 것을 추천합니다. (데이터 크기가 약 2천개 미만)
- 데이터 크기가 작다면 미니 배치 그래디언트 디센트의 장점을 크게 살릴 수 없고 배치 그래디언트 디센트 방법을 사용하더라도 충분히 학습 속도가 빠릅니다.
만약 데이터의 크기가 어느 정도 크다면 미니 배치 그래디언트 디센트 방법을 사용하는것을 추천합니다.
이 때 일반적으로 사용하는 배치 크기는 64, 128, 256, 512 와 같은 크기 입니다.
왜냐하면 컴퓨터 메모리가 배치되어 있는 방식과 접속되는 방법에 따라 2의 지수승의 배치 크기일 때 더 빨리 실행됩니다.
처음 부터 가장 적합한 배치 사이즈를 알기는 어렵습니다. 따라서 새로운 학습을 할 때 여러 경우의 배치 크기를 접목해 본 뒤 적합한 배치 크기를 사용해 보시길 추천 드립니다.

다음 글 : Exponentially Weighted Averages