
3.1. Conditional random fields - motivation
2000, Jan 01
- 참조 자료 : http://info.usherbrooke.ca/hlarochelle/ift725/3_01_motivation.pdf
- 강의 : https://youtu.be/GF3iSJkgPbA?list=PL6Xpj9I5qXYEcOhn7TqghAJ6NAPrNmUBH
- 이 강의에서는 conditional random field를 위한 워밍업 단계로 컨셉에 대하여 살펴보도록 하겠습니다.
- conditional random field에서는 입력값이 단순히 한 개의 데이터가 아니라
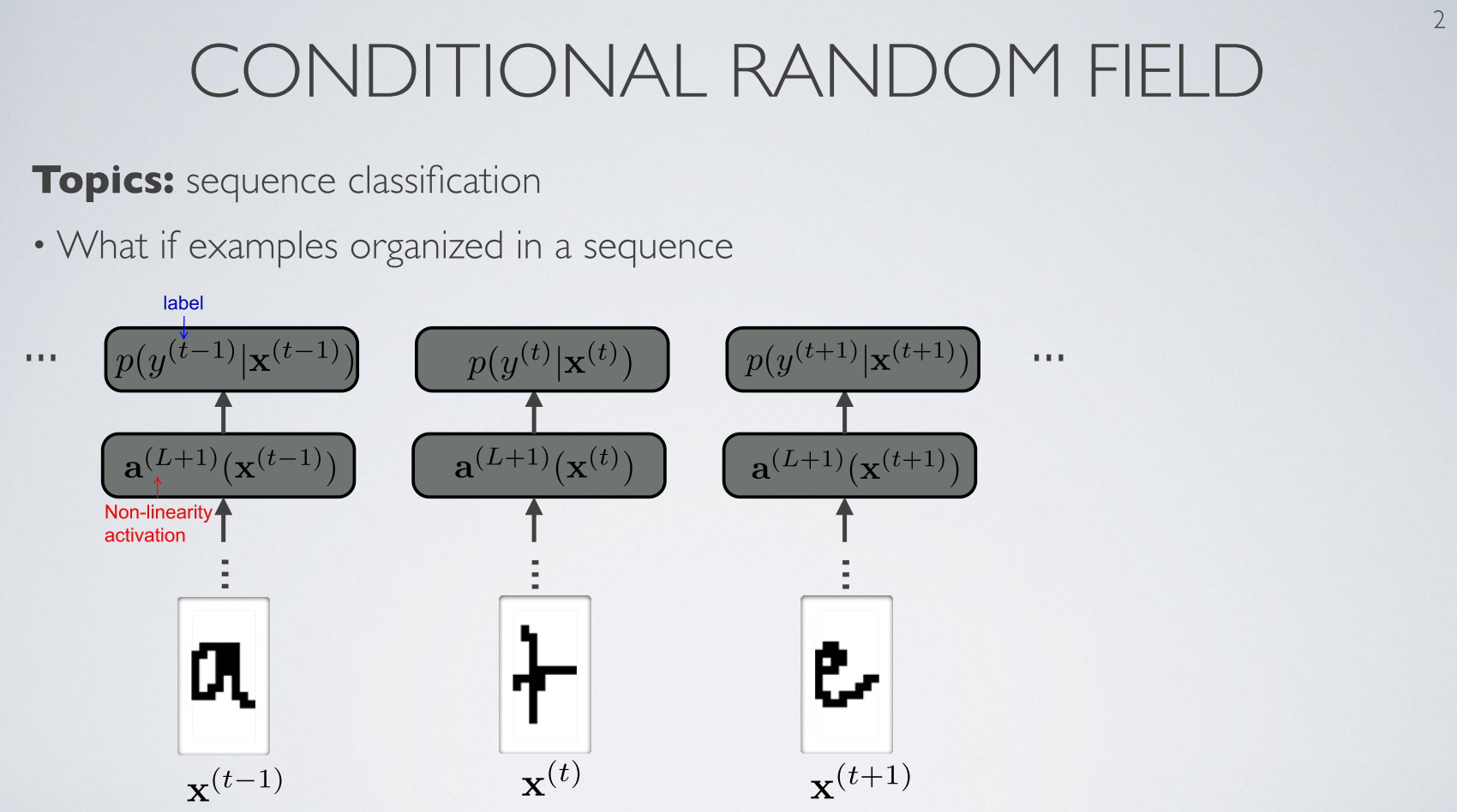
여러 개의 연속적인 데이터인 경우를 가정합니다. - 먼저 위 그림을 보면 입력값인 \(X\)의 첨자 \(t\)를 통해 연속적인 데이터 임을 알 수 있습니다.
- 가장 왼쪽의 \(X^{(t-1)}\)부터 살펴보면 입력은 뉴럴 네트워크인 Non-linearity activation 거쳐 출력을 만듭니다.
- 이 출력은 입력 \(X^{t-1}\) 에 대한 라벨 \(y^{(t-1)}\)의 확률 분포인 \(p(y^{(t-1)} \vert x^{(t-1)})\) 를 나타냅니다.
- 마찬가지로 연속적인 데이터가 입력으로 들어오는 상황에서 \(x^{t}\)가 입력으로 들어오면 \(p(y^{(t)} \vert x^{(t)})\)의 확률 분포를 가집니다.
- 어떤 데이터를 사용하느냐에 따라서 위와 같은 연속적인 데이터를 처리하는 것이 의미가 있을 수도 있고 없을 수도 있습니다.
- 예를 들어 텍스트 같은 경우에는 어떤 단어 뒤에는 또 다른 어떤 단어가 나올 확률이 높을 수 있습니다. 비디오 같은 경우의 각 프레임도 연속적인 데이터 케이스라고 볼 수 있습니다.
- 하지만 위 슬라이드 처럼 단순히 연속적인 데이터를 받아서 각각 처리하면 의미가 없습니다.
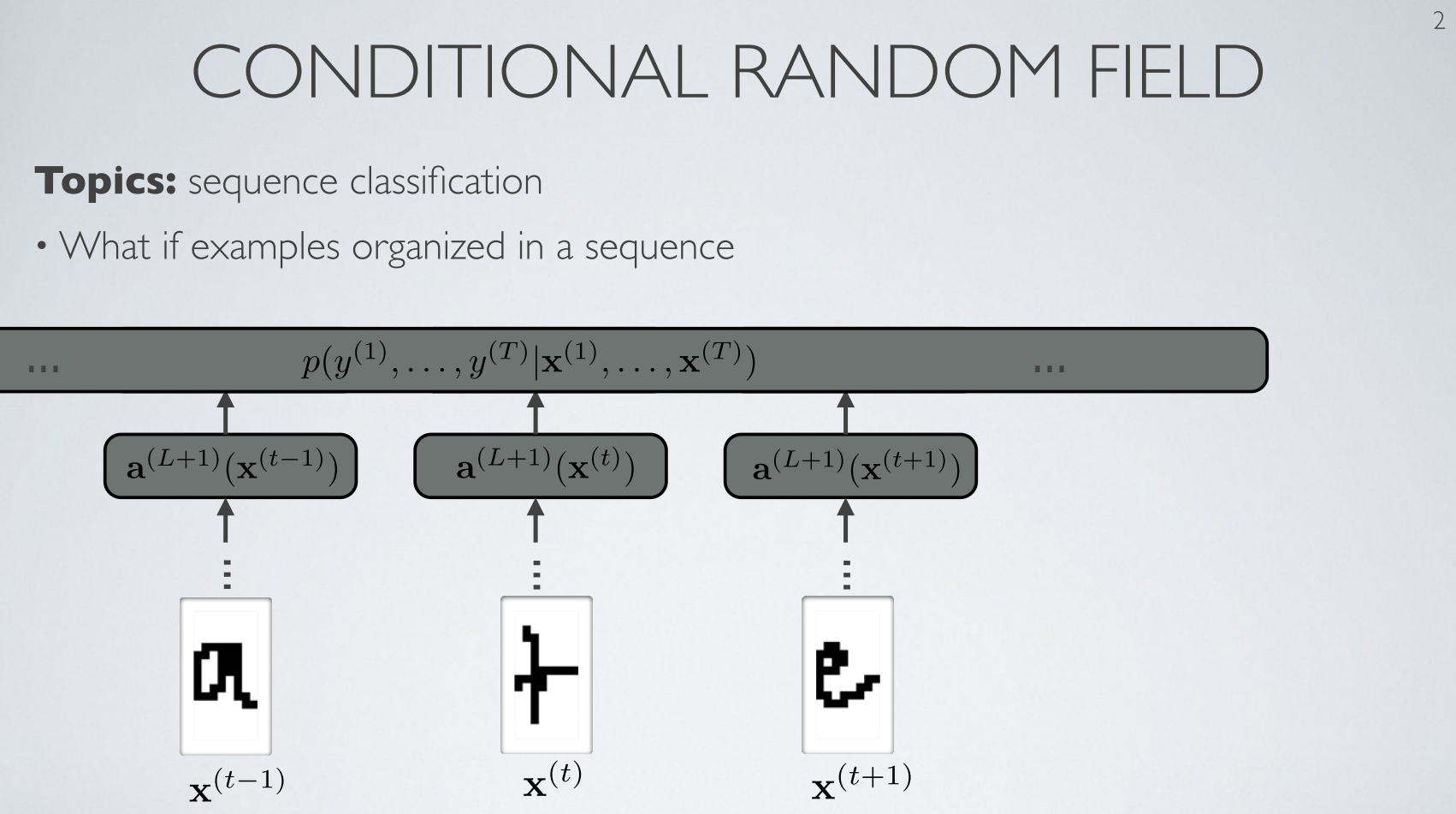
- 반면 위 슬라이드와 같이 연속적인 데이터 전체에 대한 결합 분포를 만들어서 연속적인 데이터가 주어지면 그 데이터에 해당하는 라벨들에 대한 확률 분포를 계산합니다.
- 이 과정은 단순히 각각의 데이터에 대한 분포를 얻어서 그 결과를 합치는 것과는 다릅니다.
- 이 컨셉이
conditional random field의 기본적인 방향이 됩니다.

- 위 슬라이드의 표기법을 보면 \(X^{(t)}\)는 \(t\) 번째 연속적인 데이터를 뜻하고 \(y^{(t)}\)는 \(X^{(t)}\)의 각 데이터에 대응하는 라벨이라 할 수 있습니다.
- 만약 데이터가 이미지라면 연속적인 데이터는 이미지 전체가 되고 세부적인 각각의 데이터는 픽셀이 됩니다. 각 픽셀에 대응하는 라벨은 픽셀이 의미하는 라벨에 해당합니다.
- 그리고 \(K_{t}\)는 각 연속적인 데이터의 길이에 해당합니다. 이미지를 예를 들어 계속 설명하면 이미지 픽셀 갯수인 이미지 크기에 해당합니다.
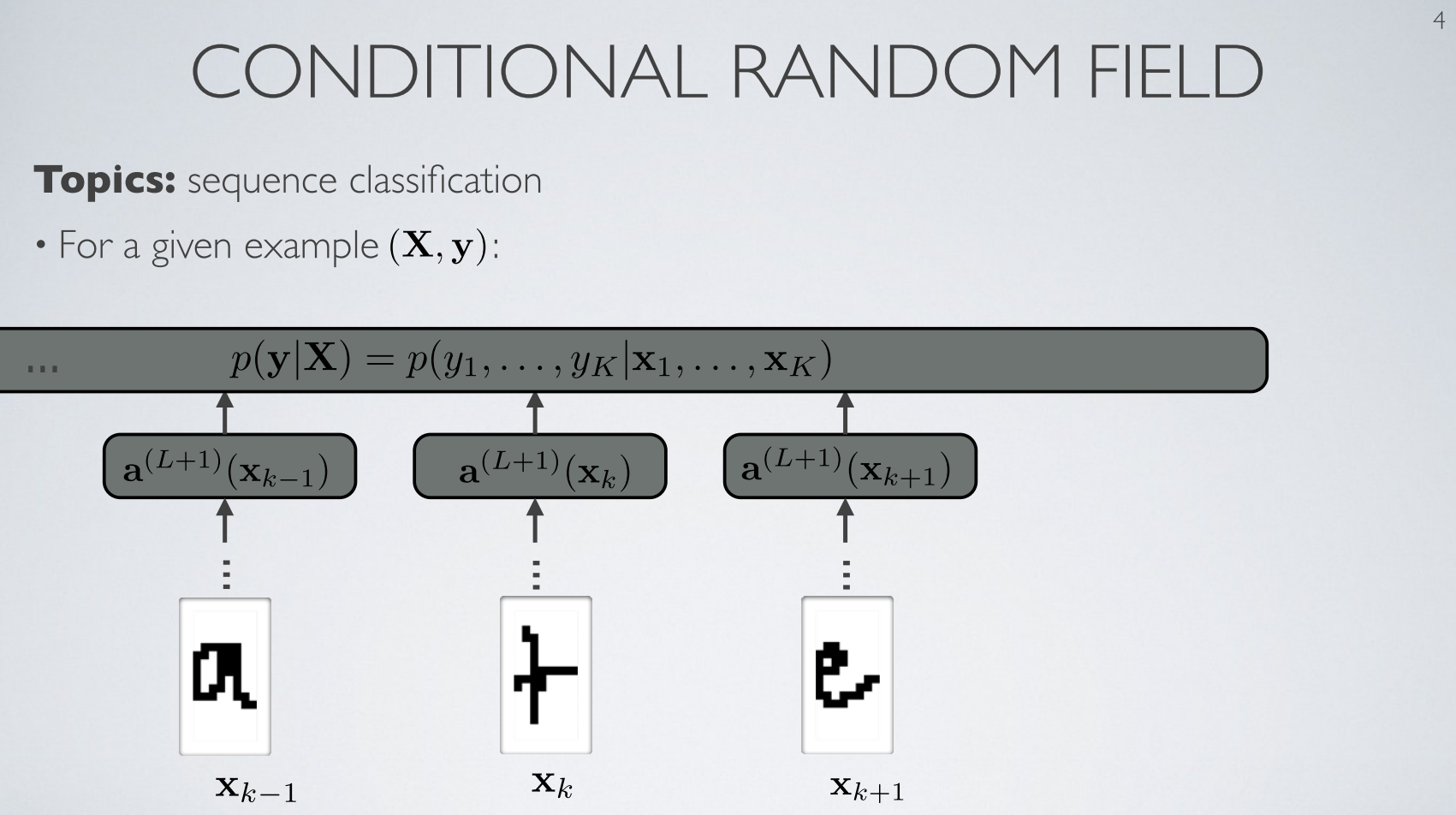
- 앞에서 다룬 슬라이드를 최종 정리하면서 간단하게 표현하였습니다.
- 지금까지 다룬 내용이 앞으로 다룰 conditional random field의 기본 컨셉이며 다음 글에서는 Linear Chain CRF에 대하여 다루어 보도록 하겠습니다.