Linear Regression with PyTorch

Linear Regression with PyTorch

2019, May 19    
  • 출처 : https://github.com/GunhoChoi/PyTorch-FastCampus
  • 이번 글에서는 Pytorch를 이용하여 Linear regression 하는 방법을 알아보도록 하겠습니다.
  • Linear regression의 의미 보다는 PyTorch에서의 training 과정을 어떻게 구현하면 되는지를 초점으로 살펴보면 되겠습니다.

텐서와 자동 미분

  • 텐서에는 requires_grad 라는 속성이 있어서 이 값을 True로 설정하면 자동 미분 기능이 활성화 됩니다.
  • Neural Net에서는 파라미터나 데이터가 모두 이 기능을 사용합니다.
  • requires_grad가 적용된 텐서에 다양한 계산을 하게 되면 계산 그래프가 만들어 지며, 여기에 backward 메소드를 호출하면 그래프가 자동으로 미분을 계산합니다.
    • requires_grad = True가 적용된 텐서에 한하여 backprop이 계산되기 때문에 학습이 필요한 파라미터에 requires_grad = True를 적용하면 됩니다.
  • 다음 식은 \(L\) 을 계산해서 \(a_{k}\)로 미분하는 예제입니다.
    • 　\(y_{i} = \mathbb a \cdot x_{i}, \ \ L = \sum_{i} y_{i}\)
    • 　\(\frac{\partial L}{\partial a_{k}} = \sum_{i} x_{ik}\)
  • 이 작업을 자동 미분으로 구해보도록 하겠습니다.
x = torch.randn(100,3)

# 미분할 변수로 사용되는 학습 파라미터는 requires_grad=True 로 설정합니다.
a =  torch.tensor([1,2,3.], requires_grad = True)

# 계산 그래프를 생성합니다.
y = torch.mv(x,a)
o = y.sum()

# 미분을 실행합니다. 이 때 requires_grad=True로 설정되어 있는 파라미터 a는 backprop이 실행 됩니다.
o.backward()

a.grad
: tensor([18.5806, -4.1716, -0.1735])

x.sum(0)
: tensor([18.5806, -4.1716, -0.1735])


  • 위 식을 보면 마지막의 a.grad와 x.sum(0)의 값이 일치함을 알 수 있습니다.
  • 그 이유는 \(a\)에 대하여 미분한 결과를 합하면 \(x\)를 sum한 결과와 같기 때문입니다.
  • Neural Network에서 처럼 Chain rule이 적용이 되면 위와 같은 자동 미분의 역할을 매우 중요해집니다.



파이토치로 선형 회귀 모델 만들기(직접 만들기)

  • 파이토치를 사용해서 선형 회귀 모델의 파라미터를 구해보도록 하겠습니다. 다음과 같이 변수가 두 개인 모델을 생각할 수 있습니다.
    • 　\(y = 1 + 2x_{1} + 3x_{2}\)
  • 먼저 랜덤값을 이용하여 노이즈를 일부러 섞어서 학습 데이터를 만들어 보겠습니다.
import torch

# Ground Truth 계수
w_true = torch.Tensor([1,2,3])

# X 데이터를 준비 합니다. 
# 편을 회귀 계수에 포함시키기 위해 X의 최소 차원에 1을 추가합니다.
X = torch.cat([torch.ones(100, 1), torch.randn(100, 2)] , 1)

# GT 계수와 각 X의 내적을 행렬과 벡터의 곱으로 모아서 계산합니다.
y = torch.mv(X, w_true) + torch.randn(100) * 0.5

# Gradient Descent로 최적화 하기 위하여 파라미터 Tensor를 난수로 초기화 생성합니다.
w = torch.randn(3, requires_grad=True)

gamma = 0.1


  • 데이터(X) 및 변수(w)를 준비하였으니 gradient descent로 파라미터를 최적화 해보겠습니다.
# 손실 함수의 로그
losses = []

# 100회 반복
for epoch in range(100):
    # weight의 gradient 초기화
    w.grad = None
    
    # 선형 모델로 y 예측값을 계산
    y_pred = torch.mv(X, w)
    
    # MSE loss와 w에 의한 미분을 계산
    loss = torch.mean((y-y_pred)**2)
    loss.backward()
    
    # gradient를 갱신하기 위해 w의 data를 업데이트 합니다.
    w.data = w.data - gamma * w.grad.data
    
    # 수렴을 확인하기 위하여 loss를 기록해 둡니다.
    losses.append(loss.item())


  • 최적화가 제대로 이루어지면 손실 함수가 수렴하는 지 알 수 있습니다.

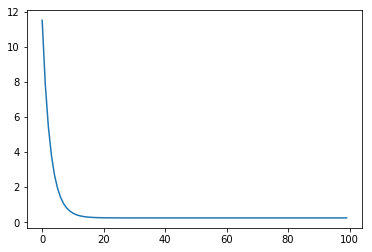
Drawing

  • w값을 살펴보면 다음과 같습니다
tensor([0.9656, 2.0326, 3.0433], requires_grad=True)
  • 처음 설정한 1, 2, 3 값에 거의 유사합니다.



파이토치로 선형 회귀 모델 만들기(nn, optim 모듈 사용)

  • 앞에서는 자동 미분을 사용할 때 이외에는 모델 구축 및 gradient descent 모두 직접 하였습니다.
  • 파이토치를 이용하면 쉽게 할 수 있습니다.
    • 모델의 구축은 torch.nn
    • 최적화는 torch.optim을 이용합니다.
  • 데이터 생성은 앞에서 사용한 코드를 그대로 이용합니다.
  • 아래 코드에서 nn.Linear 이름에서 알 수 있듯이, 선형 결합을 계산하는 클래스로 feature, bias등을 가지고 있습니다.
  • 그리고 optimizer와 nn.Linear를 연계하여 학습 결과 파라미터를 저장하는등의 처리를 할 수 있습니다.
  • nn.MSELoss는 MSE를 계산하기 위한 클래스입니다.
from torch import nn, optim

# Linear층을 작성 합니다.
net = nn.Linear(in_features=3, out_features=1, bias = False)

# optimizer의 SGD를 사용하여 최적화 합니다.
optimizer = optim.SGD(net.parameters(), lr = 0.1)

# MSE loss 클래스
loss_func = nn.MSELoss()

losses = []

for epoch in range(100):
    # 이전 epoch의 backward로 계산된 gradient값을 초기화
    optimizer.zero_grad()
    
    # 선형 모델로 y 예측값을 계산
    y_pred = net(X)
    
    # MSE loss 계산
    # y_pred는 (n,1)과 같은 shape을 가지고 있으므로 (n,)로 변경할 필요가 있습니다.
    loss = loss_func(y_pred.view_as(y), y)
    
    # loss의 w를 사용한 미분 계산
    loss.backward()
    
    # gradient를 갱신합니다.
    optimizer.step()
    
    # 수렴 확인을 위하여 loss를 기록해 둡니다.
    losses.append(loss.item())


  • 수렴한 모델의 파라미터를 확인해 보면 다음과 같습니다.
list(net.parameters())
: [Parameter containing:
 tensor([[0.9656, 2.0326, 3.0433]], requires_grad=True)]


  • 학습이 잘 된것을 볼 수 있습니다.
Twitter Facebook Google+
# pytorch # linear regression