신호와 시스템 (Signal and System)

2021, Feb 16    

• Signal and System 목차

• 참조 : Signals and Systems 2nd Edition (Alan Oppenheim)

목차

• 신호와 시스템의 정의

• 연속 시간 신호와 이산 시간 신호

• 독립 변수의 변환

• 지수 신호와 정현파 신호

• 단위 임펄스 및 단위 계단 함수

• 연속 시간 및 이산 시간 시스템

• 기본적인 시스템 특성

신호와 시스템의 정의

• 이번 글에서는 신호와 시스템의 기본적인 개념에 대하여 배워 보도록 하겠습니다
• 먼저 이번 글에서 다룰 신호와 시스템의 정의를 살펴 보겠습니다
• 신호는 송수신간의 약속된 정보를 뜻하며 신호의 반대되는 말은 노이즈(잡음)입니다. 즉, 노이즈에는 송수신간 약속된 정보가 들어있지 않습니다
• 시스템은 신호를 처리하는 것을 소프트웨어 또는 하드웨어를 뜻합니다.

연속 시간 신호와 이산 시간 신호

• 신호는 대표적으로 연속 시간의 신호와 이산 시간의 신호로 나뉘게 됩니다.
• 신호를 나타낼 때, 가로축은 시간(t)을 나타내고 세로축은 시간에 따른 신호의 진폭을 나타냅니다.

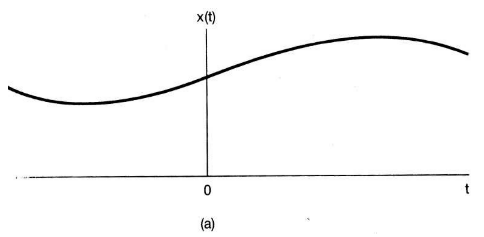
• 먼저 연속 시간 신호에서는 시간과 진폭이 모두 연속적인 값을 가집니다. 흔히 말하는 아날로그 신호를 뜻합니다.
• 예를 들어 흔히 사용되는 마이크가 입력되는 소리를 연속 시간의 신호로 바꾼 아날로그 신호입니다. 이 때, 이 아날로그 신호를 처리하는 것이 아날로그 시스템입니다.
• 이러한 아날로그 신호를 표현할 때, 가로 축 시간은 \(t\)로 표현하고 세로축 진폭은 \(x(t)\)로 표현하도록 하겠습니다.

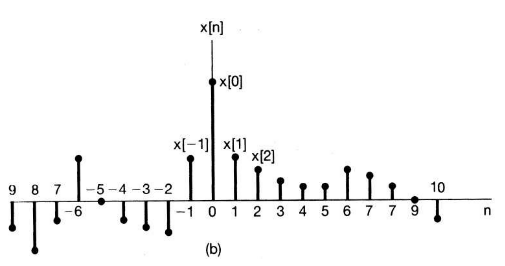
• 반면 이산 시간 신호는 시간 축이 불연속적인 값을 가집니다. 위 그래프와 같이 가로축의 값이 정수 단위로 끊어져 있습니다.
• 이는 연속 시간 신호에서 시간 축을 기준으로 표본화(Sampling)을 거쳐서 이산 시간 신호의 값으로 표현합니다.
• 이산 시간 신호에서의 시간 값은 정수이므로 \(n\)으로 표기하겠습니다. 그리고 진폭의 값은 \(x[n]\)으로 나타내어 연속 시간의 신호 값과 차이를 두도록 하겠습니다.

• 이산(Discrete) 시간 신호와 간혹 디지털(Digital) 신호에 대하여 헷갈릴 수 있습니다. 디지털 신호는 이산 시간 신호에서 양자화와 부호화 과정을 거친 신호를 뜻합니다.
• 먼저 앞에서 설명한 바와 같이 이산 시간 신호는 연속 시간 신호 → 샘플링를 뜻합니다.
• 반면 디지털 신호는 연속 시간 신호 → 샘플링 → 양자화(quantization) → 부호화(encoding)까지 거친 신호를 뜻합니다.
• 양자화는 연속/이산 시간 신호에서 신호의 진폭 값이 실수인데 이를 정수로 나타내는 것을 뜻합니다.
• 부호화는 정보의 형태나 형식을 표준화, 보안, 처리 속도 향상, 저장 공간 절약 등을 위해서 다른 형식으로 변환하는 처리를 뜻합니다.

• 지금까지 연속 및 이산 시간 신호의 뜻에 대하여 알아보았습니다. 이번에는 각 신호의 총 에너지, 평균 전력에 대하여 알아보도록 하겠습니다.
• 먼저 기본적인 에너지와 전력에 관련된 공식들을 나열해 보겠습니다.

• \(P = v * i = R*i^{2} = \frac{v^{2}}{R}\) (전력에 관한 전압, 전류, 저항의 관계), \(v = R * i\)

• \(w = \int P \ dt = R \int i^{2} \ dt = \frac{1}{R} \int v^{2} dt\) (에너지는 전력 \(P\)의 적분 값)

• \(\frac{dw}{dt} = P\) (에너지와 전력의 관계)

• 앞에서 살펴본 연속/이산 시간 신호에서의 세로축인 진폭은 신호의 크기나 세기를 나타내며 단위는 v(전압) 입니다.
• 이 점을 이용하여 아래 연속 시간 신호에서의 신호 세기인 \(x(t)\)와 이산 시간 신호에서의 신호 세기인 \(x[n]\)을 이용하여 에너지 및 전력을 수식으로 어떻게 나타내는 지 살펴보도록 하겠습니다.

연속 시간 신호에서의 에너지 및 전력

• 먼저 연속 시간 신호에서의 에너지 및 전력에 대하여 알아보도록 하겠습니다.
• 앞에서 설명한 바와 같이 에너지는 전력의 적분값을 이용하고 전력은 전압, 전류, 저항을 이용하여 나타낼 수 있습니다.

• ① \(t_{1} \le t \le t_{2}\) 에서의 총 에너지 : \(\int_{t_{1}}^{t_{2}} \vert x(t) \vert^{2} dt\)

• ② \(t_{1} \le t \le t_{2}\) 에서의 평균 전력 : \(\frac{1}{t_{2} - t_{1}} \int_{t_{1}}^{t_{2}} \vert x(t) \vert^{2} dt\)

• ③ \(-\infty \le t \le \infty\) 에서의 총 에너지 : \(E_{\infty} = \lim_{T \to \infty}{\int_{t_{1}}^{t_{2}} \vert x(t) \vert^{2} dt} = \int_{-\infty}^{\infty} \vert x(t) \vert^{2} dt\)

• ④ \(-\infty \le t \le \infty\) 에서의 평균 전력 \(P_{\infty}\) : \(P_{\infty} = \lim_{T \to \infty}{\frac{1}{2T} \int_{t_{1}}^{t_{2}} \vert x(t) \vert^{2} dt}\)

• 먼저 ①, ③을 구할 때에는 \(w = \frac{1}{R} \int v^{2} dt\)에서 \(R = 1\)로 가정한 상태의 식을 적용하였습니다.
  • 왜냐하면 에너지(힘:w)의 개념 즉, 변화량에 대한 적분을 하는 개념에서 시간(t) 함수는 전류(i)와 전압(v)에는 관계되지만 저항(R)은 시간의 변화와 관련없기 때문에 상수값 1로 가정할 수 있습니다.
• ②, ④에서는 \(dw / dt = P\)를 이용하여 식을 전개하였습니다. 즉, 시간 구간인 \(t2 - t1\)이 시간 변화량 \(dt\)와 같이 적용되었습니다.

• 이 때, 4개의 식 전체에 사용된 \(\vert x(t) \vert\)는 어떻게 적용된 것일까요?
• 앞에서 설명한 바와 같이 신호의 진폭(v)인 \(x(t)\)의 제곱을 계산에 적용해야 합니다. 복소수의 범위로 보았을 때, 단순한 제곱이 아니라 \(\vert x \vert^{2} = x \cdot \bar{x}\)의 형태로 (\(\bar{x}\)는 켤레 복소수) 제곱을 취해주어야 주어서 실수값으로 만듭니다.. 이 때, 두 값을 정의하면 다음과 같이 정의할 수 있습니다.

• \[x = a + jb\]
• \[\bar{x} = a - jb\]
• \[x \cdot \bar{x} = a^{2} + b^{2} \ \ \because j = \sqrt{-1}, \ \ j^{2} = -1\]
• \[\vert x \vert = \sqrt{a^{2} + b^{2}} \ \ \ \ \cdots \text{absolute value of complex number}\]
• \[\color{blue}{\vert x \vert^{2}} = (\sqrt{a^{2} + b^{2}})^{2} = \color{blue}{x \cdot \bar{x}}\]

• 위 과정을 통하여 만약 \(x(t)\)가 복소수라면 \(\vert x(t) \vert^{2} = x(t) \cdot \bar{x(t)}\)를 통하여 실수화하여 계산에 적용합니다. 만약 \(x(t)\)가 실수라면 단순히 \(x(t)^{2}\)으로 계산을 해도 상관없습니다.

이산 시간 신호에서의 에너지 및 전력

• 이산 시간 신호에서의 에너지 및 전력은 연속 시간 신호에서 사용한 적분을 이산값의 합인 \(\sum\)으로 바꿔서 적용합니다.

• ① \(n_{1} \le n \le n_{2}\) 에서의 총 에너지 : \(\sum_{n=n_{1}}^{n_{2}} \vert x[n] \vert^{2}\)

• ② \(n_{1} \le t \le n_{2}\) 에서의 평균 전력 : \(\frac{1}{n_{2} - n_{1} + 1} \sum_{n=n_{1}}^{n_{2}} \vert x[n] \vert^{2}\)

• ③ \(-\infty \le n \le \infty\) 에서의 총 에너지 : \(E_{\infty} = \lim_{N \to \infty}{\sum_{n=-N}^{N} \vert x[n] \vert^{2} } = \sum_{n=-\infty}^{\infty} \vert x[n] \vert^{2}\)

• ④ \(-\infty \le n \le \infty\) 에서의 평균 전력 \(P_{\infty}\) : \(P_{\infty} = \lim_{N \to \infty}{\frac{1}{2N+1} \sum_{n=-N}}^{N} \vert x[n] \vert^{2}}\)

• 연속/이산 시간 신호에서 구한 \(E_{\infty}\)와 \(P_{\infty}\)의 관계를 보았을 때, 전체 구간에서 에너지와 전력은 다음 관계가 성립함을 알 수 있습니다.
• ① 전체 구간에서 총 에너지가 유한하다면 평균 전력은 0이고 그 역도 성립한다. (\(E_{\infty} \lt \infty \leftrightarrow P_{\infty} = 0\))
• ② 전체 구간에서 총 에너지가 무한하다면 평균 전력은 유한하며 그 역도 성립한다. (\(E_{\infty} = \infty \leftrightarrow P_{\infty} \lt \infty\))

독립 변수의 변환

• 앞에서 다룬 신호에서의 독립 변수는 시간 \(t\) 입니다. 이번에는 시간 \(t\)의 변환을 주었을 때, 신호가 어떻게 달라지는 지 살펴보도록 하겠습니다.
• 대표적으로 시간 변위(time shift), 시간 반전(time reversal), 시간 배율(time scaling), 주기 신호(periodic signal)이 있습니다.

• 먼저 시간 변위에 대하여 살펴보도록 하겠습니다.

• 시간 변위(time shift) : \(x(t) \to x(t - t_{0}), x[n] \to x[ n-n_{0}]\) 에 대하여
  • 만약 \(t_{0} > 0\) 이면, \(x(t - t_{0})\)은 \(x(t)\)의 지연 신호 (또는 과거 신호) 입니다.
  • 만약 \(t_{0} < 0\) 이면, \(x(t - t_{0})\)은 \(x(t)\)의 앞선 신호 (또는 미래 신호) 입니다.

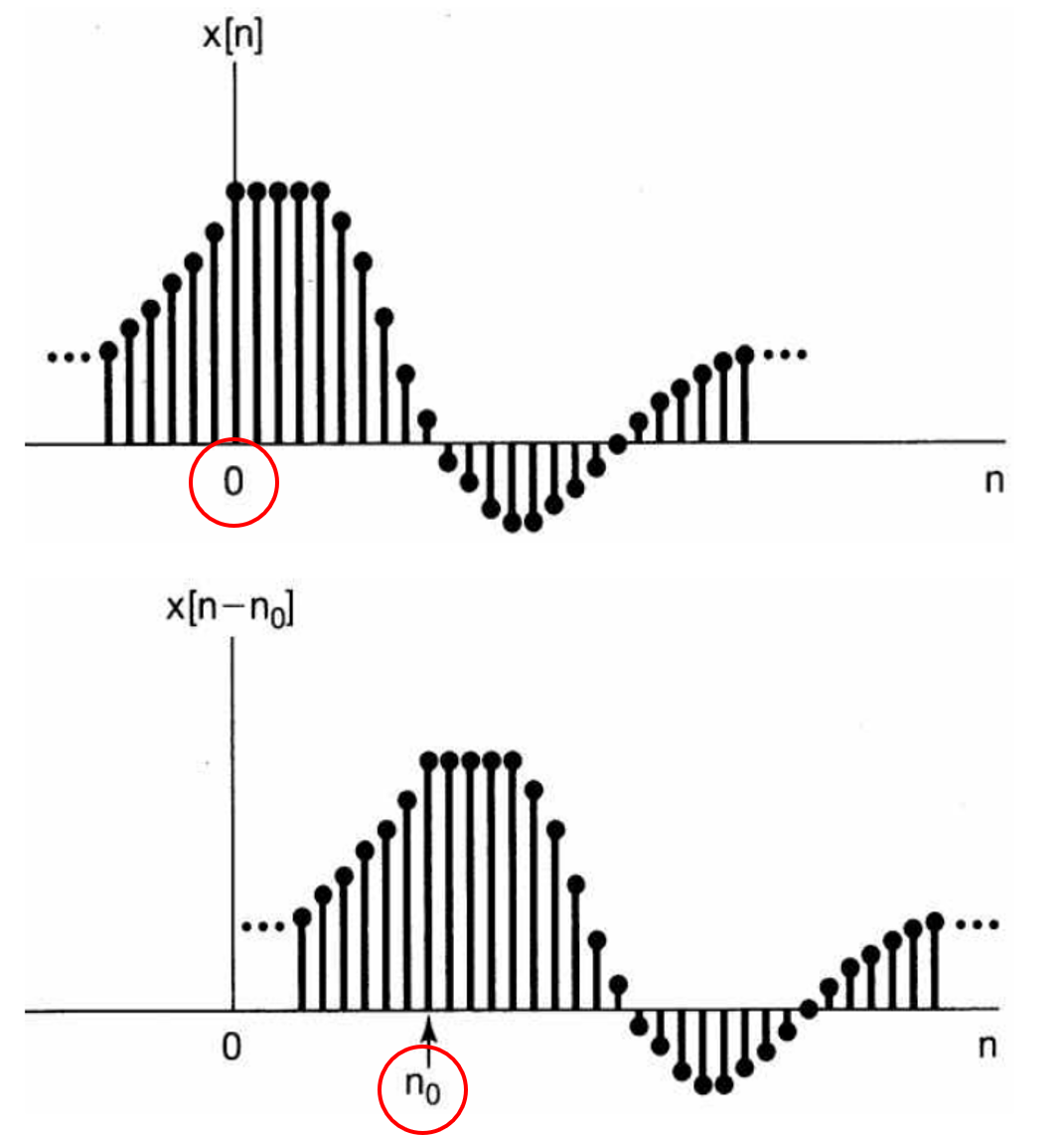
• 위 그래프를 보면 \(n_{0}\)만큼 시간 변위가 발생한 것을 확인할 수 있습니다. 이 때, \(n_{0}\)을 지연 시간 이라고 합니다. 왜냐하면 기존에 시간 0에서 나타났던 신호가 \(n_{0}\) 만큼 지연되어서 신호가 나타났기 때문입니다. 이미 나타난 신호가 지연되어서 나타났기 때문에 과거 신호라고도 부릅니다.
• 앞선 신호 또는 미래 신호라고 불리는 시간 변위는 지연 신호와 반대로 생각하면 됩니다.

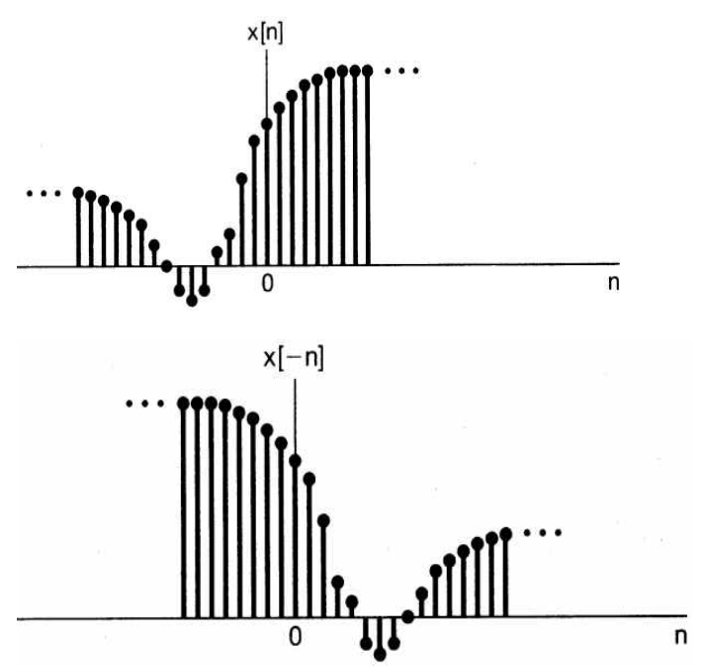
• 시간 반전(time reversal) : \(x(t) \to x(-t), x[n] \to x[-n]\)
  • 　\(x(-t)\)는 \(x(t)\)의 \(t = 0\) (y축) 대칭
  • 　\(x[-n]\)는 \(x[n]\)의 \(n = 0\) (y축) 대칭

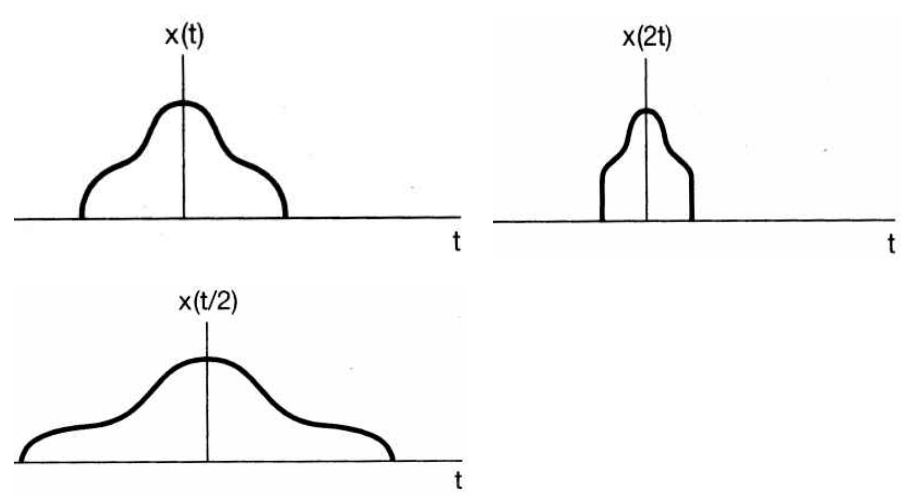
• 시간 배율(time scaling) : \(x(t) \to x(a * t)\)
  • 　\(0 < a < 1\) 일 때, \(x(a*t)\)의 \(t\) 축의 폭이 증가
  • 　\(a > 1\) 일 때, \(x(a*t)\)의 \(t\) 축의 폭이 감소

• 위의 3가지 독립 변수 \(t\)의 변환을 이용하여 아래 예제를 한번 살펴보겠습니다.

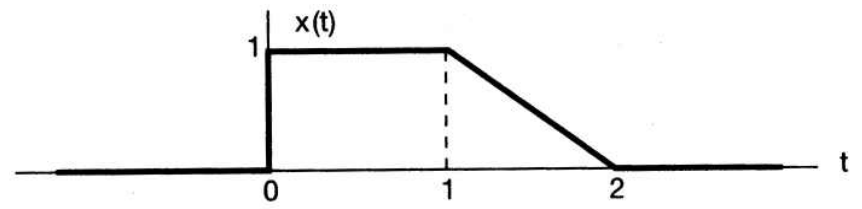
• 먼저 위 신호와 같은 \(x(t)\)가 있을 때, \(t\)의 변화에 따라 어떻게 신호가 바뀌는 지 살펴보도록 하겠습니다.

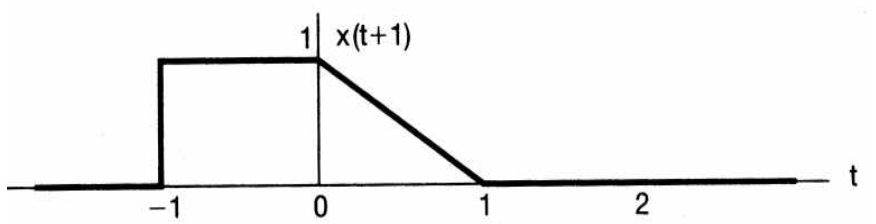
• 위 예제는 \(x(t + 1)\) 입니다.

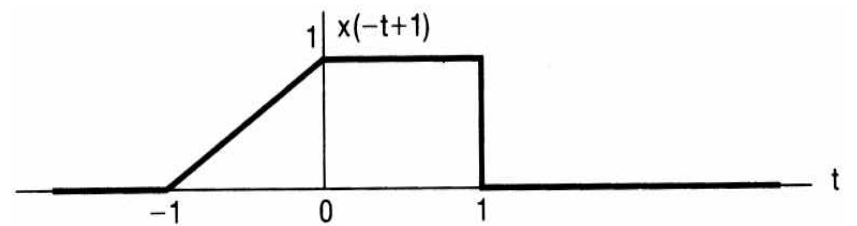
• 위 예제는 \(x(-t +1) = x(-(t - 1))\) 입니다.

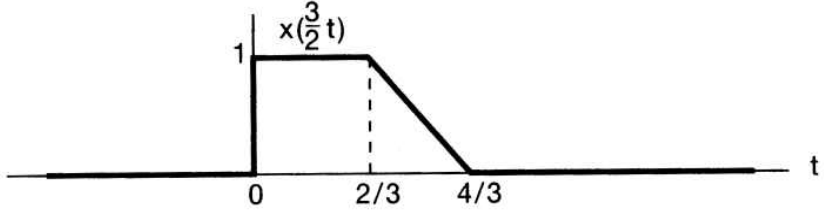
• 위 예제는 \(x(\frac{3}{2}t)\) 입니다.

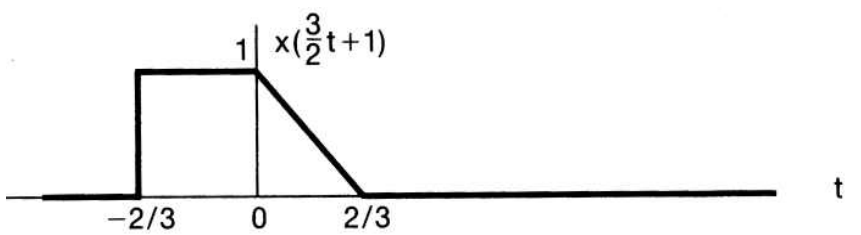
• 위 예제는 \(x(\frac{3}{2}t + 1)\) 입니다.

• 주기 신호(periodic signal) : \(x(t) = x(t + T)\) (주기 \(T\)), \(x[n] = x[n + N]\) (주기 \(N\))

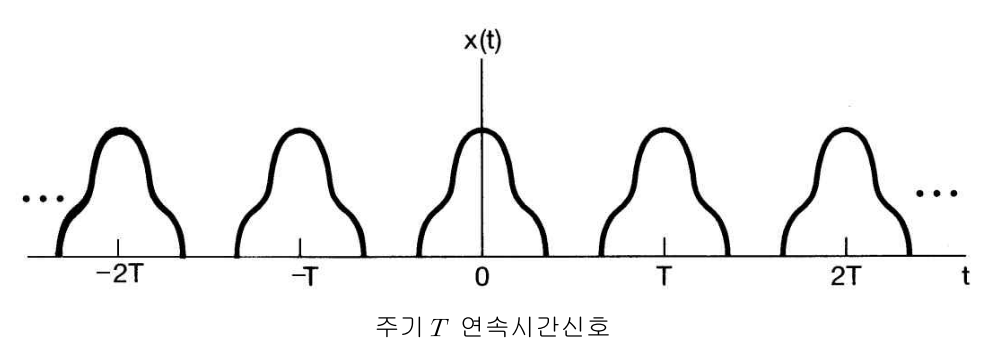
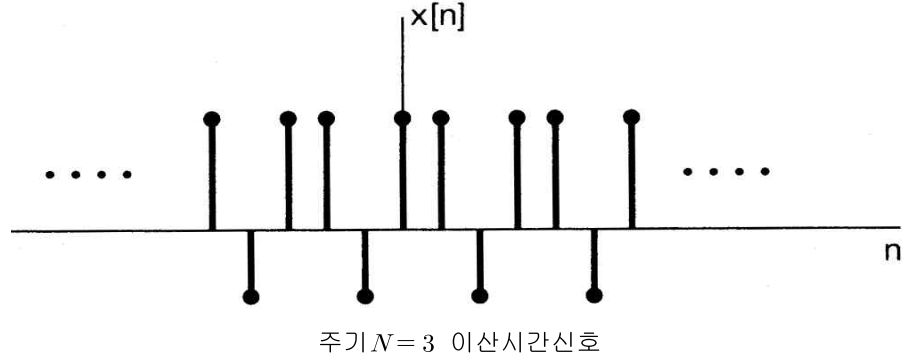
• 마지막으로 시간 축 \(t\)에 대하여 우함수(even function) 신호와 기함수(odd function) 신호에 대하여 알아보도록 하겠습니다.
• 우함수(even function) 신호 : \(x(t) = x(-t)\), \(x[n] = x[-n]\), 세로축(y축) 대칭인 함수
• 기함수(odd function) 신호 : \(x(t) = -x(-t)\), \(x[n] = -x[-n]\), 원점 대칭인 함수

• 임의의 신호 \(x(t)\)에 대하여 다음과 같이 계산을 적용하였을 때, 우함수와 기함수를 만들 수 있습니다.
• 우함수 : \(x_{e}(t) = [x(t) + x(-t)] / 2\), 즉 원래 함수와 y축 대칭인 우함수를 더한 후 2로 나누면 우함수가 생성됩니다.
• 기함수 : \(x_{o}(t) = [x(t) - x(-t)] / 2\), 즉 원래 함수와 원점 대칭인 기함수를 더한 후 2로 나누면 기함수가 생성됩니다.

• \[x(t) = x_{e}(t) + x_{o}(t)\]
• \[x(-t) = x_{e}(t) - x_{o}(t)\]

• 위 식을 통하여 알 수 있는 점은 임의의 함수는 우함수와 기함수의 합으로 표현할 수 있다라는 점입니다.

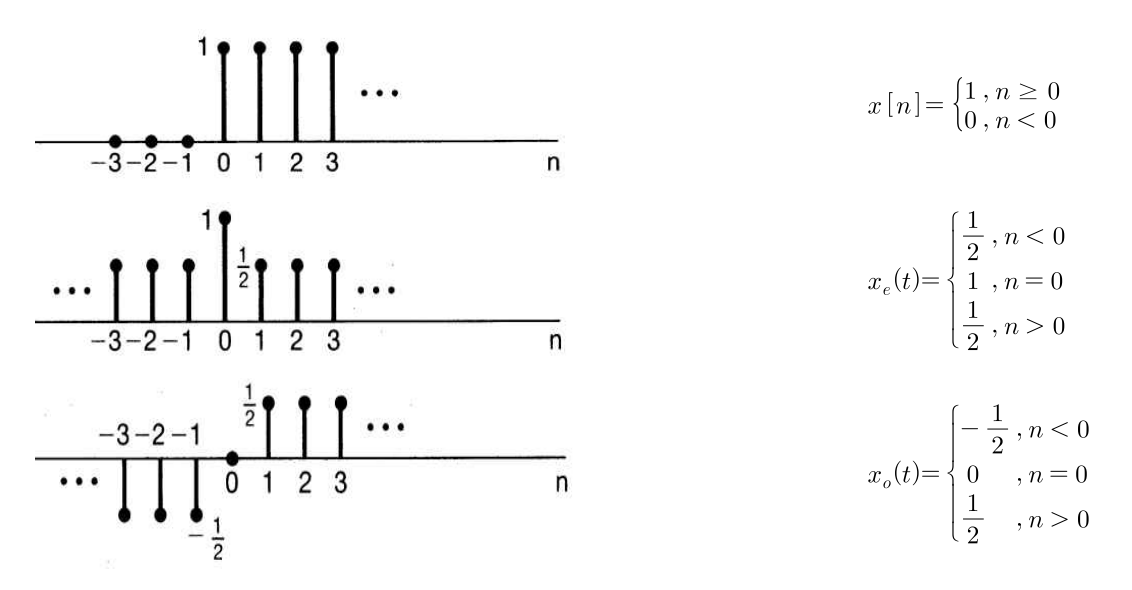
• 첫번째 신호가 원 함수의 신호이고 두번째 신호는 우함수 (\(x(t) = x_{e}(t) + x_{o}(t)\)) 형태로 나타낸 것입니다. 세번째신호는 기함수 (\(x(-t) = x_{e}(t) - x_{o}(t)\))의 형태로 나타내었습니다.
• 위 예제에서 우함수와 기함수 형태의 이산 시간 신호를 각 시간 단위 별로 더하면 기존의 \(x(t)\)로 나타내집니다. 즉, 임의의 함수를 우함수와 기함수의 합으로 표현한 것 입니다.

지수 신호와 정현파 신호

• 앞에서 신호의 정의에 대하여 살펴 보았습니다. 이번에는 신호의 기본이 되는 sin, cos 정현파 신호와 이를 지수 형태로 나타내는 지수 신호에 대하여 다루어 보도록 하겠습니다.

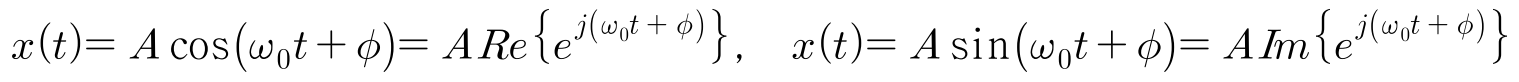
• 위 식의 Re는 실수값을 의미하고 Im는 허수값을 의미합니다. 즉, 지수 형식으로 표현된 값을 실수값을 취하면 cos가 되고 허수값을 취하면 sin이 됨을 뜻합니다. 왜냐하면 지수함수가 sin, cos으로 분해가 되는 오일러 공식을 따르기 때문입니다.

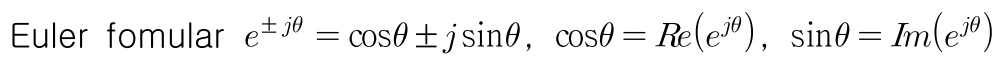
• 위 오일러 공식에 따라 지수 함수 \(e^{\pm j\theta} = \cos{\theta} \pm j\sin{\theta}\) 와 같이 전개되므로 이 원리를 이용하여 \(A\cos{w_{0}t + \phi} = A \ Re\{e^{j(w_{0}t + \phi)} \}\)와 \(A\sin{w_{0}t + \phi} = A \ Im\{e^{j(w_{0}t + \phi)} \}\)를 유도할 수 있습니다.

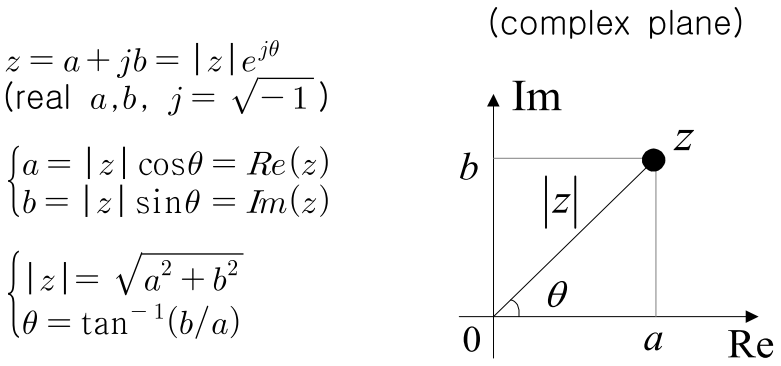
• 오일러 공식에 의한 주기 함수와 cos, sin 함수의 관계와 더불어 복소 평면 상에서의 cos, sin 함수의 관계를 살펴 보겠습니다.
• 위 그래프에서 가로축은 실수부이고 세로축은 허수부입니다. 이 때 \(z\)를 직각 좌표계와 극 좌표계로 나타낼 수 있습니다.
• 　\(z = a + jb = \vert z \vert e^{j\theta}\) (가운데 식이 직각 좌표계이고 지수 함수 형태의 식이 극 좌표계입니다.)
• 그리고 \(z\)의 크기인 절대값은 삼각형의 대각선인 \(\vert z \vert\)가 되는 것을 알 수 있습니다. 이 값을 이용하여 cos, sin 함수를 나타내 보겠습니다.

• \[a = \cos{\theta} \vert z \vert\]
• \[b = \sin{\theta} \vert z \vert\]
• \[z = a + jb = \cos{\theta} \vert z \vert + j(\sin{\theta} \vert z \vert) = \vert z \vert (\cos{\theta} + j \sin{\theta}) = \vert z \vert e^{j\theta} \ \ \because \text{euler formula}\]

• 이와 같은 방법으로 \(z\)를 직각 좌표계와 극 좌표계 방식으로 나타낼 수 있습니다.

• 다음으로 정현파 신호에 대한 성질을 살펴보도록 하겠습니다.

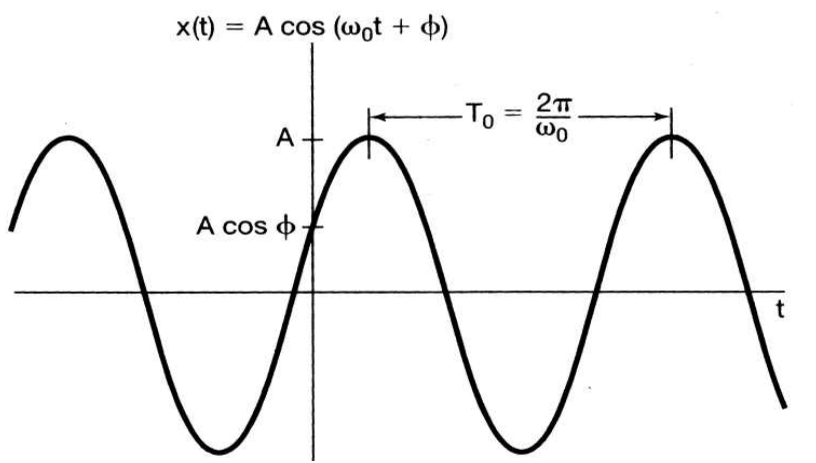
• 주기(period), 1 사이클 시간 (단위 : sec) : \(T_{0} = \frac{2 \pi}{w_{0}}\)
• 주파수(frequency), 1 초 내 싸이클 수 (단위 : Hz) : \(f_{0} = \frac{1}{T_{0}}\)
• 각 주파수(radian frequency) : \(w_{0} = 2 \pi f_{0}\)
• 진폭(amplitude), 또는 peak : \(A\)
• 위상(phase) (단위 : radian) : \(\phi\)

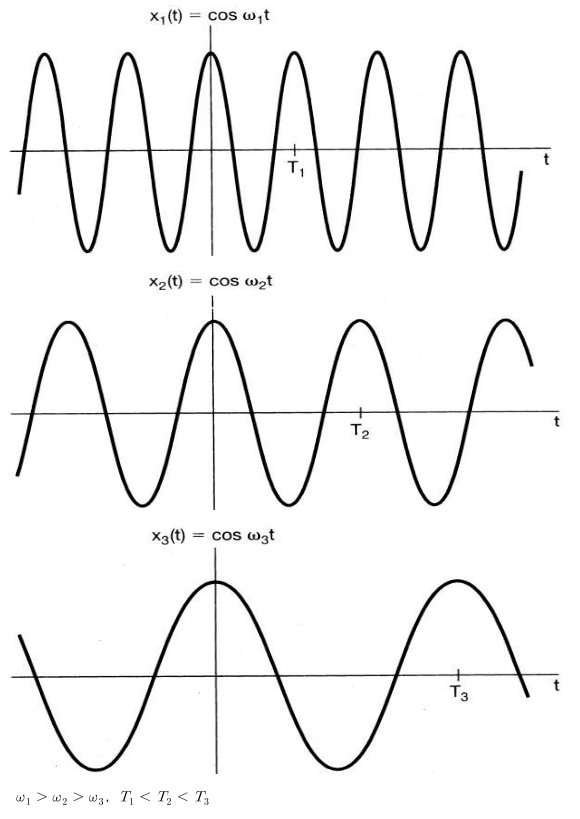
• 위 그래프를 살펴보면 \(T_{1} \lt T_{2} \le T_{3}\)이므로 주기는 점점 늘어나고 \(w_{1} \gt w_{2} \gt w_{3}\) 이므로 주파수는 점점 감소하는 것을 확인할 수 있습니다.

단위 임펄스 및 단위 계단 함수

• 이번에는 가장 기본적인 신호인 단위 임펄스 함수와 단위 계단 함수에 대하여 알아보도록 하겠습니다. 이 함수도 연속 시간과 이산 시간 각각의 표현 방법이 다르므로 이를 분리하여 배워보겠습니다.

• 먼저 이산 시간에 대한 두 함수의 의미를 살펴보겠습니다.
• 이산 시간에서 단위 임펄스 (단위 샘플) 함수는 다음과 같습니다.

• \[\delta[n] = \begin{cases} 0, \ n \neq 0 \\ 1, \ n = 0 \end{cases}\]

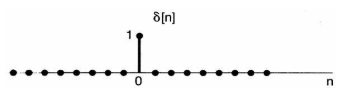
• 단위 임펄스 함수의 기본형은 위 식을 따르고 앞에서 다룬 독립 변수 시간의 변화에 따라서 다양하게 변형할 수 있습니다.
• 예를 들어 \(2 \delta[n], 2\delta[n-4], 2\delta[n+2]\) 등과 같이 시간 변위 및 배율을 줄 수 있습니다.

• 다음은 이산 시간에서의 단위 계단(Unit Step) 함수에 대하여 알아보도록 하겠습니다.

• \[u[n] = \begin{cases} 0, \ \ n \lt 0 \\ 1, \ \ n \ge 0 \end{cases}\]

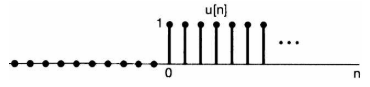
• 위 함수는 단위 임펄스 함수의 확장이라고 볼 수 있습니다. 따라서 두 함수는 다음 식과 같은 관계를 가집니다.

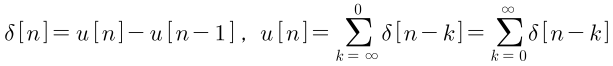
• 먼저 위 식은 단위 계단 함수를 이용하여 단위 임펄스 함수를 표현한 예시 입니다. \(u[n]\)과 \(u[n-1]\)을 이용하면 단위 임펄스 함수를 만들 수 있습니다.
• 이후에 이와 관련된 식을 다룰 예정이며 이를 차분 방정식이라고 합니다.

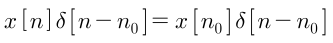
• 두번째 식은 단위 임펄스 함수의 성질을 이용한 것입니다. 즉, 하나의 값 이외에는 모두 0으로 만들어 버리는 성질을 이용한 것입니다.
• 임의의 함수 \(x[n]\)에 대하여 \(x[n_{0}]\) 이외의 값은 단위 임펄스 함수와 곱해지면 모두 0이 되어 버리기 때문에 단위 임펄스 함수의 형태로 나타나 집니다. 예를 들어 \(x[n]\delta[n - (-4)] = x[4]\delta[n - (-4)]\)가 됩니다.

• 이번에는 연속 시간에서의 임펄스 함수와 단위 계단 함수에 대하여 알아보도록 하겠습니다.
• 먼저 임펄스 함수는 다음과 같은 식을 가집니다.

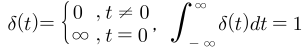
• 이산 시간 케이스와 다르게 \(t = 0\) 지점에서의 값은 무한대를 가지고 전체 범위에서 적분을 하였을 때, 면적의 넓이가 1이 되도록 위 식을 따릅니다.

• 반면 계단 함수의 경우 \(t > 0\) 인 경우에는 함수값이 1이 됩니다.

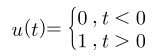
• 이산 시간의 임펄스 함수와 계단 함수는 차분 방정식을 이용하여 두 신호의 관계를 나타내었습니다. 연속 시간에서의 두 함수는 미분 방정식을 이용하여 두 신호의 관계를 나타낼 수 있습니다.

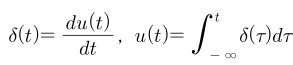
• 이 관계는 이산 시간 신호의 경우와 비교하면서 살펴보면 이해하기 수월합니다. 임펄스 함수는 계단 함수를 \(dt\)로 미분한 관계를 가지고 반대로 계단 함수는 임펄스 함수를 적분한 관계를 가집니다.

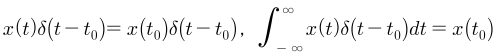
• 위 관계식 또한 임펄스 함수가 특정 시간 이외에는 모든 값이 0이 되는 점을 이용하여 정의되었습니다.
• 연속 시간 신호의 함수를 다른 관점에서 다시 한번 살펴보도록 하겠습니다.

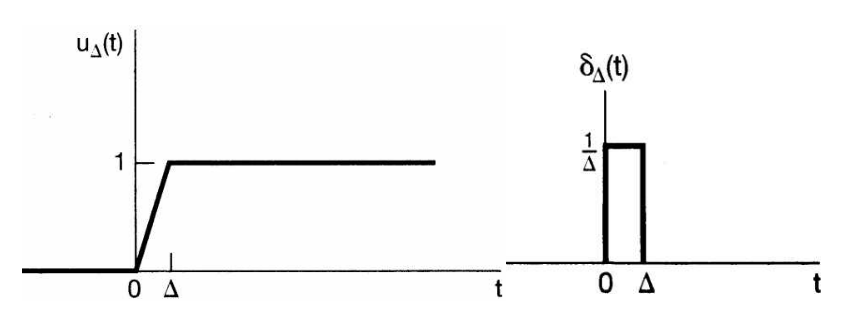
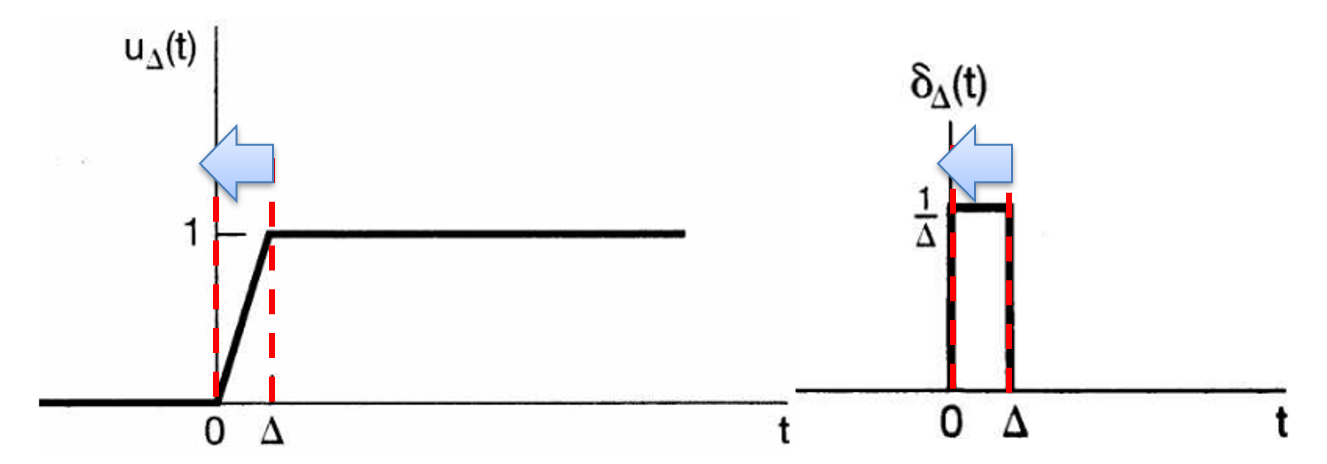
• 왼쪽 그림은 앞에서 살펴본 계단 함수에서 선형적으로 값을 증가하는 부분을 추가한 형태입니다.
• 이와 같은 계단 함수를 임펄스 함수에 대응하면 오른쪽 그림과 같이 나타나게 됩니다. 이 이유를 살펴보도록 하겠습니다.

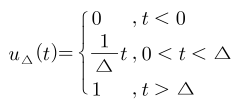
• 앞의 그림의 계단 함수를 구간 별 수식으로 나타내면 위 수식과 같습니다. 계단 함수 → 임펄스 함수로 변환하려면 미분을 이용하여 나타내었습니다. 이번에도 같은 방법으로 계단 함수를 임펄스 함수로 변환해 보도록 하겠습니다. 먼저 \(t < 0\) 때와 \(t > \Delta\)인 경우 상수값이므로 미분을 하면 0이 되고 \(0 < t < \Delta\) 범위의 값 \(\frac{1}{\Delta}t\)를 미분하면 \(\frac{1}{\Delta}\)가 됩니다. 이를 이용하면 임펄스 함수는 다음과 같습니다.

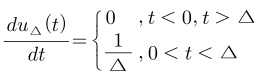
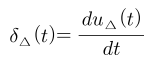
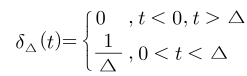
• 앞의 설명에 따라 임펄스 함수 \(\delta_{\Delta}(t)\)는 위 식과 같이 정의할 수 있습니다.

• 이번에는 반대로 임펄스 함수 → 계단 함수로 변환해 보도록 하겠습니다. 이산 시간 케이스에서 다룬 바와 같이 이번에는 적분을 통하여 변환하겠습니다.

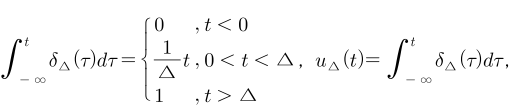
• 이번에 살펴 본 \(\Delta\)를 추가한 계단 및 임펄스 함수에서 \(\Delta\)를 0으로 수렴시키면 어떻게 될까요?

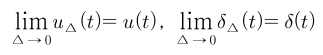
• 위 그림과 수식같이 \(\Delta = 0\)이 되면서 처음 다룬 연속 시간 신호의 임펄스 함수와 계단 함수와 같은 형태로 변경됩니다.

연속 시간 및 이산 시간 시스템

• 앞에서 시스템이란 신호를 처리하는 소프트웨어나 하드웨어를 뜻한다고 설명하였습니다.

• 시스템의 가장 큰 범주로는 연속 시간 시스템 (Continuous Time System)과 이산 시간 시스템 (Discrete Time System)이 존재합니다.
• 그리고 각각의 시스템들을 연결하는 다양한 종류의 연결이 있습니다.

• 위 연결은 직렬 연결이라고 하며 시스템이 연속적으로 연달아 연결되어 있습니다.

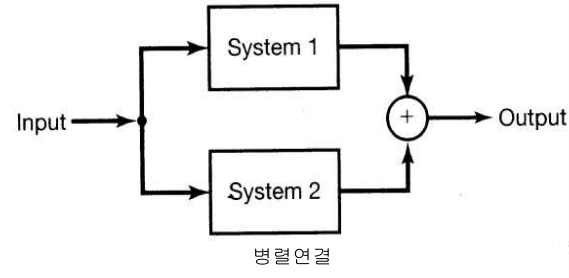
• 위 연결은 병렬 연결 입니다.

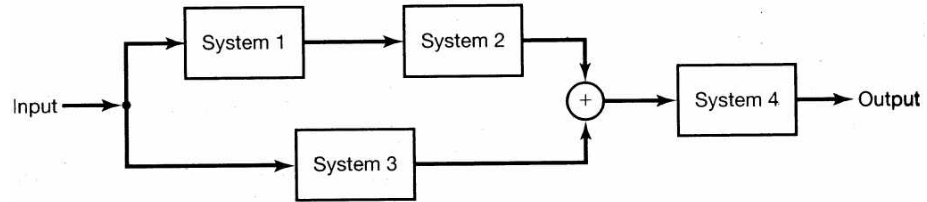
• 위 연결은 직렬과 병렬이 혼합되어 있는 방식입니다.

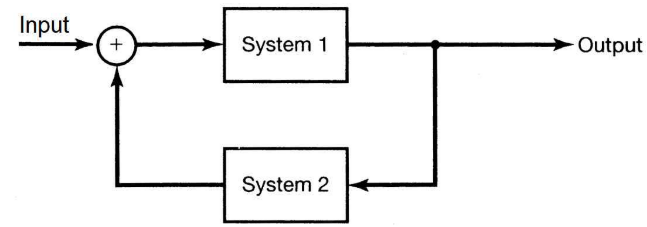
• 위 연결 방식은 피드백 방식으로 출력이 다시 입력으로 연결되는 방식입니다.

기본적인 시스템 특성

• 각 시스템은 연속 및 이산 시간 특성 뿐 아니라 다른 특성들에 의해서 구분되어 지기도 합니다.
• 먼저 메모리 없는 (memoryless)시스템은 어떤 시간의 출력이 동일한 그 시간의 입력에 의해서만 결정되는 시스템을 뜻합니다. 이를 항등 시스템 이라고도 합니다.

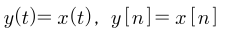
• 반면 메모리가 있는 시스템은 어떤 시간의 출력이 그 시간이나 과거 시간의 입력과 시스템 상태에 의해서 결정되는 시스템을 뜻합니다.

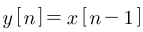
• 예를 들어 위 식과 같은 지연기가 있습니다.

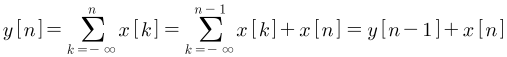
• 또는 위 식과 같은 누산기가 있습니다.

• Signal and System 목차