선형계획법을 이용한 최대 유량 문제와 엑셀의 활용

2021, Apr 30    

• 이전 참조 글 1 : https://gaussian37.github.io/etc-or-linear_programming/
• 이전 참조글 2 : https://gaussian37.github.io/etc-or-transportation_assignment/

• 이번 글에서는 최대 유량 문제를 선형계획법과 엑셀을 활용하여 어떻게 풀 수 있는 지 살펴보도록 하겠습니다. 포드 풀커슨같은 알고리즘을 이용하여 최대 유량 문제의 풀이 방법을 알고 싶으시면 아래 링크를 참조하시기 바랍니다.
  • 링크 : https://gaussian37.github.io/math-algorithm-network_flow

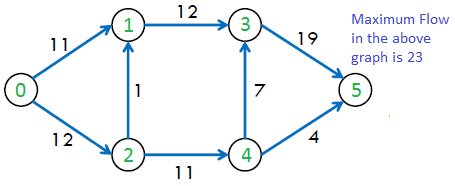
최대 유량 기본 예제

• 최대 유량 기본 문제 엑셀 시트 : https://drive.google.com/file/d/1FHLfIlwR2A0pQays8C0UbY27hJQg8AqP/view?usp=sharing

• 먼저 최대 유량 문제에는 그래프가 주어 지고 그래프의 노드와 노드를 연결하는 간선에 최대로 이동할 수 있는 양이 주어집니다.

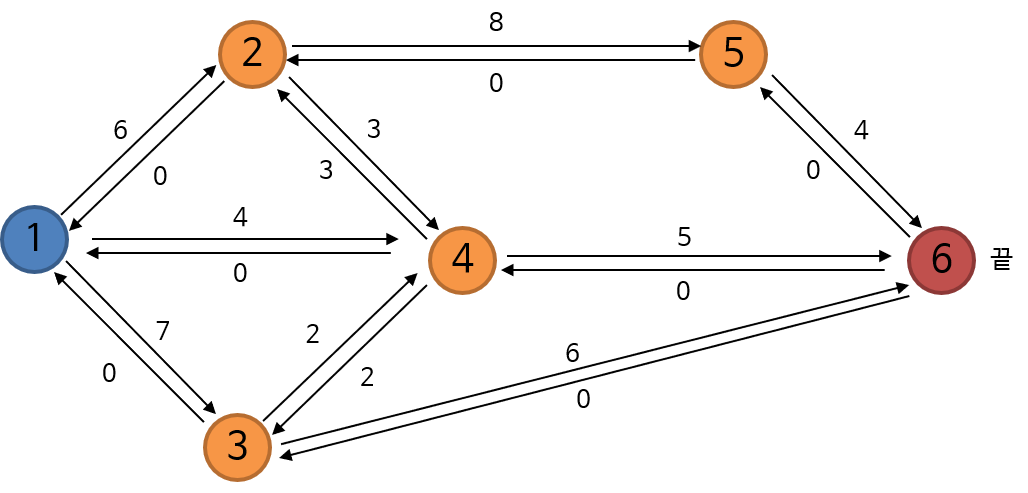
• 위 그래프에서 각 동그라미에 해당하는 노드를 연결하는 간선에는 최대로 이동시킬 수 있는 양이 정해져 있습니다.
• 예를 들어 1 → 2로 한번에 이동할 수 있는 최대 양은 6입니다.
• 이와 같이 각 간선마다 최대 용량이 정해져 있는 그래프에서 파란색 동그라미는 출발점, 빨간색 동그라미는 도착점일 때, 출발점에서 도착점까지 전달할 수 있는 최대 용량을 구하는 문제를 최대 용량 문제라고 말합니다.
• 이 문제를 선형 계획법을 이용하여 풀 수 있으며 위 그래프를 기준으로 제약식을 만들어 보도록 하겠습니다.

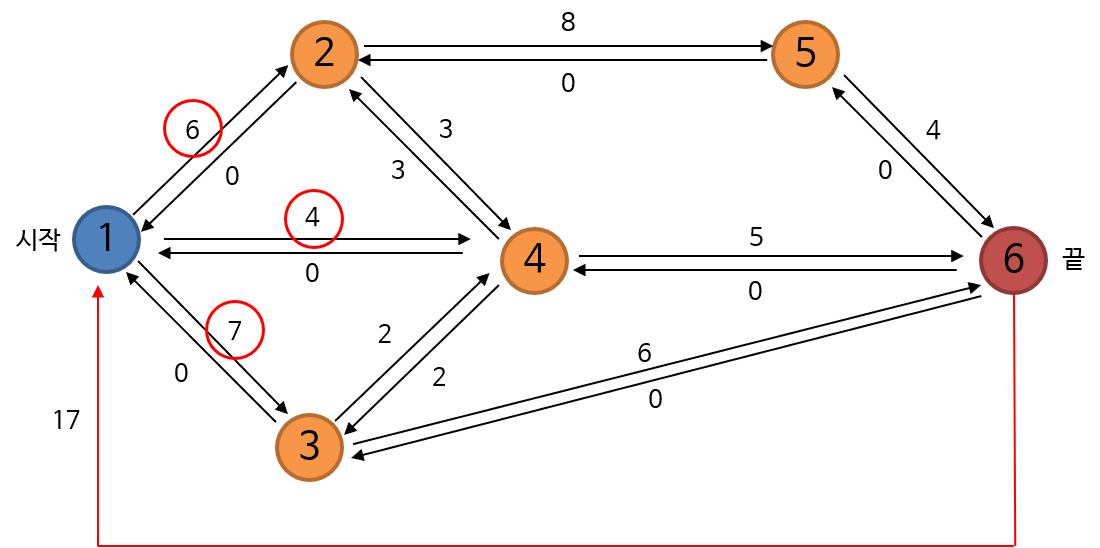
• 이 때, 제약 조건을 추가하기 위해 위 그래프와 같이 도착점 → 시작점으로 잇는 간선을 추가하며 그 간선의 용량을 시작점에서 보낼 수 있는 용량의 총합으로 설정합니다.
• 위 그래프를 보면 6 + 4 + 7 = 17이 됨을 알 수 있습니다.
• 이와 같이 제약 조건을 추가하는 이유는 시작점에서 보낼 수 있는 도착 지점의 최대 용량이 시작점에서 보낼 수 있는 용량의 합보다 커지는 것을 방지하기 위함입니다.

• ① 의사 결정 변수 :
  • 　$X_{ij}$ : $i$ ~ $j$ 간선 사이의 유량
• ② 목적 함수 :
  • 최대화 : $Z = X_{61}$
• ③ 제약 조건 :
  • 　$X_{61} - X_{12} - X_{13} - X_{14} = 0$
  • 　$X_{12} + X_{42} - X_{24} - X_{25} = 0$
  • 　$X_{13} - X_{34} - X_{36} = 0$
  • 　$X_{14} + X_{24} + X_{34} - X_{42} - X_{43} - X_{46} = 0$
  • 　$X_{25} - X_{56} = 0$
  • 　$X_{36} + X_{46} + X_{56} - X_{61} = 0$
  • 　$X_{12} \le 6$
  • 　$X_{13} \le 7$
  • 　$X_{14} \le 4$
  • 　$X_{24} \le 3$
  • 　$X_{25} \le 8$
  • 　$X_{34} \le 2$
  • 　$X_{36} \le 6$
  • 　$X_{42} \le 3$
  • 　$X_{43} \le 2$
  • 　$X_{46} \le 5$
  • 　$X_{56} \le 5$
  • 　$X_{61} \le 17$
  • 　$X_{ij} \ge 0$
  • 　$X_{ij} = \text{integer}$

• 먼저 위 조건들을 하나씩 살펴보겠습니다.
• 의사 결정 변수는 최대 용량을 사용하기 위하여 각 간선에서 실제 사용하는 용량을 나타냅니다.
• 목적 함수는 도착점 → 출발점 으로 다시 전달하는 용량을 최대화 하는 것입니다. 즉, 도착점에서 수용 가능한 최대 용량과 동일한 의미를 가집니다. 다만 간선으로 표현하기 위해 이와 같은 트릭을 사용하는 것입니다.
• 제약 조건의 기본 컨셉은 유입량 = 유출량입니다. 각 노드 기준으로 유입된 양만큼 유출해야 하기 때문입니다. 각 노드 기준으로 유입양은 +로 유출양은 -로 나타내어 총 합이 0이 되도록 제약 조건을 걸어줍니다.
• 추가적인 제약 조건으로 각 간선 별 최대 용량에 대한 제한을 합니다.
• 마지막으로 도착점 → 출발점으로 보낼 수 있는 최대 용량을 출발점에서 유출할 수 있는 총 양의 합으로 제한을 걸어 줍니다.
• 위 와같이 의사 결정 변수, 목적 함수, 제약 조건을 이용하여 선형 계획법을 풀면 목적 함수에서 최대 용량을 찾을 수 있습니다. 의미를 차근 차근 생각해 보면 크게 어렵지 않습니다.

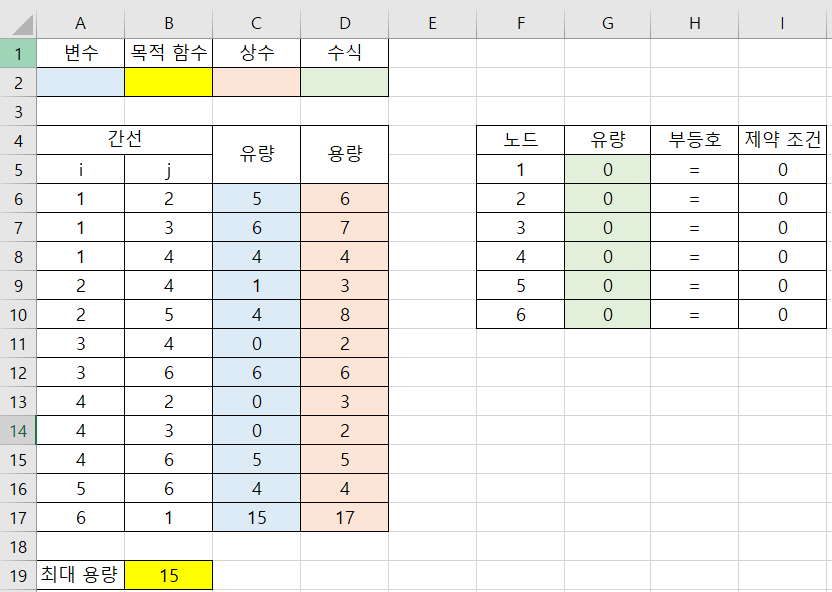
• 엑셀을 이용하면 위 표와 같이 풀 수 있습니다.

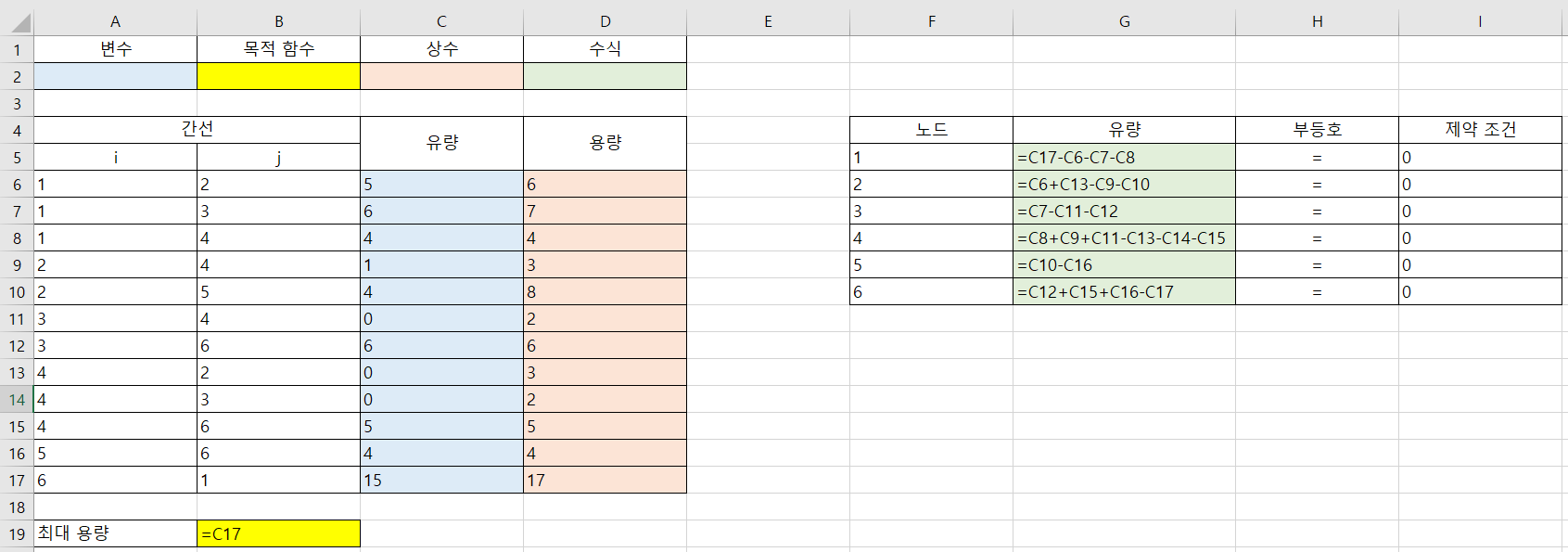
• 수식을 상세히 보면 위 표와 같습니다.

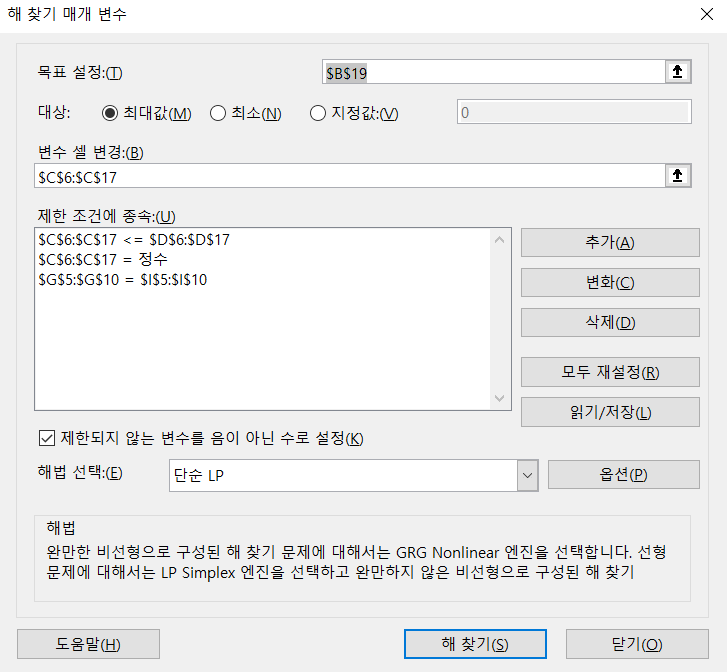
• 위 절차를 통하여 최대 유량은 15로 구할 수 있으며 최대 유량이 선택 되기 위한 각 간선의 유량을 구할 수 있습니다.