선형계획법을 이용한 최단 경로 문제와 엑셀의 활용

2021, Apr 29    

• 사전 필요 지식 : https://gaussian37.github.io/etc-or-linear_programming/

• 선형계획법을 이용하여 그래프의 최단 경로 문제를 해결할 수 있습니다.
• 물론 최단 경로 문제를 해결하기 위한 효율적인 알고리즘들이 있습니다. 컴퓨터 알고리즘에서 다루는 다익스트라 알고리즘을 사용하는 것이 더 효율적일 수 있습니다.
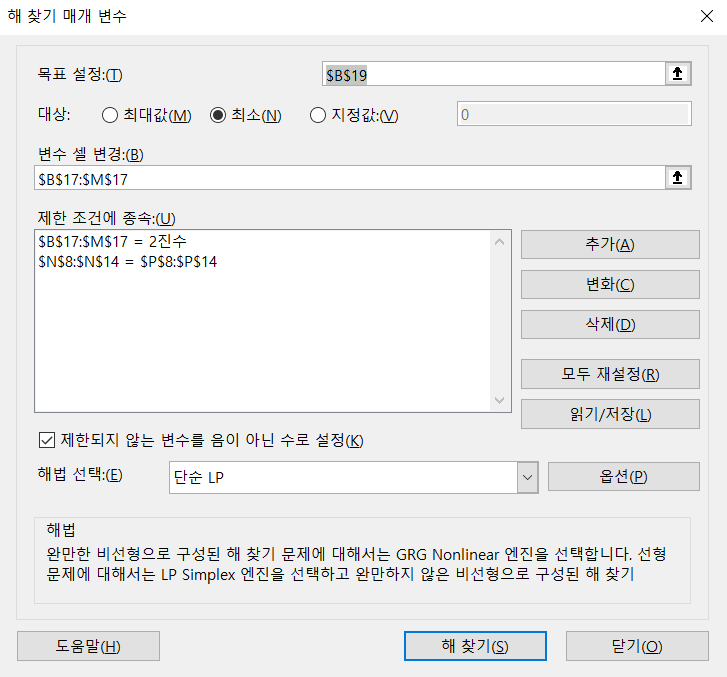
• 이번 글에서는 선형 계획법을 이용하여 그래프의 최단 경로 문제를 해결하는 방법을 배우고 엑셀을 이용하여 해를 찾아보겠습니다.

• 최단 경로 문제 엑셀 시트 : https://drive.google.com/file/d/12p2tTqP4rjDZf7galYMstjcYOo7yOrFs/view?usp=sharing

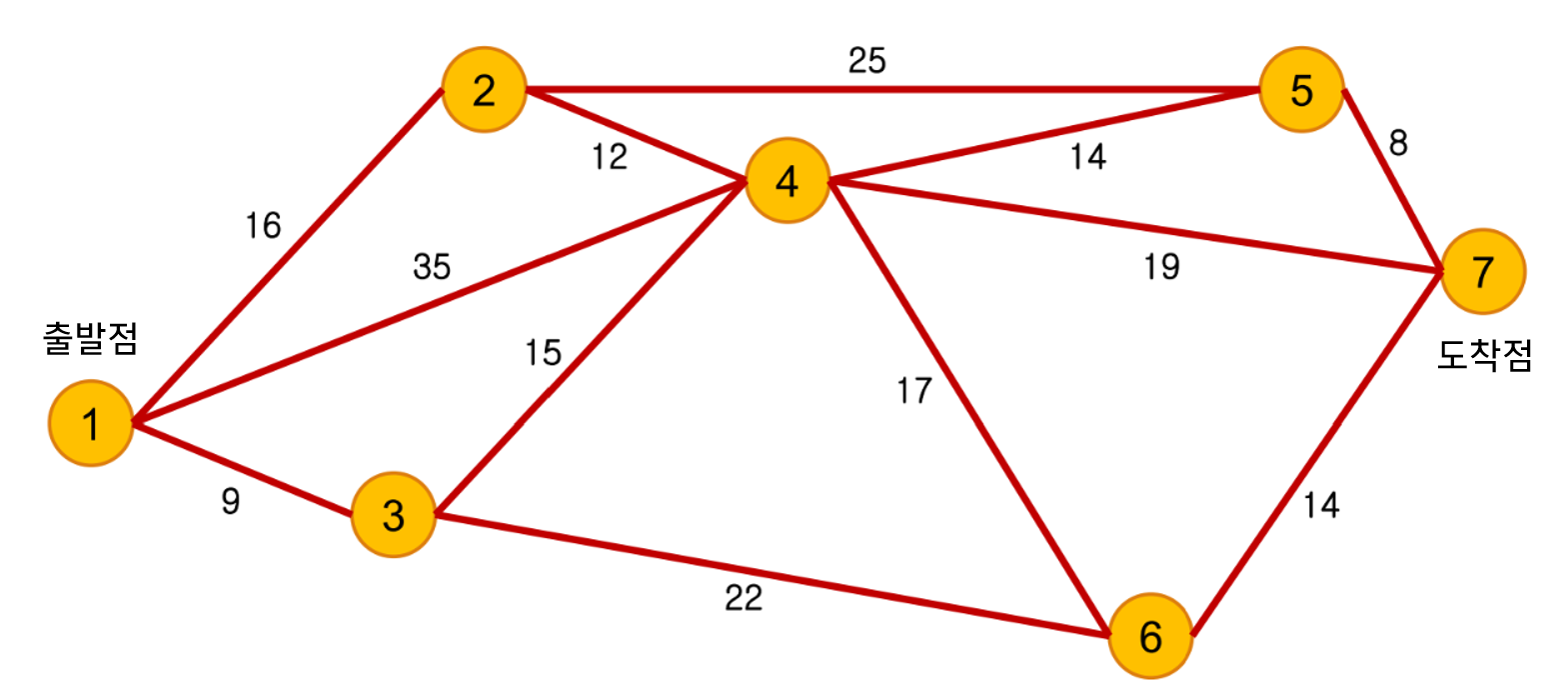
• 위 그림과 같은 그래프가 있다고 가정해 보겠습니다. 1번이 출발점이고 7번이 도착점 입니다.
• 최단 경로 문제에서는 의사결정 변수로 간선을 기준으로 만들어야 합니다.

• 의사 결정 변수 : 간선 i와 j가 최단 경로에 포함되면 1, 포함되지 않으면 0

• 목적 함수는 의사 결정 변수로 정의된 간선과 각 간선의 비용을 이용하여 선택된 간선의 총합이 최소가 되도록 만들어야 합니다.

• 제약식을 두는 방식에서는 노드 관점에서 2가지 기준을 둡니다.
  • ① 출발 및 도착 지점의 노드로 들어오는 간선은 1개가 선택되어야 한다. 예를 들어 \(x_{12} + x_{13} + x_{14} = 1\)을 만족하도록 설정해야 합니다.
  • ② 출발 및 도착 지점의 노드 이외에는 유입량 - 유출량 = 0을 만족해야 한다. 예를 들어 \(x_{12} - x_{24} - x_{25} = 0\)을 만족하도록 설정해야 합니다.

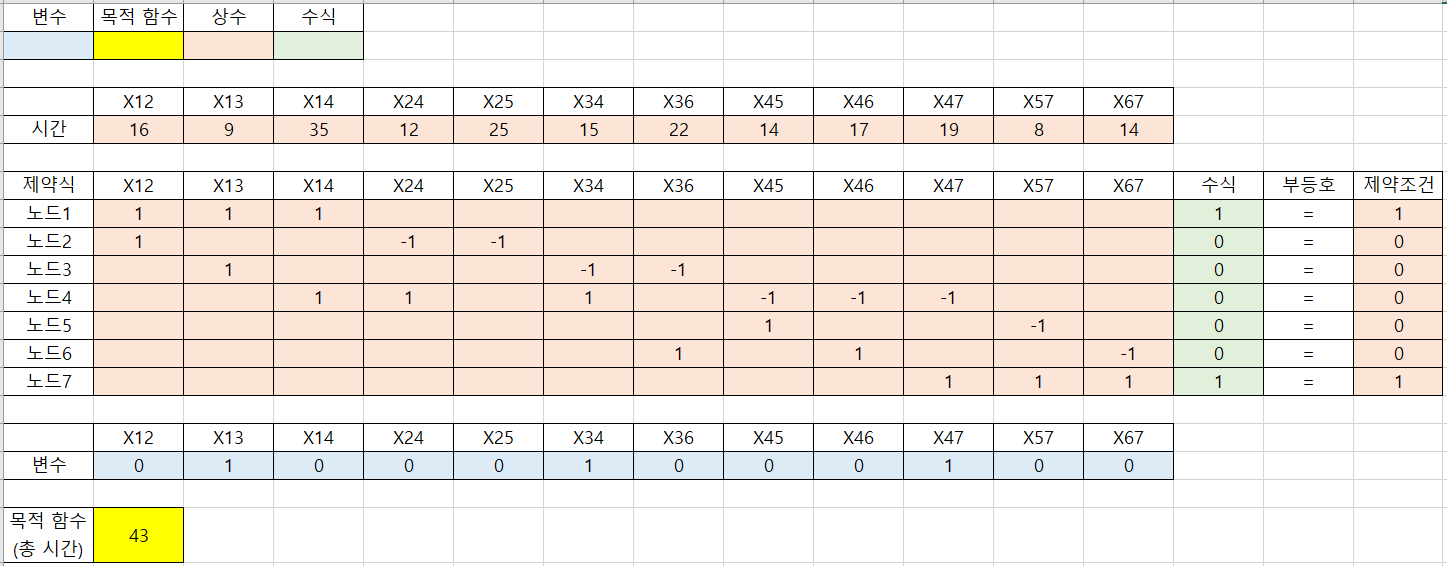
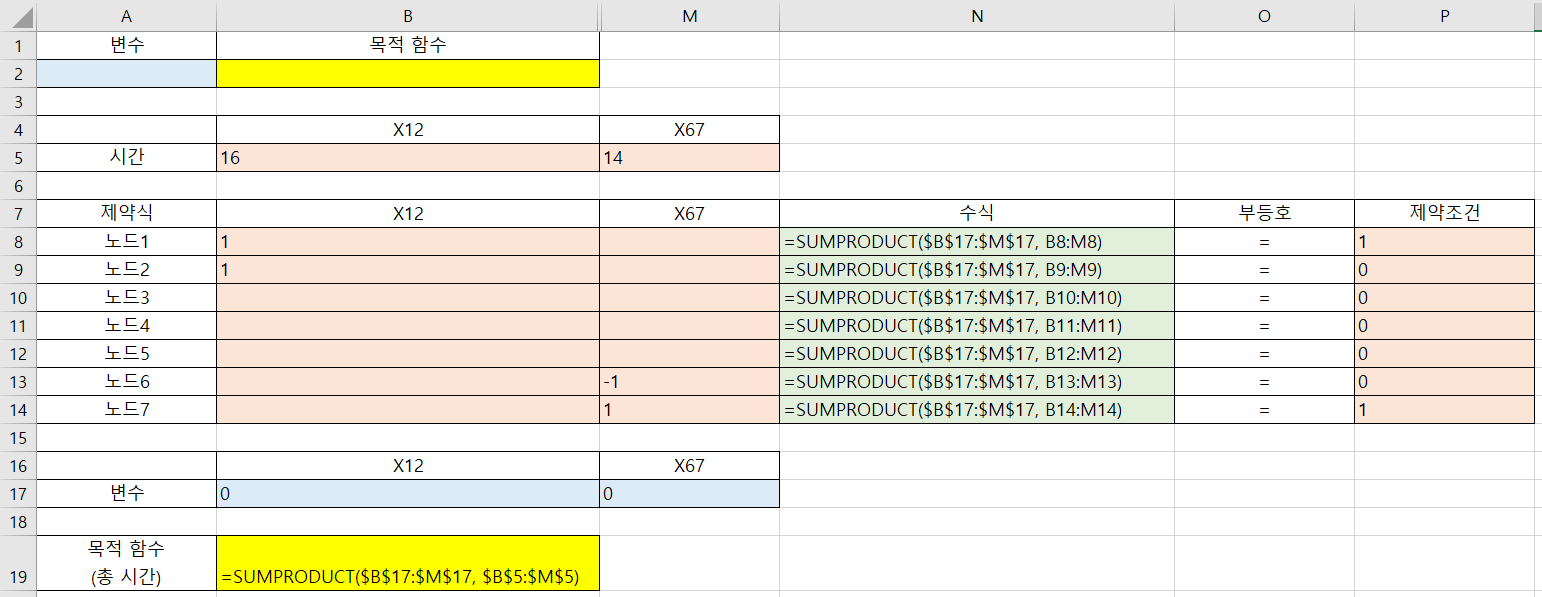
• 앞의 개념을 이용하여 전체적 조건을 정리하면 다음과 같습니다.
• 의사 결정 변수 : 간선 i와 j가 최단 경로에 포함되면 1, 포함되지 않으면 0
• 목적 함수 : \(\text{Minimize } Z = 16x_{12} + 9x_{13} + 35x_{14} + 12x_{24} + 25x_{25} + 15x_{34} + 22x_{36} + 14x_{45} + 17x_{46} + 19x_{47} + 8x_{57} + 14x_{67}\)
• 제약식 :
  • ① 노드 1 (출발점) : \(x_{12} + x_{13} + x_{14} = 1\)
  • ② 노드 2 : \(x_{12} - x_{24} - x_{25} = 0\)
  • ③ 노드 3 : \(x_{13} - x_{34} - x_{36} = 0\)
  • ④ 노드 4 : \(x_{14} + x_{24} + x_{34} - x_{45} - x_{46} - x_{47} = 0\)
  • ⑤ 노드 5 : \(x_{25} + x_{45} - x_{57} = 0\)
  • ⑥ 노드 6 : \(x_{36} + x_{46}- x_{67} = 0\)
  • ⑦ 노드 7 (도착점) : \(x_{47} + x_{57} + x_{67} = 1\)