선형계획법을 이용한 수송 및 할당 모형과 엑셀의 활용
2021, Apr 29
- Operational Research의 주요한 문제로
수송 문제와할당 문제가 있습니다. 수송 문제와 할당 문제는 의사 결정 시 굉장히 중요한 문제이므로 Operational Research에서도 중요한 문제로 다루어 집니다. 이번 글에서는 간단한 선형계획법 방식을 이용하여 엑셀로 이 문제를 해결 하는 방법에 대하여 다루어 보겠습니다. - 선형계획법으로 이 문제를 푸는 데에는 다소 효율적이지 못하지만 간단하게 풀 수 있으므로 입력 값의 갯수가 많지 않다면 유효하게 사용할 수 있습니다.
선형계획법을 이용한 수송 문제
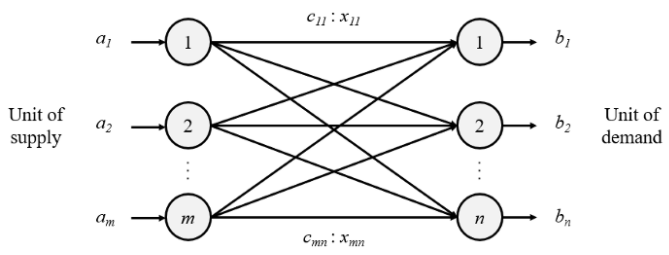
수송 문제는 N개의 출발점과 M개의 도착점이 있고, 각 출발점에서 각 도착점 까지 물건을 이동하는 데 발생하는 비용과 이동 해야할 물량이 정해집니다. 이 때, 이익을 최대화 하거나 수송 비용을 최소화하는 문제에 해당합니다.수송 문제network flow라고 알려진 더 큰 범주의선형계획법에 속하여 매우 효율적이고 독특한 수리적인 해법(심플렉스법의 변형)을 통해 해결 할 수 있습니다. 물론 이 글에서는 엑셀을 이용한 선형 계획법을 이용하여 문제를 해결할 예정입니다.- 대표적인
수송 문제의 조건은 다음과 같습니다.전제 조건: 공급원의 제품 공급 능력과 수요지의 수요량을 알고 있어야 합니다.문제: 다수의 공급원에서 다수의 수요지로 제품을 운송해야 하며 가능한 수송경로 별 수송량을 결정해야 합니다.목적: 이익을 최대화 하거나 수송비를 최소화 합니다.사용 분야: 최적의 수송량 결정, 새로운 입지 결정, 다수의 후보 평가 등에 사용됩니다.
- 다시 정리하면
수송 문제는 최소의 비용으로 제품을 다수의 출발지로부터 다수의 도착지 까지 수송하는 문제입니다. 각 출발지는 고정된 양만큼의 제품을 공급할 수 있고, 각 도착지는 고정된 수요량을 가집니다. - 선형 모형은 각 출발지의 공급량에 대한 제약식과 각 도착지의 수요량에 대한 제약식을 가집니다. 총 수요량과 총 공급량이 일치할 경우, 제약식들은
등식으로 표현될 수 있습니다. 반면 총 수요량과 총 공급량이 불일치할 경우, 제약식들은부등식으로 표현될 수 있습니다. - 구체적인 예제를 통하여 수송 문제를 풀어보도록 하겠습니다.
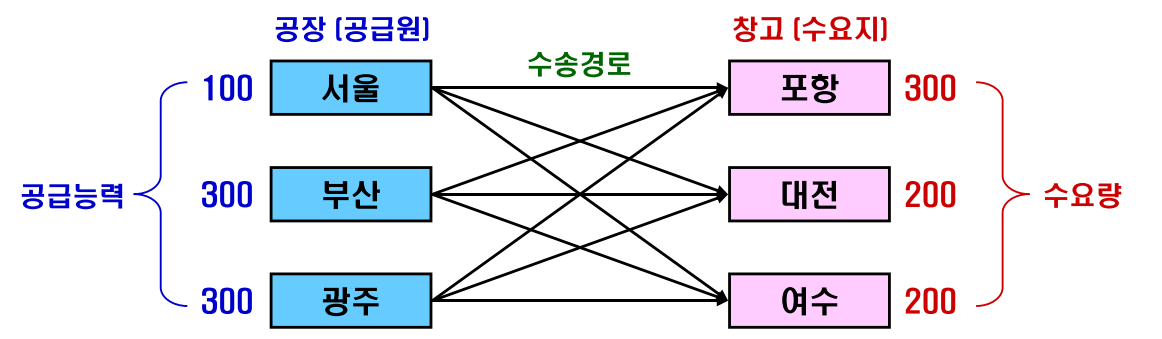
- 위 그래프와 같이 왼쪽이 공급에 해당하고 오른쪽이 수요에 해당하며 각 공급지의 공급 능력과 수요지의 수요량이 정해져 있다고 가정하겠습니다.
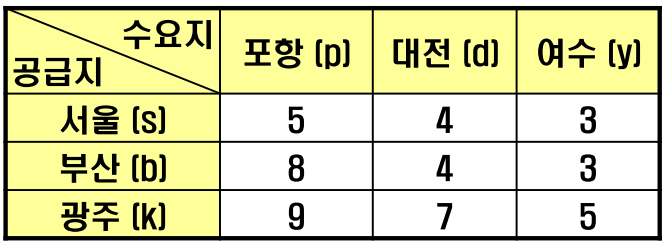
- 이 때, 각 공급지에서 수요지로 수송 시 수송비가 위 도표와 같이 주어집니다.
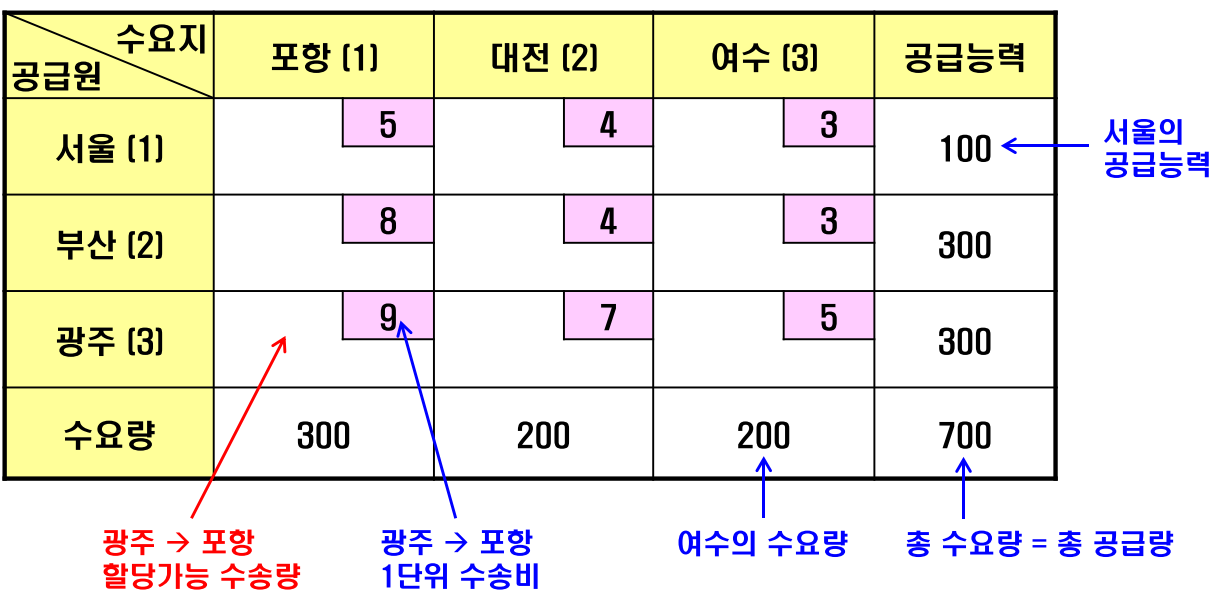
- 일반적으로
수송 문제에서는 위 표와 같이 수요량, 공급량 및 수송 비용을 하나의 도표에 표현합니다. - 위 정보들을 이용하여 문제를 정리해 보겠습니다.
- ①
의사 결정 변수:- \(X_{ij}, (i=1,2,3, j=1,2,3)\) : 공급원 \(i\)에서 수요지 \(j\) 까지의 수송량
- ②
목적 함수:- 최소화 : \(Z = \sum_{i=1}^{m}\sum_{j=1}^{n} C_{ij}X_{ij}\)
- ③
제약 조건:- \(\sum_{j=1}^{n} X_{ij} = S_{i}, \ \ i = 1, 2, \cdots , m\)
- \(S_{i}\) : 공급지 \(i\)의 공급 능력
- \(\sum_{i=1}^{m} X_{ij} = D_{j}, \ \ j = 1, 2, \cdots, n\)
- \(D_{j}\) : 수요지 \(j\)의 수요량
- \(X_{ij} \ge 0, \ \ i=1,2,3 \ \ j=1,2,3\)
- \(\sum_{j=1}^{n} X_{ij} = S_{i}, \ \ i = 1, 2, \cdots , m\)
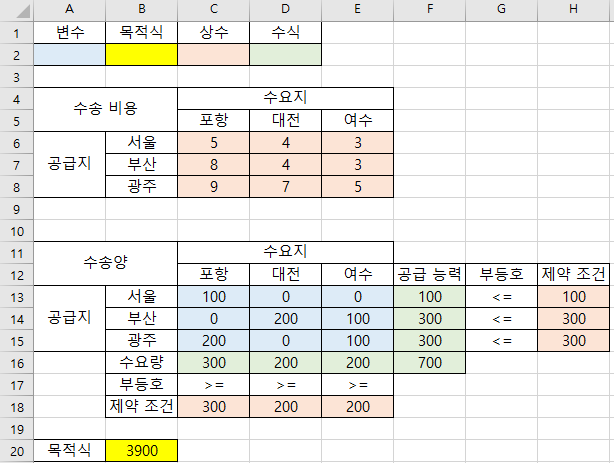
- 앞에서 정의한 수식을 엑셀에 표현하면 위 그림과 같이 나타낼 수 있습니다.
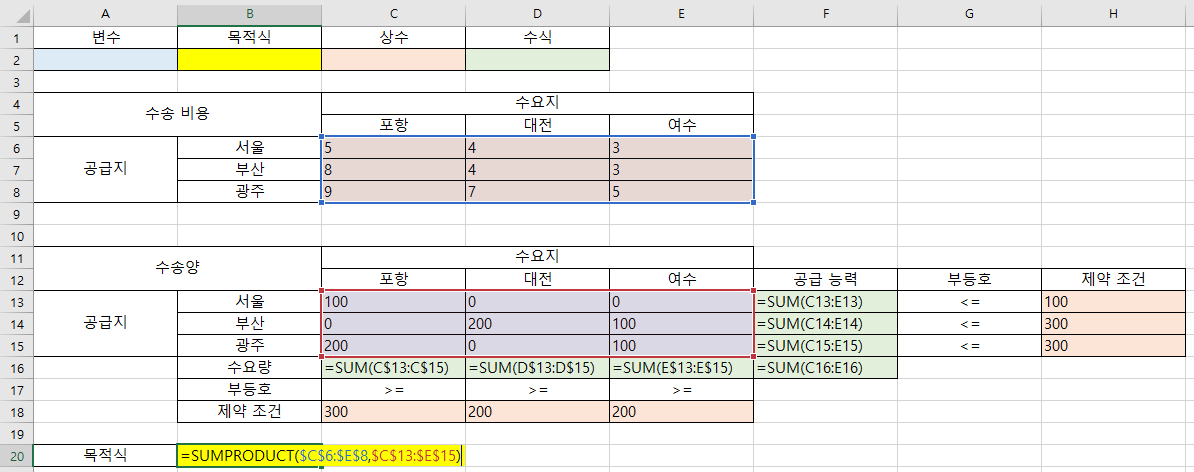
- 앞에서 정의한 수식을 하나 씩 살펴보면 목적 함수와 제약 조건을 살펴볼 수 있습니다.
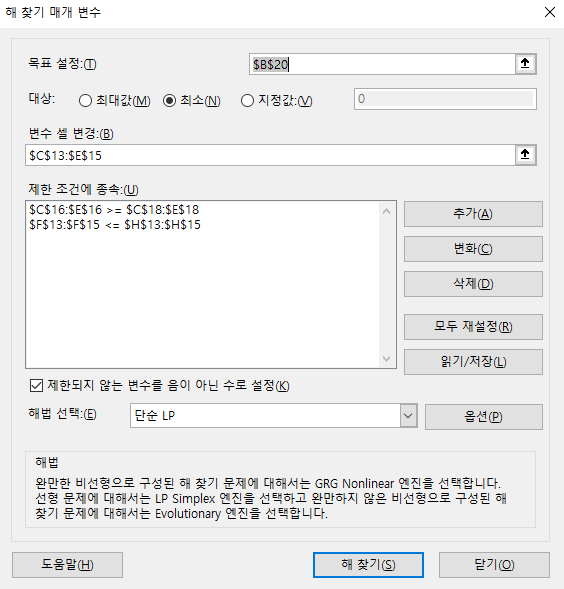
- 해 찾기를 통해 위 식의 제약 조건을 적용하였고 그 결과 3900이라는 최소 비용을 구할 수 있습니다.
선형계획법을 이용한 할당 문제
할당 문제는 N명의 작업자와 M개의 작업이 있을 때, 작업자와 작업을 매칭하는 문제를 말합니다. 각 작업자는 1개의 작업만 할 수 있고 각 작업은 한 명의 작업자에 의해 선택될 수 있습니다. 이 때, 이익을 최대화 하거나 비용을 최소화 하는 문제가 할당 문제에 해당합니다.할당 문제또한 선형 계획법 이외의 방법으로 더 효율적으로 풀어낼 수 있습니다. 이 글에서는 쉽게 접근할 수 있는 선형 계획법을 이용하여 문제를 풀 예정이고 할당 문제에 관심이 있으면헝가리안 알고리즘을 꼭 공부해 보시길 추천 드립니다.- 대표적인
할당 문제의 조건은 다음과 같습니다.전제 조건: 작업자의 수 (공급량)과 작업의 수 (수요량)을 알고 있어야 합니다.문제: 다수의 과제에 대수의 사람을 할당하며, 한 개의 과제에 한 명의 사람만 할당 할 수 있습니다.목적: 할당 이익을 최대화 하거나 할당 비용을 최소화 합니다.사용 분야: 과제에 인적 자원을 할당, 판매원에게 담당 지역을 할당, 기계에 작업을 할당 등이 있습니다.
- 할당 문제를 가장 쉽게 접근하는 방법은 단순 열거 법으로 모든 경우의 수를 다 나열해서 풀 수 있습니다. 다만, 이 경우 문제의 복잡도가
팩토리얼로 늘어나기 때문에 굉장히 비효율적입니다. - 이번 글에서는 선형 계획법을 이용하여 할당 문제를 풀어보겠습니다. 이 방법은 앞에서 다룬
수송 문제와 크게 다르지 않으며 제약 조건에서 일부 차이가 있습니다.
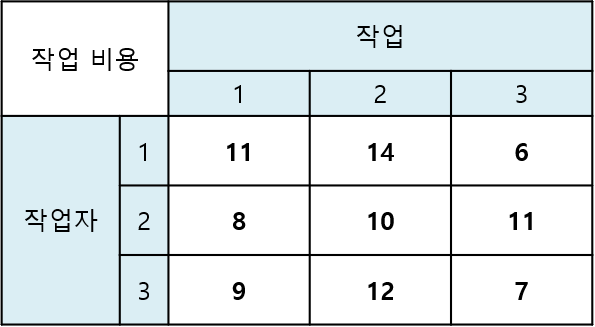
- 위 표와 같이 3명의 작업자와 3개의 작업이 있고 각 작업자 별 작업에 해당하는 비용이 있습니다.
- 앞의 수송 문제와 비교하였을 때 공통점은 비용을 최소화 한다는 점이고 차이점은 제약 조건에 있습니다.
- 할당 문제에서의 제약 조건은 각 작업자 별 선택된 작업 수의 합이 1이 되어야 하고 동시에 작업 측면에서도 모든 작업자들 중 한 명에게 선택되어야 합니다.
- 위 정보들을 이용하여 문제를 정리해 보겠습니다.
- ①
의사 결정 변수:- \(X_{ij}, (i=1,2,3, j=1,2,3)\) : 작업자 \(i\)가 작업 \(j\)를 선택한 유무 (0, 1)
- ②
목적 함수:- 최소화 : \(Z = \sum_{i=1}^{m}\sum_{j=1}^{n} C_{ij}X_{ij}\)
- ③
제약 조건:- \(\sum_{j=1}^{n} X_{ij} = 1, \ \ i = 1, 2, \cdots , m\)
- \(\sum_{i=1}^{m} X_{ij} = 1, \ \ j = 1, 2, \cdots, n\)
- \(X_{ij} \ge 0, X_{ij} = binary \ \ i=1,2,3 \ \ j=1,2,3\)
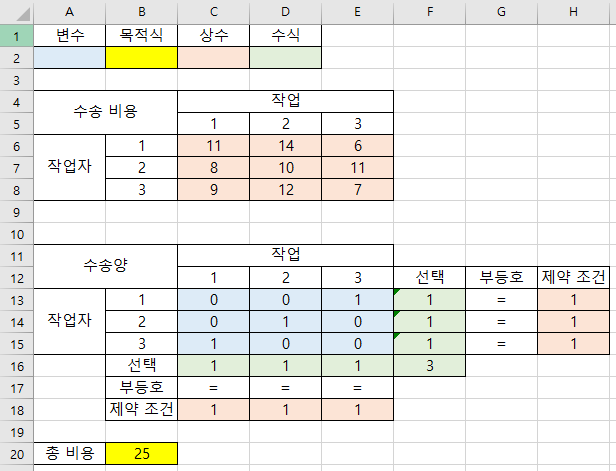
- 앞에서 정의한 수식을 엑셀에 표현하면 위 그림과 같이 나타낼 수 있습니다.
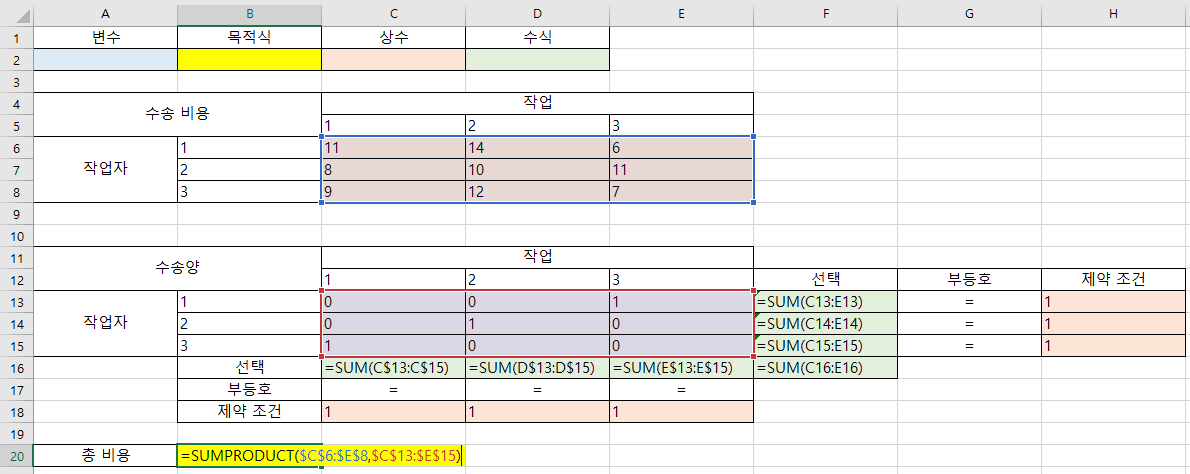
- 앞에서 정의한 수식을 하나 씩 살펴보면 목적 함수와 제약 조건을 살펴볼 수 있습니다.
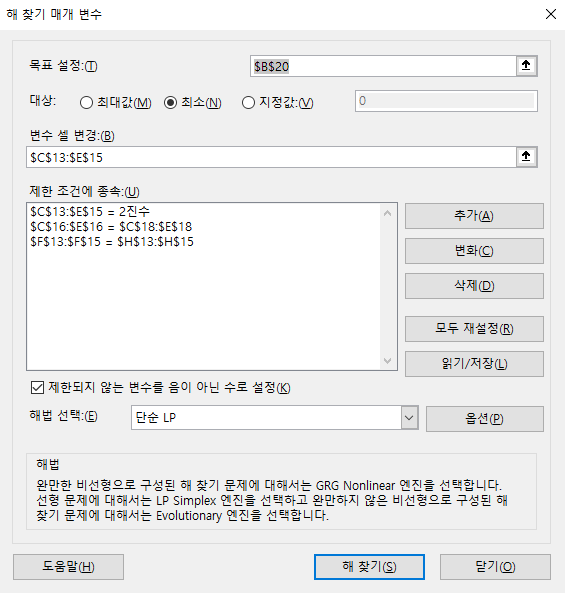
- 해 찾기를 통해 위 식의 제약 조건을 적용하였고 그 결과 25라는 최소 비용을 구할 수 있습니다. 이 때, 작업자와 작업이 매칭된 결과를 보면 한 명의 작업자가 하나의 작업에 매칭이 된 것을 확인할 수 있습니다.