선형 부분공간

출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)

이번 시간에는 선형 부분공간(linear subspace)에 대하여 알아보도록 하겠습니다.

$1$

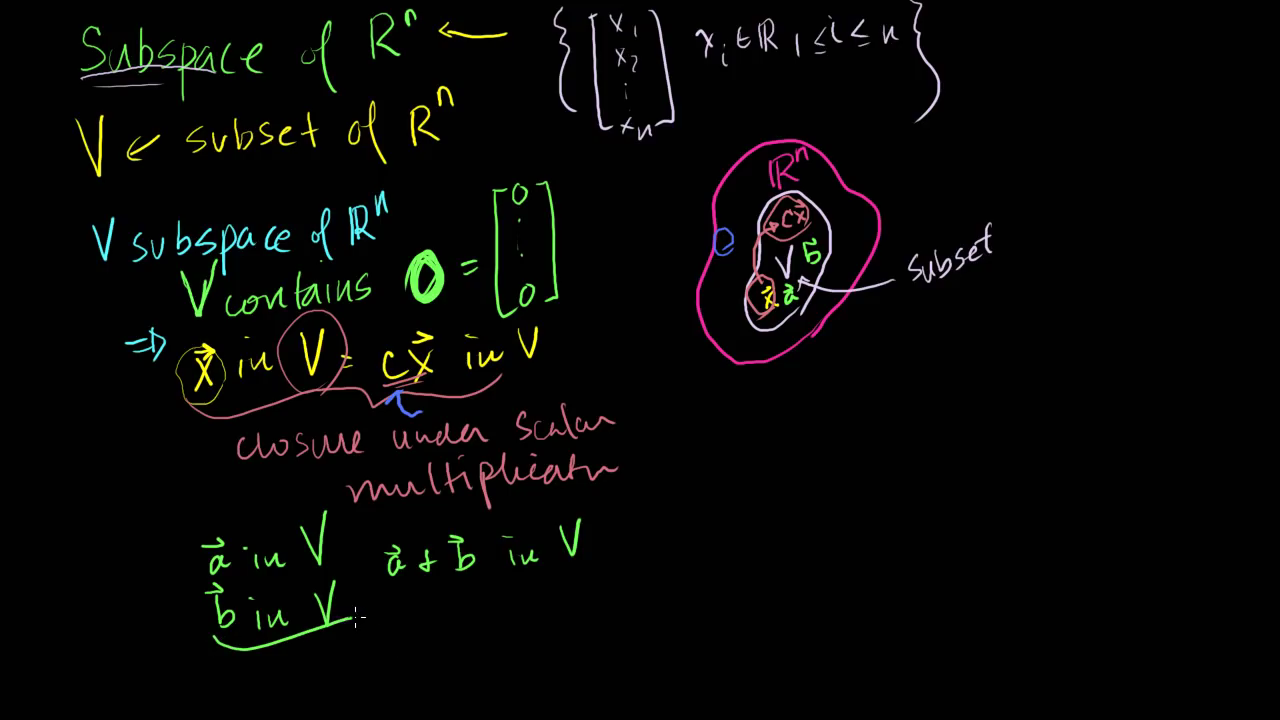
$\mathbb{R}^{n}$ 은 n차원의 실수 전체 공간을 뜻합니다.
$\mathbb{R}^{n}$ 안에는 subset(부분집합) V가 있다고 가정합니다.
- subset V = $\{ [ x_{1}, x_{2}, ... , x_{n} ] , x_{i} \in \mathbb{R}, 1 \le i \le n \}$
subset V는 다음 3가지 성질을 만족하면 subspace(부분공간) 의 조건을 만족할 수 있습니다.
- 덧셈 연산에 닫혀 있을 것
- 스칼라곱 연산에 닫혀 있을 것
- 0 벡터를 포함할 것
$\vec{x}$ 가 V안에 속하는 벡터라면 $\vec{x}$ 에 어떤 상수배를 하여 $c\vec{x}$ 를 하더라도 V안에 속해야 subspace 라고 할 수 있습니다.
- 즉, subspace 내에서는 스칼라 곱에 대한 연산이 닫혀 있습니다.
또한 V 안의 어떤 벡터들을 더한다고 하더라도 V안에 속해야 subspace 라고 할 수 있습니다.
- 즉, subspace 내에서는 덧셈 연산에 대하여 닫혀 있습니다.

$2$

$3$

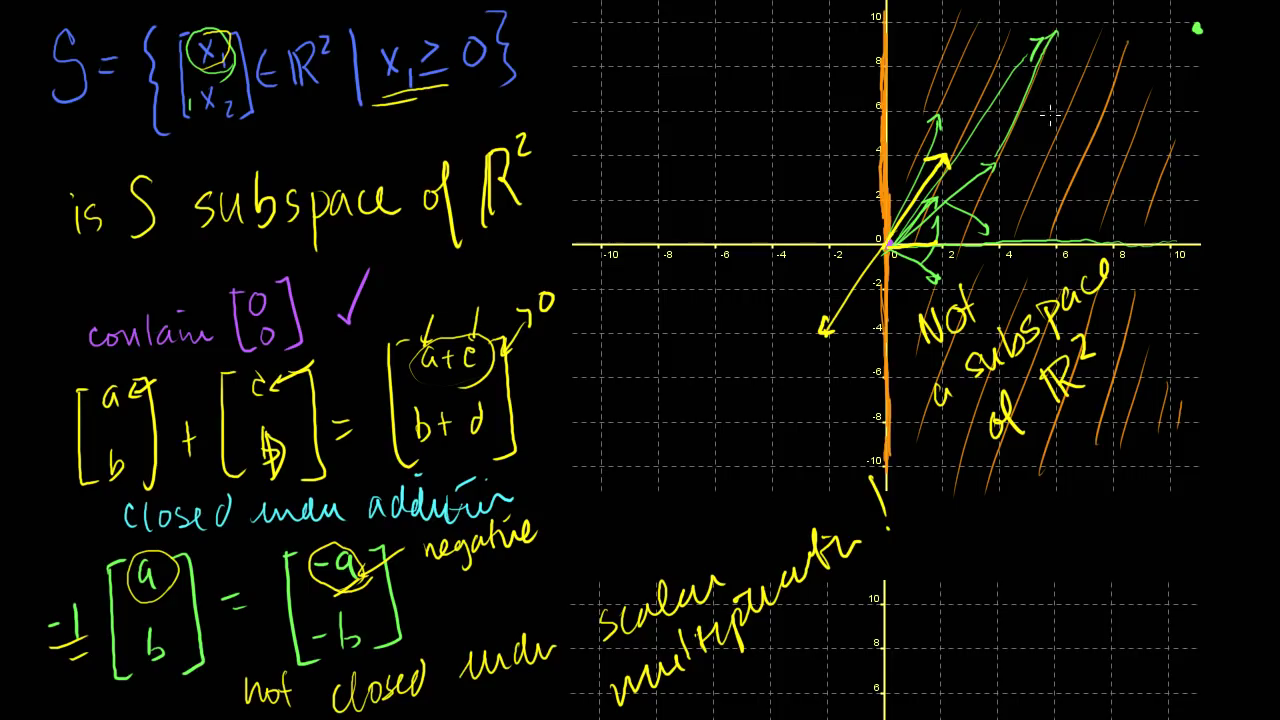
위 예제에서는 subset에 조건이 걸려 있습니다. $x_{1} \ge 0$ 이란 조건이 추가 되었습니다.
이 때에는 앞의 예제 처럼 모든 벡터에 대하여 덧셈과 스칼라곱이 닫혀 있지 않습니다.
예를 들어 초록색 식처럼 -1을 곱하게 되면 subset이 subspace 조건을 벗어나게 됩니다. 이 때에는 닫혀 있지 않다고 합니다.

$4$

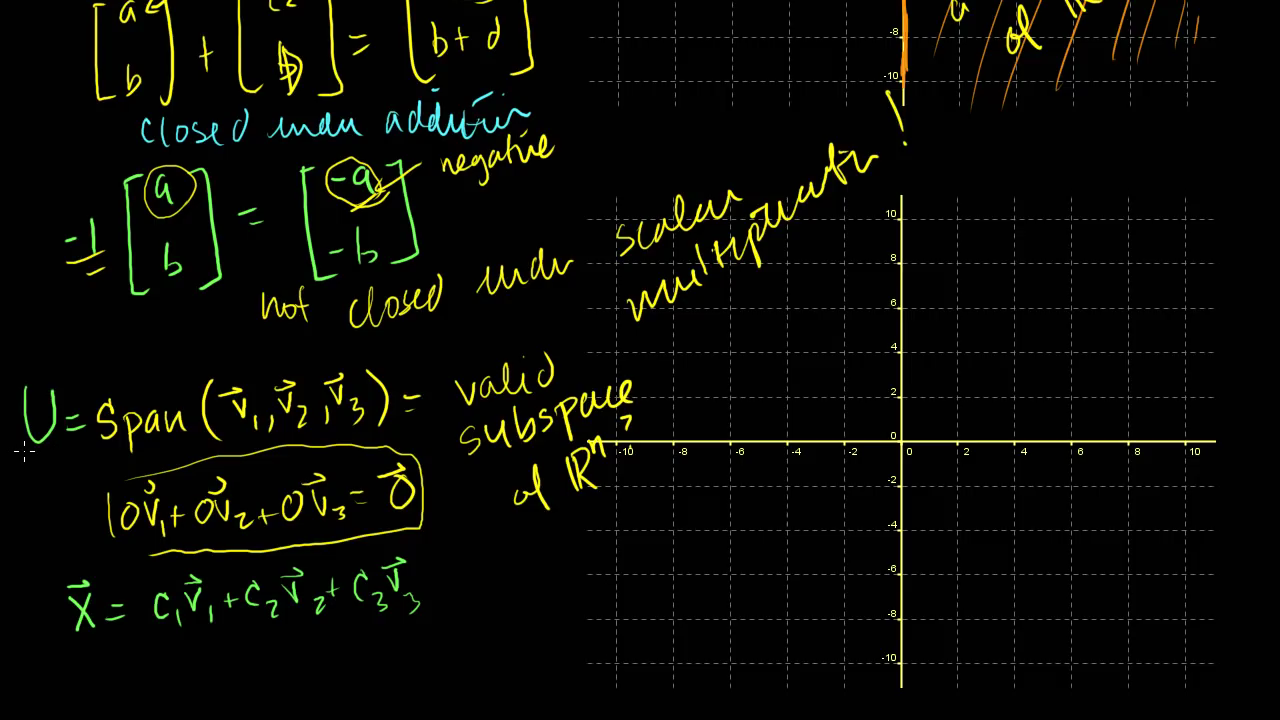
어떤 집합의 선형생성을 알고 싶다면, span 형태로 정의할 수 있습니다.
- 위의 예제처럼 $Span(\vec{1}, \vec{2}, \vec{3})$ subspace를 정의해 볼 수 있습니다.

$5$

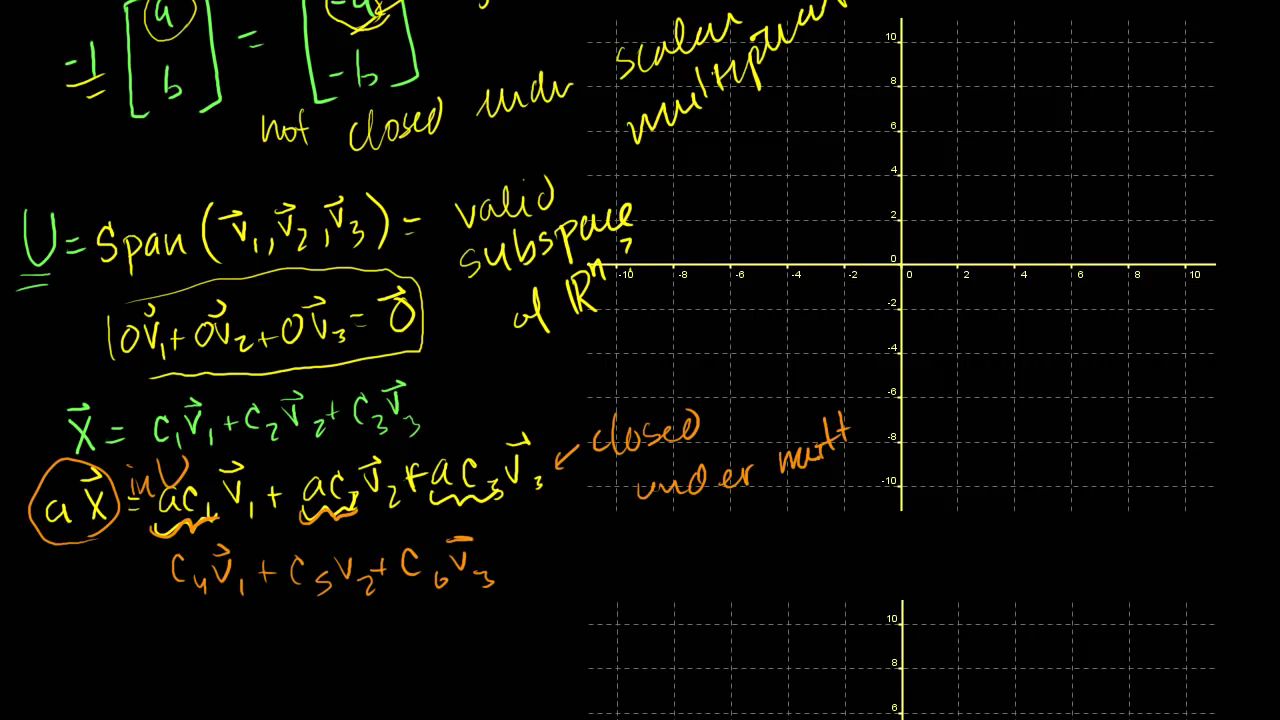
스칼라 곱이 닫혀있는 subset에서는 스칼라 곱에 다른 스칼라 곱을 곱하더라도 치환하면 단순한 스칼라 곱이 됩니다.
- 따라서 위의 주황색 글씨 처럼 $ac_{1}$은 $c_{4}$ 처럼 치환 됩니다.

$6$

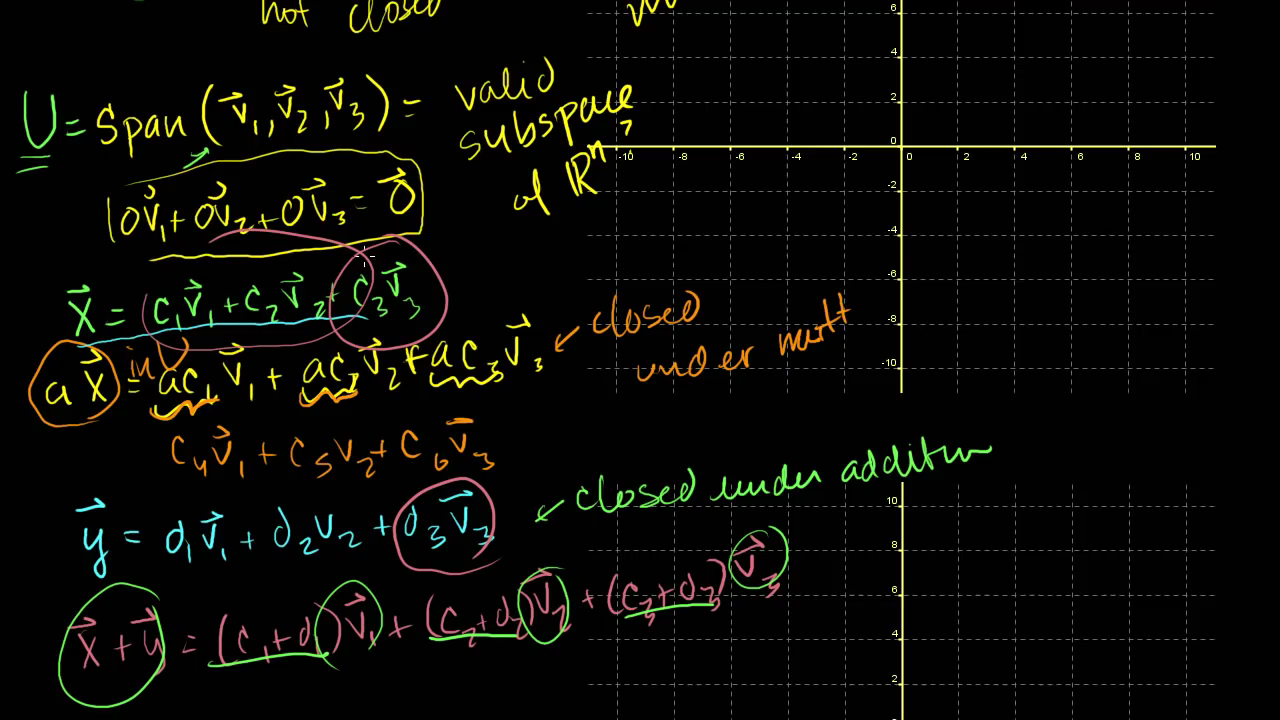
자주색 식을 보면 $\vec{x} + \vec{y}$ 식을 전개 하여 같은 항 끼리 묶으면 선형결합이 됩니다.
즉, 덧셈과 스칼라 곱에 대하여 닫혀있는 subset 상태에서의 연산은 즉, subspace의 연산은 또 다른 선형 결합을 만들어 냅니다.

$7$

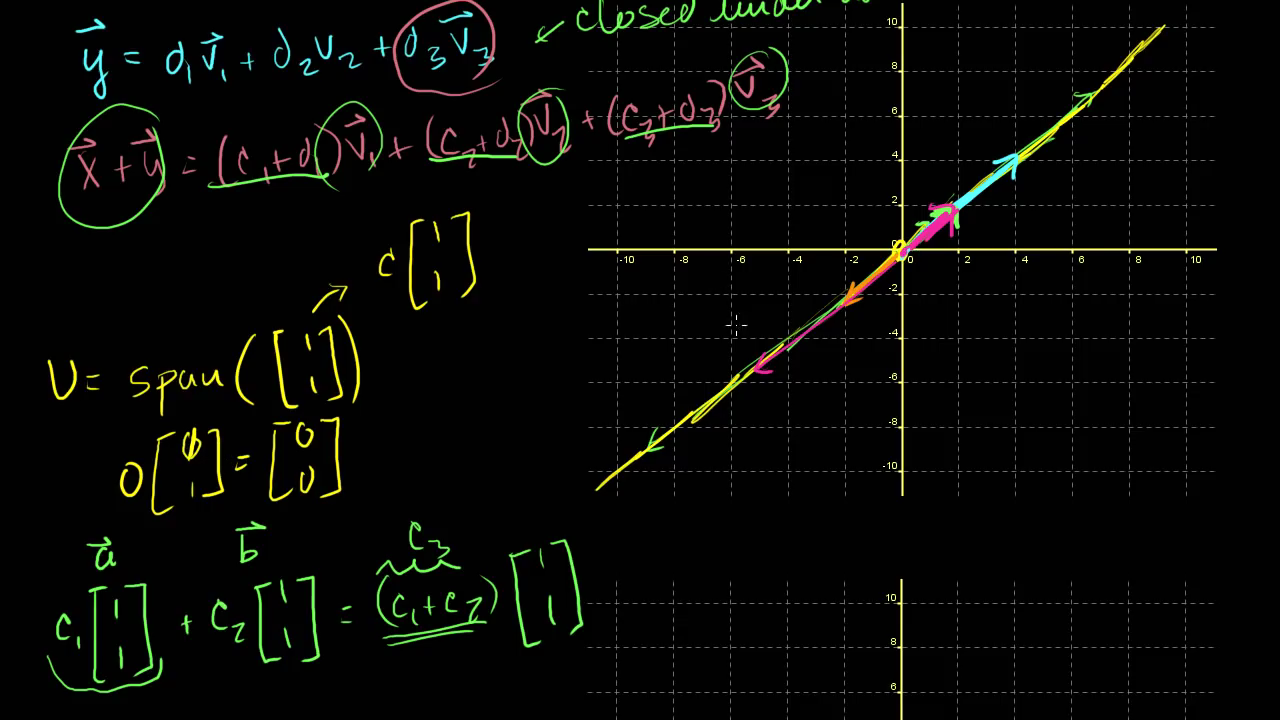
마지막 예제를 끝으로 subspace을 마무리 지어보겠습니다.

만약 $V = Span(\[1, 1\]^{T})$ 이라면 V의 subspace 는 직선에 머물게 되곘습니다.
이 때, 비록 subspace는 직선에 불과하지만 그것 또한 공간을 만들어 낼 수 있습니다.
- 예를 들어 스칼라 곱을 할 때 0을 곱하면 subspace에 속하게 됩니다.