Decision Tree (Reference ML KAIST)

Before dividing into Decision Tree, what is machine learning?

A computer program is said that
- learn from experience E
- With respect to some class of tasks T
- And performance measure P, if its performance at tasks in T, as measured by P, improves with experience E

A Perfect World for Rule Based Learning

Imagine a perfect world with

No observation errors, No inconsistent observations.
- (Training data is error-free, noise-free)
No stochastic elements in the system we observe.
- (Target function is deterministic)
Full information in the observations to regenerate the system
- (Target function is contained in hypotheses set)

Observation of the people

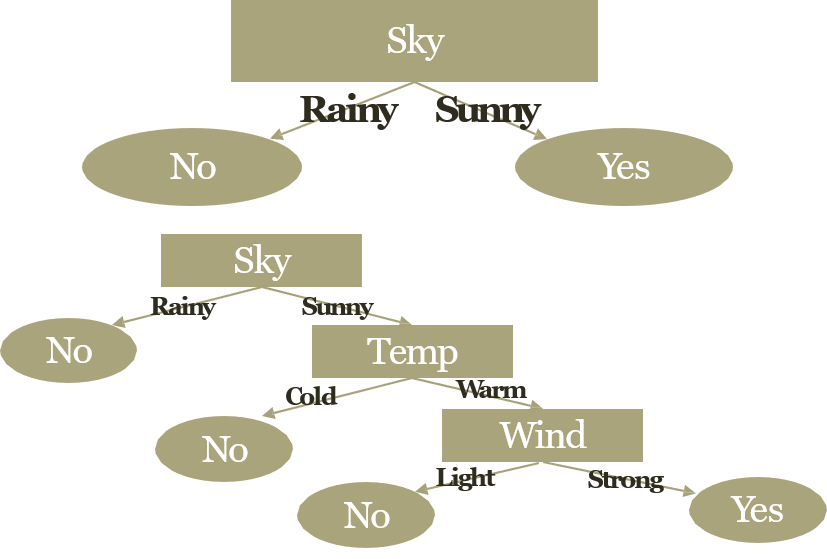
Sky, Temp, Humid, Wind, Water, Forecast → EnjoySport

Sky	Temp	Humid	Wind	Water	Forecast	EnjoySport
Sunny	Warm	Normal	Strong	Warm	Same	Yes
Sunny	Warm	High	Strong	Warm	Same	Yes
Rainy	Cold	High	Strong	Warm	Change	No
Sunny	Warm	High	Strong	Cool	Change	Yes

Function Approximation

Machine learning is relative to applying function approximation well.

Machine Learning ?
- The effort of producing a better approximate function
In the perfect world of EnjoySport
- Instance X
  - Features : <Sunny, Warm, Normal, Strong, Warm, Same>
  - Label : Yes
- Training dataset D
  - A collection of observations on the instance (Collection of Xs)
- Hypothesis H
  - Potentially possible function to turn X into Y
  - h_i : <Sunny, Warm, ?, ?, ?, Same> → Yes
- Target function C
  - Unknown target function between the features and the label
  - Our objective is expressing hypothesis H to target function C.

Graphical Representation of Function Approximation

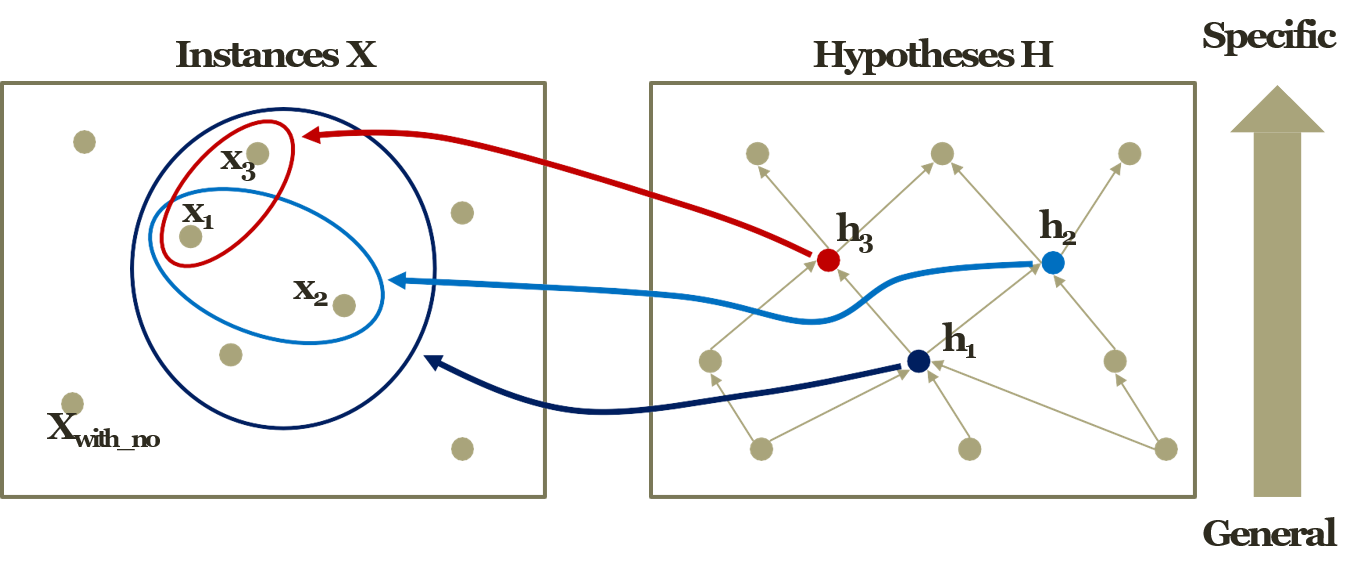
x1 : <Sunny, Warm, Normal, Strong, Warm, Same>, h1 : <Sunny, ?, ?, ?, Warm, ?>
x2 : <Sunny, Warm, Normal, Light, Warm, Same>, h2 : <Sunny, ?, ?, ?, Warm, Same>
x3 : <Sunny, Warm, Normal, Strong, Warm, Change>, h3 : <Sunny, ?, ?, Strong, Warm, ?>
What would be the better function approximation?
- Generalization Vs. Specialization
- Instance x1 & Hypothesis h1 is Generalization
- Instance x3 & Hypothesis h3 is Specialization

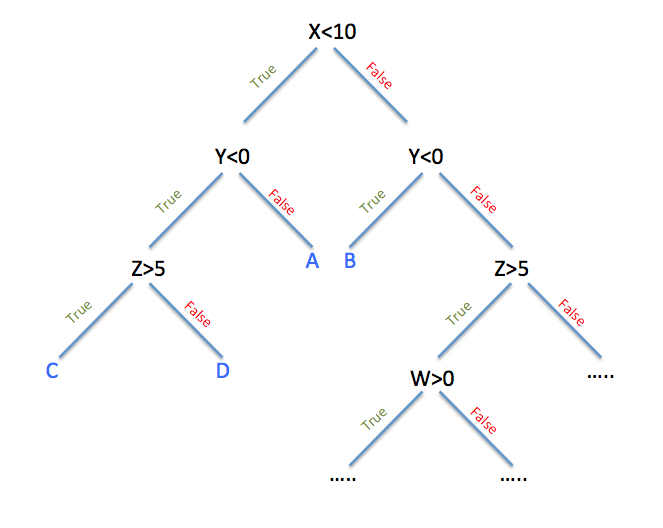
Find-S Algorithm

Find-S

Find-S Algorithm
- Initialize h to the most specific in H
- For instance x in D
  - if x is positive
    - For feature f in O
      - if \(f_{i}\) in h == \(f_{i}\) in x
        
        Do nothing
      - else
        
        (\(f_{i}\) in h) ← (\(f_{i}\) in h) \(\cup\) (\(f_{i}\) in x)
- Return h

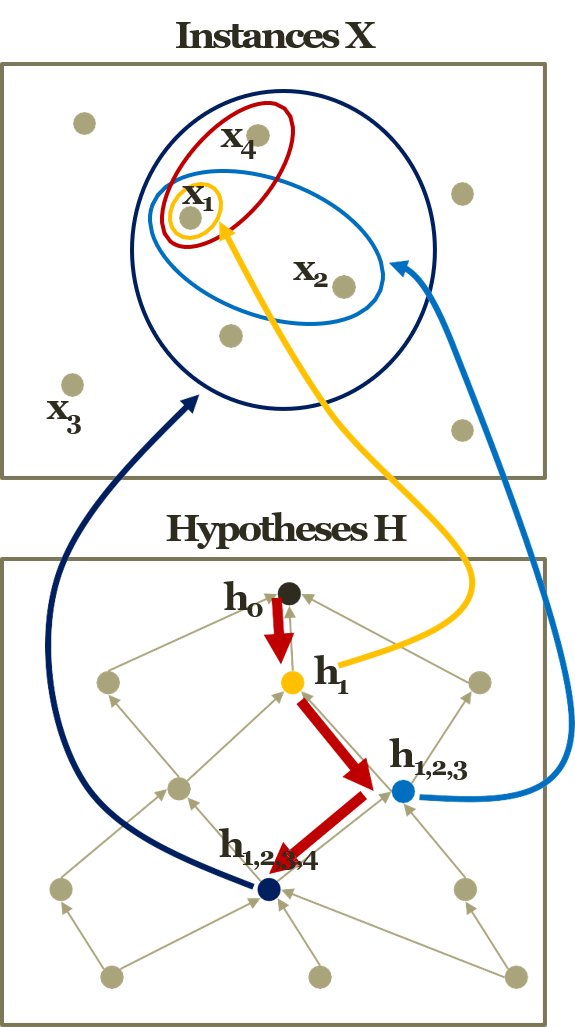
For example,

Instances
- \(x_{1}\) : <Sunny, Warm, Normal, Strong, Warm, Same>
- \(x_{2}\) : <Sunny, Warm, Normal, Light, Warm, Same>
- \(x_{4}\) : <Sunny, Warm, Normal, Strong, Warm, Change>
Hypothesis
- \(h_{0}\) = \(<\varnothing, \varnothing, \varnothing, \varnothing, \varnothing \varnothing>\)
- \(h_{1}\) = <Sunny, Warm, Normal, Strong, Warm, Same>
- \(h_{1,2}\) = <Sunny, Warm, Normal, Don’t care, Warm, Same>
- \(h_{1,2,4}\) = <Sunny, Warm, Normal, Don’t care, Warm, Don’t care>
Any possible problems?
- Many possible hs, and can’t determine the coverage.

we live with noises

We need a better learning method
- We need to have more robust methods given the noises
- We need to have more concise presentations of the hypotheses
One alternative is a decision tree.

decision tree

Good decision tree split the data as good ratio. Above example, A1 or A9 are features. In the case of A9, we have two options, True/False. If we choose True(left) then, we get correct answer 284/307. otherwise, 306/383, which is not good but not bad result.

In the decision tree, we should consider how to split the data in order to get good results.

Entropy

Better attribute to check?
- Reducing the most uncertainty
- Then, how to measure the uncertainty of a feature variable
Entropy of a random variable
- Features are random variables
- Higher entropy means more uncertainty
- \[H(x) = -\sum_{x}P(X=x)H(X=x)\]
Conditional Entropy
- We are interested in the entropy of the class given a feature variable
- Need to introduce a given condition in the entropy
- \[H(Y|X) = \sum_{x}P(X = x)H(Y | X = x) = \sum_{x}P(X = x){-\sum_{Y}P(Y = y | X = x)log_{b}P(Y = y | X = x)}\]