Evaluating a Learning Algorithm (Andrew Ng)

2019, Apr 12    

출처 : Andrew Ng 강의

• 이번 글에서는 학습 알고리즘을 평가하는 방법에 대하여 간략하게 알아보도록 하겠습니다.

• 위 슬라이드와 같이 cost function이 이와 같이 정의가 되어있다고 가정합시다.
• 위 cost function은 linear regression에서의 기본적인 cost function이고 regularization이 적용된 형태입니다.
• 만약 cost가 너무 크다면 step-by-step으로 접근하여 알고리즘을 수정할 필요가 있습니다.
  • 먼저 가장 효과적인 방법은 training data를 늘리는 방법입니다.
  • 그리고 학습데이터의 feature의 갯수를 작게 시작해서 더 늘려가는 방법이 좋습니다.
  • 또한 feature의 의미를 잘 이해하고 있다면 feature를 더 의미있게 활용하거나 가중치를 주기 위하여 polynomial feature를 사용하는 것도 추천합니다.
  • 그리고 regularization을 사용한 형태라면 \(\lambda\)의 크기를 변형하는 것도 학습에 도움이 됩니다.
• 아래 슬라이드는 대표적인 불안정한 학습 상태인 overfitting 입니다.

• 만약 위 슬라이드 처럼 fitting되었다면 학습 데이터에 너무 맞춰져서 새로운 데이터가 들어왔을 때 좋은 성능을 내기 어려울 수 있습니다.
• 특히 위와 같이 feature의 갯수가 너무 많다면 overfitting될 가능성이 더 커집니다.

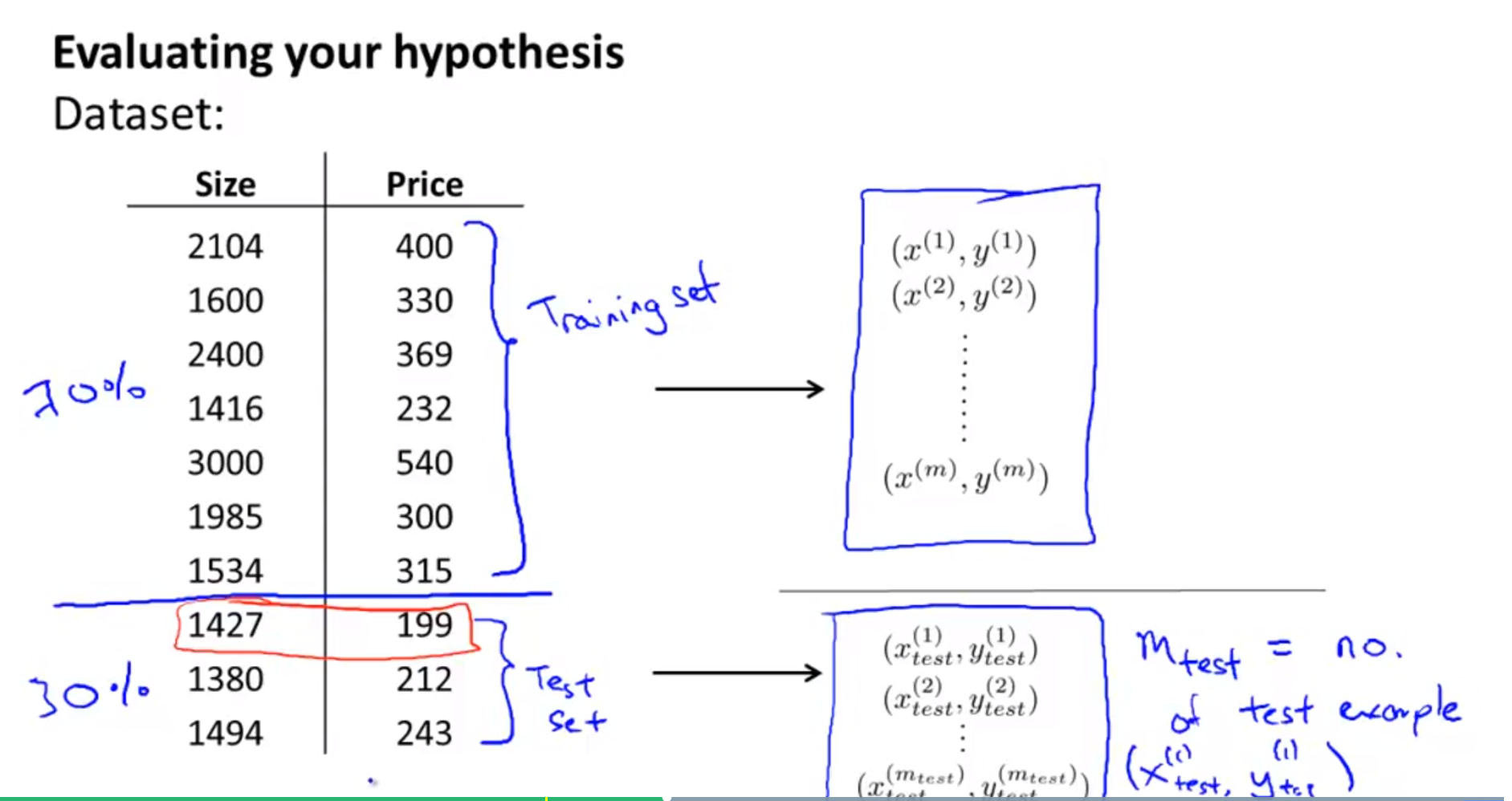
• 학습 알고리즘의 성능을 평가하기 위해서는 데이터 셋을 나누어야 합니다. 학습할 데이터와 테스트할 데이터가 필요합니다.
• 당연히, 학습 데이터의 양이 훨씬 더 많아야 합니다. 위 슬라이드의 학습 데이터의 비율을 70%를 한 것은 한가지 예이고 일반적으로 훨씬 더 많은 데이터를 학습에 사용합니다.
• 학습 데이터와 테스트 데이터의 비율이 정해지면, 순서에 맞게 분할할 수도 있지만 랜덤으로 선택하여 데이터를 분할하는 방법을 많이 사용합니다.
  • 랜덤으로 데이터를 선택하면 혹시나 있을 수 있는 데이터 편향 문제를 방지할 수도 있습니다.

• training data를 이용하여 파라미터 \(\theta\)의 학습을 하여 training data의 error를 먼저 구합니다.
• 그리고 학습한 결과를 이용하여 test data를 이용하여 error를 구하면 성능을 평가할 수 있습니다.
• 가장 전형적인 overfitting의 예시는 training data에서의 error는 낮은 반면 test data에서의 error는 높은 경우 입니다.

• 테스트를 할 때 모델의 성능을 cost function으로도 가늠할 수 있지만 좀 더 직접적인 성능 지표로 확인할 수 있습니다.
• classification 문제를 예를 들면 잘못 분류한 경우를 카운트 하여 Error율을 계산할 수 있습니다.
  • 위 슬라이드의 logistic regression 예제를 보면 모델이 \(h_{\theta}(x) \ge 0.5\)인 경우를 0으로 판별하면 error 라고 판단합니다.
  • 반대로 \(h_{\theta}(x) \lt 0.5\)인 경우를 1으로 판별하면 error 라고 판단합니다.

• 앞에서 살펴 보았듯이 overfitting이 training data에 대하여 발생하면 Training error는 generalization error보다 작다고 말할 수 있습니다.

• 그렇다면 우리의 학습 알고리즘의 목적 중 하나는 generalization error를 최대한 줄여 Training error과의 차이를 줄이는 것이라고도 할 수 있습니다.
• 이 때, 다양한 시도를 통하여 generalization error를 줄일 수 있는 데 그 시도 방법 중 하나는 적합한 model을 선택 하는 것입니다.
• 만약 위 슬라이드처럼 다항식의 차수가 다른 모델 10가지가 있다고 가정하겠습니다. 그리고 앞에서 다룬것 처럼 training/test data 셋 2개로 나누었다고 가정합시다.
• 이 10가지 모델 각각을 이용하여 training data에 대하여 학습시켰습니다. 이제 남은건 test data 입니다.
• test data에 대하여 cost를 확인해 보고 cost가 작은 것을 선택 하면 적합한 모델 선택을 한 것일까요?
• 이 방법의 문제는 위 슬라이드에 적혀있는 것 처럼 모델을 선택하는 것 또한 학습의 과정이라고 본다면 학습 과정에 test data가 개입하게 된 것입니다.
• 즉, 모델 선택 기준이 test data 기준이 되었고 신규 데이터에 대한 generalization error가 줄어들 것이라 장담할 수 없습니다.

• 이 문제를 해결하기 위하여 train/test data 이외에 validation data가 필요하게 됩니다.
• train data에서는 feature의 parameter를 학습하는 것이 초점이라면 validation data에서는 parameter 이외의 조건에 대하여 최적화 기준이 됩니다.
  • 이렇게 data를 분리해서 사용하면 test data는 학습에 전혀 개입하지 않게 되어 test 고유의 역할에 중점을 둘 수 있습니다.

• 따라서 각각의 data 셋에 대하여 위와 같이 error를 계산할 수 있습니다.
  • 다시 한번 정리하면
  • train data : 파라미터 학습
  • validation data : 파라미터 이외의 조건에 대한 학습
  • test data : generalization 성능 확인

• 따라서 앞에서 다루었던 model을 선택하는 문제에서 validation 데이터 셋을 도입함으로써 위 슬라이드 처럼 접근 하여 해결할 수 있습니다.

• 위 슬라이드는 일반적으로 많이 사용하는 평가 방법 중의 하나 입니다. 앞에서 소개한 training/test data를 분리하는 것에서 Cross Validation이라는 것이 도입되었습니다.