CCW(counter clockwise)

어떤 두 벡터의 방향 관계성을 보기 위해서는 어떤 벡터 $v_{1}$에서 또 다른 벡터 $v_{2}$로 회전 시 시계 방향(clockwise)으로 회전 하는 지 , 반시계 방향(counter clockwise)으로 회전 하는 지 를 통하여 알 수 있습니다.
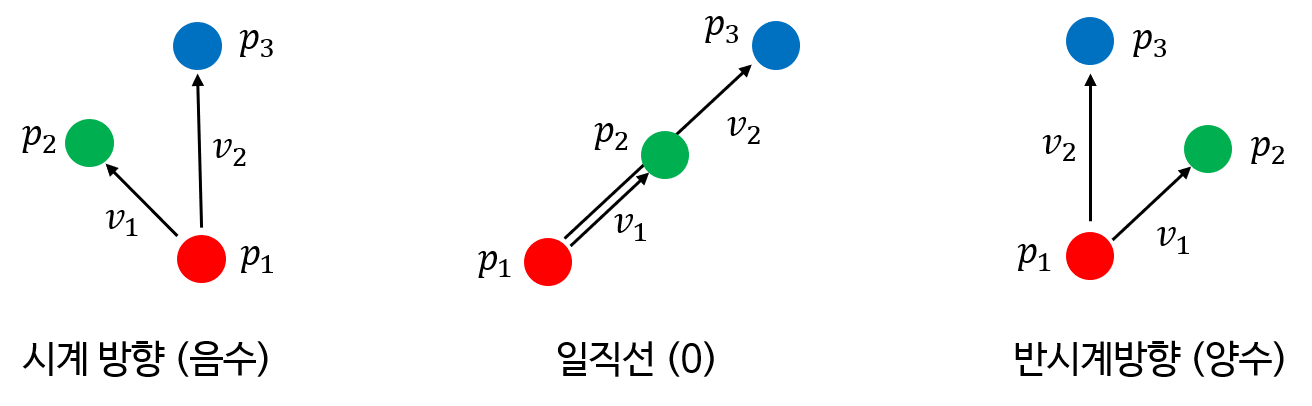
또는 세 점의 방향 관계성이라고 생각할 수도 있는 것이 세 점 $p_{1}, p_{2}, p_{3}$이 있다고 하였을 때, $v_{1}$이 $p_{1}, p_{2}$를 이은 벡터이고 $v_{2}$가 $p_{2}, p_{3}$를 이은 벡터라고 생각하면 세 점이 어떤 방향으로 위치해 있는 지 알 수 있습니다.

$Drawing$

이 관계는 벡터의 외적을 통하여 방향성을 확인 할 수 있는데 외적에 관한 자세한 내용은 다음 링크를 확인하시기 바랍니다.
- 참조 : https://gaussian37.github.io/math-la-cross-product/
벡터의 외적은 3차원 좌표계에서 계산할 수 있습니다. 즉, 반드시 한 개의 벡터에 3차원의 정보가 있어야 한다는 뜻입니다.
예를 들어 두 벡터가 3차원에 존재한다면 $\bar{v}_{1} = (x_{1}, y_{1}, z_{1})$과 $\bar{v}_{2} = (x_{2}, y_{2}, z_{2})$가 있고 이 두 벡터의 외적을 통하여 $v_{1}$이 $v_{2}$에 대하여 시계방향에 있는지 반시계방향에 있는지 확인할 수 있습니다.
만약 2차원에 존재하는 점이라면 z축의 값을 0으로 두면 됩니다. 즉, $\bar{v}_{1} = (x_{1}, y_{1}, 0)$과 $\bar{v}_{2} = (x_{2}, y_{2}, 0)$로 하여 한 축을 무시해 버리면 2차원 좌표에서도 벡터의 외적을 적용할 수 있습니다.
그러면 외적의 값에 따라서 어떻게 방향을 구분할 수 있을까요?
외적의 결과값이 음수이면 시계방향이고 양수이면 반시계방향입니다. 0이면 일직선 방향입니다. 현재 알고리즘의 이름이 CCW(반시계방향)이므로 양수이면 반시계방향이라는 것만 일단 숙지하시면 도움이 됩니다.

\[p_{1} \times p_{2} = \text{det} \begin{pmatrix} x_{1} & x_{2} \\ y_{1} & y_{2} \end{pmatrix} = x_{1}y_{2} - x_{2}y_{1} = -p_{2} \times p_{1}\]

\[v_{1} \times v_{2} = (x_{2} - x_{1})(y_{3} - y_{1}) - (x_{3} - x_{1})(y_{2} - y_{1})\]

위 코드의 ccw 함수는 세 점 $p_{1}, p_{2}, p_{3}$의 좌표값을 입력으로 넣으면 출력으로 1, 0, -1을 반환해 줍니다.
결과값은 $p_{1}, p_{2}$가 이루는 벡터를 기준으로 $p_{1}, p_{3}$가 이루는 벡터의 위치를 나타내고 1은 반시계 방향(counter clockwise), 0은 겹치는 방향 (collinear), -1은 시계 방향(clockwise)이 됩니다.