(CLRS) 선분의 교차성 결정

이 글은 CLRS(Introduction to algorithm) 책을 요약한 것이므로 자세한 내용은 CLRS 책을 참조하시기 바랍니다.
CLRS 내용 외에 따로 정리한 선분의 성질 관련 블로그 글은 아래 링크를 참조하시기 바랍니다.
- CCW : https://gaussian37.github.io/math-algorithm-ccw/
- 선분의 교차 : https://gaussian37.github.io/math-algorithm-line_intersection/

이전 글에서 살펴본 내용은 선분이 2개가 있을 때, 2개의 선분의 관계에 대하여 알아보았습니다.
이번 글에서 살펴볼 내용은 임의의 선분 n개가 존재할 때, n개의 선분들 사이에 교차되는 점이 있는 지, 선분들 간의 관계를 알아보도록 하겠습니다.
선분의 교차성을 판단하는 알고리즘의 시간 복잡도는 $O(nlgn)$ 이 됩니다. 여기서 $n$은 주어진 선분의 수를 나타냅니다.
책에서 설명하는 알고리즘은 교차점이 존재하는 지 여부만을 나타내고 연습문제에서 모든 교차점을 찾는 데 걸리는 수행시간을 다룹니다. 이 때에는 $O(n^{2})$이 걸리게 됩니다.

$Drawing$

검사 방법을 sweeping 이라고 하는데 그 이유는 왼쪽에서 부터 오른쪽으로 쓸어가듯이 검사하기 때문입니다. sweeping을 할 때에는 수직 성분의 sweep line이 필요합니다. 이 sweep line이 왼쪽에서 오른쪽으로 쓸어갑니다. 위 그림에서 수직 점선이 sweeping line에 해당합니다.
그러면 x차원(가로 축)의 sweep line이 이동하는 영역은 마치 시간 영역 처럼 나타나집니다. 마치 시간이 흐르는 것 처럼 왼쪽에서 부터 시작해서 오른쪽으로 이동하면서 새로운 영역을 보기 때문입니다.
이 때, 저희가 살펴볼 영역은 모든 선의 성분이 아니라 선의 양 끝점입니다. 즉, 선분 교차 알고리즘은 모든 선분의 끝점을 좌에서 우로 검사하면서 끝점을 지날 때 마다 교차 여부를 조사합니다.
추가적으로 이 글에서는 알고리즘의 정당성을 확인하기 위해 문제를 좀 더 쉽게 가정하려고 합니다.
- 1) 어떤 선분도 수직은 아니다.
- 2) 어떤 세 선분도 한 점에서 만나지 않는다.

선분의 순서화

수직 성분이 존재하지 않는 다는 가정을 통하여 수직 검사선을 교차하는 입력 선분의 위치는 한 개의 점이 됩니다.
따라서 교차하는 점들의 y 좌표에 의해 검사선과 수직으로 교차하는 선분을 차례대로 순서를 정할 수 있습니다. 이것을 선분의 순서화라고 하겠습니다.
선분을 순서화 하려면 수직 sweeping line을 통하여 검사할 때, 선분 끼리 비교가 가능해야 합니다.
예를 들어 두 선분 $s_{1}, s_{2}$가 있다고 가정해 보겠습니다. 만약 수직으로 검사선의 $x$ 좌표와 교차점 $x$가 양쪽을 교차하면, 이런 선분을 $x$에서 비교 가능하다고 할 수 있습니다.

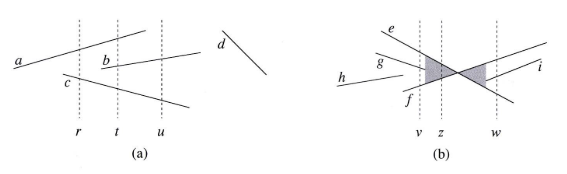
$Drawing$

예를 들어 왼쪽 (a) 그림을 한번 살펴보도록 하겠습니다.
r sweeping line과 만나는 선분은 $a$와 $c$ 두 개가 있습니다. 이 때, $y$ 좌표는 어떤 선분이 큰가요? 바로 $a$ 입니다.
sweeping line은 $x$축에 수직인 직선이기 때문에 $x$값은 같습니다. 따라서 선분의 비교는 $y$ 값을 통해 할 수 있습니다.
이 때 비교할 때 사용된 sweeping line을 이름을 이용하여 부등호를 $\gt_{r}$ 형태로 사용할 수 있습니다. 그러면 $a \gt_{r} c$로 표현할 수 있습니다.
그러면 (a) 그림에서 비교 가능한 쌍을 보면 $a \gt_{r} c$, $a \gt_{t} b$, $b \gt_{t} c$, $b \gt_{u} c$ 가 됩니다. 그리고 선분 $d$는 sweeping line과 교차하는 다른 선분이 없으므로 비교가 불가능 합니다.

하지만 선분의 순서가 계속 유지되는 것은 아닙니다. (b) 그림을 보면 선분이 교차하는 경우 sweeping line에서 선분의 순서가 바뀌는 것을 확인할 수 있습니다.
(b) 그림에서 sweeping line $v, w$를 보면 $e \gt_{v} f$ 이지만 $f \gt_{w} e$가 됩니다.

이 글에서 다루는 sweeping-line algorithm은 데이터 집합 2개를 관리해야 합니다.
- sweep-line status : 검사선에 의해 교차되는 객체 사이의 관계를 제공합니다. 이 status는 balanced binary tree (ex. red-black tree)에 저장합니다.
- event-point schedule : 검사선의 정지 장소를 정의하는 x좌표의 수열로 왼쪽에서 오른쪽으로 정렬되어 있습니다. 알고리즘에서 이 정지 장소를 사건 점(event point)이라고 합니다. 검사가 왼쪽에서 오른쪽으로 진행 될 때, 실제 검사 즉, sweeping 이 발생하는 지점은 event point에서만 발생하게 됩니다.
먼저 주어진 선분 셋에서 event-point들을 이용하여 선분들을 정렬해서 배열에 저장합니다. 이 때, 이 event-point가 선분의 왼쪽점인 지 오른쪽 점인 지 같이 저장해야 합니다.
선분들의 끝점을 이용하여 $x$ 좌표의 오름차순으로 정렬하는데 왼쪽에서 오른쪽 순서로 저장합니다.
만약 두개 이상의 끝점이 $x$ 좌표가 같은 공동 수직선에 있다면 $y$ 좌표가 작은 순서대로 저장합니다.
정리하면 (① x 좌표가 작은 순서, ② y좌표가 작은 순서의 우선순위로 저장) + 선분의 왼쪽 좌표/오른쪽 좌표 정보 저장 한다고 보면 됩니다.

sweeping line이 왼쪽 끝점을 만나면 선분을 sweep-line status에 삽입하고, 오른쪽 끝점을 만나면 선분을 sweep-line status에서 삭제합니다.