(CLRS) 삽입정렬과 알고리즘 분석
2020, Apr 10
- 이 글은 CLRS(Introduction to algorithm) 책을 요약한 것이므로 자세한 내용은 CLRS 책을 참조하시기 바랍니다.
삽입 정렬
- 삽입 정렬은 가장 쉬운 정렬 알고리즘 중의 하나입니다. 물론 입력 값의 갯수가 많으면 상당히 비효율적이기 때문에 사용하면 안되지만 입력값의 갯수가 작을 때에는 재귀 호출 등의 추가 비용이 없기 때문에 제한적으로 사용할 수도 있습니다.
- 이 글에서는 삽입 정렬을 이용하여 알고리즘의 분석 및 설계를 하는 방법에 대하여 다루어 보도록 하겠습니다.
Insertion Sort의pseudo code에 대하여 알아보겠습니다.- 입력 : n개 수의 수열 \(a_{1}, a_{2}, \cdots , a_{n}\) 아래 pseudo code에서는 배열 \(A[ 1 ... n ]\)으로 나타남
- 출력 : \(a_{1}' \ge a_{2}' \ge \cdots \ge a_{n}'\)으로 오름차순 정렬된 수열

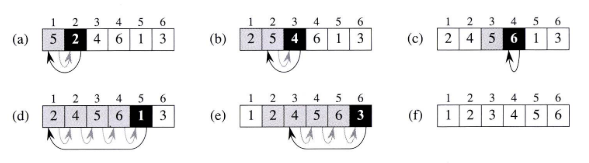
- 위 pseudo code가 동작하는 방식은 아래 그림과 같습니다.
루프 불변성 (수학적 귀납법)의 타당성 증명
- 먼저 루프 불변성의 3가지 조건인
초기 조건,유지 조건,종료 조건에 대하여 알아보고 이 개념을 삽입 정렬에 적용시켜 보겠습니다. 초기 조건(베이스 케이스): 루프의 첫 반복을 시작하기 전에 루프 불변성이 참이어야 합니다.유지 조건(귀납 가정 - 귀납 증명): 루프의 반복이 시작되기 전에 루프 불변성이 참이었다면 다음 반복 시작 시에도 참이어야 합니다.종료 조건: 루프가 종료가 될 때 루프 불변성이 알고리즘의 타당성을 보이는 데 도움이 될 유용한 특성을 가져야 합니다.
삽입 정렬의 루프 불변성
초기 조건: 루프 카운트 변수가 초기화되어 \(j = 2\) 일 때, \(A[1, \ ..., \ j-1]는\) A[1] $$이므로 루프 불변성은 참이 됩니다.유지 조건: \(A[j]\)의 위치를 찾을 때 까지 \(A[j-1], A[j-2], ...\)을 오른쪽으로 이동시킨 뒤 (위 pseudo code의 4 ~ 7행), 적절한 위치에 삽입하면 (8행), \(A[1,\ ...\ , j]\)는 for 루프의 다음 반복에서 루프 불변성이 참으로 유지됩니다.종료 조건: \(j = n + 1\)일 때 종료하며, 이 때, \(A[1,\ ...\ , n]\)이 모두 정렬되었기 때문에 알고리즘은 타당합니다.
알고리즘의 분석
- 알고리즘 분석 시 분석대상은
수행 시간 계산이 주 목적이 됩니다. - 알고리즘의 동작 환경은
단일 프로세서에랜덤 접근 기계 모델을 사용합니다. 즉, 차례로 하나씩 명령어를 실행하고 하드웨어 성능 및 특성은 고려하지 않습니다. 예를 들어 데이터 형이나 연산 종류 또는 메모리 계층(캐쉬 메모리, 가상 메모리) 같은 것은 고려하지 않습니다. - 삽입 정렬 알고리즘의 분석을 해보도록 하겠습니다.

- 위 pseudo code의
cost는 수행 시간을 뜻하고time은 연산 횟수라고 생각하시면 됩니다. - 이 때, 삽입 정렬 알고리즘의 수행시간은 다음과 같습니다.
- \[T(n) = c_{1}n + c_{2}(n-1) + c_{4}(n-1) + c_{5}\sum_{j=2}^{n}t_{j} + c_{6}\sum_{j=2}^{n}(t_{j} - 1) + c_{7}\sum_{j=2}^{n}(t_{j} - 1) + c_{8}(n-1)\]
- 최선의 경우(\(an + b\))는 다음과 같습니다.
- \[T(n) = c_{1}n + (c_{2} + c_{4} + c_{8})(n-1) + c_{5}(n-1) = (c_{1} + c_{2} + c_{4} + c_{5} + c_{8})n - (c_{2} + c_{4} + c_{5} + c_{8})\]
- 최악의 경우(\(an^{2} + bn + c\))는 다음과 같습니다.
- \[T(n) = \Biggl(\frac{c_{5}}{2} + \frac{c_{6}}{2} + \frac{c_{7}}{2} \Biggr)n^{2} + \Biggl(c_{1} + c_{2} + c_{4} + \frac{c_{5}}{2} - \frac{c_{6}}{2} - \frac{c_{7}}{2} + c_{8} \Biggr)n - (c_{2} + c_{4} + c_{5} + c_{8})\]