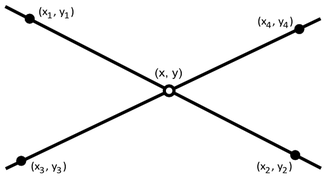
두 선분(직선)의 교점
2020, Mar 02
- 출처 : https://zetawiki.com/wiki/두_직선의_교차점
목차
-
점의 좌표 4개가 주어졌을 때, 교점
-
표준형 식에서의 교점
-
일반형 식에서의 교점
-
C 코드
- 두 직선이 교차할 때, 두 직선의 교차점을 구하는 방법은 다양한 방법이 많습니다. 특히 손으로 풀 때에는 연립방정식을 이용하면 쉽게 구할 수 있습니다.
- 코드로 구할 때에는 closed form 형태로 함수를 마련해 놓아야 편리하기 때문에 이번 글에서는 함수 형태로 어떻게 나타냐면 되는 지 정리하겠습니다.
- 물론 코드의 안정성을 위하여 두 선분이 실제로 교차할 때에 한하여 교점을 찾는 것이 좋습니다. 두 선분의 교차 여부를 확인하기 위해서는 아래 링크를 참조하시기 바라니다.
- 두 선분의 교차 여부 확인 : https://gaussian37.github.io/math-algorithm-line_intersection/
점의 좌표 4개가 주어졌을 때, 교점
- 직선 A가 \((x_{1}, y_{1}), (x_{2}, y_{2})\)로 이루어져 있고 직선 B가 \((x_{3}, y_{3}), (x_{4}, y_{4})\)로 이루어져 있다면 두 직선의 교점은 다음과 같습니다.
- 이 때, 앞에서 언급한 방법으로 두 선분의 교차 여부를 확인해도 되지만 다음 방법을 사용해도 됩니다.
- 식의 분모에 해당하는 \((x_{1} - x_{2})(y_{3} - y_{4}) - (y_{1} - y_{2})(x_{3} - x_{4}) = 0\) 을 만족하면 두 직선은 평행 또는 일치합니다.
- \[(P_{x}, P_{y}) = \Biggl( \frac{ (x_{1}y_{2} - y_{1}x_{2})(x_{3} - x_{4}) - (x_{1} - x_{2})(x_{3}y_{4} - y_{3}x_{4})}{(x_{1} - x_{2})(y_{3} - y_{4}) - (y_{1} - y_{2})(x_{3} - x_{4})}, \frac{ (x_{1}y_{2} - y_{1}x_{2})(y_{3} - y_{4}) - (y_{1} - y_{2})(x_{3}y_{4} - y_{3}x_{4}) }{(x_{1} - x_{2})(y_{3} - y_{4}) - (y_{1} - y_{2})(x_{3} - x_{4})} \Biggr)\]
표준형 식에서의 교점
- 주어진 식이 다음과 같다고 가정해 보겠습니다.
- \[y = m_{1}x + b_{1}\]
- \[y = m_{2}x + b_{2}\]
- 이 때, 교점은 다음과 같습니다.
- \[(P_{x}, P_{y}) = \Biggl(\frac{b_{2} - b_{1}}{m_{1} - m_{2}}, m_{1}\frac{b_{2} - b_{1}}{m_{1} - m_{2}} + b_{1} \Biggr)\]
- 이 때에도 \(m_{1} - m_{2} = 0\)이면 두 직선은 평행 또는 일치합니다.
일반형 식에서의 교점
- 주어진 식이 다음과 같다고 가정해 보겠습니다.
- \[a_{1}x + b_{1}y + c_{1} = 0\]
- \[a_{2}x + b_{2}y + c_{2} = 0\]
- 이 때, 교점은 다음과 같습니다.
- \[(P_{x}, P_{y}) = \Biggl( \frac{b_{1}c_{2} - b_{2}c_{1}}{a_{1}b_{2} - a_{2}b_{1}} , -\frac{a_{1}}{b_{1}}\Biggl( \frac{b_{1}c_{2} - b_{2}c_{1}}{a_{1}b_{2} - a_{2}b_{1}} \Biggr) -\frac{c_{1}}{b_{1}} \Biggr)\]
- 이 때에도, \(a_{1}b_{2} - a_{2}b_{1} = 0\)이면 두 직선은 평행 또는 일치합니다.
C 코드
- 마지막으로 위에서 다룬 내용을 C 코드로 옮겨서 실행해 보도록 하겠습니다.
- 코드에서 다루어 볼 예제는 다음과 같습니다.
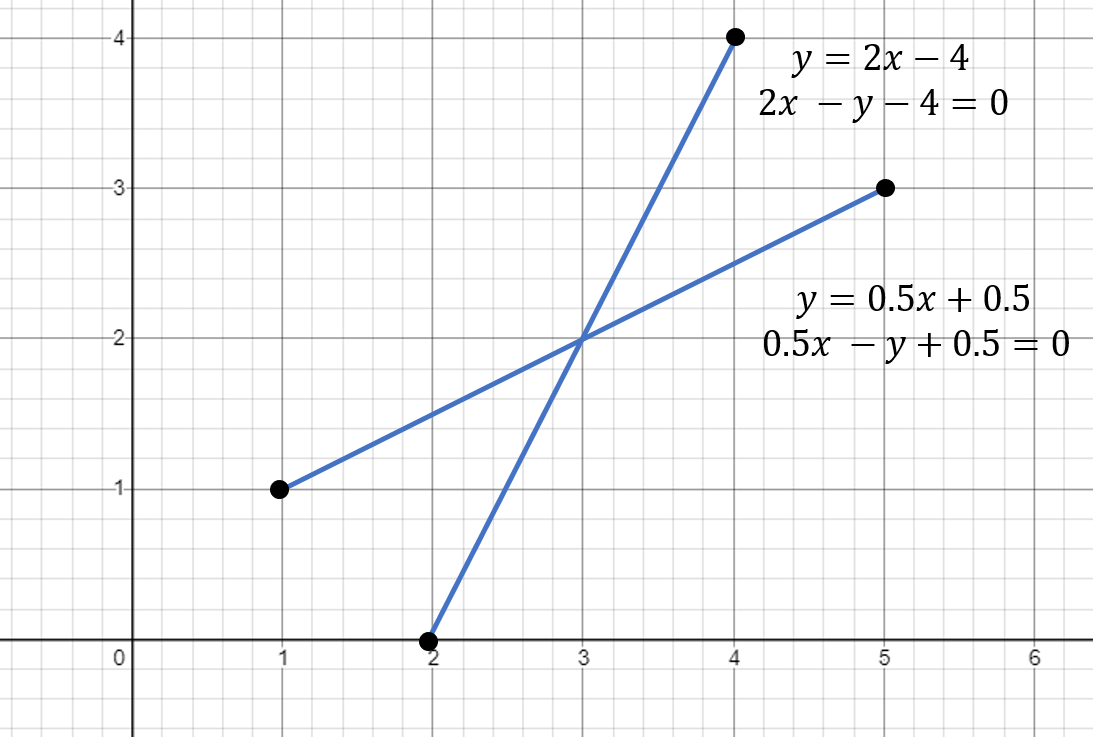
- 아래 코드의 각각의 함수는 4개의 점, 표준형 식, 일반형 식이 주어졌을 때, 교차점을 구하는 함수 입니다.