KD-Tree 정리
2023, Mar 02
목차
-
KD-Tree의 정의
-
KD-Tree의 차원 확장
-
Nearest Search KD-Tree
-
KNN Search KD-Tree
-
Radius Search KD-Tree
-
Hybrid KNN and Radius Search KD-Tree
KD-Tree의 정의
- 이번 글에서 다룰
KD-Tree는 \(K\) 개의Dimension을 이용하여Binary Tree를 만드는 자료 구조를 의미합니다. 즉, \(K\) 개 차원의Binary Search Tree의 자료구조를 의미합니다.KD-Tree를 이용하면 데이터셋에 대하여 평균적으로 \(\text{O}(\log{n})\) 만에 탐색이 가능하므로 효율적으로 탐색이 가능해 집니다. KD-Tree는Binary Search Tree를 \(K\) 차원으로 확장한 것이므로 2차원 또는 3차원의 데이터를 다룰 때 많이 사용됩니다. 예를 들어 3차원 상의 점들이 좌표값을 가질 때, 특정 점과 가장 가까운 점 또는 가장 가까운 점군들을 찾을 때 많이 사용됩니다. 이번 글에서도 다룰 예제는 3차원 포인트 클라우드를 이용하여KD-Tree를 만들고 임의의 점과 가장 가까운 점들을 찾는 예제를 위주로 살펴볼 예정입니다.
Binary Search Tree 예시
- 먼저
Binary Search Tree에 대하여 간략히 살펴보도록 하겠습니다.Binary Search Tree는 데이터를 효율적으로 검색하기 위하여 특정 노드를 기준으로 그 노드의 값보다 작은 값은 왼쪽으로 구성하고 그 노드의 값보다 큰 값은 오른쪽으로 구성하는 자료 구조를 의미합니다. - 이와 같이 트리를 구성하였을 때, \(\text{O}(\log{n})\) 으로 자료를 검색할 수 있다는 효율성이 있습니다. 아래 예시와 같습니다.
- \[3, 7, 10, 12, 17, 21\]
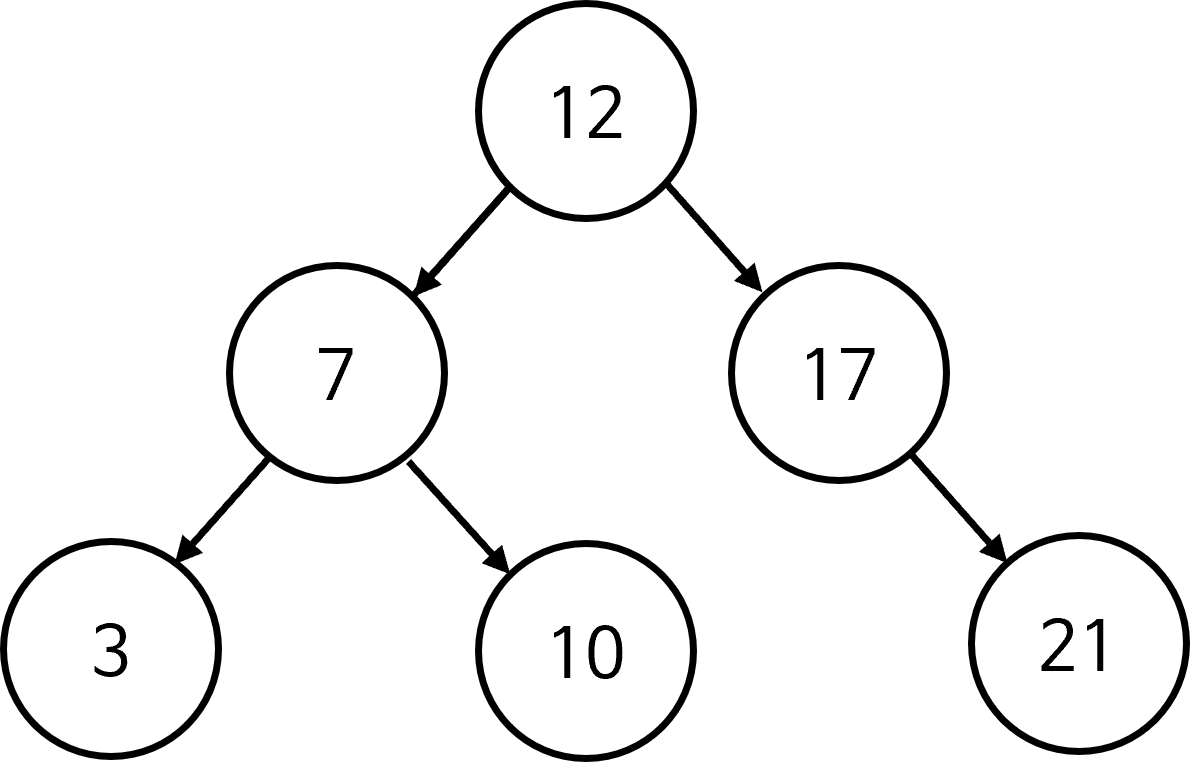
- 위 예시와 같이 6개의 데이터가 있을 때, 오름차순 정렬 후 가운데 노드를 기준으로 트리를 만들어 가면 위 그림과 같이 트리를 생성할 수 있습니다. 12보다 작은 3, 7, 10 은 왼쪽에 속하고 12보다 큰 12, 21 은 오른쪽에 속합니다. 위 그림에서는 3, 7, 10 중 가운데 값인 7을 기준으로 같은 방식으로 트리를 생성하였습니다.
Binary Search Tree가 좌/우 평형을 이루어 왼쪽과 오른쪽 트리의 크기가 비슷하다면 대략 \(\text{O}(\log{n})\) 시간에 탐색을 할 수 있습니다.
- 이 글에서 다루는
KD-Tre는 위 그림과 같이 차원이 1개가 아니라 차원이 \(k\) 개인 데이터를 다룹니다. 먼저 2차원 데이터를 기준으로 어떻게 트리를 구성하는 지 살펴보도록 하겠습니다.
2차원 KD-Tree 생성
KD-Tree는Binary Search Tree와 비교하였을 때 2가지 차이점을 가지고 있습니다. 먼저 ① 값을 비교하는 노드가 스칼라 값이 아닌 벡터로 2개 이상의 값을 가진다는 점이고 ② 정확히 노드의 값을 찾는 것이 아니라 노드와 가장 가까운 노드 찾는 것입니다.- ① 은 트리를
생성할 때 고려해야 할 문제이고 ② 는 생성된 트리에서 값을검색할 때 고려해야 할 문제입니다. 먼저 트리를 생성하는 방법에 대하여 살펴보도록 하겠습니다.
KD-Tree는Binary Search Tree와 다르게 각 노드의 차원이 \(K\) 개가 되므로 어떤 차원을 기준으로 트리를 구성해야 할 지 선택해야 합니다.
- \[X = (x_{1}, x_{2}, \cdots x_{K})\]
- 위 식의 \(X\) 는 1개의 노드를 의미합니다. \(X\) 는 \(K\) 개의 차원을 가지는 벡터이며 이러한 벡터가 노드가 되어서 트리를 구성합니다.
Binary Search Tree와 같이 특정 값을 이용하여 트리를 구성하려면 비교해야 할 값을 선택해야 합니다. 다음과 같이 \(K = 2\) 인 10개의 2차원 데이터 예제를 이용하여 살펴보겠습니다.
- \[X_{1} = (3, 1), X_{2} = (2, 3), X_{3} = (6, 2), X_{4} = (4, 4), X_{5} = (3, 6)\]
- \[X_{6} = (8, 5), X_{7} = (7, 6.5), X_{8} = (5, 8), X_{9} = (6, 10), X_{10} = (6, 11)\]
- 위 예제와 같이 10개의 2차원 데이터를 이용하여 트리를 구성하려고 할 때, 첫번째 차원과 두번째 차원 중 차원 하나를 먼저 선택한 다음에
Binary Search Tree를 구성해야 합니다. - 검색에 효과적인
Binary Search Tree를 생성하기 위해서는 특정 노드를 기준으로Left,Right로 트리를 분할하기 좋도록 만들어야 합니다. 따라서 ① 각 차원을 기준으로 분산을 구한 다음에 분산이 가장 큰 차원을 선택하고 ② 선택된 차원의 값들만 정렬한 후 중앙값(median)을 선택하면 분할 효과를 최대화할 수 있습니다. ① 차원 선택과② 분할 기준 선택을 통하여Left,Right를 분할하고 이 과정을 재귀적으로 반복하면KD-Tree를 생성할 수 있습니다.
- 위 10개의 데이터의 첫번째 축 값의 분산을 계산해 보도록 하겠습니다.
- \[\text{Mean}_{1} = \frac{3 + 2 + 6 + 4 + 3 + 8 + 7 + 5 + 6 + 6}{10} = 5\]
- \[\text{Variance}_{1} = \frac{(3-5)^{2} + (2-5)^{2} + (6-5)^{2} + \cdots + (6-5)^{2} + (6-5)^{2}}{10} = 3.4\]
- 다음으로 두번째 축 값의 분산을 계산해 보도록 하겠습니다.
- \[\text{Mean}_{2} = \frac{1 + 3 + 2 + 4 + 6 + 5 + 6.5 + 8 + 10 + 11}{10} = 5.65\]
- \[\text{Variance}_{2} = \frac{(1-5.65)^{2} + (3-5.65)^{2} + (2-5.65)^{2} + \cdots + (10-5.65)^{2} + (11-5.65)^{2}}{10} = 9.9025\]
- 따라서 두번째 축의 분산의 값이 9.9025 > 3.4 로 더 큰것을 확인할 수 있습니다. 즉, 두번째 축으로 데이터가 더 넓게 분포되어 있다는 뜻이며 두번째 축을 기준으로 데이터를 나누면 데이터를 더 많이 분할할 수 있음을 알 수 있습니다.
- 이 때 기준이 되는 노드는 두번째 축의 중앙값을 선택해야 합니다. 따라서 두번째 축을 기준으로 정렬한 다음 중앙값을 선택합니다.
- \[1 \lt 2 \lt 3 \lt 4 \lt 5 \lt 6 \lt 6.5 \lt 8 \lt 10 \lt 11\]
- 정렬하였을 때, 6이 중앙값에 해당하므로 \(X_{5} = (3, 6)\) 이 루트 노드가 됩니다.
- 루트 노드를 기준으로 두번째 축의 값이 6 보다 작은 노드들은 루트 노드를 기준으로 왼쪽에서 트리를 구성하고 두번째 축의 값이 6보다 큰 노드들은 루트 노드를 기준으로 오른쪽에서 트리를 구성합니다.
- \[\text{Left : } X_{1} = (3, 1), X_{2} = (2, 3) X_{3} = (6, 2) X_{4} = (4, 4) X_{6} = (8, 5)\]
- \[\text{Right : } X_{7} = (7, 6.5), X_{8} = (5, 8), X_{9} = (6, 10), X_{10} = (6, 11)\]
- 분할된 두 데이터셋을 같은 방법으로 재귀적으로 트리를 구성할 수 있습니다. 트리 구성을 완료하면 다음과 같습니다.
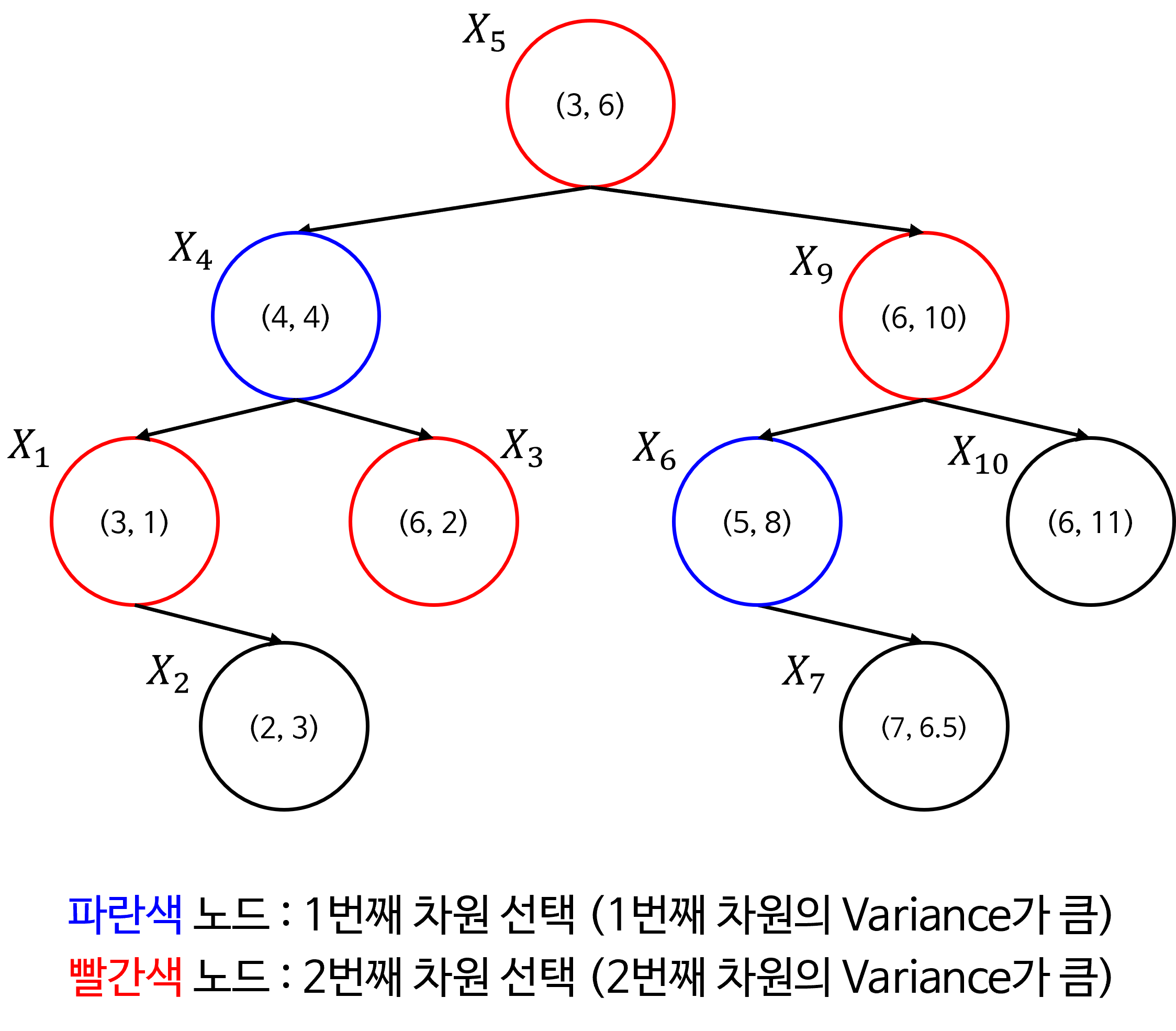
- 위 트리 구조를 2D 공간에 적용하여 시각화 하면 다음과 같이 공간을 분할할 수 있습니다.
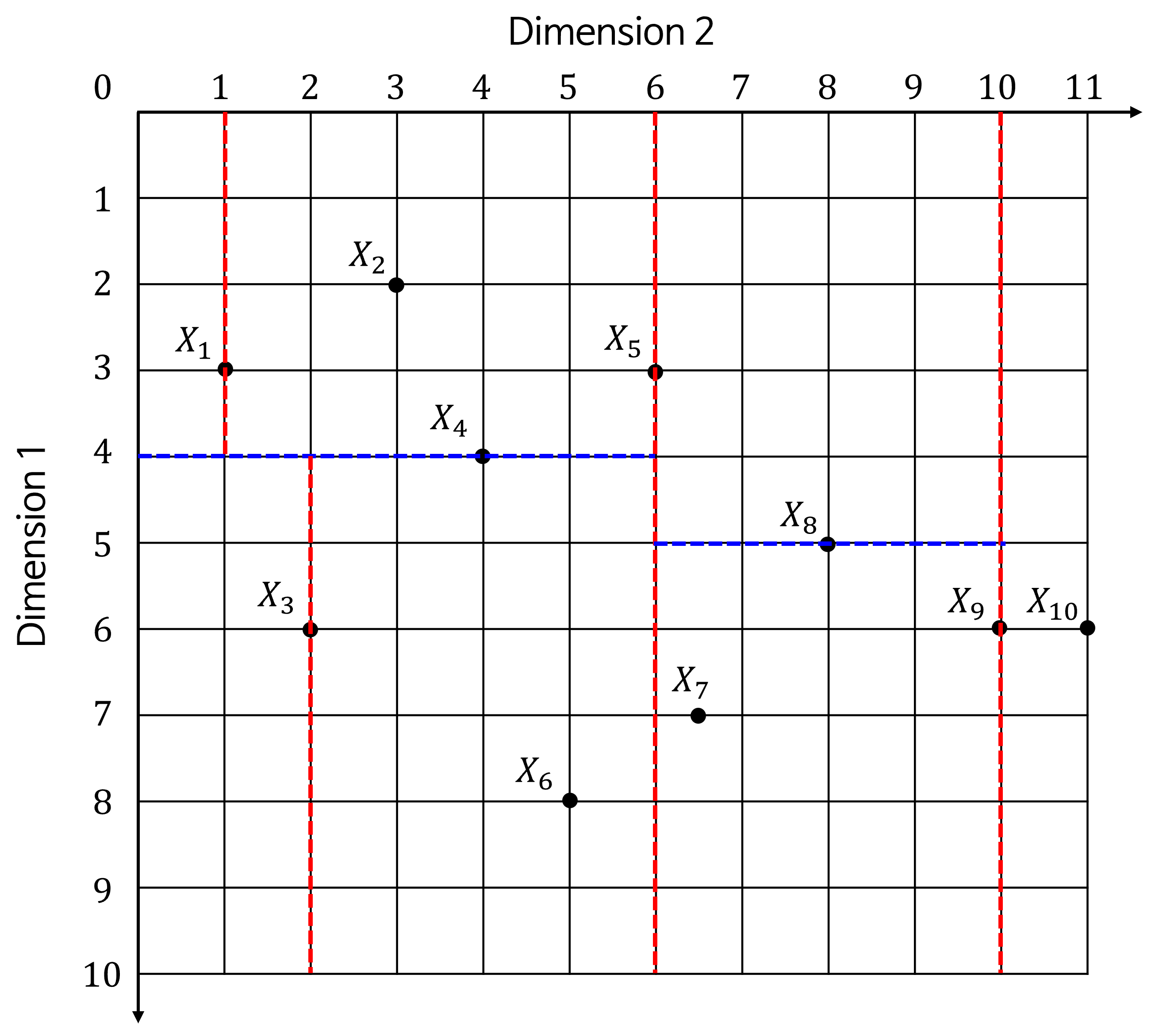
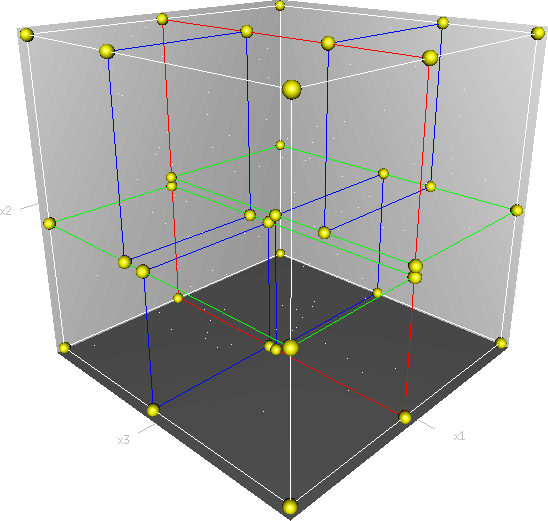
- 아래는 트리를 구성하면서 각 노드가 어떻게 공간을 분할하는 지 나타냅니다. 초록색 체크가 현재 선택된 노드로 공간을 분할하는 기준이 됩니다.
- 노란색 음영이 노드 기준으로
Left로 분류된 공간이고 초록색 음영이 노드 기준으로Right로 분류된 공간입니다.
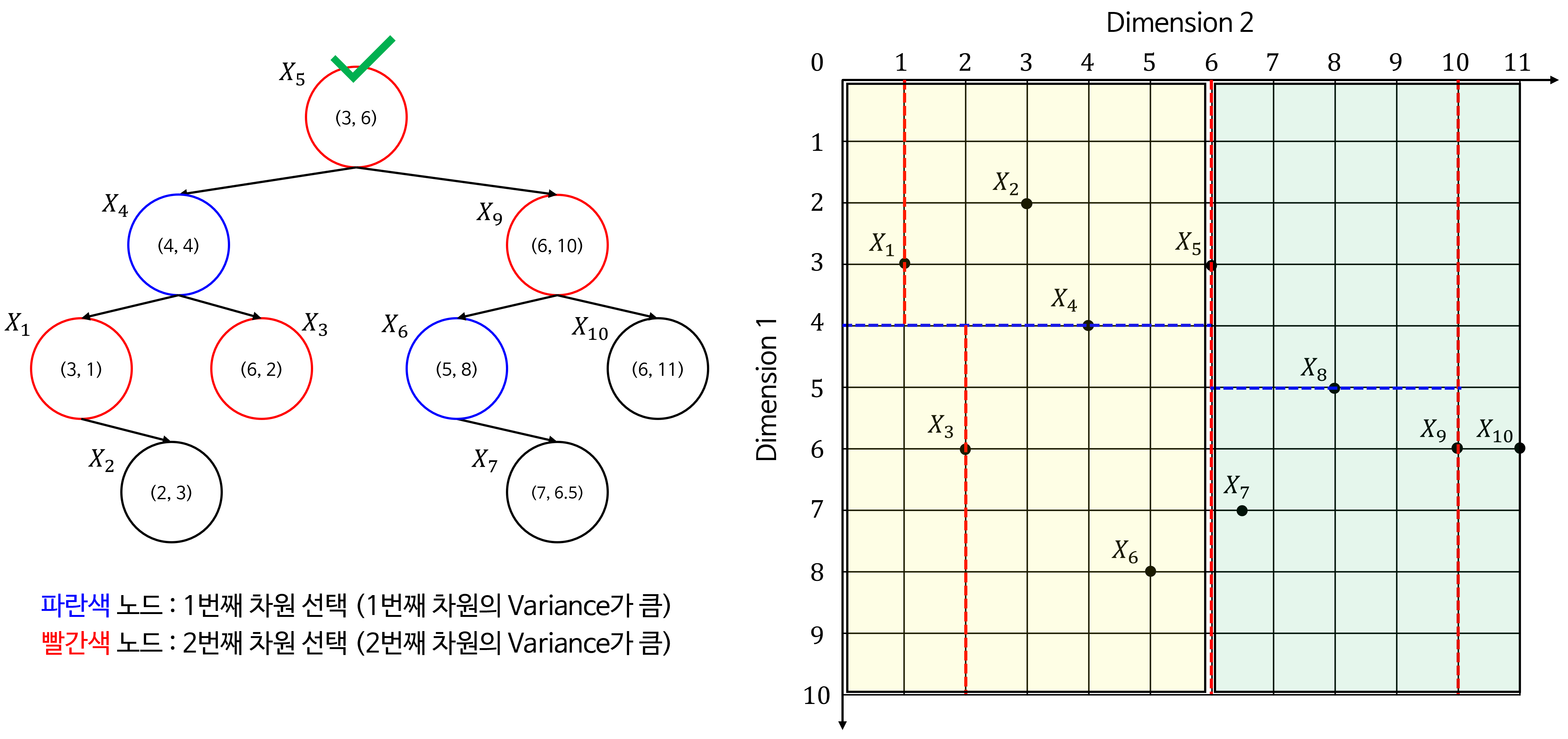
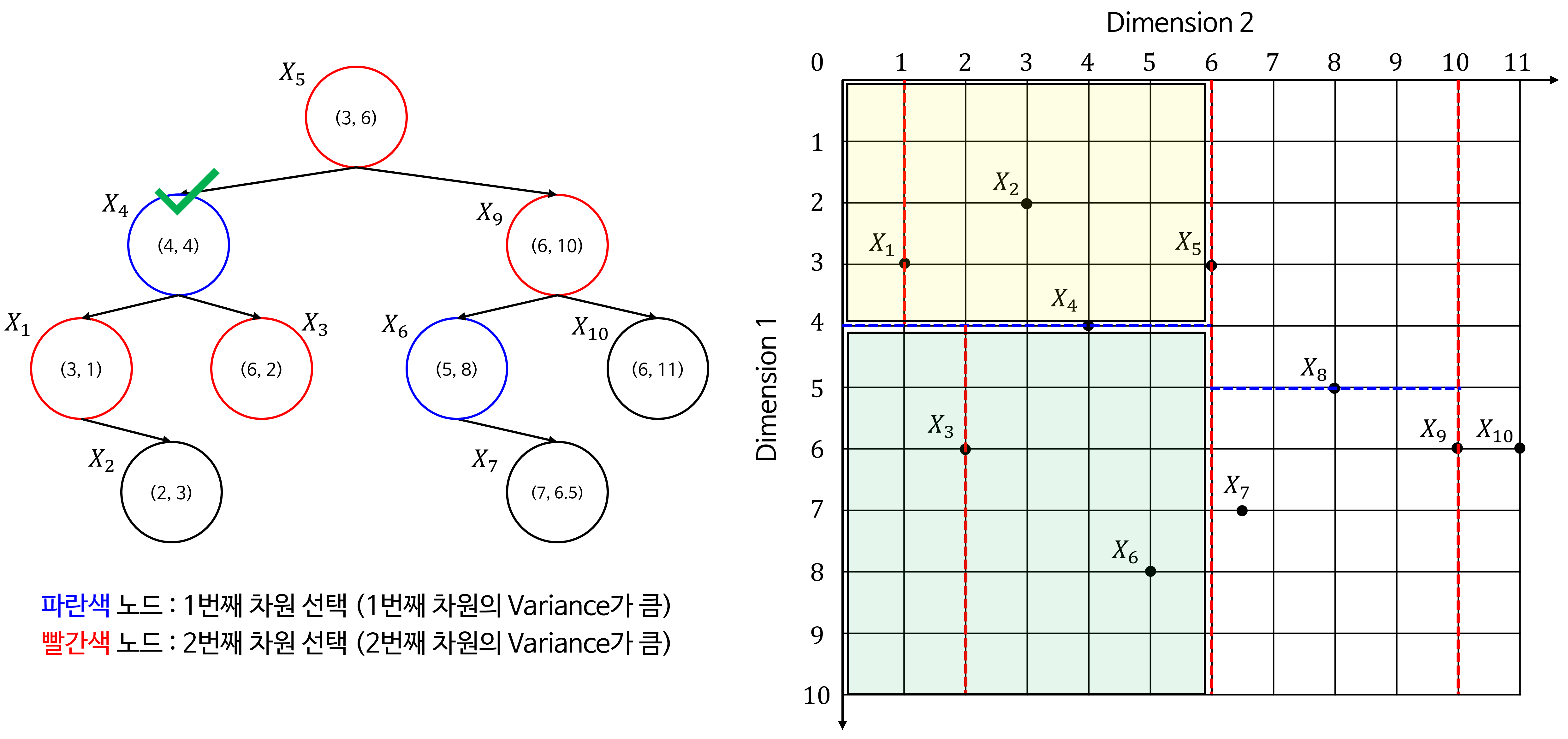
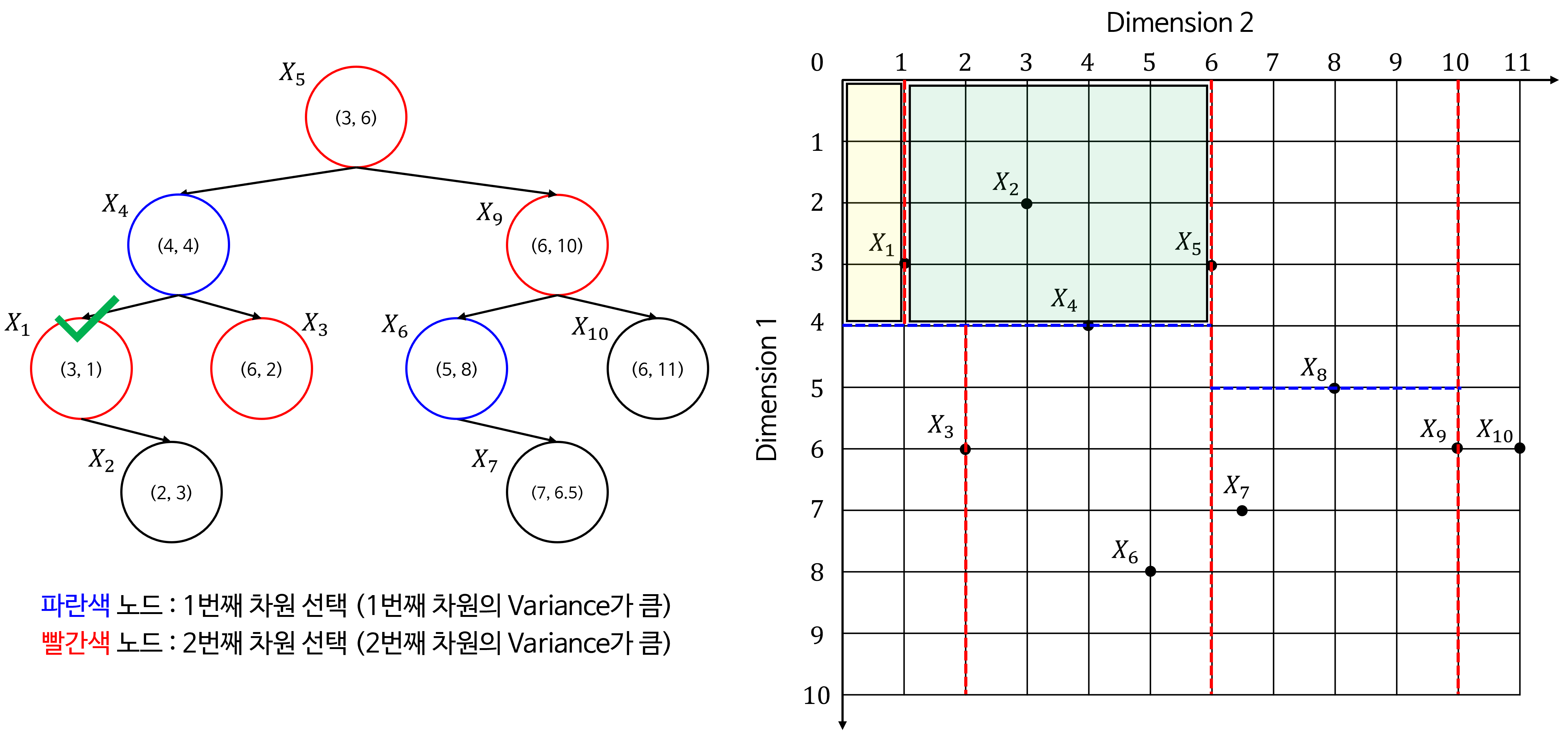
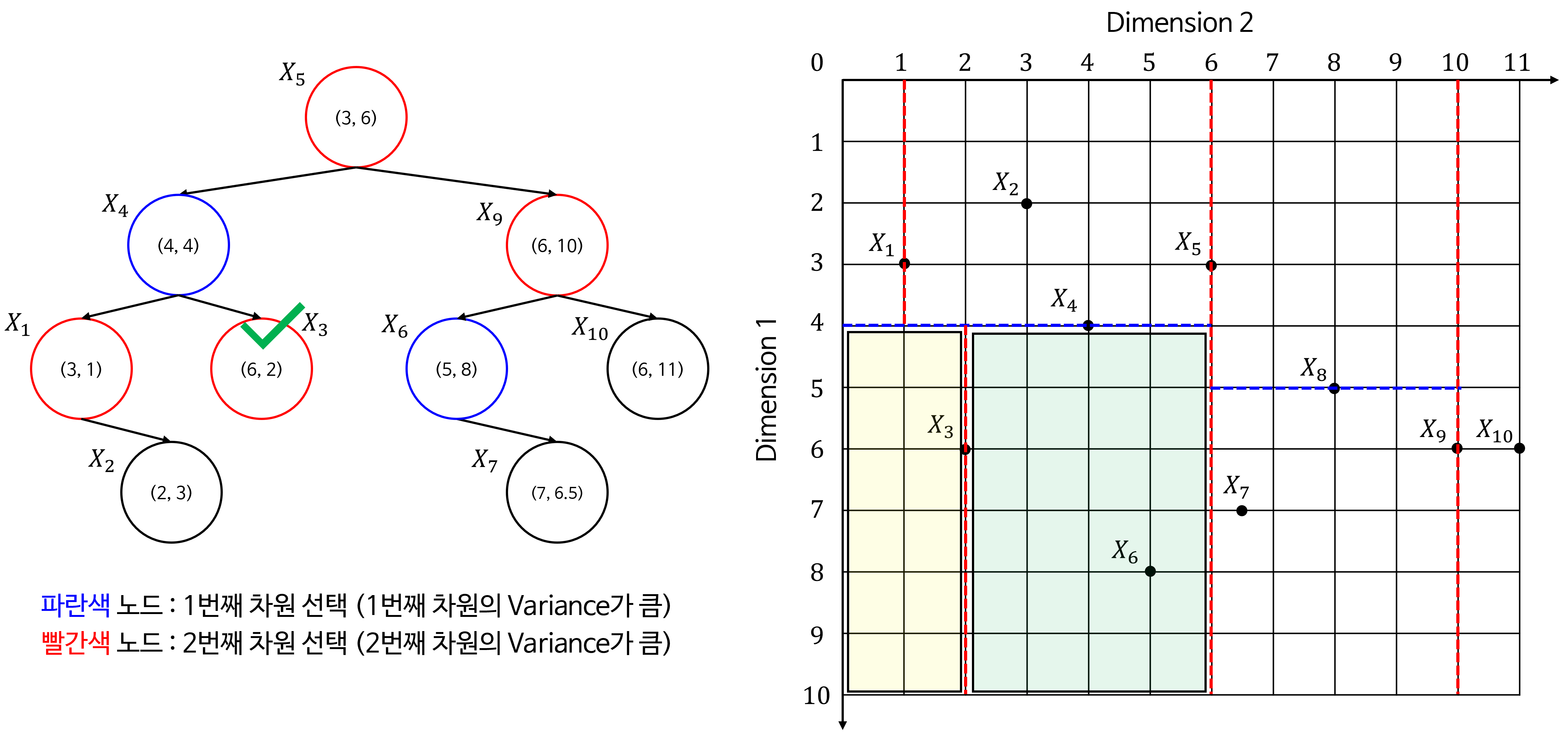
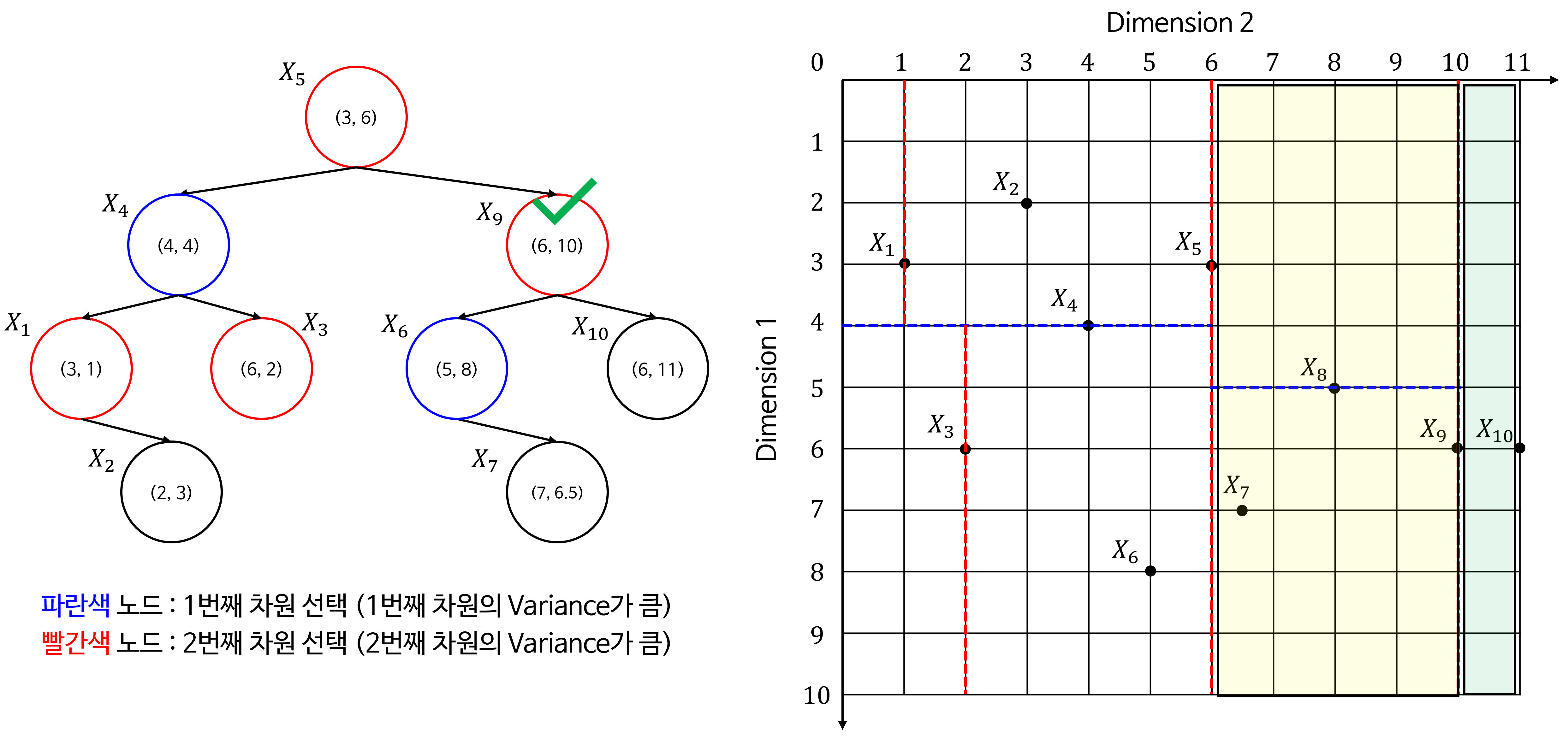
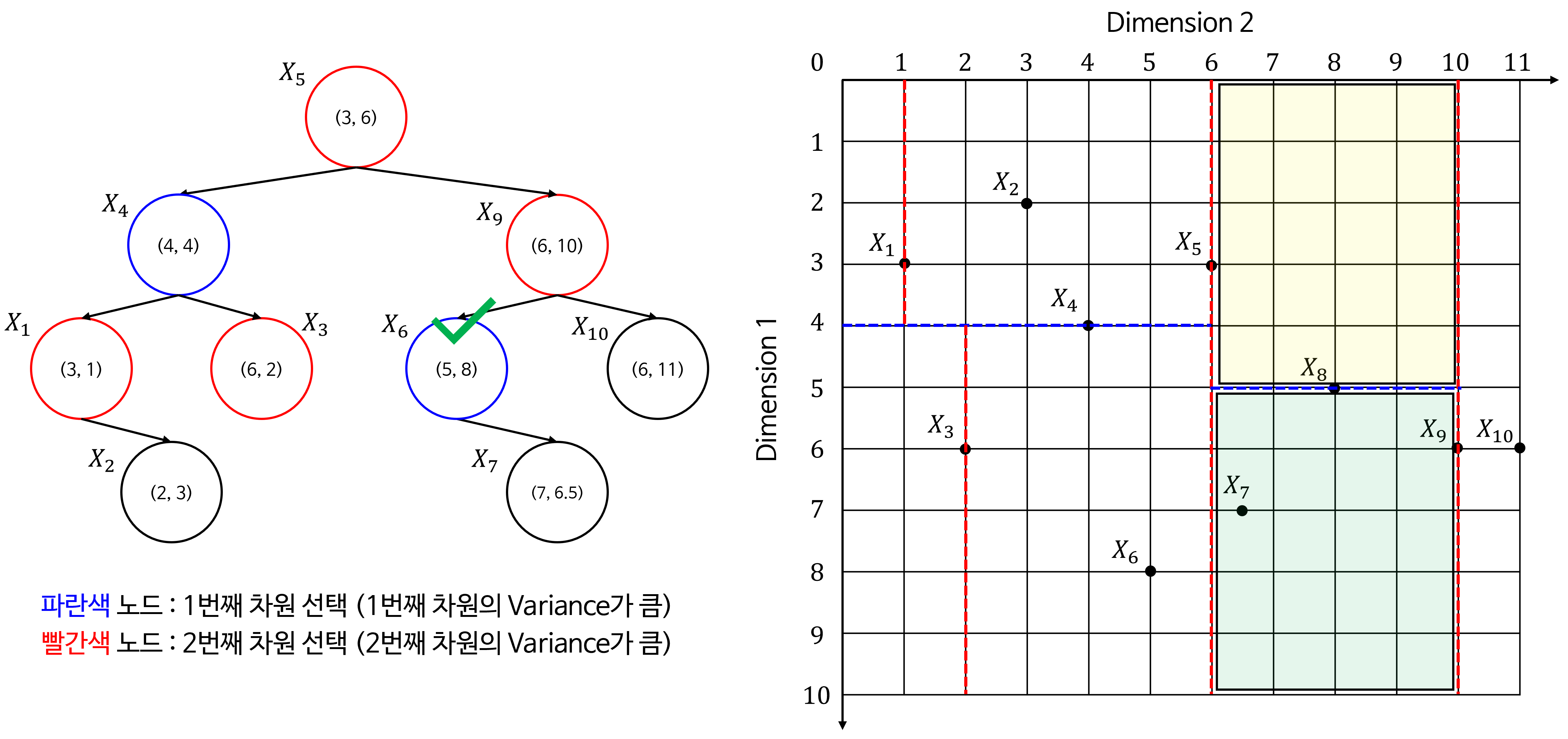
- 위 과정을 통해
KD-Tree가 어떻게 공간을 구분하여 트리를 생성하는 지 알 수 있습니다.