n차원 다각형의 넓이 계산 - gaussian37

n차원 다각형의 넓이 계산

출처 :
https://www.mathopenref.com/coordpolygonarea2.html
http://mathworld.wolfram.com/PolygonArea.html

이번 글에서는 n각형의 볼록 또는 오목 다각형의 좌표를 모두 알고 있을 때, n각형의 넓이 계산을 하는 방법에 대하여 알아보도록 하겠습니다.
이 내용은 중, 고등학교 과정에서 한번씩은 사용해 보았을 방법인데, 7차 교육 과정을 겪은 저 기준으로 교육 과정에는 없었지만 원리는 모른 체 편법으로 배웠었던 것 같습니다.
그러면 내용을 한번 알아보도록 하겠습니다.

목차

n각형의 넓이 계산 방법
원리 이해
한계 상황
c 코드

n각형의 넓이 계산 방법

먼저 계산하는 방법 부터 알아보도록 하겠습니다.
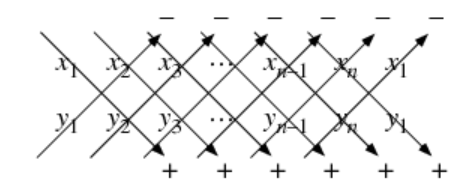
예를 들어 \((x_{1}, y_{1}) , (x_{2}, y_{2}), ... , (x_{n}, y_{n})\)의 n각형 꼭지점의 좌표가 있다고 한다면 넓이는 다음과 같습니다.
이 때, 좌표의 순서는 시계 반향이든, 반 시계 반향이든 연결된 형태로 이루어져 있어야 합니다.

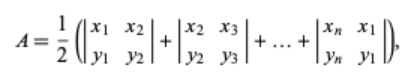
$Drawing$

여기서 \(\vert M \vert\) 는 determinant를 뜻하므로 풀어서 쓰면 다음과 같습니다.

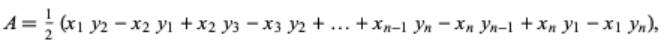
$Drawing$

이 식을 좀더 시각적으로 기억하기 좋게 표현하면 다음과 같습니다.

$Drawing$

즉, \((x_{1}, y_{1})\) 부터 \((x_{n}, y_{n})\) 까지 쓰고 마지막에 다시 한번 더 \((x_{1}, y_{1})\)을 쓴 다음에, 오른쪽 아래로 대각선 성분끼리 곱한 것은 더하고 오른쪽 위로 대각선 성분끼리 곱한 것을 뺀 다음에 2로 나누면 면적이 됩니다.

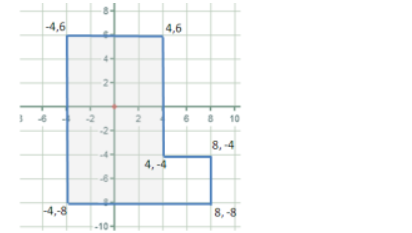
$Drawing$

위 그림에서 면적은 128이 됩니다. 그러면 이것을 위 식에 대입해서 한번 구해보겠습니다.

$Drawing$

위에서 설명한 방법대로 구하면 넓이를 구할 수 있음을 확인하였습니다.

원리 이해

쉬운 케이스

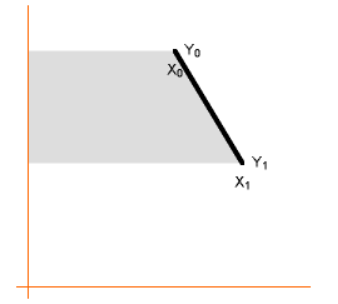
$Drawing$

두 점이 있을 때, 그 두 점을 연결한 선의 왼쪽 영역을 계속 더해나가는 것입니다.
위 그림을 기준으로 보면 0번째 점과 1번째 점을 연결한 선의 왼쪽 영역인 회색 구간을 전체 넓이에서 더하는 것입니다.

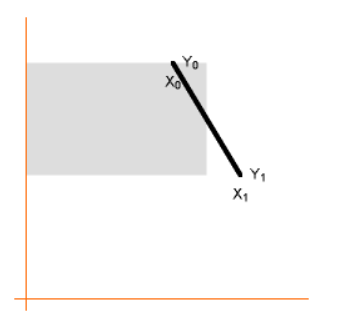
$Drawing$

여기서 x축의 부분만 생각을 조금 바꿔보겠습니다.
위 그림 같이 회색 영역을 바꿔도 넓이의 총합은 바뀌지 않습니다. 왜냐하면 새로 생긴 삼각형과 제거된 삼각형이 정확히 같기 때문입니다.
새로 생긴 삼각형 부분은 \(frac{1}{2} \times (x_{0} + x_{1}) \times (y_{0} - y_{1})\)로 구할 수 있습니다.
이렇게 변형된 직사각형 영역을 계속 더할 것입니다.

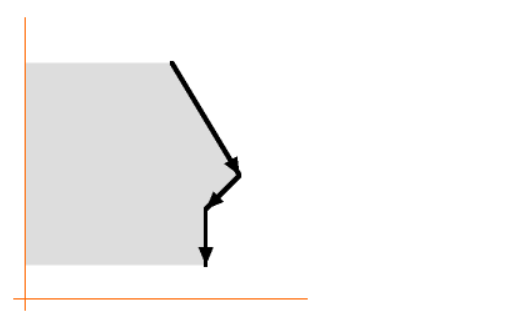
$Drawing$

여기 까지가 y좌표가 가장 아래 점인 점 까지 시계 방향으로 계속 더한 것이라고 가정하겠습니다.
그러면 이제 다각형을 완성하기 위해 점을 이어야 하므로 y좌표 기준으로 위로 올라가 보겠습니다.

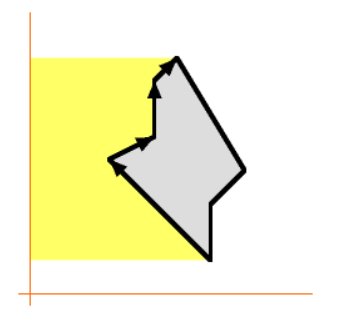
$Drawing$

앞에서 한 것과 똑같은 원리로 왼쪽 영역을 더해 갈 것입니다.
하지만 차이가 있다면 바로 곱해지는 \((y_{i} - y{i + 1})\)에 있습니다.
앞에서는 \(y\)의 값이 점점 줄어드는 방향으로 진행 되었기 때문에 \((y_{i} - y{i + 1})\)의 값이 양수 였습니다.
반면에 이번 스텝에서는 \((y_{i} - y{i + 1})\)의 값이 음수가 되어버립니다. 따라서 더해지는 영역이 음의 영역이 되어 자연스럽게 노란색 영역 만큼은 빼지게 됩니다.
사실 이러한 원리로 영역의 넓이를 계산하기 때문에, 연결된 점 순서로만 입력이 들어온다면 어느 지점에서 시작해도 상관 없습니다.

어려운 케이스

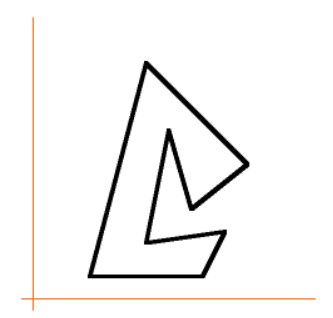
$Drawing$

앞에서 설명하였는데 볼록/오목 다각형에 이 방법이 모두 적용 가능하다고 하였습니다.
그러면 위와 같이 생긴 다각형도 적용이 되어야 하는데 어떻게 되는지 살펴보겠습니다. 결론적으로 말하면 영역이 더해졌다가 빼졌다가를 반복하면서 내부 영역만 최종적으로 남게 됩니다.

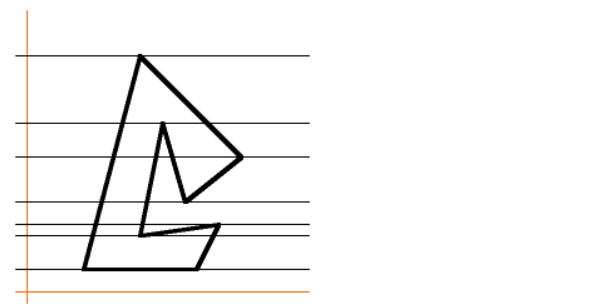
$Drawing$

영역의 변화를 살펴보기 위해 모든 꼭지점마다 수평선을 그어보겠습니다.

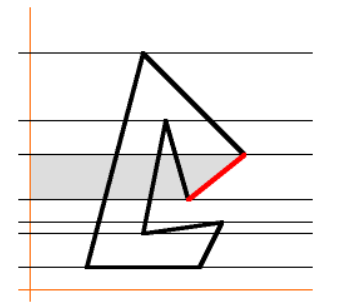
$Drawing$

앞의 쉬운 케이스와 같은 원리로 두 점을 연결한 선의 왼쪽 영역을 모두 더해보겠습니다. 그러면 위의 회색 영역만큼 모두 더해집니다.

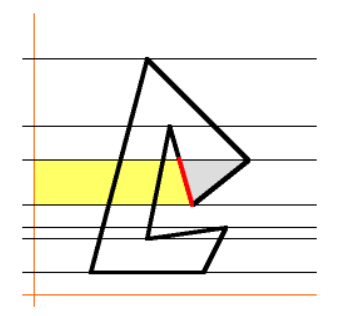
$Drawing$

그 다음 y값이 감소하는 방향으로 추가된 노란색 영역은 빼집니다. 따라서 회색 영역은 위 처럼 남게 됩니다.

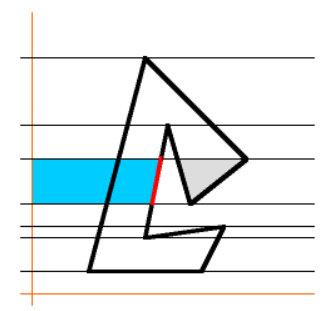
$Drawing$

그 다음 파란색 영역 만큼 다시 더해지게 됩니다.

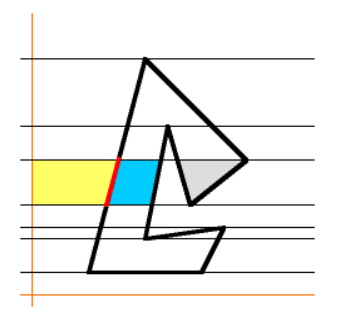
$Drawing$

다시 노란색 영역 만큼 빠지게 됩니다.

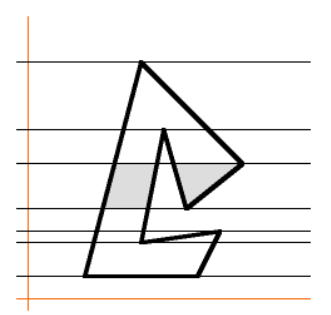
$Drawing$

최종적으로 회색 영역 만큼 남게 됩니다. 즉 다각형의 내부 영역 만큼만 정확하게 남게 됩니다.

한계 상황

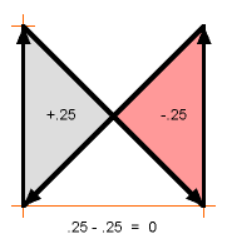
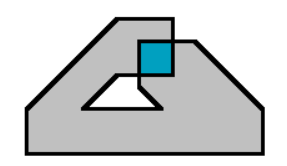
볼록/오목 다각형에서는 모두 사용할 수 있는 방법이지만 도형 내부에서 교차하는 영역이 발생하면 더해지고 빼지는 부분에서 중복이 발생하므로 영역을 구할 수 없습니다. 다음 그림을 참조하시기 바랍니다.

$Drawing$

$Drawing$

c 코드

아래 c코드에서 GetPolygonArea만 참조하시기 바랍니다.